Distribución exponencial

Distribución exponencial
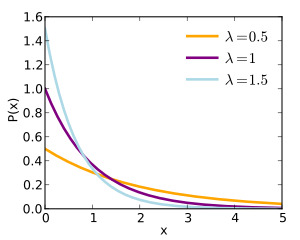
Función de densidad de probabilidad
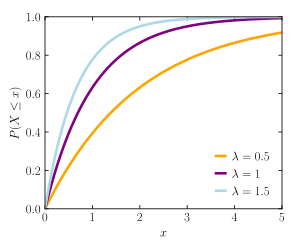
Función de distribución de probabilidad
Parámetros	$\lambda >0\,$
Dominio	$[0,\infty )\!$
Función de densidad (pdf)	$\lambda e^{-\lambda x}$
Función de distribución (cdf)	$1-e^{-\lambda x}$
Media	$1/\lambda \,$
Mediana	$\ln(2)/\lambda \,$
Moda	$0\,$
Varianza	$1/\lambda ^{2}\,$
Coeficiente de simetría	$2\,$
Curtosis	$9\,$
Entropía	$1-\ln(\lambda )\,$
Función generadora de momentos (mgf)	$\left(1-{\frac {t}{\lambda }}\right)^{-1}\,$
Función característica	$\left(1-{\frac {it}{\lambda }}\right)^{-1}\,$

En Teoría de Probabilidad y Estadística, la distribución exponencial es una distribución continua que se utiliza para modelar tiempos de espera para la ocurrencia de un cierto evento. Esta distribución al igual que la distribución geométrica tiene la propiedad de pérdida de memoria. La distribución exponencial es un caso particular de la distribución gamma.

Definición

Función de Densidad

Se dice que una variable aleatoria continua $X$ tiene una distribución exponencial con parámetro $\lambda >0$ y escribimos $X\sim \operatorname {Exp} (\lambda )$ si su función de densidad es

$f_{X}(x)=\lambda e^{-\lambda x}$

para $x\geq 0$.

Función de Distribución

Su función de distribución acumulada está dada por

$F_{X}(x)=1-e^{-\lambda x}$

para $x\geq 0$.

Parametrización Alternativa

La distribución exponencial en ocasiones se parametriza en términos del parámetro de escala $\beta =1/\lambda$ en cuya caso, la función de densidad será

$f_{X}(x)={\frac {1}{\beta }}\;e^{-{\frac {x}{\beta }}}$

para $x\geq 0$.

Función de Supervivencia

De forma adicional esta distribución presenta una función adicional que es función Supervivencia (S), que representa el complemento de la Función de distribución.

$S(x)=\operatorname {P} [X>x]=\left\{{\begin{matrix}1&{\text{para }}x<0\\e^{-\lambda x}&{\text{para }}x\geq 0\end{matrix}}\right.$

Propiedades

Si $X$ es una variable aleatoria tal que $X\sim \operatorname {Exp} (\lambda )$ entonces

La media de la variable aleatoria $X$ es

$\operatorname {E} [X]={\frac {1}{\lambda }}$

La varianza de la variable aleatoria $X$ es

$\operatorname {Var} [X]={\frac {1}{\lambda ^{2}}}$

El $n$-ésimo momento de la variable aleatoria $X$ es

$\operatorname {E} [X^{n}]={\frac {n!}{\lambda ^{n}}}$

La función generadora de momentos de $X$ para $\lambda >t$ está dada por

$M_{X}(t)=\left(1-{\frac {t}{\lambda }}\right)^{-1}={\frac {\lambda }{\lambda -t}}$

Escala

Si $X$ es una variable aleatoria tal que $X\sim \operatorname {Exp} (\lambda )$ y $c>0$ una constante entonces

$cX\sim \operatorname {Exp} \left({\frac {\lambda }{c}}\right)$

Pérdida de Memoria

Sea $X$ una variable aleatoria tal que $X\sim \operatorname {Exp} (\lambda )$ entonces para cualesquiera $x,y\geq 0$

$\operatorname {P} [X>x+y|X>y]=\operatorname {P} [X>x]$

Esto puede demostrarse fácilmente pues

${\begin{aligned}\operatorname {P} [X>x+y|X>y]&={\frac {\operatorname {P} [X>x+y\cap X>y]}{\operatorname {P} [X>y]}}\\&={\frac {\operatorname {P} [X>x+y]}{\operatorname {P} [X>y]}}\\&={\frac {e^{-\lambda (x+y)}}{e^{-\lambda y}}}\\&=e^{-\lambda x}\\&=\operatorname {P} [X>x]\end{aligned}}$

Cuantiles

La función cuantil (inversa de la función de distribución acumulada) para una variable aleatoria $X\sim \operatorname {Exp} (\lambda )$ está dada por

$F^{-1}(p)={\frac {-\ln(1-p)}{\lambda }}\qquad 0\leq p<1$

por lo que los cuantiles son:

El primer cuartil es

$F^{-1}\left({\frac {1}{4}}\right)=-{\frac {\ln \left({\frac {3}{4}}\right)}{\lambda }}={\frac {1}{\lambda }}\ln \left({\frac {4}{3}}\right)$

La mediana es

$F^{-1}\left({\frac {1}{2}}\right)=-{\frac {\ln \left({\frac {1}{2}}\right)}{\lambda }}={\frac {\ln(2)}{\lambda }}$

Y el tercer cuartil está dado por

$F^{-1}\left({\frac {3}{4}}\right)=-{\frac {\ln \left({\frac {1}{4}}\right)}{\lambda }}={\frac {\ln(4)}{\lambda }}$

Valor en riesgo condicional (pérdida esperada)

El valor condicional en riesgo (CVaR) también conocido como déficit esperado o supercuantil para Exp(λ) se obtiene de la siguiente manera:​

$${\begin{aligned}{\bar {q}}_{\alpha }(X)&={\frac {1}{1-\alpha }}\int _{\alpha }^{1}q_{p}(X)dp\\&={\frac {1}{(1-\alpha )}}\int _{\alpha }^{1}{\frac {-\ln(1-p)}{\lambda }}dp\\&={\frac {-1}{\lambda (1-\alpha )}}\int _{1-\alpha }^{0}-\ln(y)dy\\&={\frac {-1}{\lambda (1-\alpha )}}\int _{0}^{1-\alpha }\ln(y)dy\\&={\frac {-1}{\lambda (1-\alpha )}}[(1-\alpha )\ln(1-\alpha )-(1-\alpha )]\\&={\frac {-\ln(1-\alpha )+1}{\lambda }}\\\end{aligned}}$$

Probabilidad de superación amortiguada (bPOE)

La probabilidad amortiguada de superación es uno menos el nivel de probabilidad en el que el CVaR es igual al umbral $x$. Se obtiene de la siguiente manera:​

$${\begin{aligned}{\bar {p}}_{x}(X)&=\{1-\alpha |{\bar {q}}_{\alpha }(X)=x\}\\&=\{1-\alpha |{\frac {-\ln(1-\alpha )+1}{\lambda }}=x\}\\&=\{1-\alpha |\ln(1-\alpha )=1-\lambda x\}\\&=\{1-\alpha |e^{\ln(1-\alpha )}=e^{1-\lambda x}\}=\{1-\alpha |1-\alpha =e^{1-\lambda x}\}=e^{1-\lambda x}\end{aligned}}$$

Divergencia de Kullback-Leibler

La divergencia de Kullback-Leibler dirigida en nats de $e^{\lambda }$ (distribution de aproximación) de $e^{\lambda _{0}}$ (distribución "verdadera") viene dada por $${\begin{aligned}\Delta (\lambda _{0}\parallel \lambda )&=\mathbb {E} _{\lambda _{0}}\left(\log {\frac {p_{\lambda _{0}}(x)}{p_{\lambda }(x)}}\right)\\&=\mathbb {E} _{\lambda _{0}}\left(\log {\frac {\lambda _{0}e^{\lambda _{0}x}}{\lambda e^{\lambda x}}}\right)\\&=\log(\lambda _{0})-\log(\lambda )-(\lambda _{0}-\lambda )E_{\lambda _{0}}(x)\\&=\log(\lambda _{0})-\log(\lambda )+{\frac {\lambda }{\lambda _{0}}}-1.\end{aligned}}$$

Distribución de máxima entropía

Entre todas las distribuciones de probabilidad continuas con soporte cerrada-abierta 0, ∞ y media μ, la distribución exponencial con λ = 1/μ tiene la mayor entropía diferencial. En otras palabras, es la distribución de probabilidad de máxima entropía para una variante aleatoria X que es mayor o igual que cero y para la que E[X] es fija.​

Distribución del mínimo de variables aleatorias exponenciales

Sean X₁, ..., X_n variables aleatorias exponencialmente distribuidas con parámetros de tasa λ₁, ..., λ_n. Entonces $$\min \left\{X_{1},\dotsc ,X_{n}\right\}$$ también se distribuye exponencialmente, con el parámetro $$\lambda =\lambda _{1}+\dotsb +\lambda _{n}.$$

Esto puede verse considerando la función de distribución acumulativa complementaria:

$${\begin{aligned}&\Pr \left(\min\{X_{1},\dotsc ,X_{n}\}>x\right)\\={}&\Pr \left(X_{1}>x,\dotsc ,X_{n}>x\right)\\={}&\prod _{i=1}^{n}\Pr \left(X_{i}>x\right)\\={}&\prod _{i=1}^{n}\exp \left(-x\lambda _{i}\right)=\exp \left(-x\sum _{i=1}^{n}\lambda _{i}\right).\end{aligned}}$$

El índice de la variable que alcanza el mínimo se distribuye según la distribución categórica $$\Pr \left(X_{k}=\min\{X_{1},\dotsc ,X_{n}\}\right)={\frac {\lambda _{k}}{\lambda _{1}+\dotsb +\lambda _{n}}}.$$

Puede verse una prueba dejando que $I=\operatorname {argmin} _{i\in \{1,\dotsb ,n\}}\{X_{1},\dotsc ,X_{n}\}$. Entonces, $${\begin{aligned}\Pr(I=k)&=\int _{0}^{\infty }\Pr(X_{k}=x)\Pr(\forall _{i\neq k}X_{i}>x)\,dx\\&=\int _{0}^{\infty }\lambda _{k}e^{-\lambda _{k}x}\left(\prod _{i=1,i\neq k}^{n}e^{-\lambda _{i}x}\right)dx\\&=\lambda _{k}\int _{0}^{\infty }e^{-\left(\lambda _{1}+\dotsb +\lambda _{n}\right)x}dx\\&={\frac {\lambda _{k}}{\lambda _{1}+\dotsb +\lambda _{n}}}.\end{aligned}}$$

Nótese que $$\max\{X_{1},\dotsc ,X_{n}\}$$

$$\max\{X_{1},\dotsc ,X_{n}\}$$ no es una distribución exponencial, si X₁, …, X_n no todos tienen parámetro 0.​

Momentos conjuntos de estadísticos de orden exponencial i.i.d

Sean $X_{1},\dotsc ,X_{n}$ $n$ independent and identically distributed variables aleatorias exponenciales con parámetro de tasa λ. Sean $X_{(1)},\dotsc ,X_{(n)}$ los correspondientes estadísticos de orden. Para $i<j$ , el momento conjunto $\operatorname {E} \left[X_{(i)}X_{(j)}\right]$ de los estadísticos de orden $X_{(i)}$ y $X_{(j)}$ viene dado por

$${\begin{aligned}\operatorname {E} \left[X_{(i)}X_{(j)}\right]&=\sum _{k=0}^{j-1}{\frac {1}{(n-k)\lambda }}\operatorname {E} \left[X_{(i)}\right]+\operatorname {E} \left[X_{(i)}^{2}\right]\\&=\sum _{k=0}^{j-1}{\frac {1}{(n-k)\lambda }}\sum _{k=0}^{i-1}{\frac {1}{(n-k)\lambda }}+\sum _{k=0}^{i-1}{\frac {1}{((n-k)\lambda )^{2}}}+\left(\sum _{k=0}^{i-1}{\frac {1}{(n-k)\lambda }}\right)^{2}.\end{aligned}}$$ Esto puede verse invocando la ley de la expectativa total y la propiedad sin memoria: $${\begin{aligned}\operatorname {E} \left[X_{(i)}X_{(j)}\right]&=\int _{0}^{\infty }\operatorname {E} \left[X_{(i)}X_{(j)}\mid X_{(i)}=x\right]f_{X_{(i)}}(x)\,dx\\&=\int _{x=0}^{\infty }x\operatorname {E} \left[X_{(j)}\mid X_{(j)}\geq x\right]f_{X_{(i)}}(x)\,dx&&\left({\textrm {since}}~X_{(i)}=x\implies X_{(j)}\geq x\right)\\&=\int _{x=0}^{\infty }x\left[\operatorname {E} \left[X_{(j)}\right]+x\right]f_{X_{(i)}}(x)\,dx&&\left({\text{by the memoryless property}}\right)\\&=\sum _{k=0}^{j-1}{\frac {1}{(n-k)\lambda }}\operatorname {E} \left[X_{(i)}\right]+\operatorname {E} \left[X_{(i)}^{2}\right].\end{aligned}}$$

La primera ecuación se sigue de la ley de la expectativa total. La segunda ecuación explota el hecho de que una vez que condicionamos en $X_{(i)}=x$, debe seguirse que $X_{(j)}\geq x$. La tercera ecuación se basa en la propiedad sin memoria para reemplazar $\operatorname {E} \left[X_{(j)}\mid X_{(j)}\geq x\right]$ con $\operatorname {E} \left[X_{(j)}\right]+x$.

Ejemplo

Ejemplos para la distribución exponencial es la distribución de la longitud de los intervalos de una variable continua que transcurren entre dos sucesos, que se distribuyen según la distribución de Poisson.

• El tiempo transcurrido en un centro de llamadas hasta recibir la primera llamada del día se podría modelar como una exponencial.
• El intervalo de tiempo entre terremotos (de una determinada magnitud) sigue una distribución exponencial.
• Supongamos una máquina que produce hilo de alambre, la cantidad de metros de alambre hasta encontrar una falla en el alambre se podría modelar como una exponencial.
• En fiabilidad de sistemas, un dispositivo con tasa de fallo constante sigue una distribución exponencial.

Distribuciones Relacionadas

• Si $X\sim \operatorname {Laplace} (\mu ,\beta ^{-1})$ entonces $|X-\mu |\sim \operatorname {Exp} (\beta )$.
• Si $X\sim \operatorname {Pareto} (1,\lambda )$ entonces $\ln(X)\sim \operatorname {Exp} (\lambda )$.
• Si $X\sim \Gamma (1,\lambda )$ entonces $X\sim \operatorname {Exp} (\lambda )$.
• Si $X_{1},X_{2},\dots ,X_{n}$ son variables aleatorias independientes tales que $X_{i}\sim \operatorname {Exp} (\lambda )$entonces $\sum \limits _{i=1}^{n}X_{i}\sim \Gamma \left(n,\lambda \right)$, donde $\Gamma \left(n,\lambda \right)$ es la distribución de Erlang con parámetros $n\in \mathbb {N}$ y $\lambda$, esto es $\sum \limits _{i=1}^{n}X_{i}\sim \operatorname {Erlang} \left(n,\lambda \right)$. 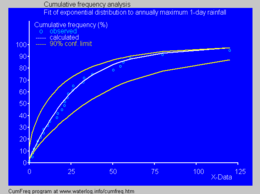Es decir, la suma de $n$ variables aleatorias independientes con distribución exponencial con parámetro $\lambda$ es una variable aleatoria con distribución de Erlang.

Distribución cumulativa ajustada a máximos anuales de lluvias diarias​

Inferencia Estadística

Suponga que $X$ es una variable aleatoria tal que $X\sim \operatorname {Exp} (\lambda )$ y $x_{1},x_{2},\dots ,x_{n}$ es una muestra proveniente de $X$.

Estimación de Parámetros

El estimador por máxima verosimilitud de $\lambda$ se construye como sigue:

La función de verosimilitud está dada por

${\begin{aligned}{\mathcal {L}}(\lambda )&=\prod _{i=1}^{n}\lambda e^{-\lambda x_{i}}\\&=\lambda ^{n}\operatorname {exp} \left(-\lambda \sum _{i=1}^{n}x_{i}\right)\\&=\lambda ^{n}\operatorname {exp} (-\lambda n{\bar {x}})\end{aligned}}$

donde

${\bar {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}$

es la media muestral.

Tomando logaritmos a la función de verosimilitud

${\begin{aligned}\ln {\mathcal {L}}(\lambda )&=\ln \left(\lambda ^{n}\operatorname {exp} (-\lambda n{\bar {x}})\right)\\&=n\ln \lambda -\lambda n{\bar {x}}\end{aligned}}$

derivando respecto a $\lambda$ obtenemos

${\begin{aligned}{\frac {d\ln {\mathcal {L}}}{d\lambda }}&={\frac {d}{d\lambda }}(n\ln \lambda -\lambda n{\bar {x}})\\&={\frac {n}{\lambda }}-n{\bar {x}}\end{aligned}}$

Si igualamos a $0$ obtenemos el estimador ${\hat {\lambda }}$ dado por

${\hat {\lambda }}={\frac {1}{\bar {x}}}$

El estimador ${\hat {\lambda }}$ es un estimador NO insesgado pues

$\operatorname {E} [{\hat {\lambda }}]\neq \lambda$

Aplicación

En la hidrología, la distribución exponencial se emplea para analizar variables aleatorias extremos de variables como máximos mensuales y anuales de la precipitación diaria.​

• La imagen azul ilustra un ejemplo de ajuste de la distribución exponencial a lluvias máximas diárias anuales ordenadas, mostrando también la franja de 90% de confianza, basada en la distribución binomial. Las observaciones presentan los marcadores de posición, como parte del análisis de frecuencia acumulada.

Métodos computacionales

Generador de números pseudoaleatorios

Para obtener números pseudoaleatorios la variable aleatoria $X$ con distribución exponencial y parámetro $\lambda$, se utiliza un algoritmo basado en el método de la transformada inversa.

Para generar un valor de $X\sim \operatorname {Exp} (\lambda )$ a partir de una variable aleatoria $U\sim \operatorname {U} (0,1)$ se utiliza el siguiente algoritmo

$X=-{\frac {1}{\lambda }}\ln(1-U)$

utilizando el hecho de que si $U\sim \operatorname {U} (0,1)$ entonces $1-U\sim \operatorname {U} (0,1)$ por lo que una versión más eficiente del algoritmo es

$X=-{\frac {1}{\lambda }}\ln(U)$

Véase también

• Proceso de Poisson
• Distribución Gamma
• Distribución de Erlang
• Distribución χ²
• Distribución Poisson

Software

Se puede usar software y un programa de computadora para el ajuste de una distribución de probabilidad, incluyendo la exponencial, a una serie de datos:

• Easy fit Archivado el 23 de febrero de 2018 en Wayback Machine., "data analysis & simulation"
• MathWorks Benelux (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última).
• ModelRisk, "risk modelling software"
• Ricci distributions, fitting distrubutions with R , Vito Ricci, 2005
• Risksolver, automatically fit distributions and parameters to samples
• StatSoft distribution fitting Archivado el 30 de agosto de 2012 en Wayback Machine.
• CumFreq [2] , libre sin costo, incluye intervalos de confianza a base de la distribución binomial

Enlaces externos

• Calculadora Distribución exponencial
• [http://cajael.com/mestadisticos/T7DContinuas/node20.php (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última).] Calcular la probabilidad de una distribución exponencial con R (lenguaje de programación)

• Datos: Q237193
• Multimedia: Exponential distribution / Q237193