Kaardiprojektsioon
Kaardiprojektsioon ehk kartograafiline projektsioon on sfäärilise pinna tasapinnal kujutamise matemaatiline viis.
Kaardiprojektsioonide liigitamine
[muuda | muuda lähteteksti]Projektsioone liigitatakse mitme erineva printsiibi järgi. Seda on tehtud projektsiooni omaduse (moonutuse), aspekti, regionaalse sobivuse (näiteks poolkerade, maailmajagude jne) järgi. Kõige enam on liigitamisel lähtutud projektsioonide siirdepinnast ning seda kirjeldavast paralleelide ja meridiaanide üldkujust.

Kaardiprojektsiooni klassid
[muuda | muuda lähteteksti]Kaardiprojektsioonide klasse eristatakse kolme peamiselt kasutatava siirdepinna – tasandi, silindri ja koonuse – alusel. Paralleelide ja meridiaanide kuju ehk kaardivõrk nende kolme põhiklassi normaalaspekti puhul (normaalvõrk) on iseloomulik ja hästi äratuntav – meridiaanid kujutuvad nende puhul alati sirgetena ning paralleelid sirgetena või kontsentriliste ringjoontena. Normaalvõrgu sarnasuse alusel põhiklassidega on moodustatud pseudoklassid. Pseudoklasside projektsioonid on saadud reeglina põhiklasside modifitseerimise teel ja säilitavad normaalaspekti korral paralleelide kuju. Lisaks eristatakse kooniliste ja pseudokooniliste projektsioonide kõrval ka polükooniliste projektsioonide klass. Kuna suur hulk projektsioone ei ole viidavad eelpoolnimetatud klasside alla, siis lisandub kaardiprojektsiooniklasside nimistusse alati ka kokkuleppeliste projektsioonide klass:
- silindrilised projektsioonid
- pseudosilindrilised projektsioonid
- koonilised projektsioonid
- pseudokoonilised projektsioonid
- polükoonilised projektsioonid
- tasandilised e asimutaalsed projektsioonid
- pseudotasandilised projektsioonid
- kokkuleppelised e muud projektsioonid
Kaardiprojektsiooni aspektid[2]
[muuda | muuda lähteteksti]
Kaardiprojektsiooni aspekte on kolm: normaal-, põik- ja kaldaspekt. Ühel projektsioonil võib olla mitu aspekti ning kuna matemaatiliselt on arvutuseeskirjad iga aspekti jaoks erinevad, loetakse neid erinevateks projektsioonideks. Samas on projektsiooni konstrueerimise põhimõtted üldreeglina samad, muutuvad standardjoonte suunad, kuid projektsiooni põhiomadused reeglina säilivad.
Normaalaspekti puhul on abipind või standardjoone tasand maaellipsoidi teljega risti. Silindrilistel projektsioonidel tähendab see projektsiooni konstrueerimist ekvaatori suhtes (vt kõrvalolevat joonist), koonilistel projektsioonidel standardparalleeli suhtes ja asimutaalsetel projektsioonidel Maa pooluse suhtes.
Põikaspekti puhul on projektsiooni standardjooned ehk abipind normaalaspektiga võrreldes risti. Silindrilistel projektsioonidel on konstrueerimise aluseks meridiaan (vt kõrvalolevat joonist), koonilistel projektsioonidel ekvaatoriga ristuv(ad) väikeringjoone kaar(ed) ning asimutaalsetel projektsioonidel paikneb tasandi puutepunkt või projektsioonikese ekvaatoril.
Kaldaspekti puhul on projektsiooni standardjooned orienteeritud mingis muus suunas kui normaal- või põikaspekti puhul.
Kaardi projitseerimisviisid[3]
[muuda | muuda lähteteksti]

Tüüpilisemad kaardi projitseerimisviisid on:
- ortogonaalne projektsioon – projitseeritakse tasapinnale paralleelsete sirgete abil. See tähendab, et iga punkti jaoks Maal leitakse lähim punkt tasapinnal. Näiteks foto planeedist Maa, mis on tehtud piisavalt kaugelt (näiteks Kuult), on ortogonaalne projektsioon Maast. Praktikas leiab ortogonaalne projektsioon kasutamist topograafiliste plaanide puhul. Väikesemõõtkavaliste kaartide korral võimaldab see viis pindalamoonutusi hoida minimaalsetena.
- tsentraalne (gnoomiline) projektsioon – projitseerimiskese asub maaellipsoidi keskmes. Lihtne geomeetriline lahendus, mille oluline omadus on see, et mitmetel selle projektsiooniga kaartidel kujutatakse kõige lühemad jooned kahe punkti vahel sirgjoontena.
- stereograafiline projektsioon – projitseerimiskese asub maaellipsoidi vastasküljel. Tegu on klassikalise projitseerimisviisiga, mis tasandilise siirdepinna korral annab õigenurkse kaardi.
- perspektiivne projektsioon – projitseerimiskese asub mis tahes punktis väljaspool maaellipsoidi. Perspektiivse projektsiooniga kaartidel on võimalik kujutada Maad, nagu see näib lennult vaadatuna. Näiteks on perspektiivse projektsiooniga kosmoses tehtud fotod Maast.
Moonutused kaardil[4]
[muuda | muuda lähteteksti]
Mitte ükski kaardiprojektsioon ei kujuta Maa pinda täpselt sellisena, nagu see on. Kõikide kaardiprojektsioonide puhul esineb kaardimoonutusi. Kaardiprojektsioon valitakse vastavalt kaardi kasutuseesmärgile, st ühe projektsiooniga kaasnevad moonutused kaardil on mingis kindlas olukorras vastuvõetavamad kui teisega kaasnevad moonutused. Kaardiprojektsioone on piiramatul hulgal[5]. Üks ja sama kujund maaellipsoidil annab nelja klassikalise projitseerimisviisi korral tasapinnale erinevaid tulemusi.
Kartograafias vaadeldakse olulisemate moonutustena:
- joonpikkuste moonutust
- pindalade moonutust
- nurkade moonutust
- kuju moonutust
Reeglina moonutuste suurus kaardipinna eri osades muutub. Kui joonpikkuste moonutus esineb igal kaardil, siis ka kaardi mõõtkava muutub kaardi erinevates osades. Kõik moonutuste liigid on ühel kaardil omavahel väga kindlates matemaatilistes seostes ehk ühe muutmine mõjutab ka teisi.
Kaardiprojektsioonide väljatöötamise ja kasutamise kõige olulisem küsimus seisneb just moonutuste jaotumises kaardipinnal. Sageli on eesmärgiks konstrueerida projektsioon, mille puhul kas teatud liiki moonutus puudub või see püsib etteantud piirides.
Projektsiooni omadused[6]
[muuda | muuda lähteteksti]Moonutuste iseloomu alusel räägitakse projektsiooni omadustest. Enamasti rühmitatakse projektsioonid omaduste järgi konformseteks, õigenurkseteks, õigepindseteks (ekvivalentsed), õigepikkuselisteks, vähimmoondelisteks ja sobedateks.
Konformseks nimetatakse projektsiooni, mille puhul kaardi suvalisest punktist võetuna jääb mõõtkava igas suvalises suunas võrdseks. See tähendab, et lõpmatult väike geomeetriline kujund kaardil ei deformeeru (ringjoon jääb ringjooneks). Sellist omadust nimetatakse konformsuseks ehk kuju moondevaba edasiandmiseks. Konformsed projektsioonid on ühtlasi ka õigenurksed.
Õigenurkse projektsiooniga kaardil vastab nurk kahe suvalise suuna vahel tegelikkusele. Tegelikkuses mõeldakse "suuna" all kindla asimuudiga joont ehk loksodroomi, mis pole looduses pikkade vahemaade korral sirgjoon. Lühim, sirgjooneline lõik looduses kahe punkti vahel on ortodroom, mis muudab oma asimuuti ega pruugi kujutuda õigenurksel kaardil sirgena. Õigenurkse projektsiooni korral meridiaanid ja paralleelid ristuvad. Õigenurksed konformsed projektsioonid on kõige levinumad suuremõõtkavaliste topograafiliste kaartide alusprojektsioonina, samuti on need laialt kasutatavad navigatsioonikaartide ja erikaartide (merendus, lennundus, raadiolokatsioon jms) puhul, kus suundade võtmine ja nurkade mõõtmine on kaardi juures kõige olulisem.
Õigepindse (ekvivalentse) projektsiooni korral säilib kogu kaardi ulatuses suvaliste alade omavaheline pindalaline proportsioon. Üldreeglina tähendab õigepindsus ilmselget nurkade moonutamist, sellega kaasneb ka erimõõtkava muutumine sõltuvalt suunast. Õigepindsed projektsioonid on vajalikud selliste väikesemõõtkavaliste kaartide jaoks, kus pindalafaktori arvestamine on oluline. Tungivalt on soovitav selliste projektsioonide kasutamine teemakaartide juures, mis esitavad teavet tihedusele tuginedes (nt rahvastikutiheduse kaardid). Õigepindseid projektsioone on suurel hulgal ja neid kasutatakse palju atlasekaartide puhul.
Õigepikkuselise (ekvidistantse) projektsiooni puhul on teatud jooned (tavaliselt kaugus projektsiooni keskmest) moonutusteta. See kehtib ainult ühest-kahest punktist võetuna ja/või kindlatel joontel, milleks tavaliselt võivad olla meridiaanid, paralleelid. Pikkused muude punktide vahel on aga mingil määral moonutatud. Õigepikkuselisi projektsioone kasutatakse erikaartide puhul (nt raadiolokatsioonis) või ka mujal, kus soovitakse näidata tegelikke kaugusi mingist punktist.
Vähimmoondelise projektsiooni puhul on, nagu nimetuski ütleb, tegu projektsiooniga, millel on taotluslikult püütud viia kõik põhilised moonutused miinimumini. Sellised projektsioonid omavad praktilist tähtsust väikesemõõtkavaliste, ent tehnilisema otstarbega kaartide või ka teatmekaartide puhul.
Sobedad on üldnimetus projektsioonide kohta, mis ei ole ei konformsed ega ka õigepindsed (kuid võivad olla õigepikkuselised). Neid nimetatakse ka kokkuleppelisteks ehk konventsionaalseteks projektsioonideks. Peamist rakendust leiavad sobedad projektsioonid atlasekaartide juures, mis sageli püüavad parandada mingite konformsete või õigepindsete projektsioonide nõrku külgi, esile tuua üht või teist ideed (nt Maa sfäärilisus, mandrite paiknemine jms) või teatud proportsioonide hoidmist (nt maismaa ja maailmamere vahel).
Väga suurte moonutustega ehk ekstravagantseid kindlate omadusteta projektsioone nimetatakse suvalisteks ehk meelevaldseteks projektsioonideks.
Kaardiprojektsioonide nimetamise reeglid
[muuda | muuda lähteteksti]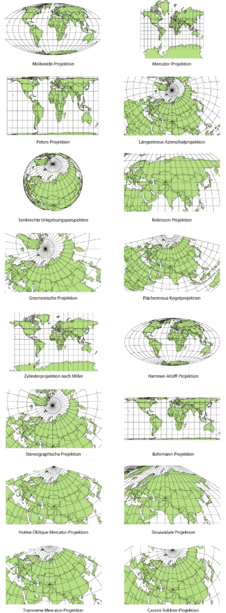 On olemas palju erinevaid kaardiprojektsioone. Konkreetse kaardiprojektsiooni nimetuses kasutatakse sõna "projektsioon" ees pärisnime (projektsiooni autori perekonnanimi) omastavas käändes ja sõnu, mis väljendavad selle projektsiooni iseloomulikku tunnust, omadust, klassi, aspekti või vormilist tunnust. Võidakse kasutada mitut täiendit, kuid enamasti kasutatakse ainult pärisnime (näiteks Robinsoni projektsioon). Vajadus täiendavate tunnuste sissetoomiseks tekib näiteks siis, kui üks inimene on loonud mitu erinevat projektsiooni (näiteks Lamberti konformne kooniline projektsioon ja Lamberti õigepindne silindriline projektsioon). See reegel pole siiski universaalne, sest on olemas Mercatori projektsioon, mille nimes ei sisaldu täiendeid, ehkki on olemas ka Mercatori põikprojektsioon, Mercatori universaalne põikprojektsioon ja Mercatori kaldprojektsioon. Seega on projektsioonide nimed võimaluse korral lihtsad ja lühikesed. Projektsioonide nimedes sisalduvad täiendavad omadused esitatakse alljärgnevas järjestuses:
On olemas palju erinevaid kaardiprojektsioone. Konkreetse kaardiprojektsiooni nimetuses kasutatakse sõna "projektsioon" ees pärisnime (projektsiooni autori perekonnanimi) omastavas käändes ja sõnu, mis väljendavad selle projektsiooni iseloomulikku tunnust, omadust, klassi, aspekti või vormilist tunnust. Võidakse kasutada mitut täiendit, kuid enamasti kasutatakse ainult pärisnime (näiteks Robinsoni projektsioon). Vajadus täiendavate tunnuste sissetoomiseks tekib näiteks siis, kui üks inimene on loonud mitu erinevat projektsiooni (näiteks Lamberti konformne kooniline projektsioon ja Lamberti õigepindne silindriline projektsioon). See reegel pole siiski universaalne, sest on olemas Mercatori projektsioon, mille nimes ei sisaldu täiendeid, ehkki on olemas ka Mercatori põikprojektsioon, Mercatori universaalne põikprojektsioon ja Mercatori kaldprojektsioon. Seega on projektsioonide nimed võimaluse korral lihtsad ja lühikesed. Projektsioonide nimedes sisalduvad täiendavad omadused esitatakse alljärgnevas järjestuses:
- Pärisnimi on enamasti projektsiooni looja perekonnanimi, näiteks Lamberti projektsioon, Mercatori projektsioon, Petersi projektsioon.
- Iseloomulik tunnus on enamasti seotud projitseerimiskeskmega, näiteks tsentraalne projektsioon, perspektiivne projektsioon.
- Omadus on seotud moonutuse liigiga, näiteks konformne projektsioon, sobe projektsioon, õigepikkuseline projektsioon, õigepindne projektsioon.
- Klassi määrab siirdepind, näiteks silindriline projektsioon, kooniline projektsioon, asimutaalne projektsioon.
- Aspekt tuleneb siirdepinna asendist: näiteks põiksilindriline projektsioon.
- Vormiline tunnus on projektsioonile iseloomulik omadus, näiteks lahtilõigetega projektsioon.
Vaata ka
[muuda | muuda lähteteksti]- Rahvusvaheline geodeetiliste koordinaatide süsteem
- Kaardiprojektsioonide loend
- Kaart
- Kartograafia
- Geoinfosüsteem
Viited
[muuda | muuda lähteteksti]- ↑ R. Knippers. "Map Projections". Vaadatud 12.04.2017.
- ↑ 2,0 2,1 2,2 "Projektsiooni aspekt". Vaadatud 10.04.2017.
- ↑ "Kaardi projitseerimisviis". Vaadatud 10.04.2017.
- ↑ "Moonutused kaardil". Vaadatud 10.04.2017.
- ↑ Snyder, John P. (1993). Flattening the earth: two thousand years of map projections. University of Chicago Press. ISBN 0-226-76746-9.
- ↑ "Projektsiooni omadused". Vaadatud 10.04.2017.
Välislingid
[muuda | muuda lähteteksti]| Pildid, videod ja helifailid Commonsis: Kaardiprojektsioon |
