Ruutjuur kahest
Ruutjuur kahest ehk on positiivne reaalarv, mille korrutamine iseendaga annab arvu 2.
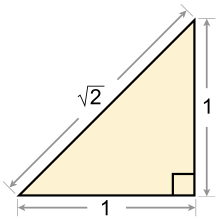
Geomeetriliselt on ruutjuur arvust kaks ruudu diagonaali pikkus, kui ruudu külje pikkus on 1 (selline ruut on ühikruut). Asjaolu ruudu diagonaali ja ruudu külje suhte kohta järeldub Pythagorase teoreemist (vaata joonist). See ruudu diagonaali ja külje suhtearv on tõenäoliselt esimene arv, mida teati olevat irratsionaalne. Selle arvväärtus kuni esimese 65 komakohani on[1]
- 1,41421 35623 73095 04880 16887 24209 69807 85696 71875 37694 80731 76679 73799....
Murd annab ligikaudse väärtuse kuni esimese nelja komakohani.
Ruutjuurt kahest on hiljuti hakatud nimetama ka Pythagorase konstandiks[2], sest Pythagorasele omistatakse avastus, et ruudu külje pikkus on ühismõõdutu ruudu diagonaali pikkusega.
Irratsionaalsuse tõestamine
[muuda | muuda lähteteksti]Tõestame ruutujuur kahe irratsionaalsuse vastuväiteliselt. Selleks eeldame, et √2 on ratsionaalarv, ning näitame, et see eeldus viib vastuoluni. Viimasest järeldub, et √2 ei saa olla ratsionaalarv ning on seega irratsionaalne.
- Kui √2 on ratsionaalarv, siis peavad leiduma sellised naturaalarvud m ja n, et √2 = m/n.
- Üldisust kitsendamata võib eeldada, et m/n on taandumatu murd, mis tähendab, et m ja n on ühistegurita.
- Võrduse √2 = m/n võib kirjutada kujul m2 = 2n2. Sellest järeldub aga, et m2 on paarisarv.
- Pannes tähele, et paarisarvu ruut on alati paarisarv ja paaritu arvu ruut on alati paaritu arv, võime punktist (3) järeldada, et ka m peab olema paarisarv. Seega on m esitatav kujul m = 2k, kus k on naturaalarv.
- Eelnevast leiame, et 2n2 = m2 = (2k)2 = 4k2. Ehk n2 = 2k2, mis lubab meil punktis (4) kasutatud argumentidele tuginedes öelda, et n jagub kahega.
- Kui nii m kui n jaguvad kahega, siis on 2 nende ühistegur, mis läheb vastuollu punktis (2) tehtud eeldusega, et n ja m on ühistegurita. √2 irratsionaalsus on tõestatud.
Antud tõestuse saab läbi viia ka eelduseta, et m ja n on ühistegurita. Selleks tuleb tähele panna, et punktides (3) ja (4) esitatud argumentide abil näitasime, et m jagub kahega (punkt (4)) ja et n jagub kahega (punkt (5)). Seda protsessi jätkates saab tuletada, et ka m/2, m/4, m/8 jne jagub kahega ning ehk m/(2k) jagub kahega. Jätkates seda protsessi jõuame olukorrani, kus m < 2k. On selge, et m/2k < 1 ei saa olla täisarv ning seega ei saa m/2k-1 kahega jaguda. See on aga vastuolu, mis tõestab, et √2 pole ratsionaalarv. Viimase tõestuse andis Eukleides.


