Des maths avec Python Chapitre 4

Chapitre 4
Zéros d'une fonction
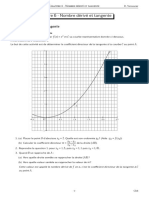
Trouver les zéros d'une fonction f, c'est déterminer à quelles abscisses cette fonction coupe l'axe
des x (points rouges dans l'image ci-dessous). Cela revient à résoudre l'équation f (x) = 0.

Or, selon la fonction, l'entreprise peut se révéler difficile, voir impossible, en utilisant des
méthodes algébriques. Pour les polynômes par exemple, Galois a montré qu'il n'existe pas de
formules pour les polynômes de degré supérieur à 4.
Dans ces cas, l'emploi de méthodes numériques est indispensable. Nous allons en voir quelques-
unes dans ce chapitre.

4.1. Recoupement par intervalles (bracketing)

Il s'agit de construire des intervalles susceptibles de contenir un zéro. Ultérieurement, on raffinera
la recherche du zéro à l'intérieur de l'intervalle.
On subdivise un domaine donné en sous-intervalles réguliers et on examine si la fonction
(supposée continue) coupe l'axe des x en regardant le signe de la fonction évaluée aux bords du sous-
intervalle.
Exercice 4.1
Programmez la méthode de bracketing, puis testez-la avec les fonctions f (x) = sin(cos(2x2+1)) et
g(x) = x5 – x2 -1, dans l'intervalle [0, 2], subdivisé en 20 sous-intervalles.

Didier Müller 4-1 mai 2019

 Zéros d'une fonction

4.2. Méthode de dichotomie

Une dichotomie (du grec « couper en deux ») permet de trouver rapidement une valeur approchée
de x telle que f (x) = 0. Cette méthode n'est pas sans rappeler le jeu « devine mon nombre » que nous
avons programmé au chapitre 2.

Petite astuce : Soit f une fonction telle que :

si f (a) et f (b) sont • f (a) et f (b) sont de signes opposés
de signes opposés,
alors f (a)·f (b) < 0. • f est continue strictement croissante (ou décroissante) sur [a, b]

Méthode
1. partir du couple de valeurs (a, b)
a+ b
2. évaluer la fonction en
2
3. si f ( )
a+ b
2
a le même signe que f (a), remplacer a par
a+ b
2
, sinon remplacer b par
a+ b
2
4. aller en 2 avec le nouveau couple de valeurs (a, b) jusqu'à ce que la différence entre a et b
soit inférieure à la précision voulue.
Exercice 4.2
Illustrez la dichotomie sur le graphe ci-dessous, pour trouver le zéro compris entre -1 et 0.
Idem pour le zéro compris entre 0 et 1.

Exercice 4.3
a) Calculez, avec la méthode de la dichotomie et à l'aide d'une calculatrice, le zéro de la
fonction sin(cos(2x2+1)) se trouvant dans l'intervalle [0, 1], avec une précision de 0.0001.
b) Programmez la dichotomie pour répondre à la question a).

Courbe de la fonction sin(cos(2x2+1))

Didier Müller 4-2 mai 2019

Des maths avec Python Chapitre 4

4.3. Regula falsi

Étant données les abscisses a et b, nous construisons la droite passant par les points (a, f (a)) et
(b, f (b)), comme dans la figure ci-dessous.

Remarquons que cette droite est une sécante de la fonction f. En utilisant la pente et un point,
l'équation de la droite peut s'écrire :

f ( b) – f (a)
y= ( x – a)+ f (a)
b–a

Nous déterminons maintenant c, l'abscisse du point d'intersection de cette droite avec l'axe des
abscisses (zéro de la sécante) donnée par :

f (b) – f ( a)
(c – a)+ f ( a)=0
b–a

La résolution de l'équation précédente donne c :

b–a
c=a – f (a)
f (b) – f ( a)

Déroulement du calcul
Comme la méthode de dichotomie, la regula falsi commence par deux points a1 et b1 tels que
f (a1) et f (b1) soient de signes opposés, ce qui implique que la fonction continue f possède au moins
un zéro dans l'intervalle [a1, b1]. La méthode consiste à produire une suite d'intervalles toujours plus
petits [ak, bk] qui contiennent tous un zéro de f. À l'étape k, le nombre

b k – ak
c k= ak – f (ak )
f ( b k ) – f ( ak )

est calculé. Comme expliqué ci-dessus, ck est l'abscisse de l'intersection de la droite passant par
(ak, f (ak)) et (bk, f (bk)) avec l'axe des abscisses. Si f (ak) et f (ck) sont de même signe, alors nous
posons ak+1 = ck et bk+1 = bk, sinon nous posons ak+1 = ak et bk+1 = ck.
Ce procédé est répété jusqu'à ce f (ck) soit « suffisamment proche » de 0.

Didier Müller 4-3 mai 2019

 Zéros d'une fonction

Exercice 4.4
Illustrez le déroulement de la regula falsi sur le graphe ci-dessous, pour trouver le zéro compris
entre 0 et 1.

Exercice 4.5
a) Trouvez, avec la méthode de la regula falsi et à l'aide d'une calculatrice, le zéro de la
fonction sin(cos(2x2+1)) se trouvant dans l'intervalle [0, 1], avec une précision de 0.0001.
b) Programmez la regula falsi pour répondre à la question a).

4.4. Méthode de Newton-Raphson

En analyse numérique, la méthode de Newton-Raphson, est un algorithme efficace pour
approcher un zéro d'une fonction. De manière informelle, le nombre de décimales correctes double à
chaque étape.
Partant d'une valeur approximative raisonnable d'un zéro x0 d'une fonction f, on approche la
fonction par sa tangente au point (x0 ; f (x0)). Cette tangente est une fonction affine dont on sait
trouver l'unique zéro (que l'on appellera x1). Ce zéro de la tangente sera généralement plus proche du
« vrai » zéro de la fonction.
On recommence les mêmes calculs en partant cette fois de x1, ce qui va nous donner l'abscisse x2,
etc.

Didier Müller 4-4 mai 2019

Des maths avec Python Chapitre 4

f  xn
Par récurrence, on définit la suite xn par : x n1 = xn – .
f '  x n
En principe, cette suite va converger vers le zéro cherché.
Si la fonction présente un extremum local, il y a un risque que la méthode ne converge pas, car la
valeur de la dérivée est nulle en un extremum et le nouveau point à l'infini.
Exercice 4.6
Retrouvez la valeur de xn+1 en partant de l'équation de la droite y-y0 = m(x-x0).
La pente m de la tangente en a est donnée par la dérivée f ' (a).
Exercice 4.7
Illustrez le déroulement de la méthode de Newton-Raphson sur le graphe ci-dessous...
a) avec x0 = -0.25 ;
b) avec x0 = 0.

Exercice 4.8
a) Calculez, avec la méthode de Newton-Raphson et à l'aide d'une calculatrice, le zéro de la
fonction f (x) = sin(cos(2x2+1)) se trouvant dans l'intervalle [0 ; 1], avec une précision de
0.0001.
Indication : f ' (x) = -4x·cos(cos(2x2+1))·sin(2x2+1).
b) Programmez la méthode de Newton-Raphson pour répondre à la question a).
c) Expliquez ce qui se passe en prenant x0 = 1, x0 = 1.1, et x0 = 1.2.

4.5. Méthode de la sécante

La méthode de la sécante est une méthode dérivée de celle de Newton-Raphson où l'on remplace
f ( x n) – f ( x n – 1)
la dérivée f ' ( x n ) par .
xn – x n – 1
xn – x n – 1
On obtient la relation de récurrence x n+ 1 = xn − f ( xn ) .
f ( x n) – f ( x n – 1)

L'initialisation nécessite deux points x0 et x1 proches de la solution recherchée. Il n'est pas

nécessaire que x0 et x1 encadrent une racine de f (x).

Didier Müller 4-5 mai 2019

 Zéros d'une fonction

Exercice 4.9
Illustrez le déroulement de la méthode de la sécante sur le graphe ci-dessous avec x0 = -0.7 et
x1 = -0.25.

Exercice 4.10
a) Calculez, avec la méthode de la sécante et à l'aide d'une calculatrice, le zéro de la fonction
f (x) = sin(cos(2x2+1)) se trouvant dans l'intervalle [0, 1], avec une précision de 0.0001.
b) Programmez la méthode de la sécante pour répondre à la question a).
c) Expliquez ce qui se passe en prenant x0 = 0 et x1 = 2.

4.6. Programmation d'un traceur de courbe

Un traceur de courbes (on dit aussi parfois un grapheur) est un logiciel qui permet de calculer et
dessiner et la courbe représentative d'une fonction mathématique.
Pour réaliser un tel logiciel en Python, il nous faudra quelques fonctions graphiques contenues
dans le module tkinter. Il s'agira essentiellement de tracer des segments de droite.
Voyons comment ouvrir une fenêtre graphique et dessiner un segment à l'écran :

Didier Müller 4-6 mai 2019

Des maths avec Python Chapitre 4

from tkinter import *

fen = Tk()
can = Canvas(fen, bg='white', width=600, height=400)
can.pack(side=LEFT)
can.create_line(10, 10, 100, 200, width=2, fill='black') # segment
can.create_text(10, 5, text="A")
can.create_text(100, 205, text="B")

Reprenons ce programme ligne par ligne.

from tkinter import *

tkinter est le module qui permet de dessiner.

fen = Tk()

fen est la fenêtre graphique.

can = Canvas(fen, bg='white', width=600, height=400)

can est le canevas dans lequel on va dessiner. Ici, il occupera toute le fenêtre. Il a un fond blanc
(white) et pour dimensions 600 x 400 pixels.

can.pack(side=LEFT)

can est calé à gauche de la fenêtre, mais cela n'a pas d'importance ici.

can.create_line(10, 10, 100, 200, width=2, fill='black') # segment

Dans l'exemple, le segment va du point (10, 10) au point (100, 200). Il a une largeur de 2 pixels et
la couleur noire (black). On utilisera black pour les axes et les graduations, blue pour la courbe,
white comme couleur de fond et gray75 pour le quadrillage.
Attention ! L'origine (0, 0) est dans le coin supérieur gauche de la fenêtre. Le coin inférieur droit
aura comme coordonnées (largeur, hauteur), dans notre exemple (600, 400).

can.create_text(10, 5, text="A")
can.create_text(100, 205, text="B")

Ces deux lignes écrivent les lettres A et B aux coordonnées indiquées.

Si on veut écrire un nombre contenu dans une variable, il faudra convertir ce nombre en une
chaîne de caractères :

i = 4
can.create_text(100, 205, text=str(i))

Exercice 4.11
Pour simplifier les choses, on supposera que la fonction f à dessiner est continue. Pour fixer les
idées, prenons la fonction f (x) = x + sin(x2 + 4x – 5).
On supposera aussi que les bornes de l'intervalle [a, b] sont des nombres entiers. On prendra ici
l'intervalle [–6, 3].
Procédez par étapes :
1. tabulez la fonction dans l'intervalle [a, b] et repérez les valeurs y_min et y_max ;
2. définissez la fonction affine qui transformera le couple (x ; f (x)) en un point de la fenêtre
graphique ; le couple (a ; y_max) sera envoyé sur le point (0 ; 0) et le couple (b ; y_min) sur
le point (largeur, hauteur).
3. tracez la courbe ;
4. dessinez les deux axes ;
5. graduez les axes ;
6. ajoutez un quadrillage.

Didier Müller 4-7 mai 2019

 Zéros d'une fonction

Voici le résultat final attendu :

4.7. Suites de Sturm

Soit P(x) un polynôme n'ayant que des racines simples. La suite de Sturm de ce polynôme est
une suite de polynômes qui permet de déterminer le nombre de racines de P dans un intervalle
donné.
On pose d'abord P0 = P et P1 = P ′. Pour calculer P2, on écrit :

Charles-François P0 = P1Q1 − P2
Sturm (1803-1855)
où Q1 est le quotient de la division euclidienne et où le degré de P2 est strictement inférieur à
celui de P1.

En d'autres termes, P2 est l'opposé du reste dans la division euclidienne de P0 par P1. Puis on
recommence et on définit Pk+1 comme l'opposé du reste dans la division euclidienne de Pk-1 par Pk,

Pk-1 = PkQk − Pk+1 .

On s'arrête lorsqu'on obtient un polynôme constant Pn, ce qui arrive forcément puisque les degrés
des polynômes obtenus décroissent à chaque division. La suite de Sturm du polynôme P est alors :

S (x) = (P0(x), P1(x), …, Pn(x)).

On note V (x) le nombre de changements de signes dans la suite S (x).

Le théorème de Sturm s'énonce à présent ainsi :

Le nombre de racines de P dans l'intervalle [a, b] est égal à la différence V (a) − V (b).

Didier Müller 4-8 mai 2019

Des maths avec Python Chapitre 4

Exemple : Soit P (x) = x3 + 6x2 − 16. On a P0 = P, P1 = P '(x) = 3x2 + 12x.

Pour trouver P2, on divise P0 par P1 :

P0 x3 + 6x2 – 16 | 3x2 + 12x P1

– x3 – 4x2 x/3 + 2/3 Q1
2x2
– 2x2 – 8x
– 8x – 16 -P2

On trouve P2 = – (–8x – 16) = 8x + 16.

Pour trouver P3, on divise P1 par P2 :

P1 3x2 + 12x | 8x + 16 P2
2
– 3x – 6x 3x/8 + 3/4 Q2
6x
– 6x – 12
– 12 -P3

On trouve P3 = – (–12) = 12. Le processus s'arrête ici, puisque P3 est un polynôme constant.

On a trouvé la suite de Sturm de P : S (x) = (x3 + 6x2 − 16, 3x2 + 12x, 8x + 16, 12).

On peut maintenant savoir combien P a de zéros dans l'intervalle [a, b]. Prenons par exemple
l'intervalle [−7, 2] :

S (−7) = (−65, 63, −40, 12). Il y a 3 changements de signe

dans cette suite, donc V (−7) = 3.
S (2) = (16, 36, 32, 12). Cette fois, il n'y a pas de
changement de signe, donc V (2) = 0.
Comme V (−7)−V (2) = 3, le polynôme x3 + 6x2 − 16 admet
ses 3 racines dans l'intervalle [−7, 2].

Dans l'intervalle [0, 2] :

S (0) = (−16, 0, 16, 12). Il y a un seul changement de signe dans cette suite, donc V(0) = 1.
Puisque V (0)−V (2) = 1, le polynôme x3 + 6x2 − 16 admet une racine dans l'intervalle [0, 2].
Exercice 4.12
Calculez la suite de Sturm du polynôme P (x) = x4 – 8x2 – 6x – 1.
Grâce à cette suite, déterminez le nombre de zéros de P dans les intervalles [–4, 0] et [0, 4].
Vérifiez ces résultats avec votre traceur de courbe.

Sources
[1] Wikipédia, « Méthode de dichotomie », <http://fr.wikipedia.org/wiki/Méthode_de_dichotomie>
[2] Wikipédia, « Méthode de la fausse position »,
<http://fr.wikipedia.org/wiki/Méthode_de_la_fausse_position>
[3] Wikipédia, « Méthode de la sécante », <http://fr.wikipedia.org/wiki/Méthode_de_la_sécante>
[4] Science & Vie Questions Réponses, Hors-Série N°1, novembre 2016, « Équations du second
degré »

Didier Müller 4-9 mai 2019