- Реализовать численное нахождение определённых интегралов от произвольной функции (квадратурные формулы треугольников, трапеций, Симпсона).
- Выполнить тестирование на 8 различных тестовых интегралах. Сравнить погрешности полученных результатов. (Интегралы для точной оценки можно вычислить в ручную)
- Построить графики функций и квадратур. Сравнить погрешности полученных для различного числа точек, разбивающих отрезок.
Краткое описание выполнения задания:
-
Создаем форму и обработчики событий.
-
Определяем основной класс программы.
- Класс - математическая функция которую нужно проинтегрировать.
Область определения функций это наш отезок интегрирования от a до b с указанным шагом.
Область значений это массив значений выбранной функции, которые она принимает при переборе всех x из области определения.
Используемые методы:
- Метод трапеций
- Метод центральных прямоугольников.
- Метод Симпсона
-
Определяем массив из 8 функций которые хотим проинтегрировать:
- y=sin(x)
- y=cos(x)
- y=2*x²
- y=x
- y=5ᵡ
- y=1/5²+x²
- y=eᵡ
- y=(x+2)³
-
Оцениваем погрешности для двух первых методов по формулам:
Использовать при отображении погорешностей знак ± мы считаем уместным, так как при вычислении второй производной была использована приближенная формула для вычисления производной, которая тоже зависит от выбранной точности интегрирования и дает собственную погрешность.
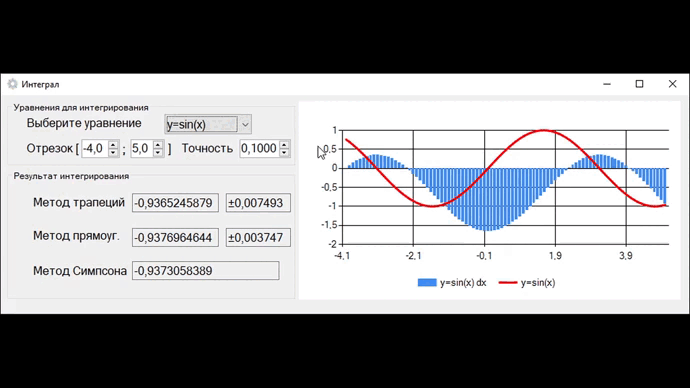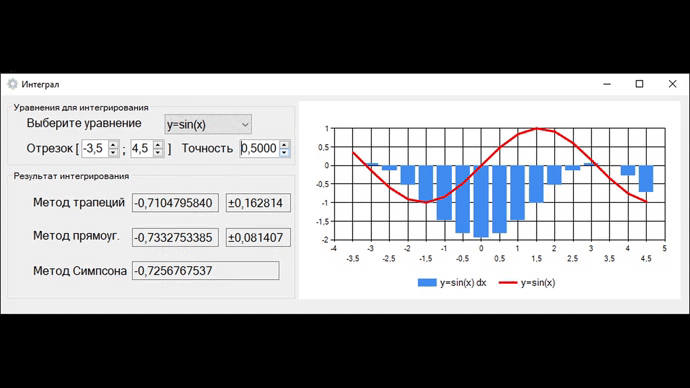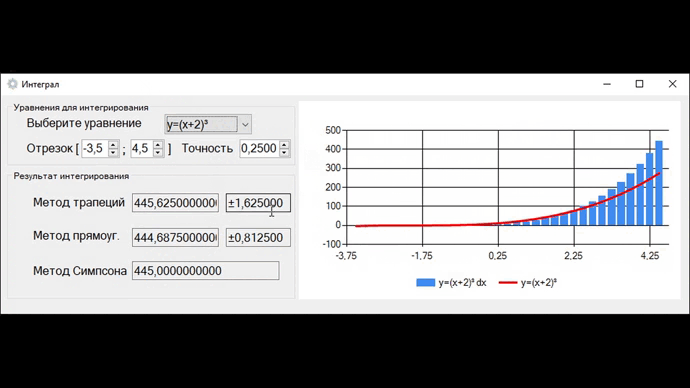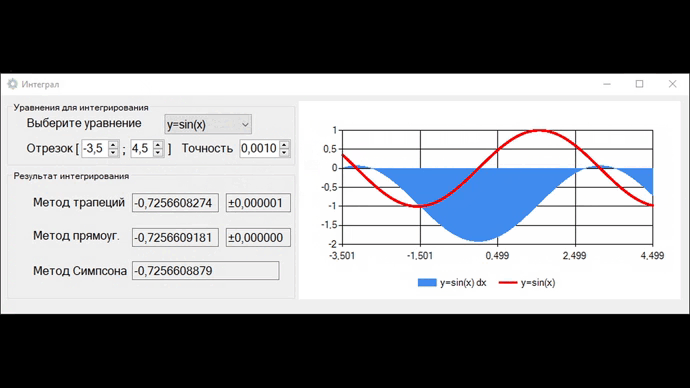
Графики строятся по результатам метода центральных прямоугольников (это видно если увеличить точность до 0,5).
- Общий функционал
default.mp4
На выходе получаем программу, которая тремя методами высчитывает значения интегралов для 8 заданных функций, и на их основе строит графики. При уменьшении шага h в 2 раза погрешность методов трапеций и прямоугольников уменьшится в 4 раза, что видно на видео.
- Конопченко Л.Б | Работа с кодом (C++ CLR) | Документация проекта
- Рау М.А | Документация проекта