Structure-Preserving Signatures and Commitments to Group Elements

Abstract

A modular approach to constructing cryptographic protocols leads to simple designs but often inefficient instantiations. On the other hand, ad hoc constructions may yield efficient protocols at the cost of losing conceptual simplicity. We suggest a new design paradigm, structure-preserving cryptography, that provides a way to construct modular protocols with reasonable efficiency while retaining conceptual simplicity. A cryptographic scheme over a bilinear group is called structure-preserving if its public inputs and outputs consist of elements from the bilinear groups and their consistency can be verified by evaluating pairing-product equations. As structure-preserving schemes smoothly interoperate with each other, they are useful as building blocks in modular design of cryptographic applications. This paper introduces structure-preserving commitment and signature schemes over bilinear groups with several desirable properties. The commitment schemes include homomorphic, trapdoor and length-reducing commitments to group elements, and the structure-preserving signature schemes are the first ones that yield constant-size signatures on multiple group elements. A structure-preserving signature scheme is called automorphic if the public keys lie in the message space, which cannot be achieved by compressing inputs via a cryptographic hash function, as this would destroy the mathematical structure we are trying to preserve. Automorphic signatures can be used for building certification chains underlying privacy-preserving protocols. Among a vast number of applications of structure-preserving protocols, we present an efficient round-optimal blind-signature scheme and a group signature scheme with an efficient and concurrently secure protocol for enrolling new members.

1 Introduction

1.1 Structure-Preserving Cryptography

Cryptographic protocols often use modular constructions that combine general building blocks such as commitments, encryption, signatures, and zero-knowledge proofs. Modular design is useful to show the feasibility of realizing a particular security goal and may lead to simpler security proofs that are less error-prone than seen in ad hoc constructions. On the other hand, modular design can incur a significant overhead, and in feasibility proofs efficient instantiations are often left as the next challenge. This challenge is often solved by finding a “cleverly crafted” efficient solution for the specific security goal. However, modular constructions make it easier to design and understand protocols. It is therefore desirable to have a framework of interoperable building blocks with efficient instantiations such that we can design protocols that are both modular and efficient at the same time.

Since the seminal works in [24, 63, 86], bilinear groups have been widely used for constructing efficient cryptographic protocols. However, protocols defined over bilinear group are not necessarily compatible with each other as they may involve both group and field elements in different places as well as additional cryptographic primitives such as collision-resistant hash functions for instance.

We propose structure-preserving cryptography as an approach for efficiently instantiating modular constructions over bilinear groups $\Lambda := (p,{{\mathbb {G}}},\tilde{{{\mathbb {G}}}},{{\mathbb {G}}}_T,e,G,\tilde{G})$ where ${{\mathbb {G}}}, \tilde{{{\mathbb {G}}}}$ and ${{\mathbb {G}}}_T$ are groups of prime order $p$ generated by $G, \tilde{G}$ and $e(G,\tilde{G})$, respectively, with a bilinear map $e:{{\mathbb {G}}}\times \tilde{{{\mathbb {G}}}}\rightarrow {{\mathbb {G}}}_T$. In structure-preserving cryptography, building blocks are designed over common bilinear groups $\Lambda$ such that

• all public objects such as public keys, messages, signatures, commitments and ciphertexts are elements of the groups ${{\mathbb {G}}}$ and $\tilde{{{\mathbb {G}}}}$, and

• verifying relations of interest, such as signature verification or opening of a commitment, can be done by performing group operations and evaluating pairing-product equations of the form

  $$\begin{aligned} \textstyle \prod \limits _{i}\prod \limits _{j} e(X_i,\tilde{Y}_j)^{c_{i,j}} \;=\; 1, \end{aligned}$$

  where $c_{i,j} \in {{\mathbb {Z}}}$ are constants specified by the scheme.

We call cryptographic schemes satisfying these conditions structure-preserving. It will sometimes be useful to consider also relaxed structure preservation where public elements in the target group ${{\mathbb {G}}}_T$ are permitted as well and where pairing-product equations may be of the form $\prod _i\prod _je(X_i,\tilde{Y}_j)^{c_{i,j}}=T$ with $T\in {{\mathbb {G}}}_T$.

The properties defining structure preservation are preserved by modular constructions. Namely, a scheme built by modularly combining (relaxed) structure-preserving building blocks is (relaxed) structure-preserving as well. They therefore offer strong compatibility and modularity. On the other hand, the restrictive properties make it more challenging to design structure-preserving schemes. In particular, structure-preserving cryptography inherently prohibits the use of collision-resistant hash functions that break the underlying mathematical structure of the bilinear groups.

Combining non-interactive proofs with other primitives is a typical approach in modular construction of secure cryptographic protocols. A classical way of realizing efficient instantiations is to rely on the random-oracle heuristic [18] for non-interactive proofs—or to directly use interactive assumptions like (variations of) the LRSW assumption [78] and “one-more” assumptions [17]. Due to a series of criticisms starting with [37], more and more practical schemes are being proposed and proved secure in the standard model (i.e., without random oracles) and under falsifiable (and thus non-interactive) intractability assumptions [80]. In [59], Groth and Sahai presented the first (and currently the only) efficient non-interactive proof system based on standard assumptions in bilinear groups. Their proof system, called GS for short, exerts its full power as a non-interactive proof-of-knowledge system when the proof statement is a set of relations described by pairing-product equations, for which the witnesses are group elements in the source groups, that is ${{\mathbb {G}}}$ and $\tilde{{{\mathbb {G}}}}$. Due to these limitations, however, many existing cryptographic schemes cannot be modularly combined with GS proofs. In contrast, structure-preserving schemes are defined so that they are compatible with the GS proof system. Accordingly, by using GS proofs, one can efficiently prove one’s knowledge about the witness for relations of interest in structure-preserving schemes.

We address two major building blocks in cryptographic protocol design, commitment schemes and signature schemes, and present their structure-preserving instantiations with several useful properties as explained in the following.

1.2 Homomorphic Trapdoor Commitments

A non-interactive commitment scheme allows a sender to create a commitment to a message. The commitment hides the message but the sender may later choose to open the commitment to the message. A commitment is bound to a message in the sense that a commitment cannot be opened to two different messages. On top of the fundamental properties of hiding and binding, a commitment may have other desirable features. In a trapdoor commitment scheme [60, 83], a certain piece of trapdoor information makes it possible to circumvent the binding property and open a commitment to an arbitrary message. In a homomorphic commitment scheme, messages and commitments belong to abelian groups, and by multiplying two commitments, we obtain a commitment to the product of the committed messages. Finally, a commitment scheme is often required to be length-reducing such that the commitment is shorter than the message.

An example that provides all those properties is a generalization of Pedersen commitments [83] where a message is a vector of values in $\mathbb {Z}_p$ and a commitment consists of only one group element. Such commitments have been found useful in contexts such as mix-nets, voting, digital credentials, blind signatures, leakage-resilient one-way functions and zero-knowledge proofs [11, 30, 50, 66, 77, 81].

We present structure-preserving commitment schemes whose public keys, messages, commitments and openings are elements of bilinear groups, and whose opening is verified by evaluating pairing-product equations. Our commitments are trapdoor and homomorphic, and some of them are length-reducing as well. The attributes that discriminate our constructions are the types of bilinear groups used and the groups that messages and commitments belong to. (See Table 1 on page 21 for a summary.)

• The first and the second homomorphic trapdoor commitment schemes are length-reducing by mapping vectors of source-group elements to a constant number of target-group elements and thus relaxed structure-preserving.

• The third homomorphic trapdoor commitment scheme is strictly structure-preserving, which means both messages and commitments consists of source-group elements. They are, however, not length-reducing.

• The last commitment scheme takes messages from $\mathbb {Z}_p$ and maps them to a single source-group element. This scheme is by definition not structure-preserving though all other properties are provided. We include it here for its usefulness as a building block for applications.

Our commitment schemes can be used to build structure-preserving one-time signatures, as we demonstrate in Sect. 4. The first two length-reducing schemes are useful in reducing the size of zero-knowledge arguments. Groth [58] showed that the square-root-size zero-knowledge arguments in [57] can be reduced to cubic-root-size zero-knowledge arguments by using our homomorphic trapdoor commitments. We explore this topic in Sect. 3.1.

There are follow-up works about structure-preserving commitments. In [9], it is proved that strictly structure-preserving commitment schemes cannot yield commitments that are shorter than messages; a commitment to a $k$-element message must have more than $k$ elements itself. This should be contrasted with the relaxed structure-preserving commitment schemes we give, where a commitment to a $k$-element message consists of a small constant number of target-group elements.

1.3 Signatures

A signature scheme is called structure-preserving if the public verification keys, messages, and signatures are source-group elements of bilinear groups, and the verification of a signature consists of evaluating pairing-product equations. It is called automorphic if in addition its verification keys lie in its message space. There are many applications using combinations of digital signatures and non-interactive zero-knowledge proofs of knowledge such as blind signatures [10, 43], group signatures [16, 19, 68], anonymous credential systems [15], verifiably encrypted signatures [26, 85], non-interactive group encryption [38] and so on, and structure-preserving signatures are ideally suited for these applications.

Research on structure-preserving signature schemes was initiated by Groth [54], who gave the first feasibility result based on the decision linear assumption (DLIN) [23]. His structure-preserving signature scheme yields a signature of size ${\mathcal {O}}(k)$ when the message consists of $k$ group elements. While it is remarkable that the security can be based on a simple standard assumption, the scheme is not practical due to its large constant factor. Based on the $q$-Hidden LRSW assumption for asymmetric bilinear groups, Green and Hohenberger [53] presented a structure-preserving signature scheme that only provides security against random-message attacks. Unfortunately, an extension to chosen-message attack security is not known. In [38], Cathalo et al. gave a scheme with relaxed structure preservation based on a combination of the Hidden Strong Diffie–Hellman Assumption (HSDH), the Flexible Diffie–Hellman Assumption, and the DLIN assumption. Their signature consists of $9 {k}+ 4$ group elements for a $k$-element message, and it was left as an open problem to construct constant-size signatures. There are also several signature schemes, such as [15, 22, 31, 35], where validity is defined via pairing-product equations, but whose signatures do not only contain group elements.

We present several constructions of structure-preserving signatures with high efficiency and useful properties.

• Structure-PreservingOne-Time Signatures. We construct two signature schemes that are existentially unforgeable when the adversary is only allowed one signing query. The schemes are currently the most efficient in the literature, and their security follows from the decision Diffie–Hellman and the decision linear assumptions, respectively.

• Constant-Size Structure-Preserving Signatures. We construct the first constant-size structure-preserving signature scheme. A signature consists of 7 group elements independently of the message length and the verifier needs to check two pairing-product equations. Existential unforgeability against adaptive chosen-message attacks is proven under a new non-interactive assumption called the Simultaneous Flexible Pairing Assumption (SFP).

• Automorphic Signatures. We construct the first automorphic signature scheme, whose signatures consist of 5 group elements. We prove the scheme existentially unforgeable against adaptive chosen-message attacks under a variant of the Strong Diffie–Hellman assumption [22].

After the publication of [5], structure-preserving signatures have been intensively studied. Several constructions over asymmetric bilinear groups, i.e., where ${{\mathbb {G}}}\ne \tilde{{{\mathbb {G}}}}$, are presented in [6]. The latter shows that there is a scheme whose signature consists of only 3 group elements when the security is directly proven in the generic bilinear-group model. It also presents a scheme with 4-element signatures, which is $3$ group elements fewer compared to our scheme in Sect. 5.1. Its security is based on a non-interactive assumption that is, however, not known to be as tight as the discrete-logarithm assumption when assessed in the generic bilinear-group model. This is the case for the assumption ($q$-SFP in Sect. 2.5) that implies security of our scheme.

Significant theoretical advances are made in [2, 3], which present structure-preserving signature schemes based on compact and static, i.e., not $q$-type, assumptions such as the decision linear assumption. The schemes are over symmetric and asymmetric bilinear groups and yield signatures consisting of 11 to 14 group elements.

1.4 Applications

The usefulness of structure-preserving cryptography as a design paradigm is demonstrated by a growing list of applications including round-optimal blind signatures [5, 49], group signatures with concurrent join [5, 49, 72, 73], homomorphic signatures [14, 71], anonymous proxy signatures [47], delegatable anonymous credentials [46], direct anonymous attestation [20], transferable e-cash [21, 48], conditional e-cash [89], compact verifiable shuffles [39], network coding [13], oblivious transfer [1, 33, 53], chosen-ciphertext-secure encryption [3, 34, 62] and many more. Among this vast number of applications, we present group signatures and blind signatures in this paper.

1.4.1 Group Signatures with Concurrent Join

We give a modular structure-preserving construction of group signatures [41] supporting a concurrent join procedure [68] for enrolling new members.

A group signature scheme is a classical primitive ensuring user anonymity. It allows members that were enrolled by a group manager to sign on behalf of a group without revealing their identity. To prevent misuse, anonymity can be revoked by an authority. There are numerous constructions of group signature schemes in the literature providing different properties. However, previous constructions are not in the standard model, do not provide a concurrent join procedure, lack some important property like non-frameability or are inefficient. The scheme in [68] is the first one that allows efficient concurrent join, but its security relies on the random-oracle model [18]. The scheme in [12] is non-frameable but only allows new members to join sequentially and is based on strong interactive assumptions. Both [28, 29] provide efficiency with reasonable assumptions but the group manager enrolling members knows their secret keys and can thus frame them by creating signatures using their keys. The scheme in [55] is non-frameable but does not allow concurrent join. More recent papers, such as [42, 75, 76], focus on advanced properties leaving one or more of the above issues unaddressed.

1.4.2 Round-Optimal Blind Signatures

Blind signatures, introduced by Chaum [40], allow a user to obtain a signature on a message such that the signer cannot relate the resulting signature to the execution of the signing protocol. They were formalized by [64, 84] and practical schemes without random oracles have been constructed in e.g., [36, 66, 67, 82]. However, all these schemes require more than one round (i.e., two moves) of communication between the user and the signer to issue a blind signature. This is even the case for most instantiations in the random-oracle model, an exception being Chaum’s scheme proved secure in [17] under an interactive assumption.

In [43], Fischlin gives a generic construction of round-optimal blind signatures in the common reference string (CRS) model; the signing protocol consists of one message from the user to the signer and one response by the signer. This immediately implies concurrent security, an explicit goal in other works such as [61]. Before our work, a practical instantiation of round-optimal blind signatures in the standard model was an open problem. Using our automorphic signature scheme, we provide the first efficient instantiation, which is the basis for commuting signatures and verifiable encryption in [46].

1.5 Correspondence to Preliminary Papers and Organization

This paper is based on three papers [7, 45, 56] submitted separately to crypto 2010 and presented as a merged paper [5], in which the term “structure-preserving signatures” is introduced. In [56], Groth presented the first homomorphic trapdoor commitments to group elements which are, moreover, length-reducing. Fuchsbauer [45] gave the first efficient structure-preserving signatures and used them to efficiently implement round-optimal blind signatures in the standard model. Abe et al. [7] then gave the first constant-size signature scheme on vectors of general group elements and constructed a group signature scheme with concurrently secure enrollment of new members.

Section 2 introduces notations, security notions and building blocks used in this paper. It includes, in Sect. 2.7, a useful technique that appeared in [7]. Section 3 features several homomorphic trapdoor commitment schemes, which originate from [7, 56]. Section 4 presents one-time signature schemes from [7], which can be a warm-up to the fully fledged structure-preserving signature scheme in Sect. 5. In Sect. 6, we present the automorphic signature scheme from [45] with a technique from [8] to extend the message space. Finally, Sect. 7 contains applications discussed above: the group signature scheme and the blind-signature scheme which originally appeared in [7] and [45], respectively.

2 Preliminaries

2.1 Notation

For a set $S$, $x \leftarrow S$ denotes assigning to $x$ a uniformly random value in $S$. Similarly, $x_1,\dots ,x_k \leftarrow S$ means independent uniformly random selection of $k$ elements from $S$. For a probabilistic algorithm $A$, we write $y:=A(x;r)$ for assigning $y$ the value of the output of the algorithm when running it on input $x$ using randomness $r$. We write $y\leftarrow A(x)$ for the process of picking uniformly random $r$ and setting $y:=A(x;r)$.

By $\Pr [y\leftarrow \mathrm {Exp}(x): \mathrm {Cond}(y)]$, we denote the probability that the condition $\mathrm {Cond}$ holds for the output $y$ of running the experiment $\mathrm {Exp}$ on some input $x$. The probability is taken over all coin flips used in the experiment $\mathrm {Exp}$. Typically, the input $x$ will be of the form $1^\lambda$, where $\lambda \in \mathbb {N}$ is a security parameter. We say $f:\mathbb {N}\rightarrow [0,1]$ is negligible if $f(\lambda )=\lambda ^{-\omega (1)}$ and $g:\mathbb {N}\rightarrow [0,1]$ is overwhelming if $g(\lambda )=1-f(\lambda )$ for some negligible function $f$. When defining security, we require the attacker’s success probability to be negligible as a function of the security parameter.

We will work over groups ${{\mathbb {G}}},\tilde{{{\mathbb {G}}}},{{\mathbb {G}}}_T$ of prime order $p$, which we denote multiplicatively. We will in general denote group elements by capital letters, i.e., $R\in {{\mathbb {G}}}, \tilde{S}\in \tilde{{{\mathbb {G}}}}, T\in {{\mathbb {G}}}_T$. Integers modulo $p$ will be denoted by lower case or Greek letters. We define ${{\mathbb {G}}}^*={{\mathbb {G}}}{\setminus } \{1\}$, $\tilde{{{\mathbb {G}}}}^*=\tilde{{{\mathbb {G}}}}{\setminus } \{1\}$ and ${{\mathbb {G}}}_T^*={{\mathbb {G}}}_T{\setminus } \{1\}$. When $\vec {X}$ is a tuple of group elements, $|{\vec {X}}|$ denotes the number of elements in $\vec {X}$.

When a group element is given as input to a function, its group membership must be tested. If the test fails, the function should output a special symbol that means rejection of the input. For conciseness of the description, we treat this procedure as implicit throughout the paper.

2.2 Commitment Schemes

A commitment scheme allows a sender to commit to a secret message $msg$. Later the sender may open the commitment and reveal the value $msg$ to the receiver. We focus on non-interactive commitment schemes where the sender and receiver do not need to interact to commit or to open commitments; both the commitment and the opening are bitstrings generated by the sender without interacting with the receiver.

We rely on a trusted setup phase where joint system parameters are generated and a commitment key is produced. We deliberately separate the setup phase in two parts $\mathsf{Setup }$ and $\mathsf{Key }$ to distinguish joint system parameters (which in our schemes will contain a description of bilinear groups that may be shared with other protocols such as signature schemes, encryption schemes) and the commitment key, which is specific to the commitment scheme.

Definition 1

(Trapdoor Commitment Scheme) We define a non-interactive trapdoor commitment scheme C as a tuple of polynomial-time algorithms ${\mathsf {C}}=(\mathsf {Setup}, \mathsf {Key}, \mathsf {Com}, \mathsf {Vrf}, \mathsf {Sim}, \mathsf {Equiv})$ in which:

• $gk \leftarrow \mathsf{Setup }(1^\lambda )$ is a common-parameter generator that takes security parameter $\lambda$ and outputs a set of common parameters, $gk$.

• $( ck , tk ) \leftarrow \mathsf{Key }( gk )$ is a key generator that takes $gk$ as input and outputs a commitment key $ck$ and a trapdoor key $tk$. The commitment key $ck$ determines the message space ${\mathcal {M}}_ ck$, the commitment space ${\mathcal {C}}_ ck$ and the opening space ${\mathcal {O}}_ ck$.

• $( com , open )\leftarrow \mathsf{Com }( ck , msg )$ is a commitment algorithm that takes $ck$ and message $msg \in {\mathcal {M}}_ ck$ and outputs a commitment $com \in {\mathcal {C}}_ ck$ and an opening $open \in {\mathcal {O}}_ ck$.

• $1/0 \leftarrow \mathsf{Vrf }( ck , com , msg , open )$ is a verification algorithm that takes $ck$, $com \in {\mathcal {C}}_ ck$, $msg \in {\mathcal {M}}_ ck$ and $open \in {\mathcal {O}}_ ck$ as input and outputs $1$ or $0$ representing acceptance or rejection, respectively.

• $( com , ek )\leftarrow \mathsf{Sim }(ck)$ takes commitment key $ck$ and outputs commitment $com \in {\mathcal {C}}_ ck$ and equivocation key $ek$.

• $open \leftarrow \mathsf{Equiv }( ck , msg , ek , tk )$ takes $ck , ek , tk$ and $msg \in {\mathcal {M}}_ ck$ as input and returns an opening $open$.

For correctness, it must hold that for all $\lambda \in \mathbb {N}$:

$$\begin{aligned} \Pr \left[ \begin{array}{l} gk \leftarrow \mathsf{Setup }(1^\lambda );\; ( ck , tk ) \leftarrow \mathsf{Key }( gk ) \\ msg \leftarrow {\mathcal {M}}_ ck ;\; ( com , open )\leftarrow \mathsf{Com }( ck , msg )\end{array}: 1 \leftarrow \mathsf{Vrf }( ck , com , msg , open )\right] = 1. \end{aligned}$$

For perfect trapdoor commitment schemes, the experiment $\{ gk \leftarrow \mathsf{Setup }(1^\lambda )$; $( ck , tk ) \leftarrow \mathsf{Key }( gk )$; $msg \leftarrow {\mathcal {M}}_ ck$; $( com , open ) \leftarrow \mathsf{Com }( ck , msg )$; $( com ', ek ) \leftarrow \mathsf{Sim }( ck )$; $open ' \leftarrow \mathsf{Equiv }( ck , msg , ek , tk )\}$ must yield identical probability distributions for $( ck , msg , com , open )$ and $( ck , msg , com ', open ')$.

In this paper, we consider $\mathsf{Vrf }$ as deterministic and say that $( msg , com , open )$ is valid with respect to $ck$ if $1 \leftarrow \mathsf{Vrf }( ck , com , msg , open )$. It follows from the correctness of the commitment scheme that in a perfect trapdoor commitment scheme, the equivocation of a trapdoor commitment will be accepted by the verifier.

Commitment schemes must be hiding and binding. Since commitments generated by $\mathsf{Sim }$ do not contain any information about the message, a perfect trapdoor commitment scheme is perfectly hiding in the sense that legitimate commitments do not reveal anything about the message. For the binding property, we use the following standard definition.

Definition 2

(Binding) A commitment scheme is computationally binding if for any probabilistic polynomial-time adversary ${\mathcal {A}}$

$$\begin{aligned} \Pr \left[ \begin{array}{l} gk \leftarrow \mathsf{Setup }(1^\lambda ); ck \leftarrow \mathsf{Key }( gk )\\ ( com , msg , open , msg ', open ') \leftarrow {\mathcal {A}}( ck )\end{array}:\begin{array}{l} msg \ne msg ' \\ 1 \leftarrow \mathsf{Vrf }( ck , com , msg , open ) \\ 1 \leftarrow \mathsf{Vrf }( ck , com , msg ', open ')\end{array} \right] \end{aligned}$$

is negligible.

Definition 1 follows a typical definition of a trapdoor commitment scheme with a simulation algorithm $\mathsf{Sim }$ that generates fake commitments. A slightly stronger definition referred to as a chameleon hash [69] demands $\mathsf{Equiv }$ to equivocate legitimate commitments generated by $\mathsf{Com }$.

Definition 3

(Homomorphic) A commitment scheme is homomorphic if for any correctly generated $ck$, the message, commitment and opening spaces are abelian groups with binary operations “$\cdot$,” “$\odot$” and “$\otimes$,” respectively, and for all $( msg , com , open )$ and $( msg ', com ', open ')$ valid with respect to $ck$, it holds that $1\leftarrow \mathsf{Vrf }( ck , com \cdot com ', msg \odot msg ', open \otimes open ')$.

2.3 Digital Signatures

Definition 4

(Digital Signature Scheme) A digital signature scheme $\mathsf{SIG }$ is a quadruple of efficient algorithms $(\mathsf{Setup }, \mathsf{Key }, \mathsf{Sign }, \mathsf{Vrf })$ such that

• $gk \leftarrow \mathsf{Setup }(1^\lambda )$ is a common-parameter generator that takes security parameter $\lambda$ and outputs a set of common parameters $gk$.

• $( vk , sk ) \leftarrow \mathsf{Key }( gk )$ is a key generation algorithm that takes common parameters $gk$ and generates a verification key $vk$ and a signing key $sk$. The verification key $vk$ defines the message space ${\mathcal {M}}$.

• $\sigma \leftarrow \mathsf{Sign }( sk , msg )$ is a signature-generation algorithm that computes a signature $\sigma$ for input message $msg \in {\mathcal {M}}$ by using signing key $sk$.

• $0/1 \leftarrow \mathsf{Vrf }( vk , msg ,\sigma )$ is a signature-verification algorithm that outputs 1 for acceptance or 0 for rejection.

We require the signature scheme to be correct, i.e., for any $( vk , sk )$ generated by $\mathsf{Key }$, any message $msg \in {\mathcal {M}}$ and any signature $\sigma$ output by $\mathsf{Sign }( sk , msg )$ the verification $\mathsf{Vrf }( vk , msg ,\sigma )$ outputs 1.

We use the standard notion of existential unforgeability against adaptive chosen-message attacks [52] (EUF-CMA for short), which says it is not possible to forge a signature on a previously unsigned message.

Definition 5

(Existential Unforgeability against Adaptive Chosen-Message Attacks) A signature scheme is existentially unforgeable against adaptive chosen-message attacks if for any probabilistic polynomial-time adversary ${{\mathcal {A}}}$

$$\begin{aligned} \Pr \left[ \begin{array}{l} gk \leftarrow \mathsf{Setup }(1^\lambda ); \ ( vk , sk ) \leftarrow \mathsf{Key }( gk )\\ (m^{\star }, \sigma ^{\star }) \leftarrow {{\mathcal {A}}}^{\mathsf{Sign }( sk ,\cdot )}( vk )\end{array}: \begin{array}{l}m^{\star } \not \in Q_m\\ 1 \leftarrow \mathsf{Vrf }( vk ,m^{\star }, \sigma ^{\star })\end{array} \right] \end{aligned}$$

is negligible, where $Q_m$ is the set of messages that were queried to the signing oracle $\mathsf{Sign }( sk ,\cdot )$.

By requiring $(m^{\star },\sigma ^{\star }) \not \in Q_{m,\sigma }$, where $Q_{m,\sigma }$ are the pairs of messages and signatures observed by $\mathsf{Sign }( sk ,\cdot )$, we obtain the notion of Strong EUF-CMA (denoted by ${\hbox {sEUF-CMA}}$ for short). This ensures that even if a message has been signed before, it is not possible to forge a new different signature on the message.

2.4 Bilinear Groups

We say ${\mathcal {G}}$ is a bilinear-group generator if on input security parameter $\lambda$ returns the description of a bilinear group $\Lambda =(p,{{\mathbb {G}}},\tilde{{{\mathbb {G}}}},{{\mathbb {G}}}_T,e,G,\tilde{G})\leftarrow {\mathcal {G}}(1^\lambda )$ with the following properties:

• ${{\mathbb {G}}},\tilde{{{\mathbb {G}}}}$ and ${{\mathbb {G}}}_T$ are groups of prime order $p$, whose bit-length is $\lambda$.

• $e:{{\mathbb {G}}}\times \tilde{{{\mathbb {G}}}}\rightarrow {{\mathbb {G}}}_T$ is a bilinear map, that is $e(U^a,\tilde{V}^b)=e(U,\tilde{V})^{ab}$ for all $U\in {{\mathbb {G}}},\tilde{V}\in \tilde{{{\mathbb {G}}}},a,b\in {{\mathbb {Z}}}_p$.

• $G$ and $\tilde{G}$ are uniformly chosen generators of ${{\mathbb {G}}}$ and $\tilde{{{\mathbb {G}}}}$, and $e(G,\tilde{G})$ generates ${{\mathbb {G}}}_T$.

• There are efficient algorithms for computing group operations, evaluating the bilinear map, comparing group elements and deciding membership of the groups. We refer to these as generic operations.

Galbraith et al. [51] distinguish between 3 types of bilinear-group generators. Type I groups have ${{\mathbb {G}}}=\tilde{{{\mathbb {G}}}}$ and are called symmetric bilinear groups. By ${\mathcal {G}}_{\mathsf{sym }}$, we denote a group generator that takes security parameter $\lambda$ and outputs a description of a symmetric bilinear group $\Lambda =(p,{{\mathbb {G}}},{{\mathbb {G}}}_T,e,G)$. Type II and Type III groups, which are referred to as asymmetric bilinear groups, have ${{\mathbb {G}}}\ne \tilde{{{\mathbb {G}}}}$, and we may sometimes write $\Lambda \leftarrow {\mathcal {G}}_{\mathsf{asym }}(1^\lambda )$ to emphasize when we are generating asymmetric bilinear groups. Type II groups have an efficiently computable homomorphism $\psi :\tilde{{{\mathbb {G}}}}\rightarrow {{\mathbb {G}}}$, while Type III groups do not have efficiently computable homomorphisms in either direction. When we need to explicitly discriminate $\Lambda$ in Type I, II and III, we write $\Lambda _{\mathsf{sym }}$, $\Lambda _{\mathsf{xdh }}$ and $\Lambda _{\mathsf{sxdh }}$, respectively.

The commitment and signature schemes in this work will have a common setup phase which generates common parameters $gk$. These will always consist of a description of a bilinear group $\Lambda \leftarrow {\mathcal {G}}(1^\lambda )$ and in some cases contain additional generators. This definitional approach means that many different structure-preserving protocols may use the same setup $gk$ and thus work over the same bilinear group, which is what makes them interoperable and easy to combine.

Note that in the symmetric case $\Lambda$ includes a generator $G$, and in the asymmetric case, it includes two generators $G$ and $\tilde{G}$. Some constructions and assumptions described for asymmetric bilinear groups can accommodate the symmetric case by considering ${{\mathbb {G}}}= \tilde{{{\mathbb {G}}}}$ and $G = \tilde{G}$. Some applications require $\tilde{G}\ne G$ in symmetric bilinear groups. In these cases, we pick a random generator, say $H$, and set $\tilde{G}= H$. A note will be given when such a treatment is necessary.

2.5 Assumptions

Our commitment and signature schemes rely on different assumptions regarding the bilinear groups we use. Most of the assumptions have reductions from the well-known decisional assumptions DDH and DLIN, but we will also rely on two new computational assumptions $q$-SFP and $q$-ADH-SDH, which we will describe later in the section. All assumptions are defined relative to a group generator. Therefore, every construction in the succeeding sections assumes that there exists a group generator for which relevant assumptions hold.

Assumption 1

(Decision Diffie–Hellman Assumption (DDH)) The decision Diffie–Hellman assumption holds in ${{\mathbb {G}}}$ relative to ${\mathcal {G}}_{\mathsf{asym }}$ if for all probabilistic polynomial-time ${{\mathcal {A}}}$

$$\begin{aligned} \left| \Pr \left[ \begin{array}{r}\Lambda \leftarrow {\mathcal {G}}_{\mathsf{asym }}(1^\lambda );a,b\leftarrow \mathbb {Z}_p:\\ 1\leftarrow {{\mathcal {A}}}(\Lambda ,G^a,G^b,G^{ab})\end{array}\right] - \Pr \left[ \begin{array}{r}\Lambda \leftarrow {\mathcal {G}}_{\mathsf{asym }}(1^\lambda );a,b,c\leftarrow \mathbb {Z}_p:\\ 1\leftarrow {{\mathcal {A}}}(\Lambda ,G^a,G^b,G^{c})\end{array}\right] \right| \end{aligned}$$

is negligible.

The decision Diffie–Hellman assumption in $\tilde{{{\mathbb {G}}}}$ is defined analogously. In the bilinear-group setting the decision Diffie–Hellman assumption in ${{\mathbb {G}}}$ (which we denote $\mathrm{DDH } _{{{\mathbb {G}}}}$) or in $\mathrm{DDH } _{\tilde{{{\mathbb {G}}}}}$ is sometimes referred to as the external Diffie–Hellman (XDH) assumption. The assumption that DDH holds in both ${{\mathbb {G}}}$ and $\tilde{{{\mathbb {G}}}}$ is sometimes referred to as the symmetric external Diffie–Hellman (SXDH) assumption. The DDH assumption cannot hold in symmetric bilinear groups, in which the decision linear assumption may be made instead.

Assumption 2

(Decision Linear Assumption (DLIN)) The decision linear assumption [23] holds in ${{\mathbb {G}}}$ relative to ${\mathcal {G}}$ if for all probabilistic polynomial-time ${{\mathcal {A}}}$

$$\begin{aligned} \left| \Pr \left[ \begin{array}{l}\Lambda \leftarrow {\mathcal {G}}(1^\lambda );a,b,r,s\leftarrow \mathbb {Z}_p:\\ 1\leftarrow {{\mathcal {A}}}(\Lambda ,G^a,G^b,G^{r},G^s,G^{ar+bs})\end{array}\right] - \Pr \left[ \begin{array}{c}\Lambda \leftarrow {\mathcal {G}}(1^\lambda );a,b,r,s,t\leftarrow \mathbb {Z}_p:\\ 1\leftarrow {{\mathcal {A}}}(\Lambda ,G^a,G^b,G^r,G^s,G^{t})\end{array}\right] \right| \end{aligned}$$

is negligible.

The 2-out-of-3 CDH assumption [70] states that given a tuple of group elements $(G,G^a,H)$, it is hard to output $(G^r,H^{ar})$ for an arbitrary $r\ne 0$. To break the Flexible CDH assumption [74], an adversary must additionally compute $G^{ar}$. We further weaken the assumption by defining a solution as $(G^r,G^{ar},H^r,H^{ar})$ and generalize it to asymmetric groups by letting $G\in {{\mathbb {G}}}$ and $H=\tilde{G}\in \tilde{{{\mathbb {G}}}}$ (whereas in symmetric groups, we let $H$ be an additional generator of ${{\mathbb {G}}}$ playing the role of $\tilde{G}$). The asymmetric weak flexible CDH is formalized as follows:

Assumption 3

(Asymmetric Weak Flexible CDH Assumption (AWF-CDH)) We say that the asymmetric weak flexible computational Diffie–Hellman assumption holds relative to ${\mathcal {G}}$ if for all probabilistic polynomial-time adversaries ${{\mathcal {A}}}$

$$\begin{aligned} \displaystyle \Pr \left[ \begin{array}{l}\Lambda \leftarrow {\mathcal {G}}(1^\lambda );\\ A \leftarrow {{\mathbb {G}}}^*;\\ (R,M,S,N)\leftarrow {{\mathcal {A}}}(\Lambda ,A)\end{array}:\begin{array}{l} (R,M,S,N) \in ({{\mathbb {G}}}^*)^2\times (\tilde{{{\mathbb {G}}}}^*)^2\\ e(A,S)=e(M,\tilde{G})\\ e(M,\tilde{G})=e(G,N)\\ e(R,\tilde{G})=e(G,S) \end{array} \right] \end{aligned}$$

(1)

is negligible.

Lemma 1

If $\mathrm{DDH } _{{{\mathbb {G}}}}$ holds relative to ${\mathcal {G}}$, then AWF-CDH holds relative to ${\mathcal {G}}$.

Proof

Let $(\Lambda ,G^a,G^b,G^c)$ be an instance of $\mathrm{DDH } _{{{\mathbb {G}}}}$. We have to decide whether $c=ab$. On input $(\Lambda ,G^a)$, a successful AWF-CDH adversary outputs $(G^r,G^{ra},\tilde{G}^r,\tilde{G}^{ra})$. We can thus check whether $e(G^c,\tilde{G}^r)=e(G^{ab},\tilde{G}^r)=e(G^b,\tilde{G}^{ra})$.$\square$

Assumption 4

(Double Pairing Assumption (DBP)) We say the double pairing assumption holds relative to ${\mathcal {G}}_{\mathsf{asym }}$ if for any probabilistic polynomial-time algorithm ${\mathcal {A}}$

$$\begin{aligned}&\Pr \big [\Lambda \leftarrow {\mathcal {G}}_{\mathsf{asym }}(1^\lambda ); G_z\leftarrow {{\mathbb {G}}}^* ; (\tilde{Z},\tilde{R})\leftarrow {\mathcal {A}}(\Lambda ,G_z):\\&\quad \quad \tilde{Z},\tilde{R}\!\in \! \tilde{{{\mathbb {G}}}}^* \text { and } 1\!=\!e(G_z,\tilde{Z})\; e(G,\tilde{R})\big ] \end{aligned}$$

is negligible.

Lemma 2

If $\mathrm{DDH } _{{\mathbb {G}}}$ holds relative to ${\mathcal {G}}_{\mathsf{asym }}$, then so does $\mathrm{DBP } _{{\mathbb {G}}}$ relative to ${\mathcal {G}}_{\mathsf{asym }}$.

Proof

Suppose that there is an adversary ${\mathcal {A}}$ that breaks the DBP assumption. Namely, ${\mathcal {A}}$ finds a pair $(\tilde{Z},\tilde{R})\ne (1,1)$ satisfying the equation $e(G_z,\tilde{Z})\,e(G,\tilde{R})=1$ for randomly chosen $G_z$ with more than negligible probability. We will construct an adversary ${\mathcal {B}}$ which breaks $\mathrm{DDH } _{{{\mathbb {G}}}}$ by using ${\mathcal {A}}$ as a black-box.

Given a $\mathrm{DDH } _{{{\mathbb {G}}}}$ challenge tuple $(\Lambda ,A,B,C)=(\Lambda ,G^a,G^b,G^c)$, algorithm ${\mathcal {B}}$ gives ${\mathcal {A}}$ an input $(\Lambda ,A)$. If ${\mathcal {A}}$ outputs $(\tilde{Z},\tilde{R})\ne (1,1)$ satisfying $e(G,\tilde{Z})\,e(A,\tilde{R})=1$, it is true that $\tilde{Z}=\tilde{R}^{-a}$. ${\mathcal {B}}$ outputs $1$ if $e(B,\tilde{Z})\ e(C,\tilde{R}) = 1$ and outputs 0, otherwise. This strategy is correct since $e(B,\tilde{Z})\, e(C,\tilde{R})=e(B,\tilde{R}^{-a})\, e(C,\tilde{R})=e(G,\tilde{R})^{c-ab}$ equals to 1 if and only if $c=ab \mod p$. Thus, ${\mathcal {B}}$ breaks $\mathrm{DDH } _{{{\mathbb {G}}}}$ if ${\mathcal {A}}$ breaks $\mathrm{DBP } _{{{\mathbb {G}}}}$.$\square$

We could consider a dual assumption of DBP by swapping ${{\mathbb {G}}}$ and $\tilde{{{\mathbb {G}}}}$. When we need to discriminate these assumptions, we call this assumption DBP in ${{\mathbb {G}}}$ (as it is implied by DDH in ${{\mathbb {G}}}$) and the dual assumption DBP in $\tilde{{{\mathbb {G}}}}$, and denote them as $\mathrm{DBP } _{{{\mathbb {G}}}}$ and $\mathrm{DBP } _{\tilde{{{\mathbb {G}}}}}$, respectively. Analogously to Lemma 2, $\mathrm{DBP } _{\tilde{{{\mathbb {G}}}}}$ holds if $\mathrm{DDH } _{\tilde{{{\mathbb {G}}}}}$ holds. Therefore, if DDH holds in both ${{\mathbb {G}}}$ and $\tilde{{{\mathbb {G}}}}$, then DBP holds in both ${{\mathbb {G}}}$ and $\tilde{{{\mathbb {G}}}}$.

Corollary 1

If SXDH holds relative to ${\mathcal {G}}$, then DBP holds in both ${{\mathbb {G}}}$ and $\tilde{{{\mathbb {G}}}}$ relative to ${\mathcal {G}}$.

DBP does not hold in symmetric bilinear groups and we will therefore also rely on the Simultaneous Double Pairing Assumption (SDP), which is plausible in both symmetric and asymmetric bilinear groups.

Assumption 5

(Simultaneous Double Pairing Assumption (SDP)) The simultaneous double pairing assumption SDP holds in ${{\mathbb {G}}}$ relative to ${\mathcal {G}}$ if for all probabilistic polynomial-time adversaries ${{\mathcal {A}}}$

$$\begin{aligned} \Pr \left[ \begin{array}{l}\Lambda \leftarrow {\mathcal {G}}(1^\lambda );\\ G_z,H_z,H_{u}\leftarrow {{\mathbb {G}}}^*;\\ (\tilde{Z},\tilde{R},\tilde{U})\leftarrow {{\mathcal {A}}}(\Lambda ,G_z,H_z,H_{u})\end{array}:\begin{array}{l} (\tilde{Z},\tilde{R},\tilde{U})\in (\tilde{{{\mathbb {G}}}}^*)^3 \\ 1=e(G_z,\tilde{Z})\, e(G,\tilde{R}) \\ 1 = e(H_z,\tilde{Z})\, e(H_{u},\tilde{U})\end{array} \right] \end{aligned}$$

is negligible.

The following lemma is proved in [38].

Lemma 3

If the DLIN assumption holds relative to a symmetric bilinear groups generator ${\mathcal {G}}_{\mathsf{sym }}$, then the SDP assumption holds relative to ${\mathcal {G}}_{\mathsf{sym }}$.

Assumption 6

(External Diffie–Hellman Inversion Assumption (XDHI)) The XDHI assumption holds relative to ${\mathcal {G}}$ if for all probabilistic polynomial-time adversaries ${{\mathcal {A}}}$

$$\begin{aligned} \Pr \left[ \Lambda \leftarrow {\mathcal {G}}(1^\lambda );\, a \leftarrow \mathbb {Z}_p^*;\, \tilde{H}\leftarrow \tilde{{{\mathbb {G}}}}^*;\, A \leftarrow {{\mathcal {A}}}(\Lambda ,\tilde{H}, \tilde{H}^a)\;:\;A=G^{1/a}\right] \end{aligned}$$

is negligible.

Assumption 7

(Co-Computational Diffie–Hellman Assumption (co-CDH)) The co-CDH assumption [25] holds relative to ${\mathcal {G}}$ if for all probabilistic polynomial-time adversaries ${{\mathcal {A}}}$

$$\begin{aligned} \Pr \left[ \Lambda \leftarrow {\mathcal {G}}(1^\lambda );\, a, b \leftarrow \mathbb {Z}_p^*;\, A \leftarrow {{\mathcal {A}}}(\Lambda , G^a, \tilde{G}^b)\;:\;A=G^{ab}\right] \end{aligned}$$

is negligible.

Depending on the type of the bilinear group $\Lambda$, the XDHI assumption is implied by standard assumptions, such as the computational Diffie–Hellman assumption (CDH), the co-Diffie–Hellman assumption (co-CDH) and the decisional Diffie–Hellman assumption in $\tilde{{{\mathbb {G}}}}$ ($\mathrm{DDH } _{\tilde{{{\mathbb {G}}}}}$), as follows. Note that, $\mathrm{CDH }$ is implied by $\mathrm{DLIN }$ in $\Lambda _{\mathsf{sym }}$ and $\mathrm{DDH } _{\tilde{{{\mathbb {G}}}}}$ is implied by SXDH in $\Lambda _{\mathsf{sxdh }}$.

Lemma 4

$\mathrm{CDH } \Rightarrow \mathrm{XDHI }$ for ${\mathcal {G}}_{\mathsf{sym }}$. $\mathrm{co-CDH } \Rightarrow \mathrm{XDHI }$ for ${\mathcal {G}}_{\mathsf{asym }}$. $\mathrm{DDH } _{\tilde{{{\mathbb {G}}}}} \Rightarrow \mathrm{XDHI }$ for ${\mathcal {G}}_{\mathsf{asym }}$.

Proof

Let ${\mathcal {A}}$ be an XDHI adversary with respect to ${\mathcal {G}}_{\mathsf{sym }}$ and let $\Lambda _{\mathsf{sym }}= (p, {{\mathbb {G}}}, {{\mathbb {G}}}_T, G, e) \leftarrow {\mathcal {G}}_{\mathsf{sym }}(1^\lambda )$. Note that $G$ is a uniformly chosen generator. Given a CDH instance $(\Lambda _{\mathsf{sym }}, G^\alpha , G^\beta )$, set $\Lambda _{\mathsf{sym }}' = (p, {{\mathbb {G}}}, {{\mathbb {G}}}_T, G^\alpha , e)$ and run ${{\mathcal {A}}}$ on the XDHI instance $(\Lambda _{\mathsf{sym }}', G^\beta , G)$. It outputs $G^{\alpha \beta }$, which is the solution to the CDH instance.

For the second implication, given an co-CDH instance $(\Lambda _{\mathsf{xdh }}, G^{\alpha }, \tilde{G}^{\beta }) \in {{\mathbb {G}}}^* \times \tilde{{{\mathbb {G}}}}^*$, choose $\tilde{G}' \leftarrow \tilde{{{\mathbb {G}}}}$, set $\Lambda _{\mathsf{xdh }}' = (p, {{\mathbb {G}}}, \tilde{{{\mathbb {G}}}}, {{\mathbb {G}}}_T, G^\alpha , \tilde{G}', e)$ and run ${{\mathcal {A}}}$ on input $(\Lambda _{\mathsf{xdh }}', \tilde{G}^\beta , \tilde{G})$. It outputs $G^{\alpha \beta }$, which is the solution to the co-CDH instance.

For the third implication, given an instance $(\Lambda _{\mathsf{sxdh }}, \tilde{G}^{\alpha }, \tilde{G}^{\beta }, \tilde{G}^{\gamma })$ of $\mathrm{DDH } _{\tilde{{{\mathbb {G}}}}}$, choose $\tilde{G}' \leftarrow \tilde{{{\mathbb {G}}}}$, set $\Lambda _{\mathsf{sxdh }}' = (p, {{\mathbb {G}}}, \tilde{{{\mathbb {G}}}}, {{\mathbb {G}}}_T, G, \tilde{G}', e)$ and run ${{\mathcal {A}}}$ on input $(\Lambda _{\mathsf{sxdh }},\tilde{G}^{\alpha }, \tilde{G})$. If successful, ${{\mathcal {A}}}$ outputs $G^{\alpha }$. Then, $\gamma = \alpha \beta$ can be tested by checking if $e(G^\alpha , \tilde{G}^{\beta }) = e(G, \tilde{G}^{\gamma })$ holds or not.$\square$

We wish to extend SDP in such a way that even if we are given some solutions, it should be hard to find another solution. Observe that given an answer to an instance of SDP, one can easily get more answers by exploiting the linearity of the relation to be satisfied. We eliminate this linearity by multiplying random pairings to both sides of the SDP equations. We call the added random pairing a flexible pairing since; on the one hand, it provides non-malleability in that solutions cannot be merged, and on the other hand, it can be easily randomized or combined with other solutions if their secret exponents are known.

Assumption 8

(Simultaneous Flexible Pairing Assumption ($q$-SFP)) Let ${\mathcal {G}}_{{\mathrm{SFP }}}$ denote an algorithm that takes a group description $\Lambda$ as input and generates parameters $P_{{\mathrm{SFP }}}:= (G_z,H_z,H_{u},A,\tilde{A},B,\tilde{B})$ where $G_z$, $H_z$, $H_{u}$ are random generators of ${{\mathbb {G}}}$, and $(A,\tilde{A})$, $(B,\tilde{B})$ are random elements in ${{\mathbb {G}}}\times \tilde{{{\mathbb {G}}}}$. For $\Lambda$ and $P_{{\mathrm{SFP }}}$, let ${\mathcal {I}}_{{\mathrm{SFP }}}$ denote the set of tuples ${I}_j=(\tilde{Z}_{j},\tilde{R}_{j},\tilde{U}_{j}, S_{ij},\tilde{T}_{ij},V_{ij},\tilde{W}_{ij}) \in \tilde{{{\mathbb {G}}}}^*\times \tilde{{{\mathbb {G}}}}\times \tilde{{{\mathbb {G}}}}\times {{\mathbb {G}}}\times \tilde{{{\mathbb {G}}}}\times {{\mathbb {G}}}\times \tilde{{{\mathbb {G}}}}$ that satisfy

$$\begin{aligned} e(A, \tilde{A})&= e(G_z,\tilde{Z}_{j})\; e(G,\tilde{R}_{j})\; e(S_{ij}, \tilde{T}_{ij}) \quad \text {and} \end{aligned}$$

(2)

$$\begin{aligned} e(B, \tilde{B})&= e(H_z,\tilde{Z}_{j})\; e(H_{u},\tilde{U}_{j})\; e(V_{ij}, \tilde{W}_{ij}). \end{aligned}$$

(3)

For $I_1,\dots ,I_q$, let $Z(I_1,\dots ,I_q)$ denote collection of $\tilde{Z}_j$ in $I_j$. We say the $q$-simultaneous flexible pairing assumption holds relative to ${\mathcal {G}}$ if for any probabilistic polynomial-time adversary ${{\mathcal {A}}}$

$$\begin{aligned} \Pr \left[ \begin{array}{l} \Lambda \leftarrow {\mathcal {G}}(1^\lambda ); P_{{\mathrm{SFP }}}\leftarrow {\mathcal {G}}_{{\mathrm{SFP }}}(\Lambda );\\ {I}_1,\ldots ,{I}_q\leftarrow {\mathcal {I}}_{{\mathrm{SFP }}}; \\ {I}^{\star }\leftarrow {{\mathcal {A}}}(\Lambda ,P_{{\mathrm{SFP }}},{I}_1,\ldots ,{I}_q)\end{array}: \begin{array}{l} I^{\star }\in {\mathcal {I}}_{{\mathrm{SFP }}}\\ Z(I^{\star }) \not \in Z({I}_1,\ldots ,{I}_q) \end{array} \right] \end{aligned}$$

is negligible.

Note that the definition deliberately makes the restriction $\tilde{Z}\in {{\mathbb {G}}}^*$, since $\tilde{Z}=1$ would make the problem easily solvable.

To show that the $q$-SFP assumption is plausible, we will now prove that it holds the generic group model where the adversary only uses the generic bilinear-group operations.

Theorem 1

For any generic algorithm ${\mathcal {A}}$, the probability that ${\mathcal {A}}$ breaks the $q$-SFP assumption with $\ell$ group operations and pairings is bounded by ${\mathcal {O}}(q^2 + \ell ^2)/p$.

Before proving the theorem, we discuss implications of the above bound. In the real computation, the group operation over two elements corresponds to addition of their indices and the pairing operation corresponds to their multiplication. In the generic group model, these indices are simulated by addition and multiplication over variables and formulas. Among the elements initially given to algorithm ${\mathcal {A}}$ there are independent random group elements whose indices are unknown. In the simulation, these unknown indices are treated as independent variables. A group element related to those elements is indexed by a formula that describes the relation. Executions of group operations and pairings are simulated by adding or multiplying the formulas associated with the elements given as inputs to the operations. Since different formulas are supposed to represent different group elements, simulation becomes inconsistent to the real computation if any two indices represented by different formulas evaluate to the same value when concrete random values are assigned to the variables. The probability of inconsistent simulation is therefore an upper bound to any generic algorithm.

If all the formulas are polynomials, the index of a new group element yielded by a generic operation is a polynomial in the variables. For polynomials of total degree less than $d$, the bound after $\ell$ group operations with $k$ initial group elements is given as ${\mathcal {O}}(d \cdot (\ell ^2+k^2))/p$ by Schwartz’s lemma [87, 88]. Consider the case of DL where the initially given group elements are $G$ and $G^x$. The above argument tells that the index formula is a polynomial of degree 1 and the bound is ${\mathcal {O}}(\ell ^2)/p$. In the case of SDH, the initial elements are $G, G^x, G^{x^2}, \dots , G^{x^q}$. Thus, the index formula will be a polynomial of degree $q$, and the bound is ${\mathcal {O}}(q \cdot (\ell ^2 + q^2))/p$. The loss factor of $q$ can be as huge as the number of signature issuing, and hence, the security of SDH is far from DL. On the other hand, as we show in the proof, the indices of the initial input to SFP can be represented by Laurent polynomials of form $\frac{y}{x}$ with a common variable $x$ of a small constant degree in the denominator. The formula in the numerator varies for elements, but they remain of degree 1. Accordingly, the index of a new group element is a Laurent polynomial of the same form. By offsetting the common denominator $x$ and applying Schwartz’s lemma to the resulting regular polynomial of degree 2, we have the bound of ${\mathcal {O}}(\ell ^2 + q^2)/p$, which is close to the optimal bound in DL.

Proof

Let us without loss of generality assume we are in the symmetric setting where ${{\mathbb {G}}}=\tilde{{{\mathbb {G}}}}$ and $G=\tilde{G}$. The symmetric setting gives the adversary more freedom, since it is not restricted to treat elements in ${{\mathbb {G}}}$ and elements in $\tilde{{{\mathbb {G}}}}$ separately, so proving the lemma for the symmetric case automatically yields a proof in the asymmetric case too.

Using the generic group operations, the adversary can compute $\tilde{Z},\tilde{R},S,\tilde{T},\tilde{U},V,\tilde{W}$ as linear combinations of the $8+7q$ elements $G$, $G_z$, $H_z$, $H_{u}$,$A,\tilde{A}$, $B,\tilde{B}$, $\{\tilde{Z}_{j},\tilde{R}_{j}, S_{ij},\tilde{T}_{ij},\tilde{U}_{j},V_{ij},\tilde{W}_{ij}\}_{j=1}^q$. Taking discrete logarithms of all the group elements with respect to base $G$, this means the adversary can compute $z,r,s,t,u,v,w$ as linear combination of $1$, $g_z,h_z,h_u,a,\tilde{a},b,\tilde{b},\{z_{j},r_{j}, s_{ij},t_{ij},u_{j},v_{ij},w_{ij}\}_{j=1}^q$, where

$$\begin{aligned} r_{j}=a\cdot \tilde{a}- g_z\cdot z_{j} - s_{j} \cdot t_{j},\quad \text {and}\textstyle \quad u_{j}= \frac{b\cdot \tilde{b}- h_z\cdot z_{j} - v_{j} \cdot w_{j}}{h_u}. \end{aligned}$$

We will first consider $z,r,s,t,u,v,w$ as formal Laurent polynomials in $\mathbb {Z}_p[g_z,h_z,h_u,$ $a,\tilde{a},b,\tilde{b},z_{1},\ldots ,w_{iq}]$. This means the adversary picks known coefficients $\zeta _*\in \mathbb {Z}_p$ and computes

$$\begin{aligned} z&= \zeta _{g_z}g_z+\zeta _{h_z}h_z+\zeta _{g_r}+\zeta _{h_u}h_u+\zeta _{a}a+\zeta _{\tilde{a}}\tilde{a}+\zeta _{b}b+\zeta _{\tilde{b}}\tilde{b}+\sum \limits _{j=1}^q\zeta _{z_{j}}z_{j} +\sum \limits _{j=1}^q\zeta _{s_{ij}}s_{ij}+\sum \limits _{j=1}^q\zeta _{t_{ij}}t_{ij} \\&+\sum \limits _{j=1}^q\zeta _{v_{ij}}v_{ij}\!+\!\sum \limits _{j=1}^q\zeta _{w_{ij}}w_{ij} \!+\!\sum \limits _{j=1}^q\zeta _{r_{j}}(a\cdot \tilde{a}- g_z\cdot z_{j} - s_{j} \cdot t_{j}) +\! \sum \limits _{j=1}^q\zeta _{u_{j}}\frac{b\cdot \tilde{b}- h_z\cdot z_{j} - v_{j} \cdot w_{j}}{h_u}. \end{aligned}$$

and constructs the Laurent polynomials $r,s,t,u,v,w$ in a similar way with coefficients labeled $\rho _*,\sigma _*,\tau _*,\mu _*$, etc., respectively.

Suppose the adversary’s Laurent polynomials satisfy the two verification equations

$$\begin{aligned} a\cdot \tilde{a}&= g_z\cdot z + r + s \cdot t \end{aligned}$$

(4)

$$\begin{aligned} b\cdot \tilde{b}&= h_z\cdot z + h_u\cdot u + v \cdot w. \end{aligned}$$

(5)

Let EQ3 be the equations obtained by substituting $z,r,s,t$ in (4) with corresponding Laurent polynomials. We will first show that EQ3 implies $\sigma _{r_{j}}=0$ for all $j$. Suppose for contradiction that $\sigma _{r_{i}}\ne 0$ for some $i$. The term $s_{i}^2t_{i}^2$ only appears in the product $s\cdot t$, so its coefficient $\sigma _{r_{i}}\tau _{r_{i}}$ must be 0. This means $\tau _{r_{i}}=0$. Looking at other terms, we see that most of the coefficients in $t$ are 0, the term $s_{i}t_{i}a$ for instance has coefficient $\sigma _{r_{i}}\tau _{a}$ and gives us $\tau _{a}=0$, and we get that $t=\tau _{g_z}g_z+\tau _{g_r}$. The coefficients of the $s_{j}t_{j}$ terms now give us $\rho _{r_{j}}+\sigma _{r_{j}}\tau _{g_r}=0$ for all $j$. Putting all this together, we see the right-hand side of EQ3 has coefficient $0$ for the $a\tilde{a}$ term. But the left hand side of EQ3 is $a\tilde{a}$ yielding a contradiction. We conclude $\sigma _{r_{j}}=0$ for all $j$ and by symmetry of $s$ and $t$, we also get that $\tau _{r_{j}}=0$ for all $j$.

If $\rho _{r_{i}}\ne 0$ for some $i$, we get without loss of generality from EQ3 that $\sigma _{s_{i}}\ne 0$ and $\tau _{t_{i}}\ne 0$. The coefficients of $s_{i}^2$ and $t_{i}^2$ in $s\cdot t$ have to be 0 since these terms do not appear in $g_z\cdot z$ or $r$, so we get $\sigma _{t_{i}}=0$ and $\tau _{s_{i}}=0$. Looking at coefficients for terms involving $s_{i}$ in EQ3, we see that most of them must have 0 coefficients. We therefore get $t=\tau _{g_z}g_z+\tau _{g_r}+\tau _{t_{i}}t_{i}$. Symmetrically, we get $s=\sigma _{g_z}g_z+\sigma _{g_r}+\sigma _{s_{i}}s_{i}$. The terms of $s_{j}t_{j}$ for $j\ne i$ in EQ3 now give us $\rho _{r_{j}}=0$ for $j\ne i$. Since the left-hand side of EQ3 has the term $a\tilde{a}$, we see $\rho _{r_{i}}=1$. The $g_zz_{i}$ terms now shows us that $\zeta _{z_{i}}=1$. Additional inspection of the different terms gives us $z=\zeta _{g_z}g_z+\zeta _{g_r}+z_{i}+\zeta _{s_{i}}s_{i}+\zeta _{t_{i}}t_{i}.$

We now consider the other possibility that $\rho _{r_{j}}$ is $0$ for all $j$. The term $a\tilde{a}$ gives us without loss of generality that $\sigma _{a}\ne 0$ and $\tau _{\tilde{a}}\ne 0$. The coefficients of $a^2$ and $\tilde{a}^2$ show us $\tau _{a}=0$ and $\sigma _{\tilde{a}}=0$. Inspecting the other terms, we get $t=\tau _{g_z}g_z+\tau _{g_r}+\tau _{\tilde{a}}\tilde{a}$ and $s=\sigma _{g_z}g_z+\sigma _{g_r}+\sigma _{a}a$. It then follows by looking at different terms that $z=\zeta _{g_z}g_z+\zeta _{g_r}+\zeta _{a}a+\zeta _{\tilde{a}}\tilde{a}.$

We have now deduced from (4) that $z=\zeta _{g_z}g_z+\zeta _{g_r}+\zeta _{a}a+\zeta _{\tilde{a}}\tilde{a}$ or $z=\zeta _{g_z}g_z+\zeta _{g_r}+z_{i}+\zeta _{s_{i}}s_{i}+\zeta _{t_{i}}t_{i}$ for some $i$. By symmetry, we get from (5) that $z=\zeta _{h_z}h_z+\zeta _{h_u}h_u+\zeta _{b}b+\zeta _{\tilde{b}}\tilde{b}$ or $z=\zeta _{h_z}h_z+\zeta _{h_u}h_u+z_{i}+\zeta _{v_{i}}v_{i}+\zeta _{w_{i}}w_{i}$ for some $i$. The equations can be consistent only if $z\in \{0,z_1,\ldots ,z_q\}$. Neither of those choices of $z$ would constitute a successful breach of the assumption, so we conclude that there are no formal Laurent polynomials the adversary can use to violate the assumption.

When instantiating the bilinear groups, we pick $g_z,h_z,h_u,z_{j}\leftarrow \mathbb {Z}_p^*$ and $a,\tilde{a},b,\tilde{b},$ $s_{j},t_{j},v_{j},w_{j}\leftarrow \mathbb {Z}_p$. In a typical run, the adversary would expect group elements corresponding to different Laurent polynomials to be different but there is some probability that this fails; when it fails, the adversary may be able to exploit it to break the assumption. The generic adversary’s probability of success can therefore be bounded by the chance that two different Laurent polynomials collide on random inputs in $\mathbb {Z}_p$.

Let $F$ and $F'$ be two different Laurent polynomials associated with elements in ${{\mathbb {G}}}$ computed by the adversary. By multiplying $F$ and $F'$ by $h_u$, we get two different degree 3 polynomials. The probability of having a collision is therefore bounded by $\frac{3}{p-1}$ according to Schwartz’s lemma [87]. Having initially $8 + 7 q$ elements, we get after $\ell _1$ group operations in ${{\mathbb {G}}}$ an upper bound of

$$\begin{aligned} \textstyle \left( {\begin{array}{c}8 + 7q+ \ell _1\\ 2\end{array}}\right) \cdot \frac{3}{p-1} \le \frac{{\mathcal {O}}((q+ \ell _1)^2)}{p} \end{aligned}$$

(6)

for Laurent polynomials for elements in ${{\mathbb {G}}}$ evaluating to the same value.

Using the pairing operation, the adversary gets Laurent polynomials for elements in ${{\mathbb {G}}}_T$ corresponding to products of Laurent polynomials for elements in ${{\mathbb {G}}}$. Multiplying by $h_u^2$, we get polynomials of degree at most $6$. The risk of having a collision after $\ell _T$ pairing operations and group operations in ${{\mathbb {G}}}_T$ is bounded by $\left( {\begin{array}{c}\ell _T\\ 2\end{array}}\right) \cdot \frac{6}{p-1} = \frac{{\mathcal {O}}(\ell _T^2)}{p}$. By setting $\ell = \ell _1 + \ell _T$, we simplify the sum of the upper bounds to $\frac{{\mathcal {O}}(q^2 + \ell ^2)}{p}$ as stated in Theorem 1.$\square$

Given an answer $(\tilde{Z},\tilde{R},\tilde{U})$ to the SDP problem (Assumption 5) then setting $(S, \tilde{T}, V, \tilde{W}) := (A, \tilde{A}, B, \tilde{B})$ results in a correct solution $(\tilde{Z},\tilde{R},\tilde{U},S,\tilde{T},V,\tilde{W})$ to the SFP problem. We thus obtain the following:

Lemma 5

If the $q$-SFP assumption (for arbitrary $q$) holds relative to ${\mathcal {G}}$, then the SDP assumption holds relative to ${\mathcal {G}}$.

Proof

Suppose that there exists an algorithm ${\mathcal {A}}$ that successfully finds a valid answer $(\tilde{Z}, \tilde{R}, \tilde{U})$ to SDP. We construct an algorithm that breaks SFP as follows. Given an SFP instance $(\Lambda , G_z, H_z, H_{u}, A, \tilde{A}, B, \tilde{B}, {I}_1, \dots , {I}_{q})$, input $(\Lambda ,G_z, H_z, H_{u})$ to ${\mathcal {A}}$. If ${\mathcal {A}}$ outputs $(\tilde{Z}^{\star }, \tilde{R}^{\star }, \tilde{U}^{\star })$ breaking the SDP instance, set $(S^{\star }, \tilde{T}^{\star }, V^{\star }, \tilde{W}^{\star }) := (A, \tilde{A}, B, \tilde{B})$ and output ${I}^{\star }=(\tilde{Z}^{\star },\tilde{R}^{\star },\tilde{U}^{\star },S^{\star },\tilde{T}^{\star },V^{\star },\tilde{W}^{\star })$.

Multiplying $1 = e(G_z,\tilde{Z}^{\star }), e(G_{r},\tilde{R}^{\star })$ to both sides of $e(A,\tilde{A}) = e(S^{\star },\tilde{T}^{\star })$ results in Eq. (2). Similarly, multiplying $1 = e(H_z,\tilde{Z}^{\star })\,e(H_{u},\tilde{U}^{\star })$ to both sides of $e(B,\tilde{B}) = e(V^{\star },\tilde{W}^{\star })$ results in Eq. (3). Thus, $I^{\star }$ satisfies the SFP equations. Since $(\tilde{Z}^{\star },\tilde{R}^{\star },\tilde{U}^{\star })$ is a valid answer to SDP, $\tilde{Z}^{\star } \ne 1$ holds. Since every $\tilde{Z}_j$ in $I_j$ is uniformly chosen and independent of $(G_z, H_z, H_{u}, A, \tilde{A}, B, \tilde{B})$, it is independent of the view of the adversary. Thus, $\tilde{Z}^{\star } = \tilde{Z}_j$ happens only with negligible probability for every $j\in \{1,\dots ,q\}$. Thus, $I^{\star }$ is a correct and valid answer to the $q$-SFP instance.$\square$

Our last assumption is a variant of the $q$-strong Diffie–Hellman (SDH) assumption [22]. In [48], it is shown that SDH implies hardness of the following two problems in bilinear groups:

• 1. Given $G,G^x$ and $q-1$ random pairs $(G^\frac{1}{x+c_i},c_i)$, output a new pair $(G^\frac{1}{x+c},c)$.

• 2. Given $G,K,G^x$ and, for random $c_i,v_i$: $\big ((K\cdot G^{v_i})^\frac{1}{x+c_i},c_i,v_i\big )_{i=1}^{q-1}$, output a new $((K\cdot G^{v})^\frac{1}{x+c},c,v)$.

Boyen and Waters [29] define the Hidden SDH assumption which states that the first problem is hard when the pairs are substituted with triples of the form $(G^{1/(x+c_i)},G^{c_i},H^{c_i})$, for a fixed generator $H$; the scalar $c_i$ is thus “hidden.” Analogously, we define a variant of the second problem by “hiding” the scalars $c_i$ and $v_i$, stating that given $F,G,H,K,G^x,H^x,\big ((K\!\cdot G^{v_i})^\frac{1}{x+ c_i}, F^{c_i}, H^{c_i}, G^{v_i}, H^{v_i} \big )_{i=1}^{q-1}$, it is hard to output a tuple $(A=(K\!\cdot G^{v})^\frac{1}{x+ c}, B=F^{c}, D=H^{c}, V=G^{v}, W=H^{v})$ with $(c,v) \ne (c_i,v_i)$ for all $i$. Due to the pairing, a tuple can still be effectively verified. The assumption holds in the generic group model for both asymmetric and symmetric groups, and we state it for the former.

Assumption 9

(Asymmetric Double Hidden Strong DH Assumption ($q$-ADH-SDH)) Let ${\mathcal {G}}_{{\mathrm{ADH-SDH }}}$ denote an algorithm that takes a group description $\Lambda$ as input and generates parameters $P_{{\mathrm{ADH-SDH }}}:= (F, K, X, \tilde{Y}) \in {{\mathbb {G}}}^3\times \tilde{{{\mathbb {G}}}}$ where $F$, $K$ and $X=G^x$ are random generators of ${{\mathbb {G}}}$, and $\tilde{Y}=\tilde{G}^x$.

For $\Lambda$ and $P_{{\mathrm{ADH-SDH }}}$, let ${\mathcal {I}}_{{\mathrm{ADH-SDH }}}$ denote the set of tuples ${I}_i=(A_i,B_i,\tilde{D}_i,V_i,\tilde{W}_i)\in {{\mathbb {G}}}^2\times \tilde{{{\mathbb {G}}}}\times {{\mathbb {G}}}\times \tilde{{{\mathbb {G}}}}$ that satisfy $\tilde{Y}\cdot \tilde{D}_i \ne 1$ and

$$\begin{aligned} e(A_i,\tilde{Y}\cdot \tilde{D}_i)&=e(K\cdot V_i,\tilde{G})&e(B_i,\tilde{G})&=e(F,\tilde{D}_i)&e(V_i,\tilde{G})&=e(G,\tilde{W}_i) \end{aligned}$$

(7)

We say the $q$-asymmetric double hidden strong Diffie–Hellman assumption holds relative to ${\mathcal {G}}$ if for any probabilistic polynomial-time adversary ${{\mathcal {A}}}$

$$\begin{aligned} \Pr \left[ \begin{array}{l} \Lambda \leftarrow {\mathcal {G}}(1^\lambda ); P_{{\mathrm{ADH-SDH }}}\leftarrow {\mathcal {G}}_{{\mathrm{ADH-SDH }}}(\Lambda );\\ {I}_1,\ldots ,{I}_{q-1}\leftarrow {\mathcal {I}}_{{\mathrm{ADH-SDH }}}; \\ {I}^{\star }\leftarrow {{\mathcal {A}}}(\Lambda ,P_{{\mathrm{ADH-SDH }}},{I}_1,\ldots ,{I}_q)\end{array}\ : \ I^{\star }\in {\mathcal {I}}_{{\mathrm{ADH-SDH }}}{\setminus }\{{I}_1,\ldots ,{I}_q\} \right] \end{aligned}$$

is negligible.

In symmetric bilinear groups (where ${{\mathbb {G}}}= \tilde{{{\mathbb {G}}}}$), we replace $\tilde{G}\in \tilde{{{\mathbb {G}}}}$ by a random generator $H\in {{\mathbb {G}}}$. We prove generic security of the assumption in symmetric groups, which yields a stronger result, as it implies security in asymmetric groups.

Theorem 2

The $q$-ADH-SDH assumption holds in generic bilinear groups when $q$ is a polynomial.

Proof

We prove the symmetric case, therefore every $\tilde{G}$ in the statement of Assumption 9 is replaced by a random generator $H$ of ${{\mathbb {G}}}$; that is, we prove that given $(p,{{\mathbb {G}}},{{\mathbb {G}}}_T,e,G)$ and $(F,K,H,X)\mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}{{\mathbb {G}}}^4$ and $Y:=H^{\log _G X}$, as well as $q-1$ tuples $(A_,B_i,D_i,V_i,W_i)$ satisfying

$$\begin{aligned} e(A_i,Y\cdot D_i)&=e(K\cdot V_i,H)&e(B_i,H)&=e(F, D_i)&e(V_i,H)&=e(G,W_i) \end{aligned}$$

(8)

it is hard to generate a new tuple $(A,B,D,V,W)$ satisfying the above.

We follow the approach of [22] in proving the generic security. Every element from ${{\mathbb {G}}}$ and ${{\mathbb {G}}}_T$ is represented by a random string, and the adversary has access to an oracle for group operations in ${{\mathbb {G}}}$ and ${{\mathbb {G}}}_T$ and pairings: Given the representation of two elements $A,A'\in {{\mathbb {G}}}$, the oracle responds with the representation of $A\cdot A'\in {{\mathbb {G}}}$, or $e(A,A')$ respectively, and analogously for $T,T'\in {{\mathbb {G}}}_T$. Internally, the simulator represents the elements as their logarithms relative to the group generator $G$ (and ${{\mathbb {G}}}_T$ elements relative to $e(G,G)$). When answering queries, it stores the symbolic representation of the returned element as an addition or multiplication of the polynomials for the queried elements. At the end, the simulator chooses random secret values and instantiates all stored polynomials. The simulation was perfect if no nonidentical polynomials yield the same value, which (due to Schwartz’s lemma [87], since the initial polynomials are of constant degrees and the adversary can only make polynomially many queries) is negligible in $\lambda$.

It remains to show that from a challenge the adversary cannot symbolically compute a new tuple satisfying (8). We represent every group element by its discrete logarithm (index) with respect to $G$. An ADH-SDH tuple ${I}_i$ that satisfies the equations in (8) can be written as

$$\begin{aligned} \big (A_{i}=(K\cdot G^{v_i})^{\frac{1}{x+c_i}},\,B_{i}=F^{c_i},\, D_{i}=H^{c_i},\,V_{i}=G^{v_i},\,W_{i}=H^{v_i}\big ) \end{aligned}$$

(9)

for some $c_i\in \mathbb {Z}_p{\setminus }\{-x\}$ and $v_i \in \mathbb {Z}_p$. Let a lower-case letter denote the index of the group elements denoted by the corresponding upper-case letter. A $q$-ADH-SDH instance is thus represented by the following rational fractions:

$$\begin{aligned} 1,\ f,\ h,\ k,\ x,\ y=xh,\ \big \{a_i={\textstyle \frac{k+v_i}{x+c_i}},\ b_i=c_if,\ d_i=c_ih,\ v_i,\ w_i=v_ih\big \}_{i=1}^{q-1} \end{aligned}$$

(10)

Let $(A^*,B^*,D^*,V^*,W^*)$ be a solution to this instance, that is, a tuple satisfying the equations in (8). Considering the logarithms of the ${{\mathbb {G}}}_T$-elements in these equations w.r.t. basis $e(G,G)$ yields

$$\begin{aligned} a^*(xh+d^*)&=(k+v^*)h&b^*h&=d^*f&v^*h&=w^* \end{aligned}$$

(11)

In a generic group, all the adversary can do is apply the group operation to the elements of its input. We will show that the only linear combinations $(a^*,b^*,d^*,v^*,w^*)$ of elements in (10) satisfying (11) are $(a^*=a_i={\textstyle \frac{k+v_i}{x+c_i}},b^*=b_i=c_if,d^*=d_i=c_ih,v^*=v_i,w^*=w_i=v_ih)$ for some $i$. A quintuple from the instance is, however, not a valid solution, meaning a generic adversary cannot break the assumption. We make the following ansatz for $a^*$:

$$\begin{aligned} a^*&= \alpha +\alpha _f f+\alpha _h\, h+\alpha _k\, k+\alpha _x\,x+\alpha _y\,xh \\&\quad +\,\textstyle \sum \alpha _{a,i}\frac{k+v_i}{x+c_i}+\sum \alpha _{b,i}\,c_if+\sum \alpha _{d,i}\,c_ih+\sum \alpha _{v,i}\,v_i+\sum \alpha _{w,i}\,v_ih .\end{aligned}$$

Analogously, we write $b^*,d^*,v^*$ and $w^*$, whose coefficients we denote by $\beta$, $\delta$, $\mu$ and $\omega$, respectively.

By the last equation of (11) we have that for any $v^*$ the adversary forms, it has to provide $w^*=v^*h$ as well. We can therefore limit the elements used for $v^*$ to those of which their product with $h$ is also given: $1,x$ and $v_i$ (for all $i$). This yields

Similarly, plugging in the ansätze for $b^*$ and $d^*$ in the second equation of (11) and equating coefficients eliminates all of the coefficients except those for $fh$ (which yields $\beta _f=\delta _h=:\gamma$) and those for $c_ifh$ (which yields $\beta _{b,i}=\delta _{d,i}=:\gamma _i$), for all $i$. We have thus

We substitute $a^*,d^*,v^*$ by their ansätze in the first equation of (11); that is, $~a^*(xh+d^*)-v^*h=kh$. Since every term contains $h$, for convenience we omit one $h$ per term (i.e., we symbolically “divide” the equation by $h$). The first equation of (11) can thus be written as

$$\begin{aligned}&\alpha x+\alpha _f fx+\alpha _h\, hx+\alpha _k\, kx+\alpha _x\,xx+\alpha _y\,xhx \\&\quad +\,\textstyle \sum \alpha _{a,i}\frac{(k+v_i)x}{x+c_i}+\sum \alpha _{b,i}\,c_ifx+\sum \alpha _{d,i}\,c_ihx+\sum \alpha _{v,i}\,v_ix+\sum \alpha _{w,i}\,v_ihx \\&\quad +\, \alpha \gamma +\alpha _f\gamma \, f+\alpha _h\gamma \, h+\alpha _k\gamma \, k+\alpha _x\gamma \,x+\alpha _y\gamma \,xh \\&\quad +\,\textstyle \sum \alpha _{a,i}\gamma \,\frac{k+v_i}{x+c_i}+\sum \alpha _{b,i}\gamma \,c_if+\sum \alpha _{d,i}\gamma \,c_ih+\sum \alpha _{v,i}\gamma \,v_i+\sum \alpha _{w,i}\gamma \,v_ih \\&\quad +\, {\textstyle \sum }\alpha \gamma _{i}\,c_i+{\textstyle \sum }\alpha _f\gamma _i fc_i+{\textstyle \sum }\alpha _h\gamma _i\, hc_i+{\textstyle \sum }\alpha _k\gamma _i\, kc_i+{\textstyle \sum }\alpha _x\gamma _i\,xc_i+{\textstyle \sum }\alpha _y\gamma _i\,xhc_i\\&\quad +\,\textstyle {\textstyle \sum }{\textstyle \sum }\alpha _{a,i}\gamma _j\frac{(k+v_i)c_j}{x+c_i}+{\textstyle \sum }{\textstyle \sum }\alpha _{b,i}\gamma _j\,c_ifc_j\\&\quad +\,{\textstyle \sum }{\textstyle \sum }\alpha _{d,i}\gamma _j\,c_ihc_j+{\textstyle \sum }{\textstyle \sum }\alpha _{v,i}\gamma _j\,v_ic_j+{\textstyle \sum }{\textstyle \sum }\alpha _{w,i}\gamma _j\,v_ihc_j \\&\quad -\, \mu +\mu _x x+{\textstyle \sum }\mu _{v,i}v_i = k ,\end{aligned}$$

which after regrouping yields

$$\begin{aligned}&(\alpha \gamma -\mu )\ 1\ +\ (\alpha _f\gamma )\ f\ +\ (\alpha _h\gamma )\ h\ +\ (\alpha +\alpha _x\gamma -\mu _x)\ x+(\alpha _h+\alpha _y\gamma )\ xh\ \end{aligned}$$

(12a)

$$\begin{aligned}&+{\textstyle \sum }\ (\alpha _{a,i}\gamma )\ \frac{k+v_i}{x+c_i}\ +\ {\textstyle \sum }\ (\alpha _{b,i}\gamma +\alpha _f\gamma _{i})\ c_if\ +\ {\textstyle \sum }\ (\alpha _{d,i}\gamma +\alpha _h\gamma _{i})\ c_ih\ + {\textstyle \sum }(\alpha _{w,i}\gamma )\ v_ih\ \end{aligned}$$

(12b)

$$\begin{aligned}&+(\alpha _f)\ xf\ +\ (\alpha _k)\ xk\ +\ (\alpha _x)\ x^2 + (\alpha _y)\ x^2h+ {\textstyle \sum }\ (\alpha _{d,i}+\alpha _y\gamma _{i})\ c_ixh\ +\ {\textstyle \sum }\, (\alpha _{b,i})\, c_ixf\, \end{aligned}$$

(12c)

$$\begin{aligned}&+ {\textstyle \sum }\ (\alpha _{v,i})\ v_ix\ +\ {\textstyle \sum }\ (\alpha _{w,i})\ v_ixh\ + {\textstyle \sum }\, (\alpha \gamma _{i})\, c_i\, +{\textstyle \sum }\, (\alpha _k\gamma _{i})\, c_ik\,+\, {\textstyle \sum }\,(\alpha _x\gamma _{i})\,xc_i \end{aligned}$$

(12d)

$$\begin{aligned}&+{\textstyle \sum }{\textstyle \sum }\, (\alpha _{b,i}\gamma _{j})\, c_ic_jf\ +\ {\textstyle \sum }{\textstyle \sum }\, (\alpha _{d,i}\gamma _{j})\, c_ic_jh +\ {\textstyle \sum }{\textstyle \sum }\, (\alpha _{v,i}\gamma _{j})\, v_ic_j\ +\ {\textstyle \sum }{\textstyle \sum }\, (\alpha _{w,i}\gamma _{j})\, v_ic_jh\ \end{aligned}$$

(12e)

$$\begin{aligned}&+\underbrace{(\alpha _k\gamma )}_{=:\lambda _k}\,k\,+\, {\textstyle \sum }\, \underbrace{(\alpha _{v,i}\gamma -\mu _{v,i})}_{=:\lambda _{v,i}}\,v_i\,+\,{\textstyle \sum }\, \underbrace{(\alpha _{a,i})}_{=:\lambda _{xa,i}}\, \frac{x(k+v_i)}{x+c_i}+ {\textstyle \sum }{\textstyle \sum }\, \underbrace{(\alpha _{a,i}\gamma _{j})}_{=:\lambda _{ca,i,j}}\, \frac{c_j(k+v_i)}{x+c_i}\ =\ k. \end{aligned}$$

(12f)

To do straightforward comparison of coefficients, we would have to multiply the equation by $\prod _{i=1}^{q-1}(x+c_i)$ first. For the sake of presentation, we keep the fractions and instead introduce new equations for the cases where a linear combination leads to a fraction that cancels down.

Now, comparison of coefficients of the two sides of the above equation shows that all coefficients in lines (12a)–(12e) must be 0, whereas for the last line we have a different situation: Adding $\frac{x(k+v_i)}{x+c_i}$ and $\frac{c_i(k+v_i)}{x+c_i}$ reduces to $k+v_i$ (but this is the only combination that reduces); we have thus

$$\begin{aligned}&\text {for all }i:\lambda _{xa,i}=\lambda _{ca,i,i}&\text {for all }i\ne j:\lambda _{ca,i,j}=0 \end{aligned}$$

(13)

$$\begin{aligned}&\text {coefficient of} k:\quad {\textstyle \sum }\lambda _{xa,i}+\lambda _k=1&\text {coefficient of}\,\, v_i:\quad \lambda _{xa,i}+\lambda _{v,i}=0 \end{aligned}$$

(14)

We now solve the equations “all coefficients in Lines (12a) to (12e) equal 0,” and Eqs. (13) and (14) for the values $\big (\alpha ,\alpha _f, \alpha _h,\alpha _k,\alpha _x,\alpha _y,\gamma ,\mu ,\mu _x,\{\alpha _{a,i},\alpha _{b,i}, \alpha _{d,i},$ $\alpha _{v,i},\alpha _{w,i},\gamma _{i},\mu _{v,i}\}\big )$.

The first four terms and the last term in Line (12c) and the first two terms in Line (12d) immediately yield: $\alpha _f=\alpha _k=\alpha _x=\alpha _y=\alpha _{b,i}=\alpha _{v,i}=\alpha _{w,i}=0$ for all $i$. Now $\alpha _y=0$ implies $\alpha _h=0$ by the last term in (12a), and moreover, $\alpha _{d,i}=0$ for all $i$ by the fifth term in (12c). Plugging in these values, the only equations different from “$0=0$” are the following:

$$\begin{aligned} \alpha \,\gamma -\mu&= 0&\qquad \qquad \alpha - \mu _x&= 0 \end{aligned}$$

(15)

$$\begin{aligned} \alpha _{a,i}\,\gamma&= 0 \ \ (\forall i)&\qquad \qquad \alpha \,\gamma _{i}&= 0 \ \ (\forall i) \end{aligned}$$

(16)

$$\begin{aligned} \alpha _{a,i}(1-\gamma _{i})&= 0 \ \ (\forall i)&\qquad \qquad \alpha _{a,i}\,\gamma _{j}&= 0 \ \ (\forall i\ne j) \end{aligned}$$

(17)

$$\begin{aligned} \textstyle \sum \limits _{i=1}^{q-1} \alpha _{a,i}&= 1&\qquad \qquad \alpha _{a,i} - \mu _{v,i}&= 0 \ \ (\forall i) \end{aligned}$$

(18)

where the second equation in (15), denoted by “(15.2)”, follows from the fourth term in (12a) and $\alpha _x=0$. (16.1) and (16.2) follow from the first term in (12b) and the third term in (12d), respectively. Equations (17) are the equations in (13); those in (18) are the ones from (14) taking into account that $\alpha _k=0$ and $\alpha _{v,i}=0$ for all $i$. The variables not yet proved to be 0 are $\alpha ,\gamma ,\mu ,\mu _x,\alpha _{a,i},\gamma _{i}$ and $\mu _{v,i}$ for $1\le i\le q-1$.

We first show that there exists $i^*\in \{1,\ldots ,q-1\}$ such that $\alpha _{a,j}=0$ for all $j\ne i^*$: Assume there exist $i\ne j$ such that $\alpha _{a,i}\ne 0$ and $\alpha _{a,j}\ne 0$; then by (17.1), we have $\gamma _{i}=\gamma _{j}=1$, which contradicts (17.2).

This result implies the following: by (18.1), we have $\alpha _{a,i^*}=1$, and by (17.1), we have $\gamma _{i^*}=1$, whereas for all $j\ne i^*$: $\gamma _{j}=0$ by (17.2). We have thus shown that $\alpha _{a,i^*}=\gamma _{i^*}=1$ and $\alpha _{a,j}=\gamma _{j}=0$ for all $j\ne i^*$.

This now implies $\alpha =0$ (by 16.2), and thus, $\mu =\mu _x=0$ by [(15.1) and (15.2), respectively]. Moreover, $\gamma =0$ (by 16.1) and for all $i$: $\alpha _{a,i}=\mu _{v,i}$ (by 18.2). The only nonzero variables are thus $\alpha _{a,i^*}=\gamma _{i^*}=\mu _{v,i^*}=1$.

Plugging in our results in the ansätze for $a^*,b^*,d^*,v^*$ and $w^*$, we proved that there exists $i^*\in \{1,\ldots ,q-1\}$ such that $a^*=\frac{k+v_{i^*}}{x+c_{i^*}}$, $b^*=c_{i^*}f$, $d^*=c_{i^*}h$, $v^*=v_{i^*}$ and $w^*=v_{i^*}h$. This means that the only tuples $(A^*,B^*,D^*,V^*,W^*)$ satisfying (8) and being generically constructible from a ADH-SDH instance are the tuples from that instance, which concludes our proof of generic security of ADH-SDH.$\square$

2.6 The Groth–Sahai Proof System for Pairing-Product Equations

The Groth–Sahai (GS) proof system [59] gives efficient non-interactive witness-indistinguishable (NIWI) proofs and non-interactive zero-knowledge (NIZK) proofs for languages that can be described as sets of satisfiable equations, each of which falls in one of the following categories: pairing-product equations, multi-exponentiation equations and general arithmetic gates. The GS proof system can be instantiated under different assumption: for instance in the asymmetric setting under the SXDH assumption, which says DDH holds in both ${{\mathbb {G}}}$ and $\tilde{{{\mathbb {G}}}}$ and in the symmetric setting under the DLIN assumption.

In GS proofs, there are two types of common reference string (CRS), which are computationally indistinguishable. One type is called “real” and gives perfect soundness and allows extraction of the group elements of a witness given a secret extraction key that is set up together with the CRS. The second type is called “simulated” and yields perfectly witness-indistinguishable proofs, which are also zero knowledge for some types of equations. When proving a statement, described as a set of equations, one first commits to the witness components and then produces elements for each equation that prove the corresponding committed values satisfy the equation.

Of the types of equations the GS proof system supports, we are mainly interested in pairing-product equations over variables $X_1,\ldots ,X_m\in {{\mathbb {G}}}$ and $\tilde{Y}_1,\ldots ,\tilde{Y}_n\in \tilde{{{\mathbb {G}}}}$:

$$\begin{aligned} \textstyle \prod \limits _{i=1}^n e(A_i,\tilde{Y}_i)\; \prod \limits _{i=1}^m e(X_i, \tilde{B}_i)\; \prod \limits _{i=1}^m\prod \limits _{j=1}^n e(X_i,\tilde{Y}_j)^{c_{i,j}} \;=\; T , \end{aligned}$$

where $\{A_i\}_{i=1}^n \in {{\mathbb {G}}}^n$, $\{\tilde{B}_i\}_{i=1}^m \in \tilde{{{\mathbb {G}}}}^m$, $\{c_{i,j}\}_{i=1,j=1}^{\;m,\;\;n}\in \mathbb {Z}_p$, and $T\in {{\mathbb {G}}}_T$ are public constants. When the equations involve variables only in one of the groups, we get simpler, one-sided equations $\prod _{i=1}^n e(A_i,\tilde{Y}_i)=T$ or $\prod _{i=1}^m e(X_i,\tilde{B}_i)=T$, which also yield more efficient proofs.

In the SXDH instantiation, a commitment to a group element consists of two group elements and a proof for a pairing-product equation costs 8 group elements. In the symmetric DLIN instantiation, a commitment consists of 3 group elements and a proof consists of 9 group elements. For linear pairing-product equations, the size of a proof drops to 2 and 3 group elements in the SXDH and the DLIN settings, respectively.

The GS proof system is witness indistinguishable when $T \in {{\mathbb {G}}}_T$ is an element in the target group without some particular structure. If for each equation $T=1$, possibly after some rewriting of equations, the GS proof system becomes zero knowledge.

Note that in this context the word proof can denominate either “proof of satisfiability” or language membership (which thus includes the commitments) or mean a proof that the content of some given commitments satisfies a given equation. We adopt the latter diction and say proof of knowledge when we include the commitments. Please refer to [59] for further details.

2.7 Pairing-Randomization Techniques

We introduce techniques that randomize elements in a pairing or a pairing product without changing their value in ${{\mathbb {G}}}_T$. Not all of them are used in this paper, but they do have applications, e.g., [7].

• Inner Randomization $(X',Y') \leftarrow \mathsf{Rand }(X,Y)$: A pairing $A = e(X, Y) \ne 1$ is randomized as follows. Choose $\gamma \leftarrow \mathbb {Z}_p^*$ and let $(X', Y') =( X^\gamma , Y^{1/\gamma })$. It then holds that $(X', Y')$ distributes uniformly over ${{\mathbb {G}}}\times \tilde{{{\mathbb {G}}}}$ under the condition of $A = e(X', Y')$. If $A=1$, then first flip a coin and pick $e(1,1)$ with probability $1/(2p-1)$. Otherwise, select $X'\ne 1$ uniformly, and output either $e(1,X')$ or $e(X',1)$ with probability $1/2$.

• Sequential Randomization $\{X'_i,Y'_i\}_{i=1}^{{k}} \leftarrow \mathsf{RandSeq }(\{X_i,Y_i\}_{i=1}^{{k}})$: A pairing product $A = e(X_1, Y_1) \cdots e(X_{k}, Y_{k})$ is randomized into $A = e(X'_1, Y'_1) \cdots e(X'_{k}, Y'_{k})$ as follows: Pick $(\gamma _1, \dots , \gamma _{k-1}) \leftarrow \mathbb {Z}_p^{{k}-1}$. We begin with randomizing the first pairing using the second pairing as follows. First, verify that $Y_1 \ne 1$ and $X_2 \ne 1$. If $Y_1 = 1$, replace the first pairing $e(X_1, 1)$ with $e(1, Y_1)$ with a new random $Y_1 (\ne 1)$. The case of $X_2 = 1$ is handled the same way. Then, multiply $1 = e(X_2^{-\gamma _1}, Y_1)\, e(X_2, Y_1^{\gamma _1})$ to both sides of the formula. We thus obtain

  $$\begin{aligned} A = e(X_1 X_2^{-\gamma _1}, Y_1)\, e(X_2, Y_1^{\gamma _1} Y_2)\, e(X_3, Y_3) \cdots e(X_{k}, Y_{k}). \end{aligned}$$

  (19)

  Next, we randomize the second pairing using the third one. As before, if $Y_1^{\gamma _1} Y_2=1$ or $X_3=1$, replace them with random values. Then, multiply $1 = e(X_3^{-\gamma _2}, Y_1^{\gamma _1} Y_2)$ $e(X_3, (Y_1^{\gamma _1} Y_2)^{\gamma _2})$. We thus have

  $$\begin{aligned} A = e(X_1 X_2^{-\gamma _1}, Y_1)\, e(X_2 X_3^{-\gamma _2}, Y_1^{\gamma _1} Y_2)\, e(X_3, (Y_1^{\gamma _1} Y_2)^{\gamma _2} Y_3) \cdots e(X_{k}, Y_{k}). \end{aligned}$$

  (20)

  This continues up to the $({k}-1)$-th pairing. When done, the value of the $i$-th pairing distributes uniformly in ${{\mathbb {G}}}_T$ due to the uniform choice of $\gamma _i$. The $k$-th pairing follows the distribution determined by $A$ and the preceding ${k}-1$ pairings. Finally, process every pairing by the inner randomization.

• Extension $\{X'_i,Y'_i\}_{i=1}^{{k}'} \leftarrow \mathsf{Extend }(\{X_i,Y_i\}_{i=1}^{{k}})$: For ${k}' \ge {k}$, a pairing product $A = e(X_1, Y_1) \cdots e(X_{k}, Y_{k})$ is randomized to $A = e(X'_1, Y'_1) \cdots e(X'_{{k}'}, Y'_{{k}'})$ as follows: For $i\in [{k},{k}']$, let $X_i = 1$ and $Y_i = 1$. Then, execute $\{X'_i,Y'_i\}_{i=1}^{{k}'} \leftarrow \mathsf{RandSeq }(\{X_i,Y_i\}_{i=1}^{{k}'})$ and output $\{X'_i,Y'_i\}_{i=1}^{{k}'}$.

• One-side Randomization $\{X'_i\}_{i=1}^{{k}} \leftarrow \mathsf{RandOneSide }(\{G_i,X_i\}_{i=1}^{{k}})$: This algorithm works only in the symmetric setting $\Lambda _{\mathsf{sym }}$. Let $G_i$ be an element in ${{\mathbb {G}}}^*$. A pairing product $A = e(G_1, X_1) \cdots e(G_k, X_k)$ is randomized into $A = e(G_1, X'_1)\cdots e(G_k, X'_k)$ as follows. Pick $(\gamma _1, \dots , \gamma _{{k}-1}) \leftarrow \mathbb {Z}_p^{{k}-1}$ and multiply $1 = e(G_1, G_2^{\gamma _1})\, e(G_2, G_1^{-\gamma _1})$ to both sides of the formula. We thus obtain

  $$\begin{aligned} A = e(G_1, X_1 G_2^{\gamma _1})\, e(G_2, X_2 G_1^{-\gamma _1})\, e(G_3, X_3) \cdots e(G_{k}, X_{k}). \end{aligned}$$

  (21)

  Next, multiply $1 = e(G_2, G_3^{\gamma _2})\, e(G_3, G_2^{-\gamma _2})$, which yields

  $$\begin{aligned} A = e(G_1, X_1 G_2^{\gamma _1})\, e(G_2, X_2 G_1^{-\gamma _1} G_3^{\gamma _2})\, e(G_3, X_3 G_2^{-\gamma _2}) \cdots e(G_{k}, X_{k}). \end{aligned}$$

  (22)

  Continue until $\gamma _{{k}-1}$, so we eventually have $A = e(G_1, X'_1) \cdots e(G_k, X'_k)$. Observe that every $X'_i$ for $i=1,\dots ,{k}-1$ is distributed uniformly in ${{\mathbb {G}}}$ due to the uniform multiplicative factor $G_{i+1}^{\gamma _i}$. In the ${k}$-th pairing, $X'_k$ follows the distribution determined by $A$ and the preceding ${k}-1$ pairings. Thus, $(X'_1,\dots , X'_{k})$ is uniform over ${{\mathbb {G}}}^{k}$ conditioned on being evaluated to $A$.

Note that the algorithms yield uniform elements and thus may include pairings that evaluate to $1_{{{\mathbb {G}}}_T}$. If this is not preferable, it can be avoided by repeating that particular step once again excluding the bad randomness.

3 Homomorphic Trapdoor Commitments

Homomorphic trapdoor commitments are used in a number of contexts, in particular as a building block in zero-knowledge proofs. An example of a frequently used scheme is that of Pedersen [83] that can be used to commit to elements from the field $\mathbb {Z}_p$.

Our goal in this section is to construct homomorphic trapdoor commitment schemes for group elements. We will construct both strict structure-preserving commitments where both messages, commitments and openings are elements of the source groups ${{\mathbb {G}}}, \tilde{{{\mathbb {G}}}}$ and relaxed structure-preserving commitments where we allow the commitments to contain elements from the target group ${{\mathbb {G}}}_T$.

In [9], it is shown that when committing with source-group elements, the size of the commitment cannot be smaller than the size of the input message. The strict structure-preserving commitments therefore grow linearly with the number of group elements in the messages. To contrast this result, we also show that in the relaxed structure-preserving setting it is possible to get constant-size commitments for messages containing many group elements.

Table 1 summarizes the performance of structure-preserving homomorphic trapdoor commitment schemes from this section and the existing ones from [9, 38].

Table 1 Summary of homomorphic trapdoor commitments

3.1 Commitments Using Target-Group Elements

This section includes two homomorphic trapdoor commitment schemes whose commitments consist of elements in ${{\mathbb {G}}}_T$. The first scheme, $\mathsf{HTC{1} }$, works in both symmetric and asymmetric groups and can be seen as an optimization of the scheme we first presented in [56] with a simpler assumption. The second scheme, $\mathsf{HTC{2} }$, only works in the asymmetric setting in exchange of gaining efficiency.

Both schemes can be used to commit to $k$ group elements in $\tilde{{{\mathbb {G}}}}$ at once. It is inspired by the Pedersen commitment scheme, but uses pairings instead of exponentiations. The use of the pairing means that we commit to source-group elements, but the final commitment is a group element in the target group.

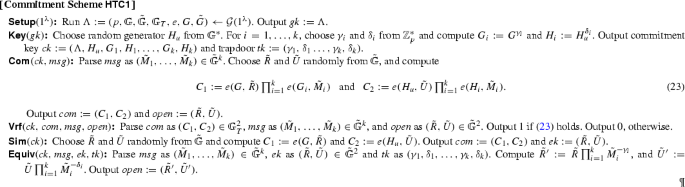
Theorem 3

$\mathsf{HTC{1} }$ is a homomorphic trapdoor commitment scheme. It is perfectly trapdoor and computationally binding if the SDP assumption holds in ${{\mathbb {G}}}$ relative to ${\mathcal {G}}$.

Proof

Correctness trivially holds by construction.

To see that the scheme is homomorphic, observe that

$$\begin{aligned} \textstyle&\textstyle \left( e(G, \tilde{R}) \prod \limits _{i=1}^{{k}} e(G_i, \tilde{M}_i)\right) \!\! \left( e(G, \tilde{R}') \prod \limits _{i=1}^{{k}} e(G_i, \tilde{M}'_i)\right) =\textstyle e(G, \tilde{R}\cdot \tilde{R}') \prod \limits _{i=1}^{{k}} e(G_i, \tilde{M}_i \cdot \tilde{M}'_i)\\ \textstyle&\textstyle \left( e(H_{u}, \tilde{U}) \prod \limits _{i=1}^{{k}} e(H_i, \tilde{M}_i)\right) \, \left( e(H_{u}, \tilde{U}') \prod \limits _{i=1}^{{k}} e(H_i, \tilde{M}'_i)\right) =\textstyle e(H_{u}, \tilde{U}\cdot \tilde{U}') \prod _{i=1}^{{k}} e(H_i, \tilde{M}_i \cdot \tilde{M}'_i) \end{aligned}$$

This means $(C_1 C'_1, C_2 C'_2)$ is a valid commitment to $(\tilde{M}_1 \tilde{M}'_1,\cdots ,\tilde{M}_k \tilde{M}'_k)$ that can be opened with $(\tilde{R}\tilde{R}', \tilde{U}\tilde{U}')$.

The commitment scheme is perfectly hiding because the components $e(G_{r},\tilde{R})$ and $e(H_{u},\tilde{U})$ make $C_1$ and $C_2$ uniformly random regardless of the message. The scheme is also perfectly trapdoor. To see this, observe that for any $(\tilde{M}_1,\dots ,\tilde{M}_k)$ and any $(C_1,C_2,\tilde{R},\tilde{U})$ and $(\tilde{R}', \tilde{U}')$ legitimately generated by $\mathsf{HTC{1} }.\mathsf{Sim }$ and $\mathsf{HTC{1} } \mathsf{.Equiv }$, respectively, and it holds that

$$\begin{aligned} \textstyle e(G,\tilde{R}')\prod \limits _{i=1}^{k} e(G_i,\tilde{M}_i)&=\textstyle e(G,\tilde{R}\prod \limits _{i=1}^{k}\tilde{M}_i^{-\gamma _i})\prod \limits _{i=1}^{k} e(G_i,\tilde{M}_i) = e(G, \tilde{R}) = C_1, \text { and}\\ \textstyle e(H_{u},\tilde{U}')\prod \limits _{i=1}^{k} e(H_i,\tilde{M}_i)&= \textstyle e(H_{u},\tilde{U}\prod \limits _{i=1}^{k}\tilde{M}_i^{-\delta _i})\prod \limits _{i=1}^{k} e(H_i,\tilde{M}_i) = e(H_{u}, \tilde{U}) = C_2. \end{aligned}$$

Thus, $\mathsf{HTC{1} }.\mathsf{Vrf }$ accepts $(\tilde{M}_1,\dots ,\tilde{M}_k)$ and $(\tilde{R}',\tilde{U}')$ as a correct opening for $(C_1,C_2)$. Moreover, since $C_1,C_2$ are uniformly random and the commitments and messages uniquely determine the openings, real commitments and openings have the same probability distribution as do simulated commitments and trapdoor openings.

Finally, we will show that $\mathsf{HTC{1} }$ is computationally binding. Suppose that there exists an adversary that successfully opens a commitment to two distinct messages. We show that one can break SDP by using such an adversary. Given an SDP challenge $(\Lambda , H_{u}, G_z, H_z)$, do as follows.

• Set $G_i:=G_z^{\chi _i} G^{\gamma _i}$ and $H_i:= H_z^{\chi _i} H_{u}^{\delta _i}$ for $i=1,\dots ,{k}$. Abort if $G_i=1$ or $H_i=1$ for any $i$. Otherwise, run the adversary on $ck = (\Lambda ,H_{u},G_1,H_1,\ldots ,G_k,H_k)$.

• Given two openings $(\tilde{M}_1,\dots ,\tilde{M}_k, \tilde{R}, \tilde{U})$ and $(\tilde{M}'_1,\dots ,\tilde{M}'_k, \tilde{R}', \tilde{U}')$ from the adversary that yield the same commitment $(C_1,C_2)$, compute

  $$\begin{aligned} \textstyle \tilde{Z}^{\star } := \prod \limits _{i=1}^{{k}} \Big (\frac{\tilde{M}_i}{^{\!\!\!\!\!}{\tilde{M'_i}}}\Big )^{\chi _i}, \quad \tilde{R}^{\star } := \frac{\tilde{R}}{^{\!\!\!\!\!}{\tilde{R}'}} \prod \limits _{i=1}^{{k}} \Big (\frac{\tilde{M}_i}{^{\!\!\!\!\!}{\tilde{M}'_i}}\Big )^{\gamma _i}, \quad \tilde{U}^{\star } := \frac{\tilde{U}}{^{\!\!\!\!\!}{\tilde{U}'}} \prod \limits _{i=1}^{{k}} \Big (\frac{\tilde{M}_i}{^{\!\!\!\!\!}{\tilde{M}'_i}} \Big )^{\delta _i}. \end{aligned}$$

  (24)

• Output $(\tilde{Z}^{\star }, \tilde{R}^{\star }, \tilde{U}^{\star })$.

The key generation step aborts with probability at most $2{k}/p$ that is negligible. Then, since the openings fulfills (23), we have

$$\begin{aligned}\textstyle 1&= \textstyle e\Big (G, \frac{\tilde{R}}{^{\!\!\!\!\!}{\tilde{R}'}}\Big ) \prod e\Big (G_i, \frac{\tilde{M}_i}{^{\!\!\!\!\!}{\tilde{M}'_i}}\Big ) = e\Big (G_z, \prod \limits _{i=1}^{{k}} \Big (\frac{\tilde{M}_i}{^{\!\!\!\!\!}{\tilde{M}'_i}}\Big )^{\chi _i}\Big ) \, e\Big (G, \frac{\tilde{R}}{^{\!\!\!\!\!}{\tilde{R}'}} \prod \limits _{i=1}^{{k}} \Big (\frac{\tilde{M}_i}{^{\!\!\!\!\!}{\tilde{M}'_i}}\Big )^{\gamma _i}\Big )\\&= e(G_z, \tilde{Z}^{\star })\, e(G, \tilde{R}^{\star }), \text { and}\\ 1&=\textstyle e\Big (H_{u}, \frac{\tilde{U}}{^{\!\!\!\!\!}{\tilde{U}'}}\Big ) \prod e\Big (H_i, \frac{\tilde{M}_i}{^{\!\!\!\!\!}{\tilde{M}'_i}}\Big ) = e\Big (H_z, \prod \limits _{i=1}^{{k}} \Big (\frac{\tilde{M}_i}{^{\!\!\!\!\!}{\tilde{M}'_i}}\Big )^{\chi _i}\Big ) \, e\Big (H_{u}, \frac{\tilde{U}}{^{\!\!\!\!\!}{\tilde{U}'}} \prod \limits _{i=1}^{{k}} \Big (\frac{\tilde{M}_i}{^{\!\!\!\!\!}{\tilde{M}'_i}}\Big )^{\delta _i}\Big )\\&= e(H_z, \tilde{Z}^{\star })\, e(H_{u}, \tilde{U}^{\star }). \end{aligned}$$

But $\vec {\tilde{M}} \ne \vec {\tilde{M}}'$, so there exists $i$ such that $\tilde{M}_i/\tilde{M}'_i\ne 1$. Also, $\chi _i$ is independent from the view of the adversary. That is, for every choice of $\chi _i$, there exist corresponding $\gamma _i$ and $\delta _i$ that give the same $G_i$ and $H_i$. Therefore, $\tilde{Z}^{\star }= \prod _i (\tilde{M}_i/\tilde{M}'_i)^{\chi _i} \ne 1$ with overwhelming probability and $\tilde{R}^{\star }, \tilde{U}^{\star } \ne 1$ holds automatically. Thus, $(\tilde{Z}^{\star }, \tilde{R}^{\star }, \tilde{U}^{\star })$ is a valid answer to the instance of SDP.$\square$

In asymmetric bilinear groups, we can deploy keys and messages in different groups that cannot map each other. As a result, we can construct more efficient scheme $\mathsf{HTC{2} }$ that works only in asymmetric bilinear groups.

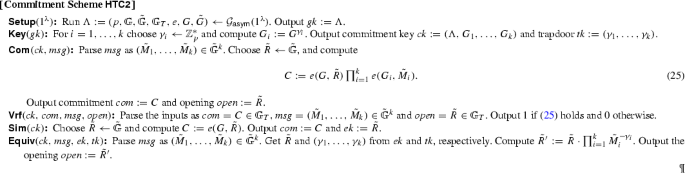
To commit to messages in ${{\mathbb {G}}}$, one can construct a “dual” scheme by interchanging the role of ${{\mathbb {G}}}$ and $\tilde{{{\mathbb {G}}}}$ in the above construction.

Theorem 4

$\mathsf{HTC{2} }$ is a homomorphic trapdoor commitment scheme. It is perfectly trapdoor and computationally binding if the DBP assumption holds in ${{\mathbb {G}}}$ relative to ${\mathcal {G}}_{\mathsf{asym }}$.

Proof

Correctness can be verified by inspection.

To see the commitment scheme is homomorphic, observe

$$\begin{aligned} \textstyle \Big (e(G, \tilde{R}) \prod \limits _{i=1}^{{k}} e(G_i, \tilde{M}_i)\Big )\, \Big (e(G, \tilde{R}') \prod \limits _{i=1}^{{k}} e(G_i, \tilde{M}'_i)\Big ) =e(G, \tilde{R}\cdot \tilde{R}') \prod \limits _{i=1}^{{k}} e(G_i, \tilde{M}_i \cdot \tilde{M}'_i). \end{aligned}$$

The commitment scheme is perfectly hiding because the randomization, $e(G,R)$, makes the commitment a uniformly random target-group element irrespective of the message. Furthermore, it is perfectly trapdoor because a simulated commitment is also a uniformly random target-group element and conditioned on a message and commitment (25) uniquely determines the opening.

To prove the commitment scheme is computationally binding, consider an adversary ${{\mathcal {A}}}$ that has not negligible probability of opening a commitment to two different messages. We will use it to construct an adversary ${\mathcal {B}}$ that breaks the DBP assumption.

${\mathcal {B}}$ gets as input a DBP challenge $(\Lambda ,G_z)$ and wants to find $\tilde{Z}^*,\tilde{R}^*\in \tilde{{{\mathbb {G}}}}^*$ such that $1=e(G_z,\tilde{Z}^*)\, e(G,\tilde{R}^*)$. ${\mathcal {B}}$ sets $G_i:=G_z^{\chi _i}G^{\gamma _i}$ with random $\chi _i,\gamma _i\leftarrow \mathbb {Z}_p$ for $i=1,\dots ,{k}$. ${\mathcal {B}}$ aborts if $G_i=1$ happens for any $i$, but it happens only with negligible probability. It then runs ${{\mathcal {A}}}$ on $ck = (\Lambda ,G_1,\ldots ,G_{k})$. If ${{\mathcal {A}}}$ returns two different messages and openings $(\tilde{M}_1,\dots ,\tilde{M}_k, \tilde{R})$ and $(\tilde{M}'_1,\dots ,\tilde{M}'_k, \tilde{R}')$ of the same commitment $C$ then ${\mathcal {B}}$ computes

$$\begin{aligned} \textstyle \tilde{Z}^* := \prod \limits _{i=1}^{{k}} \Big (\frac{\tilde{M}_i}{^{\!\!\!\!\!}{\tilde{M}'_i}}\Big )^{\chi _i} , \quad \tilde{R}^* := \frac{\tilde{R}}{^{\!\!\!\!\!}{\tilde{R}'}} \prod \limits _{i=1}^{{k}} \Big (\frac{\tilde{M}_i}{^{\!\!\!\!\!}{\tilde{M}'_i}}\Big )^{\gamma _i}. \end{aligned}$$

(26)

Since $C=e(G,\tilde{R})\prod _{i=1}^{{k}}e(G_i,\tilde{M}_i)=e(G,\tilde{R}')\prod _{i=1}^{{k}}e(G_i,\tilde{M}_i')$, the output satisfies $1=e(G_z,\tilde{Z}^*)\, e(G,\tilde{R}^*)$. Each $\chi _i$ value in $G_i=G_z^{\chi _i}G^{\gamma _i}$ is perfectly hidden by the random $G^{\gamma _i}$ component, so there is only a $\frac{1}{p}$ chance of $\tilde{Z}^*=1$. This gives ${\mathcal {B}}$ a solution to its DBP challenge.$\square$

As mentioned in the introduction, the length-reducing schemes in this section are useful in reducing the size of zero-knowledge arguments. In [58], $\mathsf{HTC{2} }$ is used to make commitments to group elements that themselves are Pedersen commitments. Pedersen commitments allow the commitment to multiple values $m_1,\ldots ,m_n\in {{\mathbb {Z}}}_p$ as $\tilde{G}^t\prod _{i=1}^n\tilde{G}_i^{m_i}$. We can use our length-reducing commitment schemes to commit to $k$ Pedersen commitments at once. Since our commitment schemes are homomorphic and the Pedersen commitment scheme is homomorphic, their combination is also homomorphic. We therefore get a homomorphic trapdoor commitment scheme to $nk$ elements from ${{\mathbb {Z}}}_p$. In contrast to the Pedersen commitment scheme, however, the public key of our scheme is only ${\mathcal {O}}(n+k)$ group elements. This means that both commitments and keys are much smaller than the number of messages $nk$.

3.2 Commitments Using Source-Group Elements

We will now show that it is also possible to make strict structure-preserving commitment to tuples of group elements. This means the commitments themselves should also consist of source-group elements. We will do this by modifying $\mathsf{HTC{1} }$ in the symmetric setting such that instead of publishing a commitment in ${{\mathbb {G}}}_T$, we publish the message and opening in randomized form. The randomization is done by applying the one-sided randomization $\mathsf{RandOneSide }$ from Sect. 2.7.

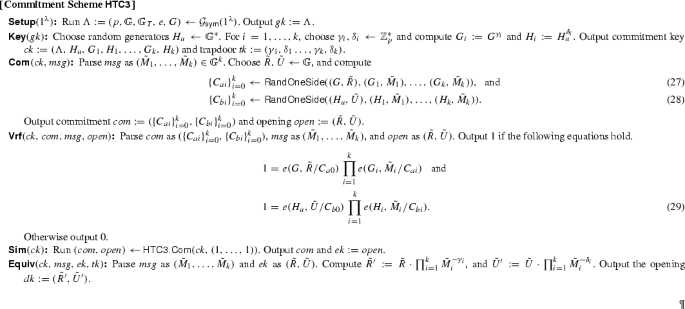
Theorem 5

$\mathsf{HTC{3} }$ is a homomorphic trapdoor commitment scheme. It is perfectly trapdoor and computationally binding if the SDP assumption holds relative to ${\mathcal {G}}_{\mathsf{sym }}$.

Proof

Since $\mathsf{RandOneSide }$ preserves the value of the pairing product, we have

$$\begin{aligned} \textstyle e(G,C_{a0})\prod \limits _{i=1}^{{k}} e(G_i,C_{ai})&=\textstyle e(G,\tilde{R}) \prod \limits _{i=1}^{{k}}e(G_i,\tilde{M}_i) \end{aligned}$$

(30)

$$\begin{aligned} \textstyle e(H_{u},C_{a0})\prod \limits _{i=1}^{{k}} e(H_i,C_{ai})&=\textstyle e(H_{u},\tilde{U}) \prod \limits _{i=1}^{{k}}e(H_i,\tilde{M}_i), \end{aligned}$$

(31)

which means the commitment scheme is correct.

We will now show the commitment scheme is homomorphic. Observe that

$$\begin{aligned}&\textstyle e(G,C_{a0}\cdot C_{a0}')\prod \limits _{i=1}^{{k}} e(G_i,C_{ai}\cdot C_{ai}')\\&\quad =\textstyle \Big (e(G,C_{a0})\prod \limits _{i=1}^{{k}} e(G_i,C_{ai})\Big ) \Big (e(G,C_{a0}')\prod \limits _{i=1}^{{k}} e(G_i,C_{ai}')\Big )\\&\quad =\textstyle \Big (e(G,\tilde{R}) \prod \limits _{i=1}^{{k}}e(G_i,\tilde{M}_i)\Big ) \Big (e(G,\tilde{R}') \prod \limits _{i=1}^{{k}}e(G_i,\tilde{M}'_i)\Big )\\&\quad =\textstyle e(G,\tilde{R}\cdot \tilde{R}') \prod \limits _{i=1}^{{k}}e(G_i,\tilde{M}_i\cdot \tilde{M}'_i), \end{aligned}$$

and a similar statement holds for the $C_{bi}$ values.

This means $com :=(\{C_{ai}C_{ai}'\}_{i=0}^{k}, \{C_{bi}C_{bi}'\}_{i=0}^{k})$ is a commitment to $msg :=(\tilde{M}_1\tilde{M}_1',$ $\cdots , \tilde{M}_k \tilde{M}'_k)$ with opening $open :=(\tilde{R}\tilde{R}', \tilde{U}\tilde{U}')$.

To see the commitment scheme is perfectly hiding, observe that regardless of the message, the commitment is a set of $2k+2$ uniformly random elements in ${{\mathbb {G}}}$.

The perfect trapdoor property and the computational binding under the SDP assumption carry over directly from the proof of Theorem 3 since the messages and openings are identical to those of $\mathsf{HTC{1} }$.$\square$

3.3 Committing to Messages in $\mathbb {Z}_p$

Though not structure-preserving, schemes to commit to elements in $\mathbb {Z}_p$ are often useful and needed in applications. The following scheme, $\mathsf{HTC{4} }$, resembles the commitment schemes in the literature studying NIZK over bilinear groups, e.g., [4, 59]. We present the scheme with a formal treatment.

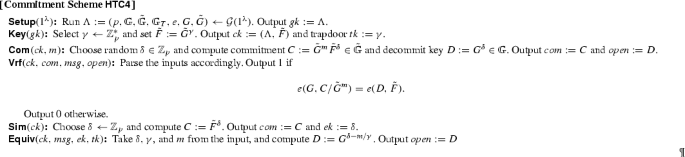
Theorem 6

Commitment scheme $\mathsf{HTC{4} }$ is a homomorphic trapdoor commitment scheme. It is perfectly hiding and computationally binding if the XDHI assumption holds for ${\mathcal {G}}$.

Proof

Correctness follows since $e(G, C/\tilde{G}^m) = e(G, \tilde{F}^\delta ) = e(G^\delta ,\tilde{F}) = e(D,\tilde{F})$. It is additively homomorphic since the following holds

$$\begin{aligned} e(G, C\cdot C'/\tilde{G}^{m+m'})&= e\big (G, (\tilde{G}^m \tilde{F}^\delta )\cdot (\tilde{G}^{m'} \tilde{F}^{\delta '})/\tilde{G}^{m+m'}\big )\\&= e(G^{\delta } \cdot G^{\delta '}, \tilde{F}) = e(D\cdot D',\tilde{F}). \end{aligned}$$

The perfect hiding property holds from the fact that, for any $C \in \tilde{{{\mathbb {G}}}}$, for every $m \in \mathbb {Z}_p$ there exists a single consistent $\delta \in \mathbb {Z}_p$.

The binding property is proven by showing a reduction to $\mathrm{XDHI }$. Given an instance of $\mathrm{XDHI }$, $(\Lambda ,\tilde{H},\tilde{H}^a)$, compose $\Lambda '$ from $\Lambda$ by replacing $\tilde{G}$ in $\Lambda$ with $\tilde{H}$ and set $\tilde{F}= \tilde{H}^a$. Suppose that an adversary is given $ck = (\Lambda ', \tilde{F})$ and outputs a commitment $c$ correctly opened to $(m,D)$ and $(m',D')$ for $m \ne m'$. Then, $e(G, C/\tilde{G}^{m}) = e(D,\tilde{F})$ and $e(G, C/\tilde{G}^{m'}) = e(D',\tilde{F})$ hold. By dividing both sides of the equations, we have $e(G,\tilde{G}^{m-m'}) = e(D'/D, \tilde{F}) = e(D'/D, \tilde{H}^a).$ Thus by computing $(D'/D)^{1/m-m'} (=G^{1/a})$, we have a correct answer to the XDHI instance.

The equivocation is correct because

$$\begin{aligned} e(D,\tilde{F}) = e(G^{\delta -m/\gamma }, \tilde{F}) = e(G, \tilde{G}^{-m} \tilde{F}^{\delta }) = e(G, C/\tilde{G}^{m}). \end{aligned}$$

And it is perfect because commitment $C$ generated by $\mathsf{Sim }$ distributes uniformly over $\tilde{{{\mathbb {G}}}}$ as well as those by $\mathsf{Com }$. Thus, the scheme has the trapdoor property.$\square$

4 One-Time Signature Schemes

This section presents two structure-preserving one-time signature schemes. The constructions are based on the trapdoor commitment schemes in Sect. 3. Mohassel [79] presented generic conversions from chameleon hash schemes to one-time signature schemes. Their conversion can start from trapdoor commitment schemes. In this section, we present one-time signature schemes achieving better security and efficiency than the generic ones.

4.1 Construction in General Setting

The first scheme, OTS1, is based on the trapdoor commitment scheme HTC1 from Sect. 3.1. Compared to $\mathsf{HTC{1} }$, it uses one extra random element to handle the one-time signing query and avoids target-group elements by representing them with pairings of random source-group elements.

The scheme is mainly designed for symmetric groups (as we show more efficient scheme in asymmetric groups), but it works also for asymmetric groups with unilateral messages belonging to $\tilde{{{\mathbb {G}}}}$.

Let $msg :=(M_1,\dots ,M_{k}) \in \tilde{{{\mathbb {G}}}}^{{k}}$ be a message to be signed. Parameter ${k}$ determines the length of a message.

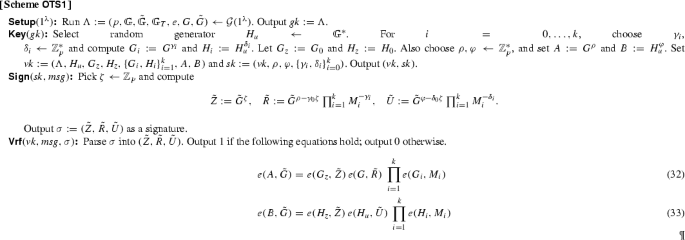
Theorem 7

$\mathsf{OTS{1} }$ is a one-time signature scheme that is strongly unforgeable against one-time chosen-message attacks if SDP holds for ${\mathcal {G}}$.

Proof

Syntactical consistency and correctness are verified by inspection. We focus on showing strong unforgeability. Suppose that there is a successful adversary, ${{\mathcal {A}}}$. We construct a reduction algorithm to SDP. Let $\Lambda :=(p, {{\mathbb {G}}},\tilde{{{\mathbb {G}}}},{{\mathbb {G}}}_T,e,G,\tilde{G})$ and $(G_z, H_z, H_{u})$ be an instance of SDP.

Adversary ${{\mathcal {A}}}$ is given public key $vk$ and then a one-time signature $\sigma$ for message $msg$ of its choice. It eventually outputs a valid forgery $(\sigma ^{\dagger }, msg ^{\dagger })$. To run ${{\mathcal {A}}}$ properly, the reduction algorithm simulates the public key and a one-time signature as follows.

• Simulating $vk$: Use given $\Lambda$ for $gk$ and $(G_z, H_z, H_{u})$ for the generators of the same name. For $i=1,\dots ,{k}$, choose $\chi _i$, $\gamma _i$, $\delta _i$ $\leftarrow$ $\mathbb {Z}_p$ and compute $G_i :=G_z^{\chi _i}G^{\gamma _i}$ and $H_i :=H_z^{\chi _i} H_{u}^{\delta _i}$. Also choose $\zeta , \rho , \varphi \leftarrow \mathbb {Z}_p$, and set $A:=G_z^{\zeta } G^{\rho }$ and $B:=H_z^{\zeta } H_{u}^{\varphi }$. Abort if any of $G_i$, $H_i$, $A$ and $B$ equals $1$. Send $vk :=(\Lambda , H_{u}, G_z, H_z, \{G_i, H_i\}_{i=1}^{{k}}, A, B)$ to ${{\mathcal {A}}}$.

• Simulating $\sigma$: On receiving $msg = (M_0,\dots ,M_{k})$, compute

  $$\begin{aligned} \textstyle \tilde{Z}:=\tilde{G}^{\zeta } \prod \limits _{i=1}^{{k}} M_i^{-\chi _i},\quad \tilde{R}:=\tilde{G}^{\rho } \prod \limits _{i=1}^{{k}} M_i^{-\gamma _i},\quad \tilde{U}:=\tilde{G}^{\varphi } \prod \limits _{i=1}^{{k}} M_i^{-\delta _i}. \end{aligned}$$

  Return $\sigma :=(\tilde{Z},\tilde{R},\tilde{U})$ to ${{\mathcal {A}}}$.

Simulation is perfect except for the case it aborts in the key generation, which happens only with negligible probability. Given output $(\tilde{Z}^{\dagger },\tilde{R}^{\dagger },\tilde{U}^{\dagger })$ and $(M^{\dagger }_1,\dots ,M^{\dagger }_{k})$ from ${{\mathcal {A}}}$, the reduction algorithm computes

$$\begin{aligned} \textstyle \tilde{Z}^{\star } :=\Big (\frac{\tilde{Z}^{\dagger }}{\tilde{Z}^{}}\Big ) \prod \limits _{i=1}^{{k}} {\Big (\frac{M^{\dagger }_i}{M_i}\Big )}^{\chi _i}, \quad \tilde{R}^{\star } :=\Big (\frac{\tilde{R}^{\dagger }}{\tilde{R}}\Big ) \prod \limits _{i=1}^{{k}} {\Big (\frac{M^{\dagger }_i}{M_i}\Big )}^{\gamma _i}, \quad \tilde{U}^{\star } :=\Big (\frac{\tilde{U}^{\dagger }}{\tilde{U}}\Big ) \prod \limits _{i=1}^{{k}} {\Big (\frac{M^{\dagger }_i}{M_i}\Big )}^{\delta _i}. \end{aligned}$$

(34)

Then output $(\tilde{Z}^{\star }, \tilde{R}^{\star }, \tilde{U}^{\star })$ as an answer to the instance of SDP. This completes the description of the reduction algorithm.

The simulation yields the view that distributes statistically close to the one in the real execution. The negligible error occurs when random coins are chosen so that one or more elements in $vk$ happen to be $1$. Thus, we can expect that ${{\mathcal {A}}}$ remains successful in the simulation.

Next, we show the correctness of the output of the reduction. By dividing both sides of (32) with respect to $(\tilde{Z}^{\star }, \tilde{R}^{\star }, \tilde{U}^{\star })$ and $(\tilde{Z},\tilde{R},\tilde{U})$, we have

$$\begin{aligned} 1&=\textstyle e\Big (G_z, \frac{\tilde{Z}^{\dagger }}{\tilde{Z}^{}}\Big )\, e\Big (G, \frac{\tilde{R}^{\dagger }}{\tilde{R}^{}}\Big )\, \prod \limits _{i=1}^{{k}}e\Big (G_i, \frac{M^{\dagger }_i}{M_i}\Big )\\&=\textstyle e\Big (G_z, \frac{\tilde{Z}^{\dagger }}{\tilde{Z}^{}} \prod \limits _{i=1}^{{k}} {\Big (\frac{M^{\dagger }_i}{M_i}\Big )}^{\chi _i}\Big )\, e\Big (G, \frac{\tilde{R}^{\dagger }}{\tilde{R}^{}} \prod \limits _{i=1}^{{k}} {\Big (\frac{M^{\dagger }_i}{M_i}\Big )}^{\gamma _i}\Big ) \ =\ e(G_z, \tilde{Z}^{\star })\,e(G, \tilde{R}^{\star }). \end{aligned}$$

Similarly, with respect to (33), we have

$$\begin{aligned} 1&=\textstyle e\Big (H_z, \frac{\tilde{Z}^{\dagger }}{\tilde{Z}^{}}\Big )\, e\Big (H_{u}, \frac{\tilde{U}^{\dagger }}{\tilde{U}^{}}\Big )\, \prod \limits _{i=1}^{{k}}e\Big (h_i, \frac{M^{\dagger }_i}{M_i}\Big )\\&=\textstyle e\Big (H_z, \frac{\tilde{Z}^{\dagger }}{\tilde{Z}^{}} \prod \limits _{i=1}^{{k}} {\Big (\frac{M^{\dagger }_i}{M_i}\Big )}^{\chi _i}\Big )\, e\Big (H_{u}, \frac{\tilde{U}^{\dagger }}{\tilde{U}^{}} \prod \limits _{i=1}^{{k}} {\Big (\frac{M^{\dagger }_i}{M_i}\Big )}^{\delta _i}\Big ) \ =\ e(H_z, \tilde{Z}^{\star })\,e(H_{u}, \tilde{U}^{\star }). \end{aligned}$$

Hence, $(\tilde{Z}^{\star }, \tilde{R}^{\star }, \tilde{U}^{\star })$ is a correct answer to the SDP instance.

It remains to show that $\tilde{Z}^{\star } \ne 1$.

We first consider the case of $(M_1,\dots ,M_k) = (M^{\dagger }_1,\dots ,M^{\dagger }_k)$. In this case, $(\tilde{Z}^{\dagger }, \tilde{R}^{\dagger },$ $\tilde{U}^{\dagger }) \ne (\tilde{Z}, \tilde{R}, \tilde{U})$ must hold. Observe that $\tilde{Z}^{\dagger } = \tilde{Z}$ cannot be the case since it implies $\tilde{R}^{\dagger } \!=\! \tilde{R}$ and $\tilde{U}^{\dagger } \!=\! \tilde{U}$ to fulfill (32) and (33). Thus, we have $\tilde{Z}^{\dagger } \!\ne \! \tilde{Z}$ and $\tilde{Z}^{\star } \!=\! \tilde{Z}^{\dagger }/\tilde{Z}\ne 1$.

Next, we consider the case of $(M_1,\dots ,M_k) \ne (M^{\dagger }_1,\dots ,M^{\dagger }_k)$. In this case, there exists $i^{\star }$ for which $M_{i^\star } \ne M^{\dagger }_{i^{\star }}$ holds. We claim that randomness $\chi _{i^{\star }}$ is information-theoretically hidden from the view of the adversary. Namely, for any view of the adversary and for any $\chi _{i^{\star }}$, there exists a consistent coin toss which yields the view.

From now, we consider a group element by its index with respect to base $G$ and $\tilde{G}$ and denote the index with the corresponding lower-case letter. For instance, we represent $G_z$ by $g_z :=\log _G G_z$. The independent group elements $(G_z, H_z, H_{u}, G_1, H_1, \dots , G_k, H_k,$ $A, B, Z)$ given to ${{\mathcal {A}}}$ are translated to $(g_z, h_z, h_u, g_1, h_1, \dots , g_k, h_k, a, b, z)$. Note that $R$ and $U$ are uniquely determined from other group elements. Message $(m_1,\dots ,m_k)$ is in the view of ${{\mathcal {A}}}$ as well. Then, for the simulated public key and one-time signature, the following relations hold among the variables in the view and the coins chosen by the reduction algorithm:

$$\begin{aligned}&g_i = g_z \chi _i + \gamma _i, \quad h_i = h_z \chi _i + h_u \delta _i \quad (\text {for} \,\,i=1,\dots ,{k})\end{aligned}$$

(35)

$$\begin{aligned}&a = g_z {\zeta } + {\rho }, \quad b = h_z {\zeta } + h_u {\varphi },\end{aligned}$$

(36)

$$\begin{aligned}&\textstyle z = {\zeta } + \sum \limits _{i=1}^{{k}} - m_i {\chi _i}. \end{aligned}$$

(37)

Let $\chi _{i}$ for all $i \ne i^{\star }$ be fixed to any value. Then, for every assignment to $\chi _{i^{\star }}$, there exist consistent $\gamma _{i^{\star }}$ and $\delta _{i^{\star }}$ that fulfill (35). Also, there exist $\rho$, $\varphi$ and $\zeta$ that satisfy (37) and (36). Accordingly, any choice of $\chi _{i^{\star }}$ is consistent with the adversary’s view. Due to the factor $({M^{\dagger }_{i^{\star }}}/{M_{i^{\star }}})^{\chi _{i^{\star }}}$, with ${M^{\dagger }_{i^{\star }}}/{M_{i^{\star }}} \ne 1$, variable $\tilde{Z}^{\star }$ distributes uniformly over $\tilde{{{\mathbb {G}}}}$ depending on $\chi _{i^\star }$. Thus, $\tilde{Z}^{\star } = 1$ happens only with negligible probability.$\square$

4.2 Construction in Asymmetric Setting

In the case of $\Lambda \in \{\Lambda _{\mathsf{xdh }}, \Lambda _{\mathsf{sxdh }}\}$, we can construct a more efficient scheme, $\mathsf{OTS{2} }$, that halves $\mathsf{OTS{1} }$ just like $\mathsf{HTC{2} }$ does for $\mathsf{HTC{1} }$.

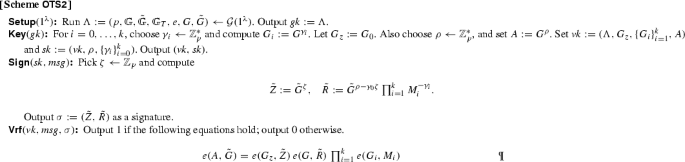
Theorem 8

$\mathsf{OTS{2} }$ is a one-time signature scheme that is strongly unforgeable against one-time chosen-message attacks if DBP holds for ${\mathcal {G}}$.

Theorem 8 can be proven in the same manner as done for Theorem 7 only by dropping non-existing variables.

Remark on Signing Messages from Both Groups. By swapping the roles of ${{\mathbb {G}}}$ and $\tilde{{{\mathbb {G}}}}$, we obtain a dual scheme $\mathsf{OTS{2'} }$ whose messages are in ${{\mathbb {G}}}$. By using these two schemes in a fixed order, we construct a scheme that signs a bilateral message $msg :=(M_1,\dots ,M_{{k}_m}, N_1,\dots ,N_{{k}_n}) \in \tilde{{{\mathbb {G}}}}^{{k}_m} \times {{\mathbb {G}}}^{{k}_n}$: Sign $(M_1,\dots ,M_{{k}_m})$ with $\mathsf{OTS{2} }$ to obtain $\sigma _{m}$ and then sign $(N_1,\dots ,N_{{k}_n})$ with $\mathsf{OTS{2'} }$ to obtain $\sigma _{n}$; define $\sigma :=(\sigma _m,\sigma _n)$ as the signature for $msg$. The signature is accepted if $\sigma _m$ is a valid signature for $\mathsf{OTS{2} }$ and $\sigma _n$ is a valid signature for $\mathsf{OTS{2'} }$. With $\Lambda = \Lambda _{\mathsf{sxdh }}$, the resulting scheme is strongly unforgeable against one-time adaptive chosen-message attacks. More precisely, the security is proven based on DBP and its dual assumption implied by DDH in ${{\mathbb {G}}}$ and $\tilde{{{\mathbb {G}}}}$, respectively.

Remark on Reusing Public Keys. In [2], it is shown that $\mathsf{OTS{2} }$ can be used as partially one-time signature scheme where only element $A$ is updated for every signing and all remaining elements in $vk$ can be reused. We refer to [2] for the formal security notion and a proof.

Though it is not covered by [2], the same is true for $\mathsf{OTS{1} }$ where only $A$ and $B$ must be refreshed before signing. The intuition is that, for the information-theoretical argument in the security proof, elements $A$ and $B$ provide random one-time pads $\rho$ and $\varphi$, respectively, that perfectly hide the sensitive information $\chi _{i^{\star }}$ for signing. Hence by refreshing $A$ and $B$ for every signing, new randomness hides $\chi _{i^{\star }}$ in the view of the signature. Thus, the information-theoretical argument is preserved.

5 Constant-Size Signatures

This section presents a constant-size structure-preserving signature scheme that yields signatures consisting of 7 group elements independently of the message length, which is a priori fixed by the public key. We then argue how to extend the basic scheme to sign messages with unbounded length allowing linear growth of the signature size with an exact estimation of the growth factor.

5.1 Construction

Our construction combines a trapdoor commitment scheme based on SDP and a strong $q$-type assumption, SFP. A technical obstacle is the “exception,” that besides satisfying Equations (2) and (3), a SFP solution must also satisfy $\tilde{Z}^{\star } \ne 1$. The signature scheme should not explicitly handle exceptions because the condition $\tilde{Z}\ne 1$ is not trivial to prove and affects the efficiency when proving a knowledge of a signature. We address this problem by involving another set of elements $(A_0, \tilde{A}_0)$ and $(B_0, \tilde{B}_0)$ in the verification predicate. In the proof of unforgeability, these elements hold a secret random offset $\tilde{g}^{\zeta }$ that will be multiplied to $\tilde{Z}$ in a forged signature so that the answer to SFP, $\tilde{Z}^{\star } = \tilde{Z}\tilde{G}^{\zeta }$, happens to be $1$ only by chance. (The real proof is slightly more involved.) The randomization techniques from Sect. 2.7 also help the construction and the security proof in such a way that the signature elements are uniform conditioned on satisfying the verification equations.

The message space of our signature scheme is $\tilde{{{\mathbb {G}}}}^{{k}}$ for an arbitrary constant ${k}$. Let in the following $msg :=(M_1,\dots ,M_{k}) \in \tilde{{{\mathbb {G}}}}^{{k}}$ be a message to be signed.

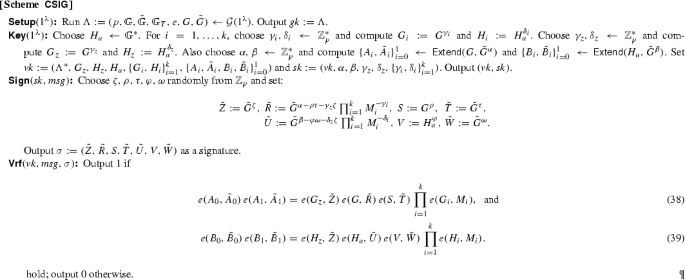
Correctness is verified by inspecting that

$$\begin{aligned} \text{(right-hand } \text{ of } \text{(38)) }&= e(G_z,\tilde{Z})\, e(G,\tilde{R})\, e(S, \tilde{T})\, \textstyle \prod \limits _{i=1}^{{k}} e(G_{i},M_{i}) \\&= e\left( G^{\gamma _z},\tilde{G}^{\zeta }\right) \\&\textstyle e\left( G,\tilde{G}^{\alpha - \rho \tau -\gamma _z\zeta } \prod \limits _{i=1}^{{k}} M_i^{-\gamma _i}\right) e\left( G^{\rho },\tilde{G}^{\tau }\right) \, \prod \limits _{i=1}^{{k}} e\left( G^{\gamma _i},M_{i}\right) \\&= \; e\left( G,\tilde{G}^\alpha \right) \\&= \; \text{(left } \text{ hand } \text{ of } \text{(38)) }. \end{aligned}$$

holds. Relation (39) is verified in the same manner.

Given a signature $(\tilde{Z},\tilde{R},S,\tilde{T},\tilde{U},V,\tilde{W})$, one can randomize every element except for $\tilde{Z}$ by applying the sequential randomization technique. Let $(\tilde{R}',S',\tilde{T}',\tilde{U}',V',\tilde{W}') \leftarrow \mathsf{SigRand }(\tilde{R},S,\tilde{T},\tilde{U},V,\tilde{W})$ be an algorithm defined as follows. If $\tilde{T}= 1$, set $S= 1$ and choose $\tilde{T}\leftarrow \tilde{{{\mathbb {G}}}}^*$. Then, choose $\varrho \leftarrow \mathbb {Z}_p$ and compute $\tilde{R}' = \tilde{R}\,\tilde{T}^{\varrho }$ and $(S',\tilde{T}') \leftarrow \mathsf{Rand }(SG^{-\varrho }, \tilde{T})$; compute $(\tilde{U}', V', \tilde{W}')$ from $(\tilde{U},V,\tilde{W})$ analogously. The resulting $(\tilde{R}',S',\tilde{T}',\tilde{U}',V',\tilde{W}')$ distributes uniformly over $(\tilde{{{\mathbb {G}}}}\times {{\mathbb {G}}}\times \tilde{{{\mathbb {G}}}})^2$ under the constraint that $e(G, \tilde{R})\, e(S,\tilde{T}) = e(G, \tilde{R}')\, e(S',\tilde{T}')$ and $e(H_{u}, \tilde{U})\, e(V,\tilde{W}) = e(H_{u}, \tilde{U}')\, e(V',\tilde{W}')$. Accordingly, $(S',\tilde{T}',V',\tilde{W}')$ is independent of $\tilde{Z}$, the message and the verification key. This is a useful property, since it can reduce the size of proofs of knowledge of signatures: The randomized $(S',\tilde{T}',V',\tilde{W}')$ can be exposed, as they do not reveal anything about the hidden signature.

Theorem 9

$\mathsf{CSIG }$ is EUF-CMA against adversaries making up to $q$ signing queries if $q$-SFPA holds for ${\mathcal {G}}$.

Proof

Let ${\mathcal {A}}$ be an adversary that after adaptively querying the signing oracle on messages $\vec {M}_j$, for $j=1,\dots ,q$, and receiving signatures $\sigma _j$ has non-negligible advantage of forging a signature on a message $\vec {M}^{\dagger }\not \in \{\vec {M}_j\}_{j=1}^q$. We construct a reduction algorithm which takes an input $\Lambda$, $G_z$, $H_z$, $H_{u}$, $(A,\tilde{A}),(B,\tilde{B})$ and uniformly chosen tuples ${I}_j$ for $j=1,\dots ,q$ as defined in Assumption 8, and simulates the view of ${\mathcal {A}}$ in the attack environment as follows:

Simulating $\mathsf{CSIG }.\mathsf{Key }$::

Use $(G_z, H_z, H_{u})$ as given in the input. For $i=1,\dots ,{k}$ set $G_i := G_z^{\chi _i} G^{\gamma _i}$ and $H_i := H_z^{\chi _i} H_{u}^{\delta _i}$, where $\chi _i, \gamma _i$, $\delta _i$ $\leftarrow$ $\mathbb {Z}_p$. As the probability that any $G_i$ or $H_i$, $i=1,\ldots ,{k}$, is equal to $1_{{{\mathbb {G}}}}$ is negligible, the reduction simply aborts in such cases. Otherwise, all group elements are uniformly random in ${{\mathbb {G}}}^*$, like in the key generation algorithm. Then, select $\zeta$, $\rho$, $\varphi \leftarrow \mathbb {Z}_p$, and compute $((A_{0},\tilde{A}_{0}), (A_{1},\tilde{A}_{1})) \leftarrow \mathsf{RandSeq }((G_z^{\zeta } G^{\rho },\tilde{G}), (A, \tilde{A}))$ and $((B_{0},\tilde{B}_{0}), (B_{1},\tilde{B}_{1})) \leftarrow \mathsf{RandSeq }((H_z^{\zeta } H_{u}^{\varphi }, \tilde{G}), (B, \tilde{B}))$.

For convenience, denote $G_z^{\zeta } G^{\rho }$ by $A'$ and $H_z^{\zeta } H_{u}^{\varphi }$ by $B'$.

The verification key is $vk = (G_z, H_z, H_{u}, \{G_i, H_i\}_{i=1}^k, \{A_i, \tilde{A}_i, B_i, \tilde{B}_i\}^{1}_{i=0})$.

Simulating $\mathsf{CSIG }.\mathsf{Sign }$::

Given a message $\vec {M}$, take a fresh tuple ${I}_j= (\tilde{Z}_{j},\tilde{R}_{j},\tilde{U}_{j}, S_{ij},$ $\tilde{T}_{ij},V_{ij},\tilde{W}_{ij}) \in \tilde{{{\mathbb {G}}}}^*\times \tilde{{{\mathbb {G}}}}\times \tilde{{{\mathbb {G}}}}\times {{\mathbb {G}}}\times \tilde{{{\mathbb {G}}}}\times {{\mathbb {G}}}\times \tilde{{{\mathbb {G}}}}$ from the input instance. Then, compute

$$\begin{aligned} \begin{array}{llll} \tilde{Z}:= \tilde{Z}_{j}\, \tilde{G}^{\zeta }\, \prod \limits _{i=1}^{{k}} M_i^{-\chi _i}, \quad &{} \tilde{R}:= \tilde{R}_{j}\, \tilde{G}^{\rho }\, \prod \limits _{i=1}^{{k}} M_i^{-\gamma _i}, \quad S:= S_{j},\quad \tilde{T}:=\tilde{T}_{j}, \\ &{} \tilde{U}:= \tilde{U}_{j}\, \tilde{G}^{\varphi }\, \prod \limits _{i=1}^{{k}} M_i^{-\delta _i}, \quad V:= V_{j},\quad \tilde{W}:=\tilde{W}_{j}. \end{array} \end{aligned}$$

The signature is $\sigma := (\tilde{Z},\tilde{R},S,\tilde{T},\tilde{U},V,\tilde{W})$. It is easy to verify that the signature satisfies the verification equations.

When ${\mathcal {A}}$ outputs $({\vec {M}^{\dagger }}, (\tilde{Z}^{\dagger },\tilde{R}^{\dagger },S^{\dagger },\tilde{T}^{\dagger },\tilde{U}^{\dagger },V^{\dagger },\tilde{W}^{\dagger }))$, compute

$$\begin{aligned} \begin{array}{llll} \tilde{Z}^{\star } := \tilde{Z}^{\dagger }\, {\tilde{G}}^{-\zeta } \prod \limits _{i=1}^{{k}} {(M_i^{\dagger })}^{\chi _i}, \quad \tilde{R}^{\star } := \tilde{R}^{\dagger }\, {\tilde{G}}^{-\rho } \prod \limits _{i=1}^{{k}} {(M_i^{\dagger })}^{\gamma _i}, \quad \tilde{U}^{\star } := \tilde{U}^{\dagger }\, {\tilde{G}}^{-\varphi } \prod \limits _{i=1}^{{k}} {(M_i^{\dagger })}^{\delta _i}, \end{array} \end{aligned}$$

and set $S^{\star } := S^{\dagger }$, $\tilde{T}^{\star } := \tilde{T}^{\dagger }$, $V^{\star } := V^{\dagger }$, and $\tilde{W}^{\star } := \tilde{W}^{\dagger }$. If any of the parameters $\chi _1,\ldots ,\chi _{k}$ is $0$, the reduction algorithm aborts; otherwise, it outputs $(\tilde{Z}^{\star },\tilde{R}^{\star },S^{\star },\tilde{T}^{\star },\tilde{U}^{\star },V^{\star },\tilde{W}^{\star })$. The probability of aborting is negligible because the parameters are chosen uniformly at random. We can therefore ignore those cases in our analysis without affecting the overall outcome. This completes the description of the reduction algorithm.

The above signatures are correctly distributed, and thus, ${\mathcal {A}}$ outputs a successful forgery with a non-negligible probability. Then, for the output of the reduction algorithm, it holds that

$$\begin{aligned}&e(G_z, \tilde{Z}^{\star })\,e(G,\tilde{R}^{\star })\, e(S^{\star },\tilde{T}^{\star })\\&\quad \textstyle =e\left( G_z, \tilde{Z}^{\dagger }\, {\tilde{G}}^{-\zeta } \prod \limits _{i=1}^{{k}} {(M_i^{\dagger })}^{\chi _i}\right) e\left( G, \tilde{R}^{\dagger }\, {\tilde{G}}^{-\rho } \prod \limits _{i=1}^{{k}} {(M_i^{\dagger })}^{\gamma _i}\right) \, e\left( S^{\dagger },\tilde{T}^{\dagger }\right) \\&\quad =e\big (G_z^{-\zeta } G^{-\rho }, \tilde{G}\big )\, e\big (G_z, \tilde{Z}^{\dagger }\big )\, e\big (G, \tilde{R}^{\dagger }\big )e\big (S^{\dagger },\tilde{T}^{\dagger }\big )\, \textstyle \prod \limits _{i=1}^{{k}} e\big (G_i, M^{\dagger }_i\big )\\&\quad =e\big (G_z^{\zeta }G^{\rho }, \tilde{G}\big )^{-1}\, \textstyle \prod \limits _{i=0}^{1}e(A_i, \tilde{A}_i) \ =\ e(A, \tilde{A}). \end{aligned}$$

One can also verify that $e(G_z, \tilde{Z}^{\star })\,e(H_{u},\tilde{U}^{\star })\, e(V^{\star },\tilde{W}^{\star }) = e(B, \tilde{B})$ holds in the same way.

It remains to show that $\tilde{Z}^{\star }$ is not in $\{1, \tilde{Z}_1, \dots , \tilde{Z}_{q}\}$. For that, first notice that the parameters $\zeta$ and $\{\chi _i\}_{i=1}^{{k}}$ are independent from adversary ${\mathcal {A}}$’s view, as proved in Lemma 6 below. Namely, for any view of the adversary and for any choice of $\zeta$ and $\chi _i$, for $i=1,\dots ,{k}$, there exist unique and consistent parameters $\rho$, $\varphi$, $\gamma _i$, $\delta _i$, $i=1,\dots ,{k}$ and $\tilde{Z}_j$, $\tilde{R}_j$, $\tilde{U}_j$, $j=1,\dots ,q$.

We show that the probability that $\tilde{Z}^{\star } \in \{\tilde{Z}_1,\dots ,\tilde{Z}_q\}$ is negligible. For every $\tilde{Z}_j$ and signature $\sigma = (\tilde{Z},\tilde{R},S,\tilde{T},\tilde{U},V,\tilde{W})$ on a message $\vec {M}$ simulated by using $\tilde{Z}_j$, it holds that

$$\begin{aligned} \frac{\tilde{Z}^{\star }}{\tilde{Z}_{j}} \quad =\quad \frac{ \tilde{Z}^{\dagger }\, {\tilde{G}}^{-\zeta } \prod \limits _{i=1}^{{k}} {(M_i^{\dagger })}^{\chi _i} }{\tilde{Z}\, \tilde{G}^{-\zeta }\, \prod \limits _{i=1}^{{k}} M_{i}^{\chi _i} } \quad =\quad \frac{\tilde{Z}^{\dagger }}{\tilde{Z}} \,\textstyle \prod \limits _{i=1}^{{k}} \Big (\frac{M_i^{\dagger }}{M_{i}}\Big )^{\chi _i}. \end{aligned}$$

Since $\vec {M}^{\dagger }\ne \vec {M}$, there exists $i$ such that $M_i^{\dagger } \ne M_{i}$. Since $\chi _i\in \mathbb {Z}_p^*$ is information-theoretically hidden from the adversary’s view, the probability that $\tilde{Z}^{\star }=\tilde{Z}_{j}$ is negligible due to the term $(M_i^{\dagger }/M_{i})^{\chi _i}$ in the above equation. To show that $\tilde{Z}^{\star } = {(\tilde{Z}^{\dagger })}\, {\tilde{G}}^{-\zeta } \prod _{i=1}^{{k}}$ ${(M_i^{\dagger })}^{\chi _i}$ is equal to $1_{\tilde{{{\mathbb {G}}}}}$ only with negligible probability, notice that $\zeta$ is also independent from the adversary’s view and the claim holds due to the uniform choice of $\zeta$. Therefore, when the reduction algorithm does not abort, the probability that $\tilde{Z}^{\star } \not \in \{1, \tilde{Z}_1, \dots , \tilde{Z}_{q}\}$ is overwhelming.$\square$

Lemma 6

The parameters $\zeta$, $\chi _1$, $\chi _2$, $\ldots$, $\chi _{k}$ chosen by the reduction algorithm in Theorem 9 are independent from ${\mathcal {A}}$’s view, that is, independent from the verification key, the signed messages and the signatures.

Proof

Let $vk := (G_z, H_z, H_{u}, \{G_i, H_i\}_{i=1}^k, \{A_i, \tilde{A}_i, B_i, \tilde{B}_i\}^{1}_{i=0})$ be the verification key the adversary sees, $\vec {M}_1$, $\ldots$, $\vec {M}_q$ be the messages on which ${\mathcal {A}}$ queries the signing oracle, and $\sigma _1$, $\ldots$, $\sigma _q$ be the corresponding signatures. Furthermore, assume that $(A,\tilde{A})$ and $(B,\tilde{B})$ given to the reduction algorithm are also fixed, though ${\mathcal {A}}$ does not see them. That yields unique $A'$ and $B'$ such that

$$\begin{aligned} A_T&\;=\; e(A_0,\tilde{A}_0)\,e(A_1,\tilde{A}_1) \;=\; e(A',\tilde{G})\, e(A,\tilde{A}) \\ B_T&\;=\; e(B_0,\tilde{B}_0)\,e(B_1,\tilde{B}_1) \;=\; e(B',\tilde{G})\,e(B,\tilde{B}) \end{aligned}$$

For any choice $\zeta ^{\star }, \chi _i^{\star } \in \mathbb {Z}_p$ of the parameters $\zeta , \chi _i$ , for $i=1,\dots ,{k}$, there exists a unique coin toss $\rho ^{\star }$, $\varphi ^{\star }$, $\gamma _i^{\star }$, $\delta _i^{\star }$ such that $A'=G_z^{\zeta ^{\star }} G^{\rho ^{\star }}$, $B'=H_z^{\zeta ^{\star }}H_{u}^{\varphi ^{\star }}$, $G_i = G_z^{\chi _i^{\star }} G^{\gamma _i^{\star }}$, and $H_i = H_z^{\chi _i^{\star }} H_{u}^{\delta _i^{\star }}$. This shows that the verification key and the parameters are independent. Next, we show that the chosen parameters remain independent from ${\mathcal {A}}$’s view even after signing $q$ adaptively chosen messages due to the uniform choice of the tuples ${I}_j=(\tilde{Z}_{j},\tilde{R}_{j},S_{j},\tilde{T}_{j},\tilde{U}_{j},V_{j},\tilde{W}_{j})$, $j=1,\ldots ,q$, as defined in Assumption 8.

Let the $j$-th message be $\vec {M}$ and the corresponding signature be $\sigma =$ $(\tilde{Z},\tilde{R},S,\tilde{T},\tilde{U},V,\tilde{W})$. From the specification of the reduction algorithm we have $(S,\tilde{T})$ $=(S_j,\tilde{T}_j)$ and $(V,\tilde{W})=(V_j,\tilde{W}_j)$, where ${I}_j=(\tilde{Z}_{j},\tilde{R}_{j},S_{j},\tilde{T}_{j},\tilde{U}_{j},V_{j},\tilde{W}_{j})$ is the $j$-th tuple given as input. And for the fixed view, $\zeta , \{\chi _i\}_{i=1}^{k}$ determine uniquely the values of $\tilde{Z}_j = \tilde{Z}\, \tilde{G}^{-\zeta }\, \prod _{i=1}^{{k}} M_i^{\chi _i}\,$, $\tilde{R}_j = \tilde{R}\, \tilde{G}^{-\rho }\, \prod _{i=1}^{{k}} M_i^{\gamma _i}\,$, and $\tilde{U}_j = \tilde{U}\, \tilde{G}^{-\varphi }\, \prod _{i=1}^{{k}} M_i^{\delta _i}$. Regardless of the particular choice of parameters $\zeta ^{\star }, \{\chi _i^{\star }\}_{i=1}^{k}$, since $\sigma$ satisfies the signature-verification equations:

$$\begin{aligned} A_T&= e(G_z,\tilde{Z})\, e(G,\tilde{R})\, e(S, \tilde{T})\, \textstyle \prod \limits _{i=1}^{{k}} e(G_{i},M_{i}) \quad \text {and}\\ B_T&= e(H_z,\tilde{Z})\, e(H_{u},\tilde{U})\, e(V, \tilde{W})\, \textstyle \prod \limits _{i=1}^{{k}} e(H_{i},M_{i}), \end{aligned}$$

it is true that the corresponding tuple ${I}^{\star }_j=(\tilde{Z}^{\star }_{j},\tilde{R}^{\star }_{j},S_j,\tilde{T}_j,\tilde{U}^{\star }_{j},V_j,\tilde{W}_j)$ satisfies:

$$\begin{aligned} e(A, \tilde{A})&= e(G_z,\tilde{Z}^{\star }_{j})\, e(G,\tilde{R}^{\star }_{j})\, e(S_j, \tilde{T}_j) \quad \text {and}\nonumber \\ e(B, \tilde{B})&= e(H_z,\tilde{Z}^{\star }_{j})\, e(H_{u},\tilde{U}^{\star }_{j})\, e(V_j, \tilde{W}_j). \end{aligned}$$

(40)

It remains to show that the uniform choice of $\zeta ^{\star }, \{\chi ^{\star }_i\}_{i=1}^{k}$ together with ${\mathcal {A}}$’s view yields uniform distribution for the tuples $I^{\star }_j$, for $j=1,\ldots ,q$, as specified by the assumption description. If that is indeed the case, each set of tuples which could have been given as input to the reduction algorithm is chosen with the same probability. And because for any choice of $\zeta ^{\star },\chi ^{\star }_1,\ldots ,\chi _{k}$, there exists unique set $\{I^{\star }_j\}_{j=1}^q$, those imply that each parameter selection looks equally likely for ${\mathcal {A}}$.

To see the uniformity of $I^{\star }_j$, note again that $(S_j,\tilde{T}_j)$ and $(V_j,\tilde{W}_j)$ are determined uniquely from the view regardless of the choice of parameters. We define the following homomorphism $\phi$:

$$\begin{aligned} \phi _{\tilde{G},\vec {M}}(\zeta ^{\star },\chi ^{\star }_1,\ldots ,\chi ^{\star }_{k}) =\tilde{G}^{-\zeta ^{\star }}\textstyle \prod \limits _{i=1}^{k}M_i^{\chi ^{\star }_i}. \end{aligned}$$

It is easy to verify that for uniformly chosen parameters, the range of $\phi$ is uniformly distributed over $\tilde{{{\mathbb {G}}}}$. This in turn implies that for a fixed $\tilde{Z}$ and uniformly chosen parameters, $\tilde{Z}^{\star }_j=\tilde{Z}$, $\phi (\zeta ^{\star },\chi _1,\ldots ,\chi _{k})$ is uniformly distributed over $\tilde{{{\mathbb {G}}}}$. And because $I^{\star }_j$ satisfies (40), the values of $\tilde{R}^{\star }_j$ and $\tilde{U}^{\star }_j$ are determined uniquely by the other tuple values, which for a fixed view means determined by $\tilde{Z}^{\star }_j$. To sum it up, for a fixed view, the uniform random choice of the parameters gives uniformly distributed $\tilde{Z}^{\star }_j$ which implies the uniformity of $I^{\star }_j$.$\square$

5.2 Extension

Our scheme CSIG in Sect. 5.1 is not automorphic since the size of a message vector is a priori bounded by the verification key and the verification key itself exceeds the bound. There is a standard method to sign unbounded-size messages by using signature schemes with limited message space. The following scheme, denoted by $\mathsf{USIG{} }$, is a minor variation of the one in [65]. Suppose that CSIG is set up to sign messages of size at most $k \ge 3$. To sign message $\vec {M} = (M_1,\dots ,M_n)$ for $n > k$, first encode the size of the message into a group element $M_0 := \langle |\vec {M}|\rangle$. Then, select a random group element $t$ and compute

$$\begin{aligned} \sigma _0&:= \mathsf{CSIG }.\mathsf{Sign } ( sk , t\,||\,\langle 1\rangle \,||\,M_0,...,M_{k-3}),\nonumber \\ \sigma _1&:= \mathsf{CSIG }.\mathsf{Sign } ( sk , t\,||\,\langle 2\rangle \,||\,M_{k-2},...,M_{2k-5}),\ \ldots \end{aligned}$$

(41)

The resulting signature is $\sigma = (t,\sigma _0,\sigma _1,\dots )$, which consists of $\lceil \frac{n+1}{k-2}\rceil \cdot 7 + 1$ group elements.

The scheme $\mathsf{USIG{} }$ is automorphic in the symmetric setting but falls short in the asymmetric setting $\Lambda = \Lambda _{\mathsf{sxdh }}$ where a message vector may consist of elements from ${{\mathbb {G}}}$ and $\tilde{{{\mathbb {G}}}}$. We construct a scheme, $\mathsf{XUSIG }$, that signs messages consisting of elements in ${{\mathbb {G}}}$ and $\tilde{{{\mathbb {G}}}}$ for $\Lambda =\Lambda _{\mathsf{sxdh }}$ as follows. Let $\mathsf{USIG{1} }$ and $\mathsf{USIG{2} }$ be schemes for unbounded-size messages in ${{\mathbb {G}}}$ and $\tilde{{{\mathbb {G}}}}$, respectively. To sign $\vec {M} = (M_1,\dots ,M_n, \tilde{M}_1,\dots ,\tilde{M}_{\tilde{n}}) \in {{\mathbb {G}}}^n \times \tilde{{{\mathbb {G}}}}^{\tilde{n}}$, first pick random tags $T \in {{\mathbb {G}}}$ and $\tilde{T} \in \tilde{{{\mathbb {G}}}}$ such that $e(T,\tilde{G}) = e(G,\tilde{T})$ holds. Then, sign $(T, M_1,\dots ,M_n)$ and $(\tilde{T}, \tilde{M}_1,\dots ,\tilde{M}_{\tilde{n}})$ by using $\mathsf{USIG{1} }$ and $\mathsf{USIG{2} }$. The resulting signature is a concatenation of two signatures from $\mathsf{USIG{1} }$ and $\mathsf{USIG{2} }$. The verification function first checks if $e(T,\tilde{G}) = e(G,\tilde{T})$ holds and then follows the verification for $\mathsf{USIG{1} }$ and $\mathsf{USIG{2} }$.

It is not hard to see that, if the underlying schemes are existentially unforgeable against chosen-message attacks, so are $\mathsf{USIG{} }$ and $\mathsf{XUSIG }$. Thus, schemes $\mathsf{USIG{} }$ and $\mathsf{XUSIG }$ are secure automorphic signature schemes in symmetric and asymmetric bilinear-group setting, respectively.

6 Automorphic Signatures

In this section, we present an efficient construction of an automorphic signature scheme, which was also the first efficient structure-preserving signature scheme in the literature. In this scheme public keys are Diffie–Hellman pairs, that is, $(G^x,\tilde{G}^x)$, for some $x\in {{\mathbb {Z}}}_p$. Messages are also of this form: $(G^m,\tilde{G}^m)$. We then present a generic method to extend the message space so we can sign several messages of that form at once.

6.1 Construction

Boneh and Boyen [22] show that their SDH assumption implies a signature scheme which is existentially unforgeable against adversaries that only get signatures on random messages (the scheme corresponds to Problem 1 stated before Assumption 9; page 15). Analogously, ADH-SDH immediately yields an (automorphic) scheme secure against “random-message attacks” if we consider $(X,\tilde{Y})$ as the public key, $(V,\tilde{W})$ as a message in $\mathcal {DH}=\{(G^v,\tilde{G}^v)\,|\,v\in {{\mathbb {Z}}}_p\}$ and $(A,B,\tilde{D})$ as the signature. We show how to transform this into a strongly EUF-CMA-secure signature scheme by assuming AWF-CDH. We add some more randomness to the signature that in our reduction lets us map a query for a message chosen by the adversary to a given tuple $(A_i,B_i,\tilde{D}_i,V_i,\tilde{W}_i)$ from an ADH-SDH instance. AWF-CDH then asserts that the adversary cannot produce a new signature/message pair $\big ((A^*,B^*,\tilde{D}^*,R^*,\tilde{S}^*),(M^*,\tilde{N}^*)\big )$ that maps back to a tuple from the instance (see the proof of Theorem 10). We get the following efficient automorphic signature construction, whose signatures are in ${{\mathbb {G}}}^3\times \tilde{{{\mathbb {G}}}}^2$. The scheme can also be defined over symmetric bilinear groups, in which case we replace $\tilde{G}$ by a random generator $H$ of ${{\mathbb {G}}}$.

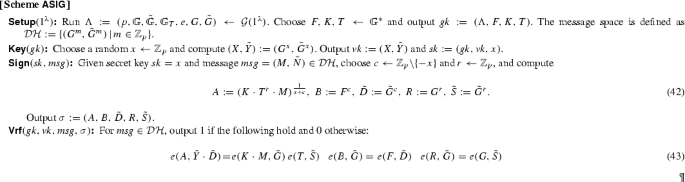
Theorem 10

Signature scheme $\mathsf{ASIG{} }$ is ${\hbox {sEUF-CMA}}$ against adversaries making at most $q-1$ adaptive chosen-message queries if $q$-ADH-SDH and AWF-CDH hold for ${\mathcal {G}}$.

Proof

Consider an adversary that after receiving parameters $(\Lambda ,F,K,T)$ and public key $(X,\tilde{Y})$ is allowed to ask for $q-1$ signatures $(A_i,B_i,\tilde{D}_i,R_i,\tilde{S}_i)$ on messages $(M_i,\tilde{N}_i)\in \mathcal {DH}$ of its choice and outputs $(M,\tilde{N})\in \mathcal {DH}$ and a valid signature $(A,B,\tilde{D},R,\tilde{S})$ on it, such that either $(M,\tilde{N})$ was never queried, or $(M,\tilde{N})=(M_i,\tilde{N}_i)$ and $(A,B,\tilde{D},R,\tilde{S})\ne (A_i,B_i,\tilde{D}_i,R_i,\tilde{S}_i)$.

We distinguish two kinds of forgers: An adversary is called of Type A if its output satisfies

$$\begin{aligned} e(T,\tilde{S}\cdot \tilde{S}_i^{-1})\ne e(M_i\cdot M^{-1},\tilde{G})\,\quad \vee \quad \,B\ne B_i \end{aligned}$$

(44)

for all $i \in \{1,\dots ,q-1\}$. Otherwise, it is called of Type B. We will use the first type to break $q$-ADH-SDH and the second type to break AWF-CDH.

Adversary Type A. Let $\big (\Lambda ,F,K,X,\tilde{Y},(A_i,B_i,\tilde{D}_i,V_i,\tilde{W}_i)_{i=1}^{q-1}\big )$ be a $q$-ADH-SDH challenge. By (7), it satisfies

$$\begin{aligned} e(A_i,\tilde{Y}\cdot \tilde{D}_i)&= e(K\cdot V_i,\tilde{G}),&e(B_i,\tilde{G})&=e(F,\tilde{D}_i),&e(V_i,\tilde{G})&=e(G,\tilde{W}_i) \end{aligned}$$

(45)

for all $i \in \{1,\dots ,q-1\}$. Let ${\mathcal {A}}$ be a forger of Type A. Choose $t\leftarrow {{\mathbb {Z}}}_p$ and give parameters $(\Lambda ,F,K,T\!:=\!G^t)$ and the public key $(X,\tilde{Y})$ to ${\mathcal {A}}$. The $i$-th query for $(M_i,\tilde{N}_i)\in \mathcal {DH}$ is answered as

$$\begin{aligned} \textstyle \big (A_i,B_i,\tilde{D}_i,R_i:=(V_i\cdot M_i^{-1})^\frac{1}{t}, \tilde{S}_i=(\tilde{W}_i\cdot \tilde{N}_i^{-1})^\frac{1}{t}\big ) .\end{aligned}$$

(46)

This satisfies the verification equations (43): $e(B_i,\tilde{G})\mathop {=}\limits ^{(45)} (F,\tilde{D}_i)$,

$$\begin{aligned} e(R_i,\tilde{G})&= e((V_i\cdot M_i^{-1})^\frac{1}{t},\tilde{G}) = e(V_i,\tilde{G})^\frac{1}{t}\,e(M_i,\tilde{G})^{-\frac{1}{t}}\nonumber \\&= e(G,\tilde{W}_i)^\frac{1}{t}\,e(G,\tilde{N}_i)^{-\frac{1}{t}} = e(G,\tilde{S}_i) ,\end{aligned}$$

(47)

where the third equation follows from $(V_i,\tilde{W}_i),(M_i,\tilde{N}_i)\in \mathcal {DH}$. Finally

$$\begin{aligned} e(A_i,\tilde{Y}\cdot \tilde{D}_i) \mathop {=}\limits ^{(45)} e(K\cdot V_i,\tilde{G}) \mathop {=}\limits ^{(46)} e(K\cdot (R_i^t\cdot M_i),\tilde{G}) = e(K\cdot M_i,\tilde{G})\,e(R_i\cdot \tilde{G})^t\\ \mathop {=}\limits ^{(47)} e(K\cdot M_i,\tilde{G})\,e(G\cdot \tilde{S}_i)^t = e(K\cdot M_i,\tilde{G})\,e(T\cdot \tilde{S}_i) .\end{aligned}$$

Moreover, the oracle answer in (46) it is correctly distributed since $v_i$ is uniformly random in the ADH-SDH instance. The signing oracle is thus perfectly simulated.

If the adversary produces a valid signature/message pair $((A,B,\tilde{D},R,\tilde{S}),(M,\tilde{N}))$ then by the last 2 equations of (43), there exist $c,r$ such that $B=F^c,\tilde{D}=\tilde{G}^c,R=G^r,\tilde{S}=\tilde{G}^r$, and

$$\begin{aligned} e(A,\tilde{Y}\cdot \tilde{D})=e(K\cdot M,\tilde{G})\,e(T,\tilde{S}).\end{aligned}$$

(48)

The tuple $(A,B,\tilde{D},V:=R^t\cdot M,\tilde{W}:=\tilde{S}^t\cdot \tilde{N})$ satisfies the equations of ADH-SDH tuples in (7), since $(B,\tilde{D})$ and $(V,\tilde{W})$ are Diffie–Hellman pairs and

$$\begin{aligned} e(K\cdot V,\tilde{G})=e(K\cdot (G^r)^t\cdot M,\tilde{G})=e(K\cdot M,\tilde{G})\,e(T,\tilde{S})\mathop {=}\limits ^{(48)} e(A,\tilde{Y}\cdot \tilde{D}) .\end{aligned}$$

Moreover, it is a solution for the ADH-SDH instance, since it is a new tuple: assume that for some $i$ we have $B=B_i$ and $\tilde{W}=\tilde{W}_i$, that is $\tilde{S}^t\cdot \tilde{N}=\tilde{S}_i^t\cdot \tilde{N}_i$. Since $(M,\tilde{N}),(M_i,\tilde{N}_i)\in \mathcal {DH}$, we have $e(T,\tilde{S})\,e(M,\tilde{G})=e(G^t,\tilde{S})\,e(G,\tilde{N})=e(G,\tilde{S}^t\cdot \tilde{N})= e(G,\tilde{S}_i^t\cdot \tilde{N}_i)=e(T,\tilde{S}_i)\,e(G,\tilde{N}_i)=e(T,\tilde{S}_i)\,e(M_i,\tilde{G})$. We have thus $e(T,\tilde{S}\cdot \tilde{S}_i^{-1})=e(M_i\cdot M^{-1},\tilde{G})$ and $B=B_i$ which contradicts (44) and thus the fact that ${\mathcal {A}}$ is of Type A.

Adversary Type B. Let $(\Lambda ,T=G^t)$ be an AWF-CDH instance (note that $T$ corresponds to $A$ in Assumption 3). Let ${\mathcal {A}}$ be a forger of Type B. Pick $F,K\leftarrow {{\mathbb {G}}}$ and $x\leftarrow {{\mathbb {Z}}}_p$, set $X:=G^x$, $\tilde{Y}:=\tilde{G}^x$ and give the adversary parameters $(\Lambda ,F,K,T)$ and public key $(X,\tilde{Y})$. Answer a signing query on $(M_i,\tilde{N}_i)\in \mathcal {DH}$ by returning a signature $(A_i,B_i,\tilde{D}_i,R_i,\tilde{S}_i)$ produced by $\mathsf{ASIG{} }.\mathsf{Sign }$ with $x$ as a secret key. Suppose ${\mathcal {A}}$ returns $((A,B,\tilde{D},R,\tilde{S}),(M,\tilde{N}))$ satisfying (43) such that for some $i$:

$$\begin{aligned} e(T,\tilde{S}\cdot \tilde{S}_i^{-1})&= e(M_i\cdot M^{-1},\tilde{G}) \qquad B=B_i \end{aligned}$$

(49)

Then, $(M^*:=M_i\cdot M^{-1},\tilde{N}^*:=\tilde{N}_i\cdot \tilde{N}^{-1},R^*:=R\cdot R_i^{-1},\tilde{S}^*:=\tilde{S}\cdot \tilde{S}_i^{-1})$ is an AWF-CDH solution:

It satisfies the equations in (1): $e(T,\tilde{S}^*)=e(T,\tilde{S}\cdot \tilde{S}^{-1}) \mathop {=}\limits ^{(49)} e(M_i\cdot M_i^{-1},\tilde{G}) = e(M^*,\tilde{G})$, and the two remaining equations in (1) follow since $(M_i,\tilde{N}_i)$, $(R_i,\tilde{S}_i)$, $(M,\tilde{N})$ and $(R,\tilde{S})$ are all Diffie–Hellman pairs and therefore $(M^*,\tilde{N}^*)$ and $(R^*,\tilde{S}^*)$ are in $\mathcal {DH}$ well. Moreover, $(M^*,\tilde{N}^*,R^*,\tilde{S}^*)$ is non-trivial: If $M^*=1=R^*$, then $M=M_i$ and $R=R_i$; since, moreover, $B=B_i$ and since the values $M,B$ and $R$ completely determine a message/signature pair, this means that ${\mathcal {A}}$ returned a message/signature pair from one of its queries, meaning ${\mathcal {A}}$ did not break strong unforgeability.$\square$

6.2 Extension

In this section, we show how to extend the message space of automorphic signature schemes. The messages of the scheme from the previous section consist of one pair of group elements. Known generic methods for extending the message space require extra elements in the message allowing to glue message blocks together as shown in Sect. 5.2; they thus do not work here. Our approach is to generate a fresh ephemeral key for each message block and authenticate these keys by using the persistent key. As this does not guarantee the order of the message blocks, we bind the message-block number to the corresponding ephemeral key using the group operation.

Let $\mathsf{ASIG }$ be an automorphic signature scheme whose verification key consists of an element of a group ${{\mathbb {H}}}$ of order $p$. For the scheme in Sect. 6.1, this group ${{\mathbb {H}}}$ is $\mathcal {DH}:=\{(G^x,\tilde{G}^x)\,|\,x\in {{\mathbb {Z}}}_p\}$, a subgroup of the direct product of source groups ${{\mathbb {G}}}\times \tilde{{{\mathbb {G}}}}$. Let $\langle n\rangle$ denote an efficiently computable injective mapping from $n \in \{1,\dots ,n_{max}\}$ to ${{\mathbb {H}}}^*$ where $n_{max}$ is larger than any polynomial in $\lambda$. We require that, for any $n$ and $n'$ in $\{1,\dots ,n_{max}\}$, it holds that $\langle n\rangle \cdot \langle n'\rangle \ne 1\in {{\mathbb {H}}}$. (A simple example for $n_{max}\ll p$ would be $\langle n\rangle :=H^n$, where $H$ generates ${{\mathbb {H}}}$.) To simplify notation when dealing with several keys that also act as messages, we write them as subscript when they act as keys; for instance, we write $\mathsf{ASIG }.\mathsf{Sign } _{{ sk}}({ vk}_0)$ for signing message ${ vk}_0$ with key ${ sk}$.

In the following, we construct $\mathsf{ASIG{2} }$ that signs messages $msg = \{M_1,\dots ,M_n\}\in {{\mathbb {H}}}^n$ for an arbitrary $n$ that does not depend on the verification-key length. It outputs a signature of size $(3n + 2)\cdot |{\sigma }_{\mathsf{asig } }| + (n + 1)\cdot |{{ vk}}_{\mathsf{asig } }|$ where $|{\sigma }_{\mathsf{asig } }|$ and $|{{ vk}}_{\mathsf{asig } }|$ denote the size of a signature and a verification key of the underlying scheme $\mathsf{ASIG }$, respectively.

Theorem 11

If $\mathsf{ASIG }$ is EUF-CMA, then so is $\mathsf{ASIG{2} }$.

Proof

We follow the game transformation style for proving the theorem. Starting from the chosen-message attack against $\mathsf{ASIG{2} }$, we change the game slightly and eventually see that the adversary can never win the game.

Game 0.:

(Standard EUF-CMA game.) An adversary is given verification key ${ vk}$ and whenever it makes signing query for $msg$, signing oracle ${\mathcal {O}}_{\mathsf{sign }}$ returns $\sigma \leftarrow \mathsf{ASIG{2} }.\mathsf{Sign }({ sk}, msg )$. The adversary eventually outputs a forgery, ${\sigma }^{\dagger } = ({ vk}^{\dagger }_i,\delta ^{\dagger }_i,\xi ^{\dagger }_i,\gamma ^{\dagger }_i)_{i=0}^{n^{\dagger }}$ and $msg ^{\dagger } = (M^{\dagger }_1,\dots ,M^{\dagger }_{n^{\dagger }})$.

Let us define some notations. Let $\Pr [i]$ denote the probability that the adversary outputs a valid forgery in Game $i$. In particular, $\Pr [0] = \epsilon$ is the probability of breaking $\mathsf{ASIG{2} }$.

Let $Q_{m,\sigma }= \{( msg ,{\sigma })\}$ be the transcript exchanged between the adversary and ${\mathcal {O}}_{\mathsf{sign }}$. Let $q_s$ and $n_{max}$ denote the number of signing queries and the maximum message length, which are bounded by polynomials in $\lambda$. For a public key $\textit{vk}$ with corresponding $\textit{sk}$, let ${\mathcal {I}}_{\textit{vk}}$ denote messages given as input to $\mathsf{ASIG }.\mathsf{Sign } _{\textit{sk}}(\,\cdot \,)$ while ${\mathcal {O}}_{\mathsf{sign }}$ is computing signatures. If $\textit{vk}$ is not used by ${\mathcal {O}}_{\mathsf{sign }}$, then ${\mathcal {I}}_{\textit{vk}} = \emptyset$.

Let $\epsilon _{{ vk}}$ be the highest probability that a key is generated by $\mathsf{ASIG }.\mathsf{Key }$. We assume that $\epsilon _{{ vk}}$ is negligible in the security parameter, which is the case for the scheme in Sect. 6.1, where $\epsilon _{{ vk}}= 1/p$.

Game 1.:

Abort the game if there is a public key ${ vk}_i$ that appears more than once in $Q_{m,\sigma }$.

As each signature in $Q_{m,\sigma }$ includes at most $n_{max}+1$ randomly chosen public keys, the probability of aborting is bounded by $\big (q_s(n_{max}+1)\big )^2\cdot \epsilon _{{ vk}}$. We thus have $|\Pr [0]-\Pr [1]| \le \big (q_s(n_{max}+1)\big )^2\cdot \epsilon _{{ vk}}$, which is negligible in the security parameter.

Game 2.:

Abort the game if there is a signature $({ vk}_i,\delta _i,\xi _i,\gamma _i)_{i=0}^{n}$ in $Q_{m,\sigma }$ such that ${ vk}_i = { vk}_j \cdot \langle j\rangle$ holds for some $0<i,j\le n$.

Observe that ${ vk}_i = { vk}_i \cdot \langle i\rangle$ does not happen since $\langle i\rangle \ne 1$. For every fixed $i$, the probability that there exists $j$ for ${ vk}_i = { vk}_j \cdot \langle j\rangle$ is bounded by $(n_{max}-1)\cdot \epsilon _{{ vk}}$. As there are at most $q_s$ signatures, the probability of aborting is upper bounded by $q_s(n_{max}-1)\cdot \epsilon _{{ vk}}$. We thus have $|\Pr [1]-\Pr [2]| < q_s(n_{max}-1)\cdot \epsilon _{{ vk}}\,$, which is negligible.

Game 3.:

Abort the game if there is a signature $({ vk}_i,\delta _i,\xi _i,\gamma _i)_{i=0}^{n}$ in $Q_{m,\sigma }$ such that ${ vk}_i = \langle n\rangle$ holds for some $0<i\le n$.

For each signature, this happens with probability $n \,\epsilon _{{ vk}}$ due to the randomness of ${ vk}_j$. Accumulating to $q_s$ signatures with maximal length of messages, the probability of aborting for this case is upper bounded by $q_s\cdot n_{max}\cdot \epsilon _{{ vk}}\,$. Thus, $|\Pr [2]-\Pr [3]| < q_s\cdot n_{max}\cdot \epsilon _{{ vk}}\,$, which is negligible.

Game 4.:

Abort the game if there is a signature $({ vk}_i,\delta _i,\xi _i,\gamma _i)_{i=0}^{n}$ in $Q_{m,\sigma }$ such that $\langle n'\rangle \in {\mathcal {I}}_{{ vk}_0}$ holds for some $n'< n$.

The case that $\langle n'\rangle \in \{{ vk}_1,\dots ,{ vk}_n,{ vk}_1\cdot \langle 1\rangle ,\dots ,{ vk}_n\cdot \langle n\rangle \}$ happens with probability at most $2n_{max}\cdot \epsilon _{{ vk}}$ for each signature. Thus, $|\Pr [3]-\Pr [4]| < 2 q_s\cdot n_{max}\cdot \epsilon _{{ vk}}\,$, which is negligible.

Game 5.:

Abort if the output of the adversary satisfies ${ vk}^{\dagger }_0 \not \in {\mathcal {I}}_{{ vk}}$.

This case breaks EUF-CMA of $\mathsf{ASIG }$ since ${ vk}^{\dagger }_0$ is a fresh message correctly signed with respect to ${ vk}$. We thus have $|\Pr [4]-\Pr [5]| < \epsilon _{euf}$, which is negligible as we assume $\mathsf{ASIG }$ is unforgeable.

Now if Game 5 is completed, there exists $msg ^{\star } = (M^{\star }_1,\dots ,M^{\star }_{n^{\star }})$ and unique ${\sigma }^{\star } = ({ vk}^{\star }_i,\delta ^{\star }_i,\xi ^{\star }_i,\gamma ^{\star }_i)_{i=0}^{n^{\star }}$ in $Q_{m,\sigma }$ such that ${ vk}^{\star }_0 = { vk}^{\dagger }_0$.

Game 6.:

Abort if $\{{ vk}^{\dagger }_1,\dots ,{ vk}^{\dagger }_{n^{\dagger }}\} \not \subseteq \{{ vk}^{\star }_1,\dots ,{ vk}^{\star }_{n^{\star }}\}$.

Suppose that there exists ${ vk}^{\dagger }_i$ with ${ vk}^{\dagger }_i \not \in \{{ vk}^{\star }_1,\dots ,{ vk}^{\star }_{n^{\star }}\}$. Observe that ${ vk}^{\dagger }_i \not \in \{\langle n^{\star }\rangle ,{ vk}^{\star }_1 \cdot \langle 1\rangle , \dots , { vk}^{\star }_{n^{\star }} \cdot \langle n^{\star }\rangle \}$ holds since the game did not meet the abort conditions in Game 2 and 3. Then, ${ vk}^{\dagger }_i$ is a new message signed with ${ vk}^{\star }_0$ $(={ vk}^{\dagger }_0)$ since ${ vk}^{\star }_0$ is used only for messages $\{{ vk}^{\star }_1,\dots ,{ vk}^{\star }_{n^{\star }}\} \cup \{\langle n^{\star }\rangle ,{ vk}^{\star }_1 \cdot \langle 1\rangle , \dots , { vk}^{\star }_{n^{\star }} \cdot \langle n^{\star }\rangle \}$. Accordingly, the abort condition in Game 5 is met only if $\mathsf{ASIG{2} }$ is broken with respect to key ${ vk}^{\star }_0$. Taking the probability loss for guessing the target key, the probability of abort in this case is upper bounded by $q_s\epsilon _{euf}$. We thus have $|\Pr [5]-\Pr [6]| < q_s\epsilon _{euf}$ which is negligible.

At this point, we observe that for all $0<i\le n^{\dagger }:{ vk}^{\dagger }_i = { vk}^{\star }_i$. Suppose, on the contrary, that ${ vk}^{\dagger }_i = { vk}^{\star }_j$ happens for some $0<i \le n^{\dagger }$, $i \ne j$, and $0<j \le n^{\star }$. We then have ${ vk}^{\star }_{j} \cdot \langle i\rangle \in {\mathcal {I}}_{{ vk}^{\star }_0}$, which would have caused an abort in Game 2. Furthermore, it holds that $n^{\dagger } = n^{\star }$; otherwise, the game would have aborted as in Game 4. Accordingly, we have $({ vk}^{\dagger }_1,\dots ,{ vk}^{\dagger }_{n^{\dagger }}) = ({ vk}^{\star }_1,\dots ,{ vk}^{\star }_{n^{\star }})$.

Game 7.:

Abort if $\exists i$ s.t. $M^{\dagger }_i \ne M^{\star }_i$.

Since ${ vk}^{\star }_{i}$ is used only for signing $M^{\star }_i$, this case breaks EUF-CMA of $\mathsf{ASIG }$ w.r.t. key ${ vk}^{\star }_{i}$. Taking the probability loss of guessing the target key into account, we have $|\Pr [6]-\Pr [7]| < q_sn_{max}\epsilon _{euf}$.

In Game 7, $msg ^{\dagger } = msg ^{\star }$ holds and the output cannot be a valid forgery. Accumulating the above bounds, we have the probability of successful forgery is negligible if $\mathsf{ASIG }$ is EUF-CMA.$\square$

7 Applications

This section presents two applications that highlight the benefits of structure-preserving signatures. The first one, group signatures with concurrent join, features generic use of structure-preserving signature schemes combined with non-interactive proofs. The second one, round-optimal blind signatures, uses the automorphic signature scheme from Sect. 6 in a specific manner to gain efficiency.

7.1 Group Signatures with Concurrent Join

A group signature, GSIG, consists of 6 algorithms $\mathsf{Setup }, \mathsf{Join }, \mathsf{Sign }, \mathsf{Vrf }$, $\mathsf{Open }$ and $\mathsf{Judge }$ such that:

• $\mathsf{Setup }$ is an algorithm run in a trusted manner. It takes a security parameter and generates a group verification key ${{ vk}}_{\mathrm{g}}$, a certification key ${ sk}_{\mathrm{c}}$ and an opening key ${ sk}_{\mathrm{o}}$. The group verification key is published, the certification key is privately given to an authority called the issuer, whereas the opening key is given privately to another authority called the opener.

• $\mathsf{Join }$ is a pair of interactive algorithms run by the issuer and a user who requests membership of the group. When the protocol is completed, the member obtains a secret user key, $usk$, and the issuer obtains a public user key, $upk$, that consists of some parts of the interaction. The public user key and the identity of the member is stored to the registration record, $reg$.

• $\mathsf{Sign }$ is a signing algorithm run by a group member. On input a secret user key $usk$ and a message $msg$, it outputs a group signature $\pi$ of the message.

• $\mathsf{Vrf }$ is a verification algorithm that on input the group verification key ${{ vk}}_{\mathrm{g}}$, a message $msg$, and a signature $\pi$, outputs $1$ or $0$ meaning acceptance or rejection, respectively.

• $\mathsf{Open }$ is an opening algorithm run by the opener. It takes the opening key ${ sk}_{\mathrm{o}}$, a signature $\pi$ and $reg$ as input and outputs opening information $open$ and identity $id$ of a group member in $reg$.

• $\mathsf{Judge }$ is an algorithm that takes a group signature and an output of $\mathsf{Open }$ as input and outputs $1$ or $0$ that indicate acceptance and rejection, respectively.

Correctness requires that $\mathsf{Vrf }$ outputs 1 for all legitimately generated keys and signatures for any message, and $\mathsf{Judge }$ outputs 1 for all outputs of $\mathsf{Open }$ with legitimate input if $id \ne 0$ and outputs 0 for $id = 0$.

There are several variations and extensions of group signature schemes and their security notions. We focus on anonymity, traceability and non-frameability as essential security notions and follow the definitions in [55].

• Anonymity is defined by a game where an adversary is given a group signature created by one of two honest and correctly registered members and must distinguish which member created the signature. The issuing key and all secret user keys can be exposed to the adversary.

Definition 6

(Anonymity) A group signature scheme is anonymous if for any probabilistic polynomial-time adversary ${{\mathcal {A}}}$

$$\begin{aligned} \Pr \left[ \begin{array}{l} ({{ vk}}_{\mathrm{g}},{ sk}_{\mathrm{c}},{ sk}_{\mathrm{o}}) \leftarrow \mathsf{Setup }(1^\lambda ); \\ b \leftarrow \{0,1\}\\ \tilde{b} \leftarrow {{\mathcal {A}}}^{{{\mathcal {O}}}(b)}({{ vk}}_{\mathrm{g}}, { sk}_{\mathrm{c}}) \end{array}: \begin{array}{l} b = \tilde{b} \end{array} \right] - \frac{1}{2} \end{aligned}$$

is negligible where oracle ${{\mathcal {O}}}$ works as follows.

• On receiving a request, it executes the protocol $\mathsf{Join }$ as the issuer and an honest user. The view of the honest user is returned to ${\mathcal {A}}$.

• Given $upk$ for a new corrupt user, it stores it to $reg$.

• Given a message and two distinct identities, $id_0$ and $id_1$, of honest registered members, it returns a signature created by $id_b$.

The above notion is referred to as CPA-anonymity. When the oracle provides the additional functionality that, on receiving a valid signature and message, it returns the result of $\mathsf{Open }$ on the input, we call the strengthened notion CCA-anonymity [23].

• Traceability is defined by a game where an adversary corrupting the opener and arbitrary members attempts to create a signature that verifies correctly but yields invalid opening information that does not identify any registered member.

Definition 7

(Traceability) A group signature scheme is traceable if for any probabilistic polynomial-time adversary ${{\mathcal {A}}}$

$$\begin{aligned} \Pr \left[ \begin{array}{l} ({{ vk}}_{\mathrm{g}},{ sk}_{\mathrm{c}},{ sk}_{\mathrm{o}}) \leftarrow \mathsf{Setup }(1^\lambda ); \\ ( msg ,\pi ) \leftarrow {{\mathcal {A}}}^{{{\mathcal {O}}}}({{ vk}}_{\mathrm{g}}, { sk}_{\mathrm{o}})\\ (id, open ) \leftarrow \mathsf{Open }({ sk}_{\mathrm{o}}, msg ,\pi ) \end{array}: \begin{array}{l} 1 = \mathsf{Vrf }({{ vk}}_{\mathrm{g}}, m, \pi )\,\,\, \wedge \\ 0= \mathsf{Judge }({{ vk}}_{\mathrm{g}},\pi , msg ,id, open , reg ) \\ \end{array} \right] \end{aligned}$$

is negligible, where oracle ${{\mathcal {O}}}$ plays the role of the honest issuer in the protocol $\mathsf{Join }$.

• Non-frameability is defined by a game where an adversary corrupting the opener attempts to create a group signature on a message together with an opening of it that identifies a group member who never signed the message. The issuer is supposed to be honest in the sense that it honestly certifies association between uncorrupted members’ identities and their own public key. This is formalized by not allowing the adversary to write to $reg$.

Definition 8

(Non-Frameability) A group signature scheme is non-frameable if for any probabilistic polynomial-time adversary ${{\mathcal {A}}}$

$$\begin{aligned} \Pr \left[ \begin{array}{l} ({{ vk}}_{\mathrm{g}},{ sk}_{\mathrm{c}},{ sk}_{\mathrm{o}}) \leftarrow \mathsf{Setup }(1^\lambda ); \\ (m, \pi , id, open ) \leftarrow {\mathcal {A}}^{{\mathcal {O}}}({ sk}_{\mathrm{c}},{ sk}_{\mathrm{o}}) \end{array} : \begin{array}{l} 1 = \mathsf{Vrf }({{ vk}}_{\mathrm{g}}, m, \pi )\,\,\, \wedge \\ 1= \mathsf{Judge }({{ vk}}_{\mathrm{g}}, m, \pi , id, open , reg ) \wedge \\ id \in {{\mathcal {H}}} \wedge m \notin {{\mathcal {L}}}_{id}\\ \end{array} \right] \end{aligned}$$

is negligible where oracle ${{\mathcal {O}}}$ works as follows.

• On receiving a request, it invokes $\mathsf{Join }$ as a member with a new identity, $id$, and interacts with ${{\mathcal {A}}}$ playing the corrupt issuer. When the member-side protocol is successfully completed with $usk$ obtained, the oracle records $(id, upk )$ to $reg$ and $(id, usk )$ to ${{\mathcal {H}}}$, the list of honest users. (Note that $reg$ is not available to ${{\mathcal {A}}}$; also note that we assume that $upk$ is obtained by the successful interaction.)

• On receiving $id \in {{\mathcal {H}}}$, it returns corresponding $usk$ and removes the record from ${\mathcal {H}}$.

• On receiving $(id, msg )$, if $(id, usk ) \in {{\mathcal {H}}}$ for some $usk$, it returns a signature on $msg$ by using $usk$ and records $m$ to ${{\mathcal {L}}}_{id}$.

(The definition in [19] is slightly stronger in the sense that an adversary attempts to create a signature that, on opening, identifies a group member who actually did not create the signature, though the member may have signed the same message before. The stronger notion can be captured by modifying the definition to $( msg ,\pi ) \notin {{\mathcal {L}}}_{id}$.)

A technical difficulty arises when the group manager, Alice, issues a certificate to a group member, Bob. Alice signs Bob’s public key but for the sake of provable security she should be convinced of the independence of Bob’s key from anyone else’s. The independence is assured by implementing the protocol in a way that Bob can retrieve the certificate only when he knows some critical information. Thus, the protocol often uses zero-knowledge proofs of knowledge, which lose efficiency when composed concurrently. The issue of efficient concurrent join has been addressed in the literature. A single-round certification protocol that allows concurrent execution is sketched in [32]. In their framework, the join protocol is as simple as letting user Bob obtaining a certificate from Alice on Bob’s public key. When Bob signs a document, he first signs the document using his own key and then proves that the signature is correct with respect to a key certified by Alice. The proof has to be zero knowledge (thus hiding the public key and the certificate) and non-interactively so that it can be included in the signature. Such a proof of knowledge, however, is not easy to instantiate efficiently due to high complexity of the relation to prove. The first efficient instantiation in the random-oracle model is presented in [68]. Using structure-preserving signatures as Alice’s certificates and applying the Groth–Sahai proof system for proving Bob’s knowledge of a correct certificate, this framework can be efficiently instantiated without random oracles. In the following, we refine the framework by incorporating ideas from [55].

Let $\mathsf{SIG{auth} }$ and $\mathsf{SIG{mem} }$ be signature schemes, and let $\mathsf{NIWI }$ be a witness-indistinguishable proof-of-knowledge system that allows one to extract a witness by using a trapdoor.

Theorem 12

Group signature scheme $\mathsf{GSIG }$ is CPA-anonymous, traceable and non-frameable if $\mathsf{SIG{auth} }$ and $\mathsf{SIG{mem} }$ are $\mathrm{EUF-CMA }$ and $\mathsf{NIWI }$ is witness-indistinguishable and knowledge sound. Furthermore, $\mathsf{GSIG }$ allows to run the $\mathsf{GSIG }.\mathsf{Join }$ protocol concurrently.

Proof

CPA-anonymity follows directly from the (computational) WI property [59] of the proof system NIWI. For traceability, suppose that there is a valid signature $\pi$ on message $msg$. Due to knowledge soundness of NIWI, the opener can extract $({ vk}_{\mathrm{u}},\sigma _{{\mathrm{c}}},\sigma _{\mathrm{u}})$ from $\pi$, which satisfy $1 = \mathsf{SIG{auth} }.\mathsf{Vrf } ({ vk}_{\mathrm{c}},{ vk}_{\mathrm{u}},\sigma _{{\mathrm{c}}})$. If ${ vk}_{\mathrm{u}}$ does not point to any group member registered through $\mathsf{GSIG }.\mathsf{Join }$, $\sigma _{{\mathrm{c}}}$ is a valid forgery for $\mathsf{SIG{auth} }$, which contradicts EUF-CMA of $\mathsf{SIG{auth} }$. In more detail, this is shown by constructing a reduction to EUF-CMA that simulates the joining protocol by using the signing oracle of $\mathsf{SIG{auth} }$. Clearly, this is possible even if $\mathsf{GSIG }.\mathsf{Join }$ is executed concurrently with several members since the protocol consists of only one round of message flow between the issuer and the member. Thus, ${ vk}_{\mathrm{u}}$ allows tracing with concurrent execution of the join protocol. For non-frameability, suppose that the opener extracts $({ vk}_{\mathrm{u}},\sigma _{{\mathrm{c}}},\sigma _{\mathrm{u}})$ from a group signature on message $msg$. If $1 = \mathsf{SIG{mem} }.\mathsf{Vrf } ({ vk}_{\mathrm{u}}, msg ,\sigma _{\mathrm{u}})$ holds, but the owner of ${ vk}_{\mathrm{u}}$ has never signed $msg$, it is a valid forgery for $\mathsf{SIG{mem} }$, contradicting EUF-CMA of $\mathsf{SIG{mem} }$.$\square$

By instantiating $\mathsf{SIG{auth} }$ with our structure-preserving signature scheme $\mathsf{CSIG }$ (given on page 30) and $\mathsf{NIWI }$ with the GS proof system, we can instantiate the above generic construction efficiently. Furthermore, using $\mathsf{CSIG }$ for $\mathsf{SIG{auth} }$ allows the inclusion of a human-readable “warrant” in $\sigma _{{\mathrm{c}}}$ so that the signing policy given to a group member is explicit. A warrant is a written policy that defines validity of signatures, e.g., specific period of time in which the signature is valid. Since $\mathsf{CSIG }$ has constant-size signatures, this extension can be done without impacting the size of the group signature (except for the warrant itself) at all.

We assess the efficiency in the setting $\Lambda = \Lambda _{\mathsf{sym }}$ as follows. Let $\mathsf{SIG{mem} }$ be a signature scheme whose verification key ${ vk}_{\mathrm{u}}$ and signature $\sigma _{\mathrm{u}}$ consist of $\alpha$ and $\beta$ group elements, respectively. Let $\gamma$ be the number of group elements needed to prove relation $1 = \mathsf{SIG{mem} }.\mathsf{Vrf } ({ vk}_{\mathrm{u}}, msg ,\sigma _{\mathrm{u}})$ including GS commitments for ${ vk}_{\mathrm{u}}$ and $\sigma _{\mathrm{u}}$. Regardless of the size of ${ vk}_{\mathrm{u}}$ to be certified, our $\mathsf{SIG{auth} }$ outputs $\sigma _{{\mathrm{c}}}$ of size $7$. Since $4$ out of the $7$ elements in $\sigma _{{\mathrm{c}}}$ can be perfectly randomized and given in the clear (as observed in Sect. 5.1), we need only $3$ GS commitments to prove relation $1 = \mathsf{SIG{auth} }.\mathsf{Vrf } ({ vk}_{\mathrm{c}},{ vk}_{\mathrm{u}},\sigma _{{\mathrm{c}}})$, which consists of two one-sided pairing-product equations and costs 6 elements in a proof. (Commitments of ${ vk}_{\mathrm{u}}$ are already included in $\gamma$.) In total we have $(\text {Group Sig Size}) = 19 + \gamma$. For comparison, we propose to instantiate $\mathsf{SIG{auth} }$ by using a signature scheme in [38], which has $9 \alpha + 4$ elements in $\sigma _{{\mathrm{c}}}$ and $3 \alpha + 3$ one-sided and $3 \alpha$ double-sided pairing-product equations in $\mathsf{SIG{auth} }.\mathsf{Vrf }$. In that case, the size of a group signature is $(\text {Group Sig Size}) = 63 \alpha + 21 + \gamma$.

If we instantiate $\mathsf{SIG{mem} }$ with the fully EUF-CMA Boneh-Boyen signature scheme [22], ${ vk}_{\mathrm{u}}$ consists of $\alpha = 3$ group elements (including the bases). A signature consists of one group element and one scalar value, but the scalar value is totally random and independent of the verification key. So we have $3+1$ GS commitments in proving $1 = \mathsf{SIG{mem} }.\mathsf{Vrf } ({ vk}_{\mathrm{u}}, msg ,\sigma _{\mathrm{u}})$. The verification predicate consists of a double-sided pairing-product equation, which yields 9 group elements in a proof. In total, we have $\gamma = 21$ and a group signature consists of $40$ group elements and 1 scalar value.

Table 2 summarizes some efficient group signature schemes that provide CPA-anonymity in the standard model under non-interactive assumptions. Our construction $\mathsf{GSIG }$($\mathsf{CSIG }$+BB[22]) yields a signature that contains $10$ more group elements than that of [55]. This is the price for achieving the concurrent join property and allowing a simple and modular security argument without dedicated assumptions. For comparison, we also consider the case where a signature scheme in [38] is used as $\mathsf{SIG{auth} }$. With the same setting ($\alpha = 3$, $\gamma = 21$), the signature size results in $231\,(=63 \times 3 + 21 + 21)$ group elements and $1$ scalar value.

Table 2 Summary of efficiency and properties of group signature schemes with CPA-anonymity

Finally, we remark that CCA-anonymity is obtained by following the approach in [55], which uses a strong one-time signature scheme and a selective-tag CCA-secure tag-based public key encryption scheme. A decryption key of the tag-based encryption is given to the opener, and the public key is published. When a member issues a signature, ${ vk}_{\mathrm{u}}$ is encrypted by the tag-based encryption under a one-time verification key as a tag. Then, a NIZK is generated to prove that the ciphertext decrypts to the same value, i.e., ${ vk}_{\mathrm{u}}$, committed for NIWI proof $\pi$. The one-time key is used to sign $\pi$, the ciphertext and the NIZK proof. By using the same instantiation as in [55], this strengthening costs 15 extra group elements in a signature. (Committing to 3 random coins used in tag-based encryption costs $3 \times 3$ elements, and proving 3 relations in multi-exponentiations costs $3 \times 2$ elements.) Accordingly, we have a CCA-anonymous group signature scheme with concurrent join whose signature consists of $55 ({=}\,40+15)$ group elements and one scalar value.

7.2 Round-Optimal Blind Signatures

A blind-signature scheme $\mathsf{BS }$ allows a user to obtain signatures on messages which remain hidden from the signer. It is defined by five algorithms $\mathsf{BS } = \mathsf{BS }.$ $\{\mathsf {Setup}, \mathsf{Key }, \mathsf{User },\mathsf{Signer }, \mathsf{Vrf }\}$, where $\mathsf {Setup}$, on input $1^\lambda$, generates the common parameters $gk$; $\mathsf{Key }$, on input $gk$, generates a key pair $({ vk},{ sk})$; $\mathsf{User }$ is a signature-request algorithm, taking input $gk ,{ vk}$ and a message, which interacts with the signer-side algorithm $\mathsf{Signer }$, having input ${ sk}$, as a signature-generation protocol; $\mathsf{BS }.\mathsf{Vrf }$ that verifies a signature on a message w.r.t. $gk$ and ${ vk}$. The notion of completeness is defined as for ordinary digital signature schemes; that is, when $gk \leftarrow \mathsf {Setup}(1^\lambda )$ and $({ vk},{ sk})\leftarrow \mathsf{Key }( gk )$ then for every message $msg$ and every $\sigma$ obtained by running $\mathsf{User }( gk ,{ vk}, msg )\leftrightarrow \mathsf{Signer }({ sk})$ we have: $1 \leftarrow \mathsf{Vrf }( gk ,{ vk}, msg ,\sigma )$.

A blind-signature scheme $\mathsf{BS }$ is round-optimal if in the signature-generation protocol there is only one round of communication: $\mathsf{User }$ sends a message to $\mathsf{Signer }$ and the latter sends one message back; this means that $\mathsf{Signer }$ is a (stateless) algorithm that takes a secret key ${ sk}$ and a message $msg _\mathsf{U }$ from $\mathsf{User }$ and outputs a message $msg _\mathsf{S }$ that is given to $\mathsf{User }$, which outputs a signature $\sigma$.

The two standard security notions are unforgeability and blindness as defined in, e.g., [44, 61, 84]. Blindness means that no adversarial signer can associate a valid signature to an execution of the signature-generation protocol. Unforgeability states that no adversarial user can obtain more valid signatures than the number of completed signature-generation protocol executions.

Definition 9

(Blindness) A (round-optimal) blind-signature scheme satisfies blindness if for any probabilistic polynomial-time adversary ${{\mathcal {A}}}$

$$\begin{aligned} \Pr \left[ \begin{array}{l} b\leftarrow \{0,1\};\, gk \leftarrow \mathsf{Setup }(1^\lambda );\, ({ vk},m_0,m_1,{ st}_{{\mathcal {A}}}) \leftarrow {{\mathcal {A}}}( gk ) \\ \text {For i=b,1-b do} \\ \ \ ( msg _\mathsf{U },{ st}_\mathsf{U }) \leftarrow \mathsf{User }( gk ,{ vk},m_{i})\\ \ \ ( msg _{\!{{\mathcal {A}}}},{ st}_{{\mathcal {A}}}) \leftarrow {{\mathcal {A}}}({ st}_{{\mathcal {A}}}, msg _\mathsf{U });\, \sigma _{i} \leftarrow \mathsf{User }({ st}_\mathsf{U }, msg _{\!{{\mathcal {A}}}}) \\ \text {If}\,\, \sigma _0=\bot \,\,\hbox {or} \,\, \sigma _1=\bot \,\, \hbox {then}\,\, (\sigma _0,\sigma _1):=(\bot ,\bot ) \\ b^{\star } \leftarrow {{\mathcal {A}}}({ st}_{{\mathcal {A}}},(\sigma _0,\sigma _1)) \end{array}: \begin{array}{l} b^{\star } = b\end{array} \right] - \frac{1}{2} \end{aligned}$$

is negligible.

Definition 10

(Blind-Signature Unforgeability) A (round-optimal) blind-signature scheme is unforgeable if for any probabilistic polynomial-time adversary ${{\mathcal {A}}}$

$$\begin{aligned} \Pr \left[ \begin{array} {l} gk \leftarrow \mathsf{Setup }(1^\lambda ); \ ({ vk}, { sk}) \leftarrow \mathsf{Key }( gk )\\ ((m^{\star }_1, \sigma ^{\star }_1),\ldots , (m^{\star }_q,\sigma ^{\star }_q)) \\ \leftarrow {{\mathcal {A}}}^{\mathsf{Signer }( sk , \cdot )^{(q-1)}}( vk ) \end{array}: \begin{array} {l}m^{\star } \ne m^{\star }_j \text {~for all~} i\ne j \\ 1 \leftarrow \mathsf{Vrf }( vk , m^{\star }_i, \sigma ^{\star }_i)\\ \text {~~for~} 1\le i\le q\end{array} \right] \end{aligned}$$

is negligible, where the adversary is allowed $q-1$ oracles calls to $\mathsf{Signer }$.

Fischlin [43] gives a generic construction for concurrently executable blind-signature schemes with optimal round complexity in the common reference string (CRS) model. The construction relies on commitment, encryption and signature schemes and generic NIZK proofs for NP-languages. In the signature-issuing protocol, the user first sends a commitment to the message to the signer, who responds with a signature on the commitment. The user then constructs the blind signature as follows: She encrypts the commitment and the signature and adds an NIZK proof that the signature is valid on the commitment and that the committed value is the message.

Following [61], Abe and Ohkubo [10] replace the NIZK proof in Fischlin’s construction by a witness-indistinguishable proof and concretely suggest Groth–Sahai (GS) proofs. (Note that GS commitments on group elements can be “decrypted” using the extraction key.) To be compatible, the signature scheme must have messages and signatures consisting of group elements and verification must amount to evaluating pairing-product equations. However, they only mention the highly inefficient scheme from [54] as a feasibility result and leave open the problem of an efficient construction. Structure-preserving signatures satisfy all the compatibility requirements and enable thus an efficient instantiation of round-optimal blind signatures; it suffices to construct a commitment scheme such that commitments lie in the message space of the signature and correct opening is verifiable by pairing-product equations.

We directly construct a scheme based on $\mathsf{ASIG{} }$ (Sect. 6.1) which has smaller blind signatures than an instantiation of the generic construction. This is because in the end of our issuing protocol the user holds a signature on the actual message rather than on a commitment to it. To make this possible, the user sends a randomization of the message to the signer in addition to the commitment. From this, the signer makes a “pre-signature” and sends it to the user, who, knowing the randomizer, can turn it into an actual signature on the message. The blind signature is then a GS proof of knowledge of a signature on the message (rather than a commitment), which avoids a proof that the commitment opens to the message.

In more details, given parameters $(\Lambda ,F,K,T)$ a user who wants to obtain a blind signature on $(M,\tilde{N})$ chooses a random $\rho \leftarrow {{\mathbb {Z}}}_p$, and blinds $M$ by the factor $T^\rho$. In addition to $U:=T^\rho \cdot M$, she sends a GS proof of knowledge of $(M,\tilde{N})$ and $(G^\rho ,\tilde{G}^\rho )$. The signer now formally produces a “signature” on $U$, for which we have $A=(K\cdot T^r\cdot U)^{1/(x+c)}=(K\cdot T^{r+\rho }\cdot M)^{1/(x+c)}$; thus, $A$ is the first component of a signature on $(M,\tilde{N})$ with randomness $r+\rho$. The user can complete the signature by adapting randomness $r$ to $r+\rho$ in the other components. The blind signature is a GS proof of knowledge of this signature.

Note that it is the particular form of signatures of $\mathsf{ASIG{} }$ that allow turning a signature on a “half-message” $U$ into a signature on any $M= T^{-\rho }$, if one knows $\rho$. This does not contradict unforgeability, since the user does not obtain a signature on $U$ (unless $U=M$), since $U$ is not an element of the message space $\mathcal {DH}$. And to produce $(U,\tilde{G}^{\log _G U})\in \mathcal {DH}$, the user would have to break AWF-CDH.

The protocol is correct: The signer sends $A=(K\cdot T^r\cdot U)^\frac{1}{x+c}=(K\cdot T^{r+\rho }\cdot M)^\frac{1}{x+c}$, $B=F^c$, $\tilde{D}=\tilde{G}^c$, $R'=G^r$, $\tilde{S}'=\tilde{G}^r$ and the user sets $R:=R'\cdot P=G^{r+\rho }$ and $\tilde{S}:=\tilde{S}'\cdot \tilde{Q}=\tilde{G}^{r+\rho }$, which makes it a valid signature on $(M,\tilde{N})$ with randomness $r+\rho$.

The round complexity of the scheme is optimal [43]. The user message is in ${{\mathbb {G}}}^{17}\times \tilde{{{\mathbb {G}}}}^{16}$, the signer message in ${{\mathbb {G}}}^3\times \tilde{{{\mathbb {G}}}}^2$ and a blind signature is in ${{\mathbb {G}}}^{18}\times \tilde{{{\mathbb {G}}}}^{16}$. Note that the scheme remains automorphic, since commitments and proofs are composed of group elements that are verified by checking pairing-product equations and the verification keys and messages are those from $\mathsf{ASIG }$. It is the automorphic property of the scheme that allowed its use to implement (blinded) certification chains in the construction of non-interactively delegatable anonymous credentials in [46].

Theorem 13

Blind-signature scheme $\mathsf{BS }$ is unforgeable and blind if ADH-SDH and SXDH hold for ${\mathcal {G}}$.

Proof

Blindness. In the blindness game, we choose a random $b\leftarrow \{0,1\}$, which the adversary must guess. After setting up $gk$ we are given ${ vk},m_0$ and $m_1$ by the adversary and run $\mathsf{User }$ for $m_b$ and for $m_{1-b}$. If both executions succeed, yielding $\pi _b$ and $\pi _{1-b}$, the adversary is given $(\pi _0,\pi _1)$ and must guess $b$.

We modify the game in Definition 9 by replacing $\Sigma _{\mathsf{GS } }$ by a simulated CRS, which leads to perfectly WI commitments and proofs. This modification is indistinguishable by SXDH. We claim that in this modified game the adversary’s probability of guessing $b$ is exactly $\frac{1}{2}$, because neither what is sent by $\mathsf{User }$ nor the final signatures contain any information about $b$.

First consider $(U, \phi )$ given to the adversary during the signature-generation protocol. To see that $(M,\tilde{N})$ is perfectly hidden, observe that for every possible $M\in {{\mathbb {G}}}$, there exists a (unique) value $\rho \in {{\mathbb {Z}}}_p$ that satisfies $U = T^{\rho } \cdot M$. In other words, for every $(M,\tilde{N})\in \mathcal {DH}$, there exist uniquely determined $(P,\tilde{Q})$ which satisfy the equations in (51). Since by perfect WI, the proof $\phi$ is independent of its witness $(M,\tilde{N},P,\tilde{Q})$, $(U,\phi )$ information-theoretically hides the bit $b$.

If the adversary did not produce two valid (pre-signatures), it receives $(\bot ,\bot )$ at the end. Otherwise, the experiment computes two tuples $(A,B,\tilde{D},R,\tilde{S})$, which satisfy (52) and gives the adversary two GS proofs of knowledge of them. Again by perfect WI, the proofs are distributed as if they were computed using a random witness (in this case a fresh signature); the proofs are thus independent of the signature-generation protocol.

Unforgeability. We show that, after running the protocol $q-1$ times with an honest signer, no adversary can output $q$ different messages and valid blind signatures on them. To do so, we reduce unforgeability to the security of the signature scheme $\mathsf{ASIG{} }$, which follows from ADH-SDH and AWF-CDH (the latter being implied by SXDH). Given parameters $gk_\mathsf{ASIG } :=(\Lambda ,F,K,T)$ and a public key $(X,\tilde{Y})$ for $\mathsf{ASIG{} }$, we first generate a key $\Sigma _{\mathsf{GS } }$ for the GS proof system as specified by $\mathsf {Setup}$, but together with extraction key $ek$. We run the adversary on ${\Sigma _{}}=(gk_\mathsf{ASIG },\Sigma _{\mathsf{GS } })$. Whenever ${\mathcal {A}}$ sends a request $(U,\phi )$, we extract $(M,\tilde{N},P,\tilde{Q})$ from $\phi$ using $ek$. Soundness of the proof ensures that by (52) there exist $m,\rho \in \mathbb {Z}_p$ such that $M=G^m,\tilde{N}=\tilde{G}^m,P=G^\rho ,\tilde{Q}=\tilde{G}^\rho$ and $U=T^\rho \cdot M$. We then send $(M,\tilde{N})$ to the signing oracle of $\mathsf{ASIG{} }$ and receive a signature $(A,B,\tilde{D},R,\tilde{S})$. We return to the adversary $(A,B,\tilde{D},R'\!:=\!R\cdot P^{-1},\tilde{S}'\!:=\!\tilde{S}\cdot \tilde{Q}^{-1})$. This perfectly simulates $\mathsf{Signer }$: Since the oracle produced a correct signature, there exist $c$ and $\hat{r}$ such that $B=F^c$, $\tilde{D}=\tilde{G}^c$, $R=G^{\hat{r}}$, $\tilde{S}=\tilde{G}^{\hat{r}}$ and $A=(K\cdot T^{\hat{r}}\cdot M)^\frac{1}{x+c}=(K\cdot T^{\hat{r}-\rho }\cdot U)^\frac{1}{x+c}$. Thus, $R'=G^{\hat{r}-\rho }$ and $\tilde{S}'=\tilde{G}^{\hat{r}-\rho }$, which corresponds to a real reply by the $\mathsf{Signer }$ oracle using randomness $c$ and $r:=\hat{r}-\rho$ (which is uniform).

After at most $q-1$ requests, the adversary outputs $q$ valid signatures on different messages. Among those messages, there exist at least one message that was not sent to the $\mathsf{ASIG{} }$ oracle. We extract the signature corresponding to that message using $ek$. By the soundness of the GS proof, it is a valid signature and can thus be returned as a valid forgery for $\mathsf{ASIG{} }$.$\square$