Introduction

Nowadays, many people worldwide have demonstrated the need to know their personal records regarding health, sports performance, or even the combination of both during sports training routines. This has been possible due to the implementation of ergonomic devices based on electronic materials and sensing technology innovations. Some representative utilities of these devices are, for example, human motion monitoring [1, 2], healthcare [3], gesture recognition [4], tactile sensors [5], and even the development of soft robots with sensory capabilities [5, 6]. To develop these types of sensors, different fabrication methods have been used such as 3D printing [7], coating, spinning, chemical vapor deposition, lithography technologies, laser ablation and transfer methods [4, 8, 9]. Now it is known that depending on several factors such as the synthesis method, structural design, the conductive particles and their guest polymeric matrix, the flexible strain sensors’ working mechanisms could be due to piezoresistive effects, geometric effects, crack propagation, disconnection, tunneling effect or a combination of some of them [4, 10].

It is clear that the interest in flexible strain sensors is increasing nowadays, and a notable number of works have studied the development, characterization and application of different types/shapes and measurement mechanisms of such sensors [4, 11]. Flexible strain sensors are usually made of elastomer, like PDMS, and different conductive particles such as platinum [12], gold [13], carbon black [14], graphene/graphene oxide [15, 16], carbon nanotubes[17, 18], multiwalled carbon nanotubes [8, 9] or a combination of some of them like carbon nanotubes with graphene[19], palladium with graphene oxide [16], or carbon nanotubes with Mxene [20]. Besides PDMS, other polymeric matrices have been explored as well to develop these strain sensors, including natural fibers such as cotton coated with a composite based on PTFE/water, Capstone ST-110 with carbon nanotubes [21] or even medical elastic bands coated with self-segregated carbon nanotubes [18]. The variety of applications achieved by these flexible sensors are large, some notable examples are: gas selectivity and separation [14], compressive, shear, and torsional load sensors [12], motion detection of human joints, facial gesture [8, 13, 17, 19] and medical signals during sport training routines on humans, [20] among others.

Although significant advances have recently been made in the development and application of flexible strain sensors, there still remains the need to understand their work mechanism and consequently improve their stability, sensitivity, response time and sensing range of these sensors based on PDMS and conductive nanoparticles. A considerable cumulus of work has been addressed to study different types of flexible strain sensors. To the best of our knowledge, nobody has studied experimentally and numerically the electrical and mechanical responses of a flexible strain sensor based on a carpet of conductive MWCNT’s deposited over a S-shaped pattern within a PDMS matrix. Therefore, the main purpose of this work was to generate a free-standing MWCNT’s S-pattern as a conductive circuit embedded between PDMS layers to obtain a low-cost, flexible strain sensor which will be experimentally and numerically evaluated to get a better understanding of its mechanical and electrical behaviors under cycling uniaxial loads.

Materials and methods

Materials

Dow Corning Sylgard 184 Poly(dimethylsiloxane) (PDMS) in a 10:1 ratio was used as the flexible polymeric base of the strain sensor. Multi-walled carbon nanotubes (MWCNT’s) 6-9 nm in diameter and 5 \(\mu \)m of length were used to fabricate the conductive pattern of the sensors (MWCNT’s were purchased from Sigma Aldrich, St. Louis, MO, USA, CAS:308068-56-6). Both PDMS and MWCNT’s were used as received.

Methods

fabrication of the flexible strain sensor

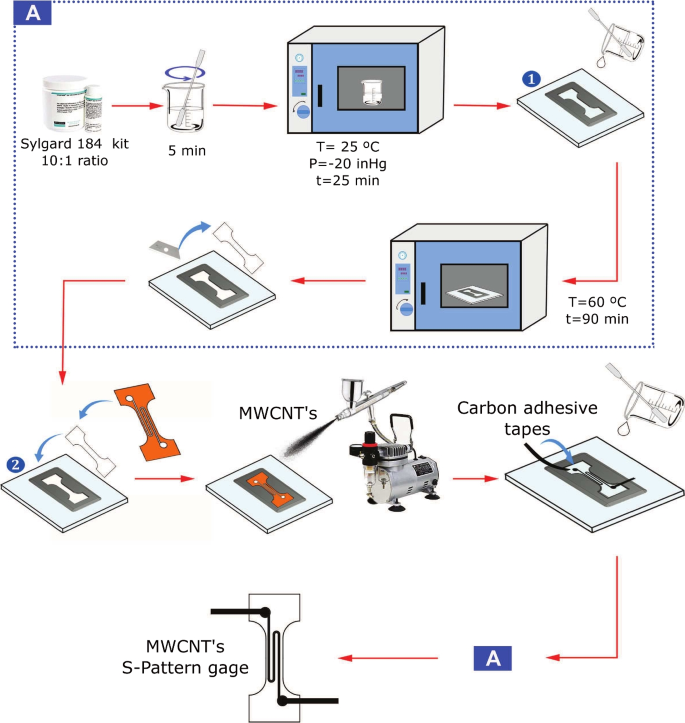
The explanation of the fabrication protocol is illustrated in Fig. 1. Using the Sylgard 184 kit, the PDMS part A (pre-polymer) and PDMS part B (curing reagent) were weighted, preserving a 10:1 ratio. Then parts A and B were mechanically stirred for 5 minutes at room temperature. The mixture was degassed in a vacuum chamber having a pressure of -67 kPa for 25 minutes at room temperature. Subsequently, the mixture was poured into a PLA 3D-printed mold with a specific geometry following the D1708 ASTM standard. The PLA mold was previously supported and fixed on glass using double-sided adhesive tape. The mixture within the mold was cured in an oven at 60 \(^\circ \)C for 90 minutes. Then the cured samples exhibiting the geometry of a dog-bone-shaped specimen (with thickness around 500 \(\mu \)m) were carefully detached and transferred to another but deeper 3D-printed PLA molds. Next, we put over the first layer of the dog-bone-shaped PDMS a mask made of adhesive vinyl having the same dog-bone shape but now including a centered hollow channel with an S-pattern. This pattern works as a strain gage. The masks were fabricated using the laser cutting module of the ZMorph FAB multifunctional. Later, 1 mg of MWCNT’s were dissolved in 10 mL of isopropyl alcohol and sonicated for 5 minutes; subsequently, this dissolution was poured into an Iwata airbrush (HP-C NCE model). Then, 1mL of the MWCNT’s dissolution was sprayed on the PDMS surface, with the mask and the airbrush connected to an oil-free air compressor working at 138 kPa. Thus, after 100 cycles of deposition, a conductive S-pattern of MWCNT’s was obtained. After total evaporation of the isopropyl alcohol, we carefully detached the vinyl mask. Next, the conductive MWCNT path terminals were connected to two adhesive carbon tape strips, which were later used to monitor the electrical resistance. After this, a second layer of PDMS was collocated on top of the first layer, sandwiching the MWCNT’s thin path. This was done by pouring liquid PDMS (10:1 ratio) into the mold, covering the first cured PDMS layer, the MWCNT conductive pattern, and carbon strips. Finally, the whole set was cured (temperature 60 \(^\circ \)C for 90 minutes) to encapsulate the MWCNT’s conductive path with the reticulated elastomer, the former being the active part of the flexible strain sensor.

Fig. 1
figure 1

Flexible strain sensor fabrication process. The rectangle made with the blue dashed line depicts the PDMS 10:1 ratio preparation and the process of obtaining the test sample in a dog bone shape. Besides, here we show the process of deposition of MWCNT’s to get the conductive strain gage pattern of the sensor

Full size image

Uniaxial tensile assays

The uniaxial tensile assays were conducted in a custom-designed mechanical tester. It consists of a load frame, a motorized linear stage (model MTS50-Z8 from Thorlabs), a miniature load cell with a capacity of 111 N (model 31 series from Honeywell), and PLA 3D-printed grips. The load frame was fabricated in 28 mm squared aluminum profiles which were vertically fixed on an aluminum breadboard (MBH3060/M 300x600 mm from Thorlabs). The MTS50-Z8 was used as a mechanical actuator providing controlled displacement ranging from 0-50 mm, and it was mounted on the vertical profiles. The upper grip was coupled to the MTS50-Z8 mechanical actuator by L-Type support. Meanwhile, the load cell and lower grip were mounted in a transversal squared aluminum profile which was also fixed to the vertical profiles. The mechanical actuator, the load cell, and the grips were carefully aligned, preserving a vertical axial axis. The flexible strain sensor was fixed between the grips, and its carbon strips were connected to a Tektronix multimeter model DMM4050 in order to register the electrical resistance changes as the uniaxial load acts on the flexible strain sensor. Notice that a second multimeter (HP model 34401A) was used to acquire the conditioned and amplified load cell signal. Thus, time, displacement, and force data were acquired synchronously by using a virtual instrument specially programmed in LabVIEW, which involves the control of the MTS50-Z8 mechanical actuator and the acquisition of the signals during the experiment.

The elastic constants of the flexible strain sensor made of PDMS were determined by non-linear fitting of the stress as a function of the elongation ratio data that were obtained from the uniaxial tensile experiments. The non-linear mechanical response of PDMS required the use of Ogden’s model [22] to mimic the mechanical behavior of the sensor. Hence the stress (\(\sigma \)) is determined with Eq. 1. Here \(\lambda \) is the elongation ratio calculated from engineering strain (\(\varepsilon \)) as \(\lambda =\varepsilon +1\); meanwhile, \(\mu _{i}\) and \(\alpha _{i}\) are constants that are used to calculate the shear elastic modulus (G) through the Eq. 2. The index (n) indicates the order of Ogden’s model. Assuming that PDMS presents a rubber-like mechanical behavior and has a Poisson ratio of \(\nu =0.5\), the following relation between elastic constants can be used: E= 2G(1+\(\nu \)), giving Eq. 3.

$$\begin{aligned} \sigma = \sum _{i=1}^{n} \mu _{i}\bigg (\lambda ^{\alpha _{i}}-\lambda ^{-\frac{\alpha _{i}}{2}}\bigg ) \end{aligned}$$
(1)
$$\begin{aligned} G= \frac{1}{2}\sum _{i=1}^{n} \mu _{i}\alpha _{i} \end{aligned}$$
(2)
$$\begin{aligned} E= 3G \end{aligned}$$
(3)

Once the elastic modulus was first determined by single load uniaxial tensile assay, uniaxial tensile load/unload cycles were applied. The first three cycles were applied using three different elongation ratios (1.25, 1.35, and 1.45) to observe the sensors’ initial mechanical and electrical behavior. The following seven cycles reached an elongation ratio of 1.45. After these 10 cumulative cycles, the next 10 cycles were applied using a 1.45 elongation ratio. This was done to register the influence of cycles on the mechanical and electrical behavior of the flexible strain sensors. To complement the experiments, numerical simulations were conducted to distinguish between the macroscopic (changes in gage’s geometry) and micro/nanoscopic (nanotube orientation changes, tunneling) effects on the electrical resistance changes. To capture the orientation of the nanotubes, we used simple theoretical concepts such as the order parameter [23] and a straightforward equation of state based on the macroscopic strain \(\varepsilon \). These theoretical concepts are discussed in the results section.

Numerical simulations

Numerical simulations were conducted in COMSOL Multiphysics to know the exact ohmic resistance due to geometrical changes (increase in length and decrease of cross-section) of the MWCNT S-pattern. The 3D geometry of the uniaxial test samples, following the D1708 ASTM standard, was used here. The numerical version of the sensor was made of 14,000 triangular prism elements, and a dedicated spiral-shaped channel was computationally made to simulate the path of MWCNT. Besides, the elastic constants determined for PDMS in uniaxial tensile assays were used in the simulations. Since PDMS is highly incompressible, we choose a mixed formulation in the mechanical stress equations to avoid volumetric locking phenomena, so the deviatoric and volumetric parts of the strain were treated separately [24] (if this is not done, unrealistic lateral displacements of the whole numerical geometry in the final results are detected). We also imposed symmetry conditions on appropriate surfaces to stabilize the simulations and so only 1/8 of the whole geometry was simulated thanks to symmetry. The numerical problem is then to find the sensor’s equilibrium stress field given a uniaxial displacement \({\textbf {u}}\) on the axial faces. The central equation to solve is the conservation of momentum expressed as:

$$\begin{aligned} \nabla \cdot \left( F \mathbb {S} \right) ^{T}=0 \end{aligned}$$
(4)

where the deformation tensor is \(F={\textbf {I}}+\nabla {\textbf {u}}\) and the stress \(\mathbb {S}=\partial {W}/\partial {\mathcal {C}}\) (second Piola-Kirchhoff stress tensor) is obtained by deriving the strain energy function W with respect to the conjugate of \(\mathbb {S}\), that is, the Green-Lagrange strain \(\mathcal {C}\). The strain energy function is, in turn, defined in terms of the principal stretch elongation ratios, according to Ogden [22]. In Ogden’s model, W is written as:

$$\begin{aligned} W=\sum _{i} \frac{\mu _{i}}{\alpha _{i}} \left( \overline{\lambda }_{1}^{\alpha _{i}}+\overline{\lambda }_{2}^{\alpha _{i}}+\overline{\lambda }_{3}^{\alpha _{i}}-3 \right) +\frac{1}{2}K(J-1)^{2} \end{aligned}$$
(5)

where \(\lambda _{j}\) are the principal stretch elongation ratios, K is the bulk modulus, \(J=det(F)\) and \(\overline{\lambda }_{j}=J^{-1/3}\lambda _{j}\). The derivatives with respect to \(\mathcal {C}\) can be worked out using the chain rule and the following expressions:

$$\begin{aligned} \frac{\partial \lambda _{i}}{\partial \mathcal {C}}=\frac{1}{2\lambda _{i}} \hat{{\textbf {N}}}_{i}\otimes \hat{{\textbf {N}}}_{i} \quad ; \frac{\partial {J}}{\partial \mathcal {C}}=\frac{J}{2}\mathcal {C}^{-1} \end{aligned}$$
(6)

where \(\hat{{\textbf {N}}}_{i}\) are the eigenvectors of each principal stretch elongation ratio.

Notice that since in the numerical simulations we obtain the full stress field inside the sensor and on its boundaries, an average procedure has to be done in order to compare the numerical values with the single stress value obtained experimentally. The experimental stress is calculated through the load cell transducer values divided by the sample’s transversal cross-section area, as previously described in the uniaxial tensile assays section.

Results

Morphological and structural analysis of the strain sensors

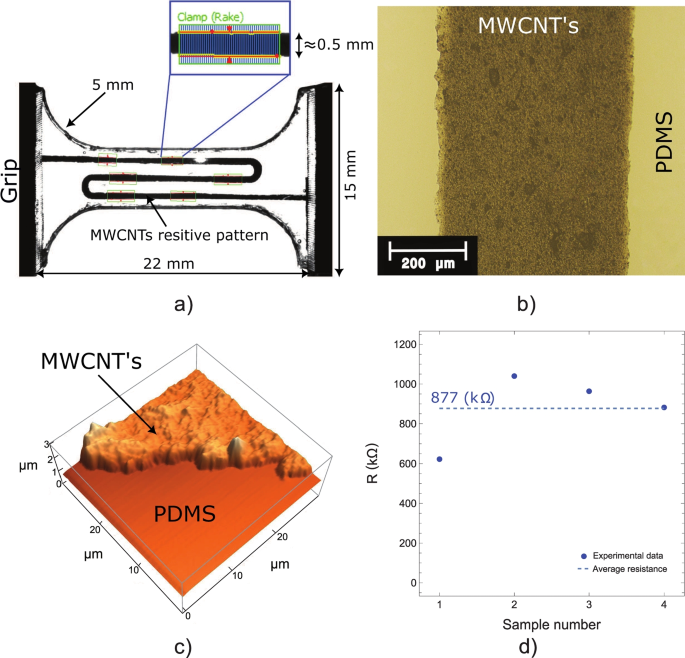
Figure 2 shows the main features of the resistive-strain gage sensor based on a MWCNT’s S-pattern embedded within PDMS. Figure 2 a) depicts the shape of the sensor; its design was based on the D1708 ASTM standard that contemplates the well-known dog-bone shape of a uniaxial tensile specimen. Thus, the specimen’s length, width, and thickness were 38, 15 and 2 mm, respectively, while the radius of curvature was 5 mm and the distance between grips was 22 mm. The width of the MWCNT’s resistive pattern was 500 ±25 \(\mu \)m according to the clamp rake tool from the measurements performed with vision assistant software (NI); in addition, it was corroborated through optical microscopy as shown in Fig. 2 b). The thickness of the MWCNT’s resistive pattern was measured through atomic force microscopy, as shown in Fig. 2 c). The average value of the thickness was 1.1 ±0.2 \(\mu \)m and the average of the Root Mean Square roughness (Sq) value was 320 nm. Once the AFM measurements were conducted, the resistive MWCNT’s S-pattern was embedded within PDMS with carbon-tape strips added as connectors for electrical measurements with a multimeter. The initial values of the resistance of the MWCNT’s S-pattern averaged \(R_{0}=877\pm 180 k\Omega \). Here the difference of the resistance initial values between samples could be associated with the density, dispersion, and orientation of the MWCNT’s along the MWCNT’s S-pattern. The individual values of the electrical resistance in 4 different fabricated sensors are shown in Fig. 2 d).

Fig. 2
figure 2

Main physical features of the embedded MWCNT’s circuit path within a PDMS uniaxial tensile sample. a) Digital image analysis to determine the width of the MWCNT’s circuit path, b) Top view of the MWCNT’s circuit path within a PDMS uniaxial tensile sample obtained by optical microscopy. c) AFM image showing the border of the MWCNT’s circuit path sprayed on PDMS membrane and d) Initial values of electrical resistance for different fabricated sensors

Full size image

Mechanical and electrical response under uniaxial tensile load

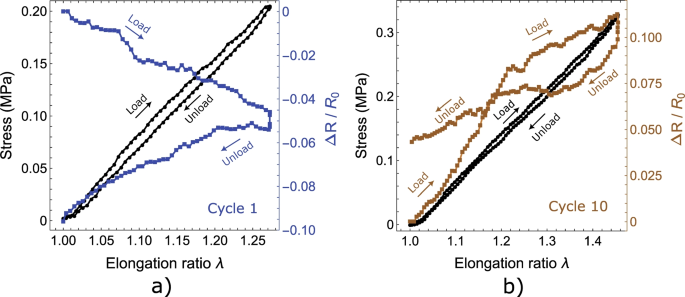
The mechanical and electrical behavior of the MWCNT’s resistive strain sensors were experimentally tested under uniaxial stress conditions. Figure 3 a) shows the mechanical response of the MWCNT’s resistive strain sensor embedded within PDMS. Here is shown that the same sensor was cycled 10 times using different elongation ratios. The three first cycles (initial cycles) were applied using \(\lambda \)=1.25, \(\lambda \)=1.35, and \(\lambda \)=1.45; subsequently, the number of cycles increased until reached 10 cycles using an elongation ratio of \(\lambda \)=1.45; their corresponding axial stress was 0.32 MPa. Regarding the mechanical response of the sensors, we observe that the PDMS presented a low non-linear behavior for the used elongation ratios, which were previously mentioned. Similar curves were obtained for three more samples; thus, the seven repetition cycles were averaged and shown in 3 b). Considering these average data, a first order Ogden model was used to obtain their mechanical models and the elastic modulus as shown in Table 1. In these cases, we obtained an average Elastic modulus of 0.69 ±0.02 MPa. The stress vs. elongation curves demonstrate acceptable repeatability of the MWCNT’s resistive strain sensors’ mechanical response under cycling and even between samples.

Fig. 3
figure 3

Mechanical and electrical responses of the MWCNT’s resistive strain gage. a) Stress vs. elongation ratio curves after 10 cycles of load using the same specimen. b) Non-linear model fitting using a first-order Ogden’s model for different specimens, c) Electrical resistance response of the MWCNT’s resistive strain as a function of the elongation ratio showing the first 10 cycles in the same specimen, and d) Electrical resistance average behavior considering 4-10 cycles for different specimens or samples

Full size image
Table 1 First-order Ogden models and their corresponding parameters to calculate the elastic modulus of the PDMS-MWCNT’s resistive strain sensors
Full size table
Fig. 4
figure 4

Gage factor of PDMS-MWCNT’s resistive strain sensors. a) Gage factor for the initial slope, b) Gage factor for the final slope

Full size image
Fig. 5
figure 5

Mechanical and electrical behavior of PDMS-MWCNT’s resistive strain sensors under load and unload cycling applied on the same sensor, a) Initial cycle b) cycle number 10

Full size image

Now, regarding the electrical response of the PDMS-MWCNT’s resistive strain sensors, we present the curves of the changes of electrical resistance \(\frac{\Delta R}{R_0}\) as a function of the elongation ratio (where \(\Delta R= R-{R_0}\)); Fig. 3 c) shows the values for each cycle using the same sensor. Here the first thing to notice is that the change in resistance \(\frac{\Delta R}{R_0}\) exhibited negative values during the first cycle. In this first cycle, the MWCNT’s were disposed of/aligned according to the applied load direction. Thus, the subsequent cycles exhibited an increasing \(\frac{\Delta R}{R_0}\) behavior. We have to point out that this behavior was linear until an elongation ratio ranged between 1.2-1.25. Beyond this range the slope of the \(\frac{\Delta R}{R_0}\) vs. elongation ratio curves decreased. This is an interesting finding because the slope of the curves \(\frac{\Delta R}{R_0}\) vs. elongation ratio is, in fact, the gage factor (GF) of the strain sensor. In view of this, the initial (with \(\lambda \) between 1 and 1.25) and final (with \(\lambda \) between 1.25 and 1.42) slopes of the average \(\langle \frac{\Delta R}{R_0}\rangle \) (discarding cycle 1) was computed for each sensor; the averages are shown in Fig. 3 d), while the values of the slopes, or gage factors, are shown in Fig. 4 a-b) after running a linear fitting. Here, the gage factor average for the initial slope was 0.34 ±0.09 while the final slope reduced its value 4.25 times, offering an average Gage factor equal to 0.08 ±0.05. The corresponding reduction will be explained below when we discuss the simulations and present some basic theory of the phenomena involved.

Mechanical and electrical response under cyclic uniaxial tensile load

In this section, the mechanical and electrical response of PDMS-MWCNT’s resistive strain sensors under uniaxial load and unload cycling is presented. Figure 5 shows two double axes charts that relate the stress and \(\frac{\Delta R}{R_0}\) as a function of the elongation ratio during mechanical cycling. In this case, Fig. 5 a) presents the cycle 1 (initial cycle) where the mechanical response of PDMS presents a hysteretic mechanical behavior; however, after the complete unloading process, the stress value returned to zero. Regarding the electrical variable, we noticed for this first cycle that the values presented a negative slope for \(\frac{\Delta R}{R_0}\), and its initial value was not recovered. Nonetheless, the negative trend for \(\frac{\Delta R}{R_0}\) became positive for cycle 2 and beyond. Thus, we observed that the \(\frac{\Delta R}{R_0}\) value increased as the stress and elongation ratio also increased, as shown in Fig. 5 b). In the case of the electrical response (\(\frac{\Delta R}{R_0}\)) of the strain sensor we observe that this kind of sensors presented an hysteretic loop with a fish-shape; here the final value of \(\frac{\Delta R}{R_0}\) at the end of the unloading process was different to the initial one. At this point, comparing the Figs. 5 a) and b), we assumed that MWCNT’s experienced a physical alignment due to the applied load direction, which could explain the change of behavior of the \(\frac{\Delta R}{R_0}\) curves after the first cycle and beyond.

Fig. 6
figure 6

Electrical behavior of the PDMS-MWCNT’s resistive strain sensors: Sample 4, a) Electrical resistance behavior as a function of elongation ratio during 10 cycles of uniaxial tension. b) Maximum resistance value at the maximum load value for each cycle, c) \(\frac{\Delta R}{R_0}\) behavior as a function of elongation ratio during 10 cycles. d) Maximum \(\frac{\Delta R}{R_0}\) value at the maximum load value for each cycle

Full size image

To get a better comprehension of these results, first, we have to clarify the physics behind these experiments taking into account the following points: (1) A PDMS uniaxial tensile sample, with a dogbone shape, is been deformed. The tensile sample has embedded an MWCNT’s resistive circuit in an S-gage pattern; both conform to what we have labeled as flexible PDMS-MWCNT’s resistive strain gage sensor. (2) Applying a uniaxial tensile force to the flexible sensor, the polymeric matrix based on PDMS will be deformed, presenting a non-linear -but predictable- mechanical response obeying a first-order Ogden model. (3) The MWNCT’s forming the resistive strain gage S-pattern will also suffer the transmitted deformation through the PDMS polymeric matrix. Here we have to remember that the MWCNT’s strain gage S-Pattern was deposited by using a spraying technique and adhesive masks on a PDMS surface and subsequently encapsulated with another layer of PDMS. Therefore, the MWCNT’s were confined within the polymeric matrix but they will have a certain freedom of mobility in a range defined by their geometry (average diameter and length). (4) Thus, when the sensor is uniaxially loaded, the PDMS polymeric matrix will elongate in its longitudinal direction and will contract in perpendicular directions to the longitudinal one, due to its Poisson ratio effect. (5) The current imposed stress-elongation ratio condition to the flexible PDMS matrix would be transmitted to the MWCNT’s strain gage S-Pattern; furthermore, the MWCNT’s strain gage S-Pattern would have to be deformed in the same sense, provoking a diminution of the MWCNT’s S-pattern cross-section area and therefore an increase of electrical resistance value.

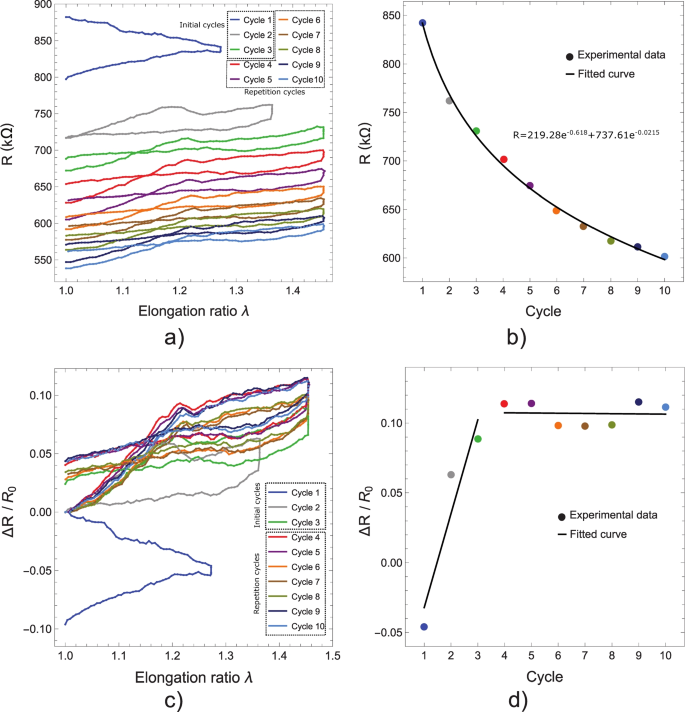
Considering these 5 points, the results presented in Fig. 6 can be explained clearly. Figure 6 a) shows a representative resistance behavior as a function of the elongation ratio of the PDMS-MWCNT’s resistance strain sensors. As it was mentioned before, we realized for the first cycle that the values presented a negative slope for electrical resistance (R), and its initial value was not recovered. Nonetheless, the negative trend for R and \(\frac{\Delta R}{R_0}\) became positive for cycle 2 and beyond, as shown in Figs. 6 a) and c). This kind of behavior was observed on cycle 2 and beyond for elongation ratios ranging between 1 and 1.25, which upon increasing the elongation ratio, an increase in resistivity was produced; however, for elongation ratios larger than 1.25 we observed that this increasing behavior suffered a change (a decrement) in its slope, as reported before in the gage factor charts (see Figs. 4 a and b). It means that the values of R and therefore \(\frac{\Delta R}{R_0}\) tend to decrease at higher elongation ratios. This behavior, a priori, is contradictory to the first stage of elongation (\(\lambda \)=1-1.25); however, these results are consistent if the changes of alignment/interaction and distance between MWCNT’s are considered in the resistive response. In simple words, the flexible PDMS-MWCNT’s resistive strain gage sensor becomes more conductive for larger elongation ratios than 1.25 due to the effect of the Poisson ratio and the interaction between MWCNT’s. In these terms, we postulate that for elongation ratios higher than 1.25, the nanotubes get aligned in the direction of the application of the load; besides, the distance between them gets shorter compared to what they had in the initial loading stage. Therefore, the conjunction of these two factors will decrease the path/distance that the electrons have to travel, giving rise to the tunnel effect in the MWCNT’s neighborhood and, thus, improving the conductivity of the MWCNT’s strain gage S-Pattern and therefore decreasing the parameter \(\frac{\Delta R}{R_0}\) for \(1.25>\lambda \). So far, the only way to support these arguments is our own results and the numerical simulations that will be presented later. For now, a more detailed analysis of the behavior of the electrical resistance values (R) and the \(\frac{\Delta R}{R_0}\) values of the sensors under a greater number of cycles is presented.

Figure 6 a) shows that from cycle to cycle the electrical resistance clearly decrease. Thus, if we select the maximum value of the electrical resistance from these curves as a function of the number of cycles, an exponential decay curve is obtained as shown in Fig. 6 b); Nonetheless, if we select the same point on the elongation/resistance curves (see Fig. 6 c) but now considering the ratio \(\frac{\Delta R}{R_0}\), we obtained a constant value for those maximum \(\frac{\Delta R}{R_0}\) values after a certain number of cycles, as shown Fig. 6 d). Notice that the first two points (cycles 1 and 2) correspond to lower elongation ratios; therefore, they did not reach a value close to 0.1 as the others. Our results suggest that PDMS-MWCNT’s resistive strain sensors can be trained after a certain number of mechanical load-unload cycles to improve the repeatability of the flexible strain sensors’ signal, and that it is the ratio \(\frac{\Delta R}{R_0}\) the parameter that reaches a stationary value. Thus, in order to probe it, we carried out another 20 cycles more, as shown in Fig. 7.

Fig. 7
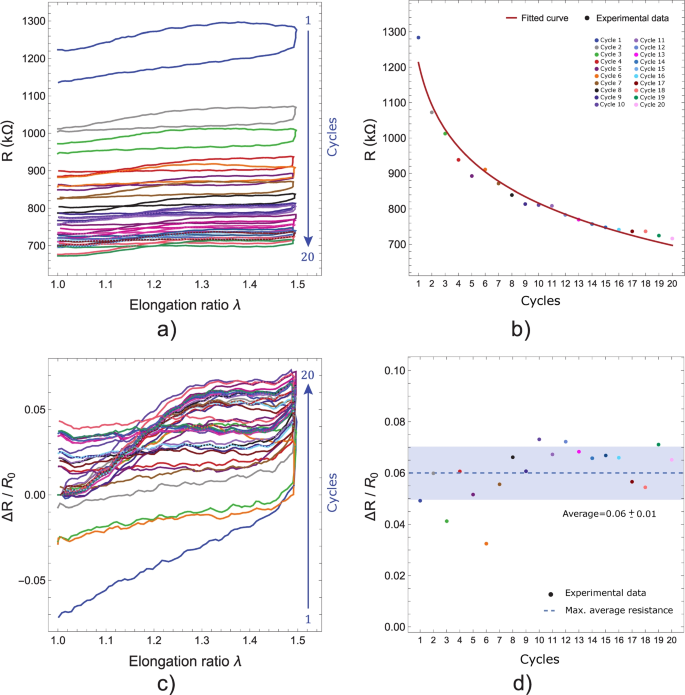
figure 7

Extension of mechanical cycling over 20 more loading and unloading cycles. a) Electrical resistance response as a function of elongation ratio during 20 extra cycles. b) Maximum resistance value at the maximum load value for each cycle, c) \(\frac{\Delta R}{R_0}\) behavior as a function of elongation ratio during 10 cycles. d) Maximum values of \(\frac{\Delta R}{R_0}\) for each cycle

Full size image

In this case, the load-unload cumulative cycles were registered and plotted. Figure 7 a) depicts the electrical resistance as a function of elongation ratio curves for 20 cycles more (10 cycles presented in Fig. 6 a) and other 20 cycles presented in 7 a) summing a total of 30 cycles. Here we can observe that the initial cycles of Figs.6 a) and 7 a) presented differences between the R vs \(\lambda \) loops; however, after a couple of cycles, these loops tend to present similar shapes between them and it was observed a decrease of the electrical resistance values which remained stuck between 680 and 720 k\(\Omega \). Now, considering again the maximum value of the electrical resistance during the loading process, the chart shown in Fig. 7 b) was obtained. Here, it is observed that the maximum electrical resistance values again showed an exponential decay curve. Subsequently, we performed the calculation to obtain the \(\frac{\Delta R}{R_0}\) as function of elongation ratio curves, obtaining the fish shape curves for the vast majority of the cycles except for the first three cycles, see Fig. 7 c). Thus, when the maximum values of \(\frac{\Delta R}{R_0}\) as function of cycles were plotted in 7 d) a trend was observed reaching a \(\frac{\Delta R}{R_0}\) average value of 0.06 ±0.01. This demonstrates consistency between these electrical resistance measurements as a function of the elongation ratio, positioning PDMS-MWCNT’s composites as promising resistive strain sensors. We still have to understand the change of gage factor which is associated to the slope change of the \(\frac{\Delta R}{R_0}\) vs. elongation ratio curves. Hence, numerical simulations were conducted together with some theoretical considerations.

Fig. 8
figure 8

Numerical version of the flexible strain sensor based on PDMS and MWCNT’s, a) unstrained configuration b) strained configuration, c) Scheme of two nanotubes pointing in directions \({\textbf {u}}\), \({\textbf {u'}}\) and having a distance d. The director \({\textbf {n}}\) points to the principal strain direction, d) Stress as a function of the elongation ratio; (\(\circ \)) experiments, (-) Ogden’s model, (- -) Mooney-Rivlin’s model. Bulk modulus K = 962 MPa, best fittings for Ogden’s model: \(\mu _1\) = 0.362 MPa, \(\alpha _1\) = 1.32106, for Mooney-Rivlin: C\(_{10}\) = 0.2408 MPa, C\(_{01}\) = -0.0437 MPa and e) Relative resistance change as a function of elongation ratio: (\(\circ \)) experiments, dashed line: Eq. 7, solid line: Eq. 8 with \(d_{0}\)=0.1nm, dotted line: Eq. 8 with \(d_{0}\)=0.2nm

Full size image

Numerical simulations and theoretical considerations

As an example of the deformation states obtained numerically, Fig. 8 a-b) shows the deformation of the numerical simulated sensor before and after applying an elongation ratio of \(\lambda \)=1.27. Figure 8 d) shows a representative experimental (circles) uniaxial stress progression as shown by the z-stress plot as a function of the elongation ratio and the corresponding comparison with the simulations (lines). It is important to say that since in the numerical simulations we obtained the full stress field inside and on the boundaries of the sensor, an average procedure has to be done in order to compare the numerical values with the single stretch stress value (nominal stress) given by the mechanical transducer in the experiments. In this sense, we noticed that the maximum stress obtained numerically on the axial faces had a better match. It turns out that the z-stress obtained with Ogden’s model (solid line in Fig. 8 d) had a very good match with the experimental data, but not so if we use another model such as the Mooney-Rivlin model (dashed line), which is also a popular model for hiperelasticity. This is a surprise given that both models can be fitted correctly to the same experimental data since the beginning. According to the existing literature, this apparent drawback of Mooney-Rivlin’s model has to do with the available experimental dataset used to find the model’s parameters rather than with the model itself. It has been shown that if one uses several datasets of strain progression to fit the model’s parameters, the performance of the model is substantially better (i.e., use uniaxial, biaxial, planar, bulge test, etc., rather than just one of these) [25, 26]. Ogden´s model matched the experimental data using just a uniaxial dataset to estimate its parameters can be seen as an advantage in favor to this model, after all, it has also been shown that it exhibits lower residuals in the fittings and can be applied to a wider range of strains compared to Mooney-Rivlin [27]. The insets of Fig. 8 d) show in more detail the differences between both models, revealing that Mooney-Rivlin tends to overestimate the stress in the neck region of the sensor. In any case, we insist that Mooney-Rivlin could be improved if other data sets were used in the fitting procedure rather than just uniaxial strain.

Now, to establish a clear distinction between the macroscopic/microscopic effects on the observed changes of the electrical resistance in the sensors, let’s start our analysis by assuming that the microstructure of the nanotubes does not changes at all with the strain \(\varepsilon \). This means that any change we detect in the electrical resistance R as a function of \(\varepsilon \) will be of ohmic consequence, that is, will be a result of having longer conductive paths as strain increases, while having lower transversal number of paths due to transversal contraction or Poisson ratio \(\nu \). These geometrical effects are captured by Eq. 7,

$$\begin{aligned} \frac{\Delta {R}}{R_{o}}=\frac{l(\varepsilon )}{l_{o}}\frac{A_{o}}{A(\varepsilon )}-1\approx (1+\varepsilon )^{1+2\nu }-1 \end{aligned}$$
(7)

where \(l(\varepsilon )\), \(l_{o}\) are the length and initial length of the MWCNT path and \(A(\varepsilon )\) and \(A_{o}\) are the transverse area and initial transverse area of the path, respectively. Equation 7 is plotted in Fig. 8 e) (dashed line) and was calculated using \(l(\varepsilon )\) and \(A(\varepsilon )\) as determined from the numerical simulations (assuming that the thickness of the MWCNT path, \(\sim 1\mu {m}\), is kept constant). The second equivalence in Eq. 7 was corroborated (\(\nu \sim 0.5\) for PDMS) and gives the same straight dashed line in Fig. 8 e). We can immediately observe that ohm’s law gives a much higher electric resistance than that observed in the experiments; in other words, the changes in the microstructure that should be occurring as \(\varepsilon \) increases must facilitate, rather than hinder, the conductive process. This is perhaps in contradiction to the general paradigm that states that strain hinders conduction and disrupts the conductive paths. Again, we insist here that the difference observed in our system is due to the fact that the MWCNT arrays form a highly concentrated path with almost negligible free volume. Therefore, in view that ohm’s law is not sufficient to explain the experimental curve, we must accept that the intrinsic resistivity \(\rho \) of the MWCNT path is also changing, that is,

$$\begin{aligned} \frac{\Delta {R}}{R_{o}}=\frac{\rho (\varepsilon )}{\rho _{o}}(1+\varepsilon )^{1+2\nu }-1 \end{aligned}$$
(8)

or that \(\rho (\varepsilon )/\rho _{o}\ne 1\). We noticed that \(\rho (\varepsilon )/\rho _{o}\) should have an empirical form of

$$\begin{aligned} \frac{\rho (\varepsilon )}{\rho _{o}}=1+C_{1}\varepsilon +C_{2}\varepsilon ^{2} \end{aligned}$$
(9)

to fit a typical experimental curve, see the solid line in Fig. 8 e) for \(C_{1}=-1.49\), \(C_{2}=1.19\). What we should do now is try to obtain Eq. 9 using some first principles. As a simplistic but representative model, let us consider a pair-based interaction model or just two nanotubes (pairwise interactions) pointing in directions \({\textbf {u}}\), \({\textbf {u'}}\) as shown in Fig. 8 c). The director \({\textbf {n}}\) is also shown and represents, for example, the direction of the principal (local) strain. At this pair interaction point of view, we can assume that the critical resistivity came from tunnel effects such as [28, 29]

$$\begin{aligned} \rho (\epsilon )=\frac{d(\epsilon )}{\mathcal {A}(\epsilon )}\frac{h^{2}}{e^{2}\sqrt{2m\Psi }}\; exp\left( \frac{4\pi \sqrt{2m\Psi }}{h}d(\epsilon ) \right) \end{aligned}$$
(10)

where \(h=6.626\times 10^{-34}J\cdot {s}\) is Planck’s constant, e and m are the charge and mass (\(9.109\times 10^{-31}kg\)) of the electron, \(\Psi \) is the work function and \(\mathcal {A}(\epsilon )\), \(d(\epsilon )\) are the overlapping area and centroid-to-centroid distance between two nanotubes, respectively. Similar to other works [30, 31], we are going to define the inter-tube distance as

$$\begin{aligned} d(\epsilon )\simeq d_{o}(1-\nu \epsilon ) \end{aligned}$$
(11)

for some initial distance \(d_{o}\) and Poisson lateral contraction. With this, we are indeed assuming that a high population of nanotubes accommodates as suggested in Fig. 8 c) for small strains. Now, for symmetric nanotubes, the overlapping area should be an even function of the dot product \({\textbf {u}}\cdot {\textbf {u'}}\), that is, \(\mathcal {A}\sim {LD}({\textbf {u}}\cdot {\textbf {u'}})^{2}\), where L and D are the length and diameter of the nanotubes. At this point is convenient to recap the definition of the order parameter \(\mathcal {S}\) and which is commonly used in the theory of liquid crystals. \(\mathcal {S}\) is defined as: [23]

$$\begin{aligned} \mathcal {S}=\frac{3}{2}\langle ({\textbf {u}}\cdot {\textbf {n}})^{2}-\frac{1}{3} \rangle \end{aligned}$$
(12)

such that \(\mathcal {S}=0\) (\(({\textbf {u}}\cdot {\textbf {n}})^{2}=1/3\)) for an isotropic phase, while \(\mathcal {S}=1\) (\(({\textbf {u}}\cdot {\textbf {n}})^{2}=1\)) for a perfect nematic phase. Here \(\langle ...\rangle \) indicates some orientational average over the ensemble. In view of Eq. 12, it is convenient to approximate the area \(\mathcal {A}\) as

$$\begin{aligned} \mathcal {A}=\Delta \mathcal {A}+\mathcal {A}_{o}\simeq \frac{2}{3}LD\mathcal {S}+\mathcal {A}_{o} \end{aligned}$$
(13)
Fig. 9
figure 9

Flexible strain sensor based on PDMS and MWCNT’s used to measure the wrist extension of a male subject, a) Image of the instrumented sensor attached on the skin b) Acquired signal registering the changes of resistance during the human wrist extension movement

Full size image

where we have assumed that \(\langle ({\textbf {u}}\cdot {\textbf {n}})^{2}\rangle \sim \langle ({\textbf {u}}\cdot {\textbf {u'}})^{2}\rangle \) and \(\mathcal {A}_{o}\sim {LD}/3\). By doing this we are directly relating the overlapping area with the order parameter. Now, we need to propose a state equation for \(\mathcal {S}=\mathcal {S}(\epsilon )\). In principle, the change of \(\mathcal {S}\) as a function of \(\epsilon \) may be a complicated function of the mechanical parameters (bending, stretching) of the nanotubes, its concentration, aspect ratio, as well as nonlinear or collective effects such as entanglement or clusterization of the nanotubes as they align towards \({\textbf {n}}\). To keep things simple, we are going to use the fact that non-equilibrium molecular dynamics simulations [32, 33] made of an ensemble of linear polymer melts show that the order parameter displays a saturation curve with respect to the strain. Therefore, it seems plausible to propose a general expression of the form

$$\begin{aligned} \mathcal {S}=\frac{S_{max}\epsilon }{k+\epsilon } \end{aligned}$$
(14)

which represents a typical saturation behavior. Upon substituting Eqs. 11, 13 and 14 into Eq. 10, we can estimate the resistivity ratio as

$$\begin{aligned} \frac{\rho (\epsilon )}{\rho _{o}}=(1-\nu {\epsilon })\left( 1+\frac{2\mathcal {S}_{max}\epsilon }{k+\epsilon } \right) ^{-1}\;exp(-\zeta \nu {d_{o}}\epsilon ) \end{aligned}$$
(15)

where \(\zeta =4\pi \sqrt{2m\Psi }/h\). Upon Taylor expanding Eq. 15 up to \(\mathcal {O}(\epsilon )^{2}\) we get, precisely, the polynomial form of Eq. 9 with coefficients defined as:

$$\begin{aligned} C_{1}= & -\left( \zeta {d}_{o}\nu +\frac{2\mathcal {S}_{max}}{k}+\nu \right) \nonumber \\ C_{2}\!=\! & \frac{2\mathcal {S}_{max}}{k}\left( \frac{1}{k}\!+\!\frac{2\mathcal {S}_{max}}{k}\!+\!\nu (1\!+\!\zeta {d}_{o}) \right) \!+\!\zeta {d}_{o}\nu (\nu \!+\!\zeta {d}_{o}\nu /2) \end{aligned}$$
(16)

The theoretical black line in Fig. 8 e) is reproduced for the following choice of parameters: \(\Psi =4.6eV\), \(d_{o}\sim 0.1nm\), \(k=3.7\), \(\nu =0.34\), \(\mathcal {S}_{max}=0.54\). First of all, it was fortunate that with so few theoretical assumptions, we could obtain the correct form capable of reproducing the experimental results closely. This indicates that the rearrangements of the nanotubes are indeed changing the intrinsic conductivity in a way that favors electron tunneling, and the way this happens is by sustaining a continuous decrease of the inter-nanotube distance with the strain while increasing the overlapping area. Moreover, the selection of parameters is close to the values they are supposed to have: \(\Psi =4.6eV\) is a typical value of the work function for CNT [34], while a distance of \(d_{o}\sim 0.1nm\) is also of the order of the electron hopping distance (the MWCNT network we have is additionally highly concentrated). Standout the fact that for the best fit, the Poisson ratio \(\nu \sim 0.34\) is closer to pristine MWCNT than to PDMS. This agrees with the fact that the MWCNT thin layer is composed mainly of nanotubes since they were not blended with uncured PDMS. Finally, the value of \(\mathcal {S}_{max}\sim 0.54\) suggests that the nanotube carpet is far from rearranging into a crystalline ordered phase upon application of the strain. Now, a question arises if our model can predict negative values of \(\Delta {R}/R_{o}\) as those observed in the first stretching cycles practiced on the experimental sensors. As shown in Fig. 8 e), dotted line, leaving all values fixed except that now \(d_{o}=0.2nm\) (indeed a small change in the inter-tube distance) Eqs. 8, 9 and 16 yield negative values of \(\Delta {R}/R_{o}\) and a negative slope up to \(\lambda =1+\epsilon \sim 1.25\). At first sight, it seems contradictory to obtain better conduction (negative values of resistance) for higher values of the inter-tube distance. However, remember that we are calculating the relative change of R, \(\Delta {R}/R_{o}\), so in the limit \(d_{o}\rightarrow 0\) the nanotubes cannot longer accommodate as \(\epsilon \) increases and the intrinsic resistivity will be constant (indeed, in the limit \(d_{o}\rightarrow 0\), Eqs. 8, 9 and 16 tend to Eq. 7 or \(\rho (\epsilon )/\rho _{o}\approx 1)\). In view of this, it seems that the cycles of expansion conducted in the experiments led to an effect of compaction in which the nanotubes re-accommodate, having each time lower values of \(d_{o}\). In summary, our working equation, Eq. 8, is able to capture both the macroscopic geometrical ohmic changes and the micro/nanoscopic reorientations of the nanotubes in the total change of \(\Delta {R}/R_{o}\). The numerical simulations helped us to elucidate further the role specifically brought by the macroscopic geometrical changes and to establish a clear distinction between one and the other.

Biometric realization

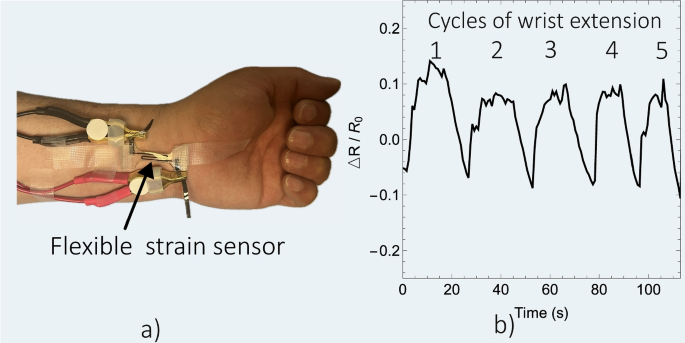
Once the flexible strain sensors were fully electrically and mechanically characterized, then they were used to measure the strain associated with a human wrist extension movement as shown in Fig. 9 a) and b). In this chart, the change in resistance associated with wrist extension during 5 cycles is observed. The average of maximum values of \(\frac{\Delta R}{R_0}\) was 0.09 \(\pm {0.02}\). It means that the flexible strain sensor was subjected to an elongation ratio close to 1.4 and suffered a normal stress close to 0.28 MPa during the cycles of wrist extension movement.

Conclusions

Low-cost, flexible strain sensors were obtained by spraying a conductive thin layer of MWCNT’s following an S-pattern embedded within the PMDS matrix exhibiting a dogbone-shaped tensile specimen, which was successfully used to measure the strain associated with a human wrist extension movement. Although significant work has been done in developing flexible strain sensors, ours is unique, as far as we know, in that it is based on standard geometry such as ASTM D1708 to minimize the effects on the mechanical behavior response of the sensor associated with its geometry. Our results demonstrated that the stress vs. elongation ratio and \(\frac{\Delta R}{R_0}\) vs. elongation ratio curves presented non-linear behaviors. In this sense, the non-linear electrical response of the sensor is composed of two well-defined linear regions, the first ranging between elongation ratios of 1 to 1.25 and the second one ranging from 1.25 to 1.4. Thus, we obtained gage factors of 0.34 ±0.09 and 0.08 ±0.05, respectively. According to the reported elongation ratios and considering the definition of engineering strain, these sensors can detect large strains up to 40% for several uniaxial loading-unloading cycles. The electrical response of the sensor (\(\frac{\Delta R}{R_0}\) vs. elongation ratio curves) shows fish-shape curves, which tended to present a steady behavior after ten cycles; it suggests that MWCNT’s contained in the conductive S-pattern tend to self-accommodate according to load magnitude and direction. This assumption was proved by the simulation results and theoretical assumptions considered in this work and allowed us to clearly distinguish the role between the macroscopic geometrical effects (ohmic effects) and micro/nanoscopic effects such as tunneling effect and change of the orientation of the nanotubes in terms of the applied strain. We think this distinction is an important contribution from the point of view of the understanding of polymer/nanoparticle materials and its electrical response to mechanical deformations. At this point, we conclude that our sensor works with a combination of mechanisms, such as piezoresistive and tunneling effects, which will depend on the level of the external solicitations applied to the sensor.