Орбита на Месечината
 Орбитата на Месечината е наклонета 5,14° кон еклиптиката. | |
| Голема полуоска | 384.748 км[1] |
|---|---|
| Средно растојание | 385.000 км[2] |
| Обратна синусна паралакса[б 1] | 384.400 км |
| Перигеј | 363.228,9 прос. (356400–370400 км) |
| Апогеј | 405.400 прос. (404000–406700 км) |
| Средна занесеност | 0,0549006 (0,026–0,077)[3] |
| Среден наклон | 6,687°[5] |
| Средна наваленост | |
| на орбитата кон еклиптиката | 5,15° (4,99–5,30)[3] |
| на месечевиот екватор кон еклиптиката | 1,543° |
| Период на | |
| орбитата околу Земјата (ѕвезден) | 27,322 дена |
| орбитата околу Земјата (средбен) | 29,530 дена |
| прецесија на јазлите | 18,5996 години |
| прецесија на апсидната линија | 8,8504 години |
Месечината кружи околу Земјата во напредна насока и завршува една револуција во однос на пролетната рамнодневица и ѕвездите за околу 27,32 дена (тропски месец и сидерален месец) и една револуција во однос на Сонцето за околу 29,53 дена ( синодиски месец ). Земјата и Месечината кружат околу нивното заедничко тежиште, кој се наоѓа околу 4,670 километри од центарот на Земјата (околу 73% од нејзиниот полупречник), сочинувајќи состав наречен систем Земја-Месечина. Во просек, растојанието до Месечината е околу 385.000 км од центарот на Земјата, што одговара на околу 60 Земјини полупречници или 1.282 светлосни секунди.
Со средна орбитална брзина од 1.022 км/с [6] Месечината поминува приближно растојание од својот пречник, или околу половина степен на небесната сфера, секој час. Месечината се разликува од повеќето сателити на другите планети по тоа што нејзината орбита е блиску до еклиптичката рамнина наместо до нејзината примарна (во овој случај, Земјината) екваторска рамнина. Орбиталната рамнина на Месечината е наклонета за околу 5,1° во однос на еклиптичката рамнина, додека екваторската рамнина на Месечината е навалена за само 1,5°.
Својства
[уреди | уреди извор]Својствата на орбитата опишани во овој дел се приближни. Орбитата на Месечината околу Земјата има многу варијации (растројувања) поради гравитациската привлечност на Сонцето и планетите, чие проучување (теоријата на Месечината) има долга историја.[7]
Елиптичен облик
[уреди | уреди извор]Орбитата на Месечината е речиси кружна елипса околу Земјата (полуглавните и полуминорните оски се 384.400 км и 383.800 км, соодветно: разлика од само 0,16%). На равенката на елипса дава ексцентричност на 0,0549 и перигеј и апогеј растојанија од 362.600 км и 405.400 км соодветно (разлика од 12%).
Бидејќи поблиските објекти изгледаат поголеми, привидната големина на Месечината се менува додека се движи кон и подалеку од набљудувачот на Земјата. Настанот познат како „супермесечина“ се случува кога полната Месечина е најблиску до Земјата (перигеј). Најголемиот можен привиден пречник на Месечината е исто 12% поголем (како перигеј наспроти апогејски растојанија) од најмалиот; привидната површина е 25% повеќе, а исто така е и количината на светлина што ја рефлектира кон Земјата.
Варијансата во орбиталното растојание на Месечината кореспондира со промените во нејзината тангенцијална и аголна брзина, како што е наведено во вториот Кеплеровиот закон . Просечното аголно движење во однос на замислен набљудувач во тежиштето Земја-Месечина е 13,176 ° на ден на исток ( J2000,0 ).
Издолжување
[уреди | уреди извор]Издолжувањето на Месечината е нејзиното аголно растојание источно од Сонцето во секое време. На млада месечина, таа е нула и се вели дека Месечината е во сврзување. При полна месечина, издолжувањето е 180° и се вели дека е во противположба. Во двата случаи, Месечината е во сизигија, односно Сонцето, Месечината и Земјата се речиси подредени. Кога издолжувањето е или 90° или 270°, се вели дека Месечината е во квадратура.
Прецесија
[уреди | уреди извор]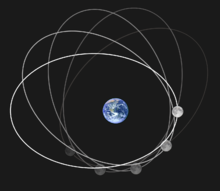

Ориентацијата на орбитата не е фиксирана во просторот, туку ротира со текот на времето. Оваа орбитална прецесија се нарекува апсидна прецесија и е ротација на орбитата на Месечината во рамките на орбиталната рамнина, односно оските на елипсата ја менуваат насоката. Главната оска на месечевата орбита - најдолгиот пречник на орбитата, спојувајќи ги нејзините најблиски и најоддалечени точки, перигејот и апогејот, соодветно - прави една целосна револуција на секои 8,85 Земјини години, или 3.232,6054 дена, додека ротира бавно во иста насока како самата месечина (директно движење) - што значи прецесира кон исток за 360°. Апсидната прецесија на Месечината се разликува од јазолната прецесија на нејзината орбитална рамнина и осната прецесија на самата Месечина.
Наклонетост
[уреди | уреди извор]Просечниот наклон на орбитата на Месечината кон еклиптичката рамнина е 5,145°. Теоретските размислувања покажуваат дека сегашната наклонетост во однос на еклиптичката рамнина настанала со плимна еволуција од претходна орбита близу Земјата со прилично постојан наклон во однос на екваторот на Земјата.[8] Потребно е наклонетост на оваа претходна орбита од околу 10° кон екваторот за да се добие сегашен наклон од 5° кон еклиптиката. Се смета дека првично наклонот кон екваторот бил близу нула, но можел да се зголеми на 10° преку влијанието на планезималите кои минувале во близина на Месечината додека паѓале на Земјата.[9] Да не се случело ова, Месечината сега ќе лежела многу поблиску до еклиптиката, а затемнувањата ќе биле многу почести.[10]
Вртежната оска на Месечината не е нормална на нејзината орбитална рамнина, па месечевиот екватор не е во рамнината на нејзината орбита, туку е наклонет кон неа за константна вредност од 6,688° (косината). Како што било откриено од Жак Касини во 1722 година, вртежната оска на Месечината се прецеси со иста брзина како и нејзината орбитална рамнина, но е 180° надвор од фаза. Според тоа, аголот помеѓу еклиптиката и месечевиот екватор е секогаш 1,543°, иако вртежната оска на Месечината не е фиксирана во однос на ѕвездите.[11]
Јазли
[уреди | уреди извор]Јазлите се точки во кои орбитата на Месечината ја преминува еклиптиката. Месечината го преминува истиот јазол на секои 27,2122 дена, интервал наречен драконски месец. Линијата на јазли, пресекот помеѓу двете соодветни рамнини, има повратно движење: за набљудувач на Земјата, таа ротира на запад по еклиптиката со период од 18,6 години или 19,3549° годишно. Кога се гледаат од небесниот север, јазлите се движат во насока на стрелките на часовникот околу Земјата, спротивно на вртењето на Земјата и нејзината револуција околу Сонцето. Затемнување на Месечината или Сонцето може да се случи кога јазлите се усогласуваат со Сонцето, приближно на секои 173,3 дена. Наклонот на орбитата на Месечината, исто така, ги одредува затемнувањата; сенките се вкрстуваат кога јазлите се совпаѓаат со полна и млада месечина кога Сонцето, Земјата и Месечината се порамнуваат во три димензии.
Всушност, тоа значи дека „тропската година“ на Месечината е долга само 347 дена. Ова се нарекува драконска година или година на затемнување. Во овој период се вклопуваат „сезоните“ на Месечината. Околу половина од оваа драконска година, Сонцето е северно од месечевиот екватор (но најмногу 1,543°), а во другата половина е јужно од месечевиот екватор. Очигледно, ефектот на овие сезони е помал во споредба со разликата помеѓу месечевата ноќ и месечевиот ден. На месечевите полови, наместо вообичаените месечеви денови и ноќи од околу 15 Земјини денови, Сонцето ќе биде „горе“ 173 дена како што ќе биде „долу“; Поларното изгрејсонце и зајдисонце трае 18 дена секоја година. „Горе“ овде значи дека центарот на Сонцето е над хоризонтот.[12] Месечевите поларни изгрејсонца и зајдисонца се случуваат околу времето на затемнувањето (сончево или месечево). На пример, при затемнувањето на Сонцето на 9 март 2016 година, Месечината била во близина на нејзиниот јазол што опаѓа, а Сонцето било блиску до точката на небото каде што екваторот на Месечината ја преминува еклиптиката. Кога Сонцето ќе ја достигне таа точка, центарот на Сонцето заоѓа на месечевиот северен пол и изгрева на месечевиот јужен пол.
Затемнувањето на Сонцето на 1 септември истата година, Месечината била во близина на нејзиниот растечки јазол, а Сонцето било блиску до точката на небото каде што екваторот на Месечината ја преминува еклиптиката. Кога Сонцето ќе ја достигне таа точка, центарот на Сонцето изгрева на месечевиот северен пол и заоѓа на месечевиот јужен пол.
Наклон кон екваторот и застој на Месечината
[уреди | уреди извор]На секои 18,6 години, аголот помеѓу орбитата на Месечината и екваторот на Земјата достигнува максимум 28°36′, збирот на екваторското навалување на Земјата (23°27′) и орбиталниот наклон на Месечината (5°09′) кон еклиптиката. Ова се нарекува голем месечев застој. Отприлика во ова време, деклинацијата на Месечината ќе варира од -28°36′ до +28°36′. Спротивно на тоа, 9,3 години подоцна, аголот помеѓу орбитата на Месечината и екваторот на Земјата го достигнува својот минимум од 18°20′. Ова се нарекува мал застој на Месечината. Последниот застој на Месечината имал мал застој во октомври 2015 година. Во тоа време опаѓачкиот јазол бил порамнет со рамнодневицата (точката на небото има нулта десно искачување и деклинација). Јазлите се движат кон запад за околу 19° годишно. Сонцето преминува даден јазол околу 20 дена порано секоја година.
Кога наклонот на орбитата на Месечината кон екваторот на Земјата е на минимум 18°20′, центарот на дискот на Месечината ќе биде над хоризонтот секој ден од географски широчини помали од 70°43' (90° - 18°20' – 57' паралакса) север или југ. Кога наклонот е максимум од 28°36', центарот на дискот на Месечината ќе биде над хоризонтот секој ден само од географски широчини помали од 60°27' (90° − 28°36' – 57' паралакса) на север или југ.
На повисоки географски широчини, ќе има период од најмалку еден ден секој месец кога Месечината не изгрева, но исто така ќе има период од најмалку еден ден секој месец кога Месечината не заоѓа. Ова е слично на сезонското однесување на Сонцето, но со период од 27,2 дена наместо 365 дена. Забележливо е дека точка на Месечината всушност може да биде видлива кога е околу 34 лачни минути под хоризонтот, поради атмосферско прекршување.
Поради наклонетоста на орбитата на Месечината во однос на екваторот на Земјата, Месечината е над хоризонтот на Северниот и Јужниот пол речиси две недели секој месец, иако Сонцето е под хоризонтот шест месеци одеднаш. Периодот од изгрејсонце до изгрејсонце на половите е тропски месец, околу 27,3 дена, доста блиску до сидералниот период. Кога Сонцето е најдалеку под хоризонтот (зимска краткодневица), Месечината ќе биде полна кога ќе биде на највисоката точка. Кога Месечината е во Близнаци, таа ќе биде над хоризонтот на Северниот Пол, а кога е во Стрелец ќе биде горе на Јужниот пол.
Светлината на Месечината се користи од зоопланктонот на Арктикот кога Сонцето е под хоризонтот со месеци [13] и мора да им помагала на животните кои живееле во регионите на Арктикот и Антарктикот кога климата била потопла.
Модел на скала
[уреди | уреди извор]-
Модел на скала на системот Земја-Месечина: Големините и растојанијата се во азмер. Го претставува средното растојание на орбитата и средните полупречници на двете тела.
Историја на набљудувања и мерења
[уреди | уреди извор]
Околу 1000 п.н.е., Вавилонците биле првата човечка цивилизација за која е познато дека водела постојана евиденција за набљудувањата на Месечината. Глинени плочи од тој период, кои се пронајдени на територијата на денешен Ирак, се испишани со клинесто писмо на кое се запишуваат времињата и датумите на изгрејсонцето и зајдисонцето, ѕвездите по кои Месечината поминала во близина и временските разлики помеѓу изгревањето и заоѓањето и на Сонцето и на Месечината околу времето на полна месечина. Вавилонската астрономија ги открила трите главни периоди на движењето на Месечината и користела анализа на податоци за да изгради месечеви календари кои се протегале во иднина.[7] Оваа употреба на детални, систематски набљудувања за да се направат предвидувања врз основа на експериментални податоци може да се класифицира како прва научна студија во историјата на човештвото. Сепак, се смета дека на Вавилонците им недостасувало геометриско или физичко толкување на нивните податоци и не можеле да ги предвидат идните затемнувања на Месечината (иако „предупредувањата“ биле издадени пред веројатните времиња на затемнување).
Старогрчките астрономи биле првите кои вовеле и анализирале математички модели на движење на предметите на небото. Птоломеј го опишал движењето на Месечината користејќи добро дефиниран геометриски модел на епицикли и евакција.[7]
Исак Њутн бил првиот што развил целосна теорија на движење. Набљудувањата на движењето на Месечината бил главниот тест на неговата теорија.[7]
Месечеви периоди
[уреди | уреди извор]| Име | Вредност (денови) | Дефиниција |
|---|---|---|
| Сидерален месец | 27,321662 | во однос на далечните ѕвезди (13,36874634 поминувања по сончева орбита) |
| Синодиски месец | 29,530589 | во однос на Сонцето (месечеви мени, 12,36874634 поминувања по сончева орбита) |
| Тропски месец | 27,321582 | во однос на пролетната точка (прецеси во ~ 26.000 години) |
| Аномалистички месец | 27,554550 | во однос на перигејот (прецеси во 3232.6054 дена = 8,850578 години) |
| Драконски месец | 27,212221 | во однос на растечкиот јазол (прецеси во 6793.4765 дена = 18,5996 години) |
Постојат неколку различни периоди поврзани со месечевата орбита.[14] Сидералниот месец е времето потребно за да се направи една целосна орбита околу Земјата во однос на неподвижните ѕвезди. Се работи за 27,32 дена. Синодискиот месец е времето кое и е потребно на Месечината да ја достигне истата визуелна фаза. Ова значително варира во текот на годината,[15] но во просек е околу 29,53 дена. Синодискиот период е подолг од сидералниот период затоа што системот Земја-Месечина се движи во својата орбита околу Сонцето во текот на секој сидерален месец, па затоа е потребен подолг период за да се постигне слично порамнување на Земјата, Сонцето и Месечината. Аномалистичкиот месец е времето помеѓу перигеите и е околу 27,55 дена. Одвојувањето Земја-Месечина ја одредува силата на месечевата плима што ја зголемува силата.
Драконскиот месец е времето од растечки јазол до растечки јазол. Времето помеѓу две последователни премини со иста еклиптичка должина се нарекува тропски месец. Последните периоди се малку поинакви од сидералниот месец.
Просечната должина на еден календарски месец (дванаесетина од годината) е околу 30,4 дена. Ова не е месечев период, иако календарскиот месец е историски поврзан со видливата месечева фаза.

Месечеви мени: 0 (1) - млада месечина, 0,25 - прва четвртина, 0,5 - полна месечина, 0,75 - последна четвртина
Плимна еволуција
[уреди | уреди извор]Гравитациската привлечност што Месечината ја врши на Земјата е причина за плимата и осеката и во океанот и во цврстата Земја; Сонцето има помало плимско влијание. Цврстата Земја реагира брзо на секоја промена во приливот, а изобличувањето добива облик на елипсоид со високите точки приближно под Месечината и на спротивната страна на Земјата. Ова е резултат на големата брзина на сеизмичките бранови во цврстата Земја.
Сепак, брзината на сеизмичките бранови не е бесконечна и, заедно со ефектот на загуба на енергија во рамките на Земјата, ова предизвикува мало доцнење помеѓу поминувањето на максималното присилување поради Месечината преку Месечината и максималната плима на Земјата. Бидејќи Земјата ротира побрзо отколку што Месечината патува околу нејзината орбита, овој мал агол произведува гравитациски вртежен момент што ја забавува Земјата и ја забрзува Месечината во нејзината орбита.
Во случајот со плимата и осеката, брзината на плимните бранови во океанот [16] е далеку побавна од брзината на присилувањето на Месечината. Како резултат на тоа, океанот никогаш не е во блиска рамнотежа со приливот. Наместо тоа, присилувањето генерира долги океански бранови кои се шират околу океанските басени додека на крајот не ја изгубат својата енергија преку турбуленции, или во длабоките океани или на плитки континентални полици.
Иако одговорот на океанот е покомплексен од двата, можно е да се подели плимата и осеката на океанот на мал елипсоиден термин кој влијае на Месечината плус втор член кој нема ефект. Елипсоидниот термин на океанот, исто така, ја успорува Земјата и ја забрзува Месечината, но бидејќи океанот троши толку многу плимна енергија, сегашните плими на океанот имаат поголем ефект од цврстата Земјина плима.
Поради плимниот вртежен момент, предизвикан од елипсоидите, дел од аголниот (или вртежен) импулс на Земјата постепено се пренесува на ротацијата на парот Земја-Месечина околу нивното заедничко тежиште.
Овој малку поголем орбитален аголен моментум предизвикува растојанието Земја-Месечина да се зголемува за приближно 38 милиметри годишно.[17] Зачувувањето на аголниот импулс значи дека осната ротација на Земјата постепено се забавува, и поради тоа нејзиниот ден се продолжува за приближно 24 микросекунди секоја година (со исклучок на глацијалното отскокнување). Двете бројки важат само за моменталната конфигурација на континентите. Плимните ритмити од пред 620 милиони години покажуваат дека, во текот на стотици милиони години, Месечината се повлекувала со просечна брзина од 22 милиметри годишно (2200 км или 0,56% или растојанието Земја-Месечина на сто милиони години) и денот се продолжува со просечна стапка од 12 микросекунди годишно (или 20 минути на сто милиони години),.
Сегашната висока стапка може да се должи на речиси резонанца помеѓу природните океански честоти и плимните честоти.[18] Друго објаснување е дека во минатото Земјата ротирала многу побрзо, ден кој веројатно траел само 9 часа на раната Земја. Добиените плимни бранови во океанот тогаш би биле многу пократки и би било потешко за приливите со долга бранова должина да ги возбудат плимата и осеката со кратка бранова должина.[19]
Месечината постепено се повлекува од Земјата во повисока орбита, а пресметките сугерираат дека тоа ќе продолжи околу 50 милијарди години.[20][21] Во тоа време, Земјата и Месечината би биле во меѓусебна резонанца на вртење-орбита или заклучување на плимата, во која Месечината ќе ја обиколи Земјата за околу 47 дена (моментално 27 дена), а и Месечината и Земјата ќе ротираат околу нивните оски во исто време, секогаш свртени еден кон друг со иста страна. Ова веќе и се случило на Месечината - истата страна секогаш е свртена кон Земјата - а исто така полека се случува и со Земјата. Сепак, забавувањето на ротацијата на Земјата не се случува доволно брзо за ротацијата да се продолжи до еден месец пред другите ефекти да ја променат ситуацијата: приближно 2,3 милијарди години од сега, зголемувањето на зрачењето на Сонцето ќе предизвика испарување на океаните на Земјата, отстранување на најголемиот дел од плимното триење и забрзување.
Либрација
[уреди | уреди извор]
Месечината е во синхрона ротација, што значи дека постојано го задржува истото лице кон Земјата. Оваа синхрона ротација е точно само во просек бидејќи орбитата на Месечината има дефинитивна ексцентричност. Како резултат на тоа, аголната брзина на Месечината варира додека кружи околу Земјата и затоа не е секогаш еднаква на брзината на ротација на Месечината која е поконстантна. Кога Месечината е на нејзиниот перигеј, нејзиното орбитално движење е побрзо од нејзината ротација. Во тоа време Месечината е малку понапред во својата орбита во однос на нејзината ротација околу својата оска, и тоа создава перспективен ефект кој овозможува да се види до осум степени на должина од нејзината источна (десна) далечна страна. Спротивно на тоа, кога Месечината ќе го достигне својот апогеј, нејзиното орбитално движење е побавно од нејзината ротација, откривајќи осум степени на должина од нејзината западна (лева) далечна страна. Ова е означено како оптичка либерација во должина.
Оската на вртење на Месечината е наклонета вкупно 6,7° во однос на нормалата на рамнината на еклиптиката. Ова води до сличен перспективен ефект во правец север-југ, кој се нарекува оптичка либрација во географска широчина, што овозможува да се видат речиси 7° од географската ширина надвор од полот на далечната страна. Конечно, бидејќи Месечината е оддалечена само околу 60 Земјини полупречници од центарот на масата на Земјата, набљудувач на екваторот кој ја набљудува Месечината во текот на ноќта се движи странично за еден пречник на Земјата. Ова доведува до дневна либрација, што овозможува да се види дополнителна должина од еден степен на Месечината. Од истата причина, набљудувачите на двата географски пола на Земјата би можеле да видат дополнителен степен на отчукување во географската ширина.
Покрај овие „оптички либрации“ предизвикани од промената на перспективата за набљудувач на Земјата, постојат и „физички либрации“ кои се вистински нутации на насоката на полот на ротација на Месечината во вселената: но тие се многу мали.
Патот на Земјата и Месечината околу Сонцето
[уреди | уреди извор]
Кога се гледа од северниот небесен пол (т.е. од приближниот правец на ѕвездата Северница), Месечината кружи околу Земјата спротивно од стрелките на часовникот, а Земјата околу Сонцето спротивно од стрелките на часовникот, а Месечината и Земјата ротираат на нивните оски спротивно од стрелките на часовникот.
Правилото за десната рака може да се користи за означување на насоката на аголната брзина. Ако палецот од десната рака покажува кон северниот небесен пол, неговите прсти се виткаат во правец во кој Месечината кружи околу Земјата, Земјата околу Сонцето, а Месечината и Земјата ротираат на нивните оски.
Во претставите на Сончевиот Систем, вообичаено е да се нацрта траекторијата на Земјата од гледна точка на Сонцето и траекторијата на Месечината од гледна точка на Земјата. Ова може да остави впечаток дека Месечината кружи околу Земјата на таков начин што понекогаш се враќа наназад кога се гледа од перспектива на Сонцето. Меѓутоа, бидејќи орбиталната брзина на Месечината околу Земјата (1 км/с) е мала во споредба со орбиталната брзина на Земјата околу Сонцето (30 км/с), ова никогаш не се случува.
Сметајќи го системот Земја-Месечина како двојна планета, нејзиниот центар на гравитација е во Земјата, околу 4,671 километри [23] или 73,3% од полупречникот на Земјата од центарот на Земјата. Овој центар на гравитација останува на линијата помеѓу центрите на Земјата и Месечината додека Земјата ја завршува својата дневна ротација. Патот на системот Земја-Месечина во неговата сончева орбита е дефиниран како движење на овој заеднички центар на гравитација околу Сонцето. Следствено, центарот на Земјата се врти внатре и надвор од сончевата орбитална патека во текот на секој синодичен месец додека Месечината се движи во својата орбита околу заедничкиот центар на гравитација.[24]
Гравитацискиот ефект на Сонцето врз Месечината е повеќе од двојно поголем од оној на Земјата на Месечината; следствено, траекторијата на Месечината е секогаш конвексна. Односно, областа опкружена со орбитата на Месечината кон Сонцето е конвексно множество.
Белешки
[уреди | уреди извор]- ↑ Обратната синусна паралакса ɑsin π традиционално е средното растојание на Месечината од Земјата (средиште до средиште), каде ɑ е Земјиниот екваторски полупречник, а π е Месечевата паралакса помеѓу краевите на ɑ.[3] Три од астрномските константи на IAU од 1976 г. биле „средно растојание од Месечината до Земјата“ 384.400 км, „екваторска хоризонтска паралакса при средно растојание" 3422,608″ и „екваторски полупречник на Земјата“ 6.378,14 км.[4]
Наводи
[уреди | уреди извор]- ↑ M. Chapront-Touzé; J. Chapront (1983). „The lunar ephemeris ELP-2000“. Astronomy & Astrophysics. 124: 54. Bibcode:1983A&A...124...50C.
- ↑ M. Chapront-Touzé; J. Chapront (1988). „ELP2000-85: a semi-analytical lunar ephemeris adequate for historical times“. Astronomy & Astrophysics. 190: 351. Bibcode:1988A&A...190..342C.
- ↑ 3,0 3,1 3,2 Meeus, Jean (1997), Mathematical Astronomy Morsels, Richmond, VA: Willmann-Bell, стр. 11–12, 22–23, ISBN 0-943396-51-4
- ↑ Seidelmann, P. Kenneth, уред. (1992), Explanatory Supplement to the Astronomical Almanac, University Science Books, стр. 696, 701, ISBN 0-935702-68-7
- ↑ Lang, Kenneth R. (2011), The Cambridge Guide to the Solar System, 2nd ed., Cambridge University Press.
- ↑ „Moon Fact Sheet“. NASA. Посетено на 2014-01-08.
- ↑ 7,0 7,1 7,2 7,3 Martin C. Gutzwiller (1998). „Moon-Earth-Sun: The oldest three-body problem“. Reviews of Modern Physics. 70 (2): 589–639. Bibcode:1998RvMP...70..589G. doi:10.1103/RevModPhys.70.589.
- ↑ Peter Goldreich (Nov 1966). „History of the Lunar Orbit“. Reviews of Geophysics. 4 (4): 411. Bibcode:1966RvGSP...4..411G. doi:10.1029/RG004i004p00411.
- ↑ Kaveh Pahlevan & Alessandro Morbidelli (Nov 26, 2015). „Collisionless encounters and the origin of the lunar inclination“. Nature. 527 (7579): 492–494. arXiv:1603.06515. Bibcode:2015Natur.527..492P. doi:10.1038/nature16137. PMID 26607544.
- ↑ Jacob Aron (Nov 28, 2015). „Flying gold knocked the moon off course and ruined eclipses“. New Scientist.
- ↑ „View of the Moon“. U. of Arkansas at Little Rock. Посетено на May 9, 2016.
- ↑ Calculated from arcsin(0.25°/1.543°)/90° times 173 days, since the angular radius of the Sun is about 0.25°.
- ↑ „Moonlight helps plankton escape predators during Arctic winters“. New Scientist. Jan 16, 2016.
- ↑ The periods are calculated from orbital elements, using the rate of change of quantities at the instant J2000.
- ↑ Jean Meeus, Astronomical Algorithms (Richmond, VA: Willmann-Bell, 1998) p 354.
- ↑ J.B. Zirkir (2013). The Science of Ocean Waves. Johns Hopkins University Press. стр. 264. ISBN 9781421410784.
- ↑ Williams, James G.; Boggs, Dale H. (2016). „Secular tidal changes in lunar orbit and Earth rotation“. Celestial Mechanics and Dynamical Astronomy (англиски). 126 (1): 89–129. Bibcode:2016CeMDA.126...89W. doi:10.1007/s10569-016-9702-3. ISSN 0923-2958.
- ↑ Williams, George E. (2000). „Geological constraints on the Precambrian history of Earth's rotation and the Moon's orbit“. Reviews of Geophysics. 38 (1): 37–60. Bibcode:2000RvGeo..38...37W. doi:10.1029/1999RG900016.
- ↑ Webb, David J. (1982). „Tides and the evolution of the Earth-Moon system“. Geophysical Journal of the Royal Astronomical Society. 70 (1): 261–271. Bibcode:1982GeoJ...70..261W. doi:10.1111/j.1365-246X.1982.tb06404.x.
- ↑ C.D. Murray; S.F. Dermott (1999). Solar System Dynamics. Cambridge University Press. стр. 184.
- ↑ Dickinson, Terence (1993). From the Big Bang to Planet X. Camden East, Ontario: Camden House. стр. 79–81. ISBN 0-921820-71-2.
- ↑ The reference by H. L. Vacher (2001) (details separately cited in this list) describes this as 'convex outward', whereas older references such as "The Moon's Orbit Around the Sun, Turner, A. B. Journal of the Royal Astronomical Society of Canada, Vol. 6, p. 117, 1912JRASC...6..117T"; and "H Godfray, Elementary Treatise on the Lunar Theory" describe the same geometry by the words concave to the sun.
- ↑ Seidelmann, P. Kenneth, уред. (1992), Explanatory Supplement to the Astronomical Almanac, University Science Books, стр. 701, ISBN 0-935702-68-7
- ↑ Aslaksen, Helmer (2010). „The Orbit of the Moon around the Sun is Convex!“. Посетено на 2006-04-21.
Надворешни врски
[уреди | уреди извор]- Поглед на Месечината Добри дијаграми на Месечината, Земјата, наклоните на орбитите и оските — Универзитетот на Арканзас
| ||||||||||



