Location via proxy:   [ UP ]  
[Report a bug]   [Manage cookies]                
Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2019 May 1.
Published in final edited form as: J Magn Reson. 2018 Mar 11;290:46–59. doi: 10.1016/j.jmr.2018.03.006

Using a local low rank plus sparse reconstruction to accelerate dynamic hyperpolarized 13C imaging using the bSSFP sequence

Eugene Milshteyn a,b, Cornelius von Morze a, Galen D Reed c, Hong Shang c, Peter J Shin a, Peder EZ Larson a,b, Daniel B Vigneron a,b,*
PMCID: PMC6054792  NIHMSID: NIHMS963014  PMID: 29567434

Abstract

Acceleration of dynamic 2D (T2 Mapping) and 3D hyperpolarized 13C MRI acquisitions using the balanced steady-state free precession sequence was achieved with a specialized reconstruction method, based on the combination of low rank plus sparse and local low rank reconstructions. Methods were validated using both retrospectively and prospectively undersampled in vivo data from normal rats and tumor-bearing mice. Four-fold acceleration of 1–2 mm isotropic 3D dynamic acquisitions with 2–5 s temporal resolution and two-fold acceleration of 0.25–1 mm2 2D dynamic acquisitions was achieved. This enabled visualization of the biodistribution of [2-13C]pyruvate, [1-13C]lactate, [13C, 15N2]urea, and HP001 within heart, kidneys, vasculature, and tumor, as well as calculation of high resolution T2 maps.

Keywords: 13C, Hyperpolarized, SSFP, Local low rank, Sparse

1. Introduction

The advent of dissolution dynamic nuclear polarization (dDNP) of 13C substrates [1], in conjunction with magnetic resonance imaging (MRI), has provided a new approach for studying the metabolic and physiological changes associated with various diseases, including cancer and diabetes, among several other examples [2–7]. Recent successful phase I and phase II clinical trials have demonstrated how dynamic imaging of 13C substrates can provide several quantifiable biomarkers of disease [8–13]. A key tradeoff in the design of dynamic hyperpolarized 13C (HP 13C) imaging strategies is the balance between spatial and temporal resolution due to the limited lifetime of the hyperpolarized magnetization, which is consistently depleted due to T1 and T2 decay, metabolism, and application of RF pulses. This tradeoff can lead to poor image quality (i.e. with large partial volume effects) and associated difficulties in model fitting of the dynamics. Balanced steady-state free precession (bSSFP) supports high resolution acquisitions by exploiting the long T2’s of 13C substrates, but may be especially affected by early depletion of the HP magnetization due to the high number of RF pulses required to achieve high resolution volume imaging [14–18]. While bSSFP does provide the highest SNR per unit time [19] and has been used for 2D HP 13C T2 mapping and 3D single time-point acquisitions [14,20,21], it has not been readily applied to 3D dynamic HP 13C acquisitions [15], especially at clinical field strengths, because of the aforementioned tradeoff in spatial and temporal resolution.

Compressed sensing has been increasingly applied for accelerating MRI by exploiting data sparsity in an appropriate domain [22–26]. Alternatively, global low rank and local low rank matrix completion has also been utilized in reconstruction of undersampled dynamic MRI data by exploiting the spatiotemporal correlations that exist within different tissues [27–30]. Both approaches have been well documented in proton imaging and have been extended to hyperpolarized 13C imaging to improve both spatial and temporal resolution [31–34]. Recently, Otazo et al. [35] showed the advantage of combining these methods into a low rank plus sparse (L+S) reconstruction in order to increase imaging speed in dynamic proton imaging since the L+S model offered higher compressibility compared to either method alone. Perfusion imaging in particular features local low rank properties that lead to improved reconstructions, since neighboring tissues have similar spatiotemporal dynamics, and these properties have been successfully exploited in initial proton perfusion imaging studies [36,37]. Likewise, combining the L+S model and the local low rank method into a local low rank plus sparse (LLR+S) model also has the potential to improve reconstruction of dynamic imaging of the biodistribution of HP 13C probes (i.e. for HP 13C perfusion imaging).

The goal of this study was to accelerate both 2D and 3D T2 mapping and 3D dynamic high resolution imaging with the bSSFP sequence using a LLR+S algorithm. In-plane resolutions of <1 mm2 were achieved for 2D T2 mapping of multiple HP 13C compounds, with 3D 1 mm isotropic T2 map demonstrated as well. Furthermore, 3D 1.5–2 mm isotropic imaging with 2–5 s temporal resolution was achieved in both healthy rats and tumor-bearing mice. Biodistribution of [2-13C]pyruvate, [1-13C]lactate, HP001, and [13C, 15N2]urea was visualized within kidneys, vasculature, heart, and tumor.

2. Theory

Otazo et al. [35] provided a formal treatment on the L+S decomposition and how it can be applied to 1H acquisitions. Dynamic 1H MRI can be separated into a low rank component representing the static background and a sparse component representing the rapid changing dynamics. HP 13C MRI, however, lacks a background signal due to the low signal of any natural abundance 13C, and the HP signal inherently rapidly decays away towards thermal equilibrium. Therefore, HP 13C acquisitions cannot truly be represented by a separation of a static background and rapidly changing dynamics since there is no incoherence between the low rank and sparse components. However, as previously mentioned, if only L+S is of interest, as is the case here, then this algorithm still outperforms a low rank or sparse only reconstruction.

The LLR+S matrix decomposition can be formulated as [35,36]:

minL,S12‖E(L+S)−d‖22+λL∑i=1Nb‖BiL‖∗+λS‖TS‖1 (1)

where L and S are the outputted decomposed low rank and sparse matrices, respectively, E is the encoding operator that performs a spatial partial Fourier transform (FT) for each time-point, d is the undersampled k-t data, Bi is an operator that selects an image block b and transforms it into a spatiotemporal matrix (assuming the spatiotemporal image data can be divided into Nb image blocks), T is the sparsifying transform for S, and λL and λS act as tuning parameters controlling the contribution of the nuclear norm and L1-norm terms, respectively.

The optimization problem in Eq. (1) was solved using iterative soft thresholding as described in Otazo et al. [35], with slight modifications to account for the local low rank approach. Briefly, for each iteration k, given the matrix M = L + S, a soft thresholding operator, defined as

Λλ(χ)=χ|χ|max(|χ|−λ,0), (2)

was applied to the singular values of Mk−1 − Sk−1 and the sparse transform coefficients of Mk−1 − Lk−1 to calculate Lk and Sk, respectively, leading to a calculation of a new Mk by enforcing data consistency. The algorithm iterated until the relative change in the solution was less than a certain tolerance limit, which depended on the specific acquisition employed. The first ten iterations were performed using the singular value decomposition (SVD) of the full spatiotemporal matrix (Global Low Rank or GLR) [29], while subsequent iterations utilize the SVD of the individual image blocks (local low rank or LLR). This helped speed up the reconstruction and improve the reconstruction time, with the number 10 chosen based on retrospective simulations. Furthermore, a cooling method was used to converge similar to previous work [29], where μ was initialized to equal λL for the first ten iterations, followed by 2*λL for the next ten iterations, followed by back to λL for the rest of the iterations. The size of the image blocks (bsize) was defined for each dataset based on the acquired matrix size. λL and λS were selected in an empirical manner [35] for the 3D dynamic and 2D T2 mapping acquisitions using the retrospectively undersampled datasets (75% undersampling) discussed in Section 3.4. Table 1 summarizes the proposed LLR+S algorithm using pseudo-code, with Ω defined as the set of image blocks that a spatiotemporal image can be divided into.

Table 1.

Pseudo-code for LLR+S reconstruction algorithm.

Inputs: y: undersampled k-t data
E: partial spatial Fourier transform operator based on undersampling mask
T: sparsifying transform
λL: singular value threshold
λS: sparsity threshold
b: image block in Ω for local low rank soft thresholding
Tol: relative change of solution
Outputs: L, S: solutions to Eq. (1); low rank and sparse components of reconstructed data
Algorithm: M0 = E*y, S0= 0% Initialize data
do {
% Singular Value Soft Thresholding
Lk = ∪b∈ΩSVTλL (Cb(Mk−1 − Sk−1))
% Soft Thresholding in T domain
Sk = T−1(ΛλS (T(Mk−1 − Lk−1)))
% Data consistency: subtract residual
Mk = Lk + Sk − E* (E(Lk + Sk) − y)
err=‖Lk+Sk−(Lk−1+Sk−1)2‖‖Lk−1+Sk−1‖2
} while err > Tol
Soft Thresholding Operator:
Λλ(χ)=χ|χ|max(|χ|−λ,0)
Singular Value Thresholding (SVT) Operator: SVTλ (M) = UΛλ (Σ)V, where [U, Σ, V] = SVD(M)
Open in a new tab

3. Methods

3.1. Animal handling

All animal studies were done under protocols approved by the University of California San Francisco Institutional Animal Care and Use Committee (IACUC). Normal Sprague-Dawley rats and transgenic adenocarcinoma of mouse prostate (TRAMP) mice [38] were used in these studies. Isoflurane (1.5%) was used to anesthetize the animals, which were then placed in a supine position on a heated pad throughout the duration of the experiments. After polarization and dissolution, each of the compounds were injected into the animal via tail vein catheters: ~3 mL over 12 s for each rat and ~500 µL over 15 s for the mouse.

3.2. Hardware and hyperpolarization

All experiments were performed on a 3 T GE MR750 clinical scanner (GE Healthcare, Waukesha, WI) with multinuclear capability. Dual-tuned 1H/13C transceiver volume radiofrequency coils were used that had either an inner diameter of 8 cm for rats or an inner diameter of 5 cm for mice.

Stock solutions of all compounds used in this study ([2-13C] pyruvate, [1-13C]lactate, [13C, 15N2]urea, HP001) were prepared as described previously [14,39]. Each compound was individually polarized in a HyperSense dissolution DNP instrument (Oxford Instruments) operating at 1.35 K and 3.35 T to achieve polarizations of ~15–20% for each compound. The compounds were then dissolved in appropriate media: 4.5 mL of 80 mM NaOH/40 mM Tris buffer for [2-13C]pyruvic acid resulting in 80 mM [2-13C]pyruvate (hereafter referred to as C2-pyruvate); 4.5 mL of 160 mM NaOH/40 mM Tris buffer for [1-13C]lactic acid resulting in 160 mM [1-13C]lactate (hereafter referred to as lactate); 5 mL of 1× phosphate-buffered saline for [13C, 15N2]urea resulting in 110 mM [13C, 15N2]urea (hereafter referred to as urea); and 5 mL of 1× phosphate-buffered saline for HP001 resulting in 100 mM HP001.

3.3. bSSFP sequence

All acquisitions used a custom bSSFP sequence with either one (2D, T2 mapping) or two (3D) phase encoding dimensions for dynamic high resolution imaging. A prior publication provides a general description of the T2 mapping sequence [14]. For all acquisitions k-space was acquired in sequential fashion. For each time-point in the 3D acquisition, α/2-TR/2 preparation pulses were played for signal stabilization, and α-TR-α/2-TR/2 flip back pulses were played at the end of each time-point for storing the remaining magnetization on the longitudinal axis.

A basic 1.6 ms time-bandwidth product (TBW) 4 Sinc RF pulse was used for all acquisitions. Frequency and power calibration was performed on a 1 mL enriched [13C]urea vial phantom (6.0 M), which was placed on top of the animal. For anatomical reference, 3D bSSFP proton images (16 × 8 × 4.8 cm, 256 × 128 × 80, 5.1 ms TR, 50° flip angle) were acquired.

3.4. Retrospective simulations

Three previously acquired datasets were used for retrospective undersampling simulations of the 3D dynamic acquisition (here-after designated as 3D Dataset 1, 2 and 3, respectively, and shown in Supporting Fig. 1A, B, and C, respectively). Specifically, these consisted of: (1) A 3D bSSFP acquired urea dataset in rat kidneys that was transformed into a 4D dataset by applying signal dynamics based on previously published HP 13C studies [40,41], (2) An EPI acquired [1-13C]pyruvate dataset in rat kidneys [42], and (3) An EPI acquired [1-13C]pyruvate dataset in TRAMP tumor. Since the LLR+S reconstruction was performed for each frequency encode (× location) individually after an FFT along the frequency encode direction (described further in Section 3.6), one slice corresponding to an × location from each 3D dataset (either containing kidneys or tumor) was used for retrospective simulations. This slice would serve as a representation of how the reconstruction would perform when applied to all × locations in the prospective acquisitions. Similarly, two previously acquired T2 mapping datasets, urea [20] and lactate [14], were used for retrospective undersampling and reconstruction with the LLR+S model (hereafter designated as T2 Mapping Dataset 1 and 2, respectively, and can be seen in Supporting Fig. 1D and E, respectively). Each subsequent retrospective simulation was assessed using the structural similarity index (SSIM) [43] and normalized root mean squared error (nRMSE), which was calculated according to the following formula [32]:

nRMSE=1n∑i=1n(χrecon,i−χoriginal,i)21n∑i=1n(χoriginal,i)2 (3)

where xrecon is the reconstructed dataset and xoriginal is the fully sampled original dataset (ground truth).

The variable-density undersampling patterns in this study were designed with a Monte Carlo simulation [22], with a high density in the k-space center. The following function was used to generate the density distribution: (1 − r)^p, where r is the radius of the k-space center, and p is the power of the polynomial. We used the polynomial variable density sampling scripts from the sparseMRI package (http://people.eecs.berkeley.edu/~mlustig/Software.html) to generate the sampling patterns for this study. To maximize incoherent aliasing along the spatiotemporal dimensions, a different pattern was designed for each time-point. An example pattern depicting 75% undersampling of ky-kz-t space, which was used in the 3D dynamic imaging, is shown in Fig. 1A and an example pattern depicting 50% undersampling of ky-t space, which was used in T2 mapping, is shown in Fig. 1B.

Fig. 1.

Fig. 1

Open in a new tab

Depiction of undersampling patterns used for the (A) 3D dynamic and (B) 2D dynamic acquisitions. The 3D dynamic acquisitions were undersampled in ky-kz-t space with different variable-density patterns and fully sampled k-space centers, with 4 time-points shown above (acquired points in black/red/green/blue). The 2D dynamic acquisitions were similarly undersampled, but in ky-t space. Each acquired point within the patterns represents a frequency encoded line of k-space. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Initial retrospective simulations focused on testing the proper sparse transform and block sizes needed for reconstruction [24], and the compressibility of each 3D dataset [35]. We tested the following sparsifying transforms: (wavelet along time (Wavelet), principle component analysis (PCA), temporal FFT (TempFFT), and total variation (TV)). To determine an appropriate transform, each sparsifying transform was applied to each dataset, and only the top 10% of the resulting coefficients were retained to compare to the ground truth. In addition to validating the sparsifying transform, the appropriate block size for the LLR+S reconstruction was tested based on the different matrix sizes used for T2 mapping and 3D dynamic imaging. For each dataset, different block sizes were applied as part of the LLR+S reconstruction using a 75% undersampling pattern, with the resulting reconstructions again compared to the ground truth using nRMSE and SSIM. Compressibility of each dataset was tested using five different models: global low rank (GLR) only, local low rank (LLR) only, global low rank plus sparse (L+S), sparse only, and local low rank plus sparse (LLR+S). The data compression was performed based on the method described in Otazo et al. for the low-rank, sparse, and low rank plus sparse models. The LLR and LLR+S models here were compressed using the method for the low rank and low rank plus sparse models, respectively, with the low rank compression applied to different image blocks. After determining the appropriate sparse transform and block size, for all 3D datasets, undersampling patterns using 10–90% of the data were designed and used in retrospective simulations to measure at what point the reconstruction begins to breakdown, in a similar fashion as described previously [32].

For the T2 mapping datasets, only compressibility was retrospectively simulated as part of these initial studies. PCA was used as the sparsifying transform based on previous accelerated T2 mapping acquisitions [24], and 50% undersampling was employed to verify that the undersampled data can be properly reconstructed and the subsequently calculated T2 maps matched up with the ground truth. The block sizes were set to 5 × 5 based on the results of the retrospective simulations.

3.5. In vivo hyperpolarized studies

The prospective 3D dynamic imaging was acquired in three normal Sprague-Dawley rats and one TRAMP mouse for C2-pyruvate, lactate and urea. The rat acquisition with urea had the following parameters: 12 × 6 × 1.8 cm3 FOV covering the kidneys, 80 × 40 × 12 matrix size for 1.5 mm isotropic resolution, TR/TE of 7.5 ms/3.75 ms, α = 30° flip angle, 60% undersampling, 13 time-points, 5 s temporal resolution, and the scan starting at the beginning of injection. The rat acquisition with C2-pyruvate had the following parameters: 12 × 6 × 1.8 cm3 FOV covering the kidneys, 60 × 30 × 9 matrix size for 2 mm isotropic resolution, TR/TE of 7.5 ms/3.75 ms, α = 30° flip angle, 60% undersampling, 13 time-points, 5 s temporal resolution, and the scan starting at the beginning of injection. The rat acquisition with lactate had the following parameters: 12 × 6 × 1.8 cm3 FOV covering the kidneys, 80 × 40 × 12 matrix size for 1.5 mm isotropic resolution, TR/TE of 6.4 ms/3.2 ms, variable flip angle, 75% undersampling, 13 time-points, 3 s temporal resolution, and the scan starting 15 s after the beginning of injection. The mouse acquisition for all three compounds had the following parameters: 6 × 3 × 3 cm3 FOV covering the tumor, 40 × 20 × 20 matrix size for 1.5 mm isotropic resolution, TR/TE of 6.4 ms/3.2 ms, variable flip angle, 75% undersampling, 16 time-points, 2 s temporal resolution, and the scan starting 15 s after the beginning of injection.

Initial 3D prospectively undersampled T2 mapping of urea acquisitions had the following parameters: 12 × 6 × 1.8 cm3 FOV covering the kidneys, 1–2.5 mm isotropic resolution, TR/TE of 6.4 ms/3.2 ms, α = 180° flip angle, 75% undersampling, 20 time-points, and the scan starting 30 s after the beginning of injection.

The 2D prospectively undersampled T2 mapping was acquired in three normal Sprague-Dawley rats for all compounds. All acquisitions were performed in projection mode (no slice-select gradient). C2-pyruvate, lactate, and HP001 acquisitions had the following parameters: 14 × 7 cm2 coronal FOV covering heart and abdomen, 140 × 70 matrix size for 1 mm2 in-plane resolution, TR/TE of 8.5 ms/4.25 ms, α = 180° flip angle, 50% undersampling, 20 time-points, and the scan starting 30 s after the beginning of injection. Urea acquisitions had the following parameters: 14 × 7 cm2 coronal FOV heart and abdomen, 280 × 140 matrix size for 0.25 mm2 in-plane resolution, TR/TE of 12.5 ms/6.25 ms, α = 180° flip angle, 50% undersampling, 20 time-points, and the scan starting 30 s after the beginning of injection. Fully sampled acquisitions of HP001 and urea were acquired at the same time as the undersampled acquisitions for comparison and had the following parameters: 14 × 7 cm2 coronal FOV heart and abdomen, 140 × 70 matrix size for 1 mm2 in-plane resolution, TR/TE of 8.5 ms/4.25 ms, α = 180° flip angle, 20 time-points, and the scan starting 30 s after the beginning of injection.

3.6. Image reconstruction

Reconstruction of all datasets used the same sparse transform and block sizes for the LLR+S retrospective reconstructions. For the 3D dynamic and 3D T2 mapping acquisitions, the data was Fourier transformed along the readout (frequency encode) dimension to x-ky-kz-t and the LLR+S algorithm was subsequently applied to each × location separately, while for 2D T2 mapping the algorithm was applied to kx-ky-t. λL, λS, and the tolerance limit for the 3D dynamic and 3D T2 mapping acquisitions were 0.01, 0.001, and 0.0015, respectively. λL, λS, and the tolerance limit for the 2D T2 mapping acquisitions were 0.1, 0.001, and 0.004, respectively. The total reconstruction time in MATLAB (The MathWorks, Inc., Natick, MA) on a Linux Workstation with a 3.07 GHz quadcore Intel Xeon CPU was approximately 10 min for 3D dynamic acquisitions and approximately 2 min for 2D T2 mapping acquisitions. The reconstruction of the 3D dynamic acquisitions used the Parallel Computing Toolbox in MATLAB since the reconstruction at each × location could be treated independently from one another. Sample MATLAB code showing example retrospective and prospective reconstructions can be found in the recon section of the Hyperpolarized MRI Toolbox (https://github.com/LarsonLab/hyperpolarized-mri-toolbox).

4. Results

4.1. LLR+S reconstruction of retrospective simulations

4.1.1. Temporal sparsity and bsize

Table 2 shows the nRMSE and SSIM of the four different temporal sparse transforms for all three retrospectively undersampled 3D datasets after transformation and retention of the top 10% of coefficients. PCA outperformed the other three for all datasets and was used in subsequent simulations and reconstructions.

Table 2.

Comparison of the different sparsifying transforms on all three 3D retrospectively undersampled datasets. Comparison to the ground truth was done after retaining only the top 10% of sparsifying coefficients.

TempFFT Wavelet TV PCA
3D Dataset 1
nRMSE 0.3638 0.2968 0.4983 0.2712
SSIM 0.7053 0.7486 0.6484 0.7586
3D Dataset 2
nRMSE 0.1944 0.1562 0.3016 0.092
SSIM 0.6772 0.6618 0.6138 0.8941
3D Dataset 3
nRMSE 0.1497 0.1777 0.3614 0.0631
SSIM 0.7581 0.7177 0.5875 0.88
Open in a new tab

Table 3 shows the nRMSE and SSIM for the different block sizes that were tested for each retrospectively undersampled 3D dataset. The block sizes that resulted in the lowest nRMSE were about ~1/5–1/4 the size of the matrix for the phase encode direction and were used in subsequent retrospective simulations: 8 × 3 for the 40 × 12 matrix sizes used in 3D Datasets 1 and 2; 5 × 5 for the 20 × 20 matrix sizes used in 3D Dataset 3.

Table 3.

Comparison of different block sizes (bsize) used in the LLR+S reconstruction for all three 3D retrospectively undersampled datasets. The PCA transform was used for all comparisons.

bsize 4,2 5,3 6,3 8,3 10,3 20,6
3D Dataset 1
nRMSE 0.1177 0.0995 0.1129 0.0908 0.1095 0.2702
SSIM 0.9329 0.9475 0.9368 0.9543 0.9455 0.8788
bsize 4,2 5,3 6,3 8,3 10,3 20,6
3D Dataset 2
nRMSE 0.1502 0.1392 0.1429 0.1344 0.1385 0.2161
SSIM 0.9126 0.9187 0.9176 0.9239 0.9215 0.9047
bsize 2,2 4,4 5,5 10,10
3D Dataset 3
nRMSE 0.1327 0.0913 0.0848 0.1301
SSIM 0.954 0.9631 0.9643 0.9482
Open in a new tab

4.1.2. Comparison of reconstruction algorithms

The top row of Fig. 2 depicts the nRMSE vs. compression ratio for the retrospectively undersampled 3D datasets with the five different types of reconstruction algorithms. The LLR+S method showed the lowest nRMSE across multiple compression ratios for all the retrospectively undersampled 3D datasets, indicating the highest percent undersampling can be achieved when using that algorithm. The bottom row of Fig. 2 depicts the nRMSE vs. percent undersampling for the retrospectively undersampled 3D datasets reconstructed with LLR+S. Based on the results for all the datasets, >75% undersampling was deemed the point where the reconstruction began to fail as the nRMSE began rising rapidly past that point, indicating severe distortion from the ground truth after reconstruction. Fig. 3 shows an example result from a reconstruction of 3D dataset 1 with 75% undersampling, where one slice of the reconstruction is shown compared to the ground truth slice and zero-filled slice, along with the difference map between the ground truth and reconstruction, and representative dynamic curves from the vasculature and kidneys. The difference map and dynamic curves, along with visual inspection of the slices show that the reconstruction successfully eliminated undersampling artifacts and recovered the original signal.

Fig. 2.

Fig. 2

Open in a new tab

Different undersampling factors were used to test the capability of the LLR+S reconstruction for all three retrospectively undersampled 3D datasets. Parts A–C depict the nRMSE vs. compression ratio for the three retrospectively undersampled 3D datasets, respectively, with the five different types of reconstruction algorithms. For all three datasets, the LLR+S method showed the lowest nRMSE across multiple compression ratios, indicating the highest percent undersampling can be achieved when using that algorithm. Parts D–F depict the nRMSE vs. percent undersampling for all three retrospectively undersampled 3D datasets reconstructed with LLR+S, respectively, with >~75% undersampling being the point where the reconstruction begins to considerably breakdown.

Fig. 3.

Fig. 3

Open in a new tab

An example reconstruction of 3D dataset 1 (B) with 75% undersampling can be seen here compared to the ground truth (A), along with the difference image (C), zerofilled reconstruction (D), overlay of depicted carbon slice onto a 1H image (E), and comparison of dynamic curves between the ground truth, LLR+S reconstruction, and the zero-filled reconstruction for the vasculature (F) and kidney (G). The LLR+S reconstruction matches up closely with the ground truth based on the difference image, qualitative observation and the dynamic curves, while the zero-filled reconstruction has severe aliasing. All images were scaled from 0 to 1.

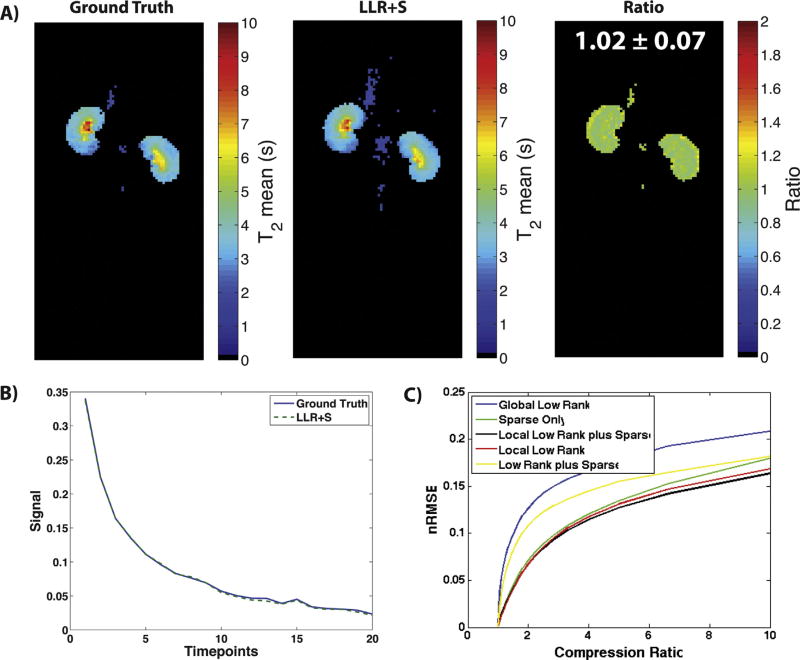
Fig. 4A shows the resulting T2 maps after retrospective 50% undersampling and reconstruction of T2 Mapping Dataset 1. The LLR+S reconstruction matched up well with the ground truth qualitatively, as well as based on the ratio between the two maps being equal ~1 and the representative signal decay curves in Fig. 4B. Fig. 4C shows similar results to Fig. 2A–C, whereby the LLR+S method showed the lowest nRMSE across multiple compression ratios for the T2 Mapping Dataset 1, indicating the highest percent undersampling can be achieved when using that algorithm.

Fig. 4.

Fig. 4

Open in a new tab

The LLR+S reconstruction was tested on retrospective T2 Mapping Dataset 1. The LLR+S reconstruction matches up with the fully sampled ground truth as evidenced by the ratio map being equal ~1 (A). Furthermore, representative decay curves (B) from the ground truth and LLR+S match up very well. Part C shows the nRMSE vs. compression ratio for T2 Mapping Dataset 1, with the LLR+S reconstruction showing better compressibility compared to other reconstruction algorithms.

4.2. LLR+S reconstruction of prospective 3D dynamic acquisitions

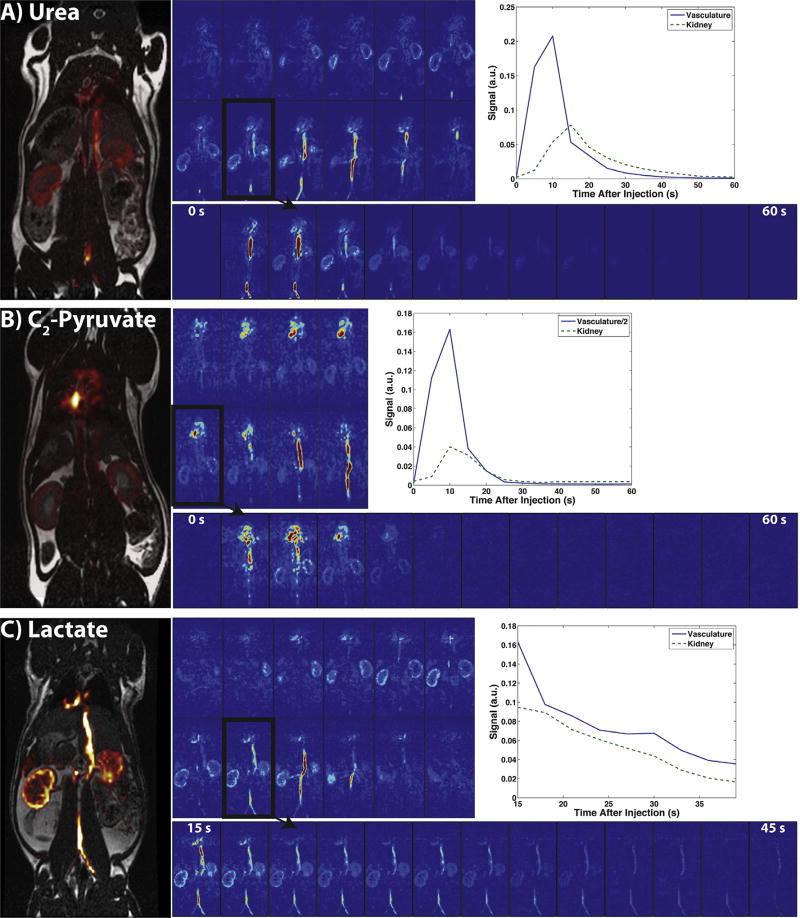
Fig. 5 shows the reconstructions of the prospective in vivo urea (A), lactate (B), and C2-pyruvate (C) datasets acquired in rats. Each part shows a 3D view of one time-point, all time-points of a representative kidney slice (outlined in black), representative vascular and kidney dynamic curves, and a carbon overlay on the 1H anatomical image. The LLR+S algorithm successfully reconstructed both 60% and 75% undersampled datasets, with the dynamic curves matching up with expected in vivo dynamics [40,41,44,45] for all three compounds in healthy rat kidneys and vasculature. The SNR was high enough for 3D visualization for around 30 s after the start of the scan (2nd–7th time-point) for the urea and C2-pyruvate acquisitions, and considerably longer in the lactate acquisition with the use of a variable flip angle scheme and later scan start time.

Fig. 5.

Fig. 5

Open in a new tab

Depiction of the urea (A), C2-pyruvate (B), and lactate (C) uptake and biodistribution of the 3D dynamic acquisition in one Sprague-Dawley rat. The full 3D view of each compound at 15 s and in one slice (outlined in black) dynamically from 0 to 60 s (15–54 s in lactate) indicates uptake in vasculature, kidneys, and heart. The dynamics in the vasculature and the kidneys can also be seen on the top right of each part, along with carbon overlays of the outlined slice on top of anatomical 1H images on the left.

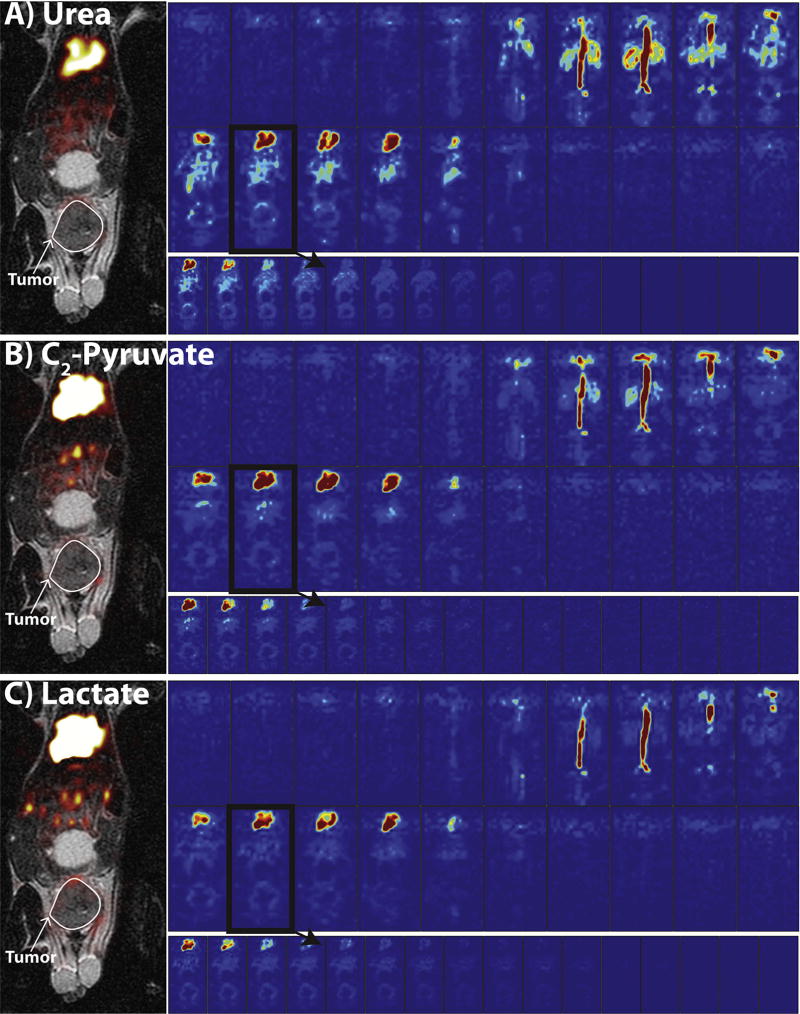
Fig. 6 shows the reconstructions of the prospective in vivo urea (A), lactate (B), and C2-pyruvate (C) datasets acquired in a tumor-bearing mouse. As with Fig. 5, each part shows a 3D view of one time-point, all time-points of a representative tumor slice (outlined in black), and a carbon overlay on the 1H anatomical image. The LLR+S algorithm successfully reconstructed the 75% undersampled datasets, with expected in vivo dynamics [14,46,47] seen for all three compounds in a TRAMP tumor. The SNR was high enough for 3D visualization for several time-points for all three compounds, even at 1.5 mm isotropic resolution.

Fig. 6.

Fig. 6

Open in a new tab

Depiction of the urea (A), C2-pyruvate (B), and lactate (C) uptake and biodistribution of the 3D dynamic acquisition in a tumor-bearing mouse. The full 3D view of each compound at 15 s and in one slice (outlined in black) dynamically from 15 to 45 s indicates uptake in vasculature, tumor periphery, kidneys, and heart. The carbon overlays of the outlined slice on top of anatomical 1H images are on the left, along with the outline of the tumor in white.

4.3. LLR+S reconstruction of prospective T2 maps

The prospective LLR+S reconstructed 2D T2 mapping acquisitions of HP001 and urea matched up well with the fully sampled acquisitions, as evidenced by the ratio maps of the fully sampled and accelerated acquisitions for urea (Fig. 7A and B) and HP001 (Fig. 7C), which had an average value of 0.89 ± 0.21 and 0.95 ± 0.23 in the kidneys and vasculature, respectively. Supporting video 1 shows all the time-points of the HP001 T2 mapping acquisition. The urea acquisition demonstrated the capability of sub-millimeter in-plane resolution acquisitions for HP probes with sufficient acceleration. The average value in the kidneys for C2-pyruvate (Fig. 8B), 0.786 ± 0.13, agreed well with previously acquired, lower resolution T2 maps [14]. The LLR+S reconstruction allowed ~6-fold improvement in resolution even with C2-pyruvate having a relatively short in vivo average T2. Additionally, both lactate (~2.43 s in kidneys) (Fig. 8A) and 3D urea T2 maps (~4.84 s in kidneys) (Fig. 8C and D) matched up well with literature values [14,20], with the 3D urea T2 map demonstrating the capability of 1 mm isotropic dynamic imaging with HP probes. Video 2 shows all the time-points from the 3D urea T2 mapping acquisition, with the signal decay matching up with the T2 map whereby the longest lasting signal appearing in the renal pelvis. Supporting videos 3 and 4 shows the all the time-points of the lactate and C2-pyruvate T2 mapping acquisitions, respectively.

Fig. 7.

Fig. 7

Open in a new tab

2-fold accelerated acquisitions of 0.5 × 0.5 mm2 urea and 1 × 1 mm2 HP001 T2 mapping are presented here. Part A shows the slices of the urea acquisition, with the signal lasting longest in the kidneys due to the long T2’s. Part B shows a zoomed-in version of the outlined slice in part A, which shows the resolution being high enough to accurately visualize the different kidney compartments. Additionally, comparison of the LLR+S reconstructed T2 map to the fully sampled 1 ~1 mm2 T2 map revealed a good agreement in calculated T2 values. The ratio map had an average of 0.89 ± 0.21 (mean ± intra-image standard deviation) within the kidneys and vasculature. Part C shows the results of the HP001 T2 mapping. Similar to the urea results, comparison to the fully sampled 1 ~1 mm2 acquisition revealed a good agreement in calculated T2 values. The ratio map had an average of 0.95 ± 0.23 (mean ± intra-image standard deviation) within the kidneys and vasculature.

Fig. 8.

Fig. 8

Open in a new tab

High resolution T2 maps for other substrates, such as lactate (A) and C2-pyruvate (B), are shown here. The accelerated acquisitions had high enough spatial resolution to visualize the substrate in kidney, heart, and vasculature, with the mean T2 values matching up well with previously acquired T2 maps. The slice by slice T2 map (C) and maximum intensity projection representation (D) from the urea 3D 1 mm isotropic T2 mapping acquisition show clear delineation of renal cortex, medulla, pelvis, and vasculature, with the T2 distribution matching up with literature values. Only 6 representative slices (out of 18) are shown in part C, while the maximum intensity projection in part D is from all slices.

Video 2.

Video 2

Open in a new tab

The dynamics of the urea over the course of the 3D 1 mm isotropic T2 mapping acquisition can be seen in the accompanying video. Each 360° rotation signifies one time-point, with the temporal resolution of the acquisition being 2.3 s. The signal decays rapidly outside the kidneys, and lasts the longest within the renal pelvis, which is known to have the longest T2 values.

5. Discussion

With the current desire for high spatiotemporal coverage of hyperpolarized 13C compounds, especially with recent successful clinical human studies that require large FOVs, the need for accelerated acquisitions with sub-Nyquist sampling strategies and accompanying reconstructions is evident. Low rank plus sparse and local low rank reconstruction strategies have been previously employed in undersampled dynamic 1H acquisitions. We demonstrated the development and application of the local low rank plus sparse algorithm for reconstruction of undersampled 3D dynamic and 2D/3D T2 mapping hyperpolarized 13C acquisitions with the bSSFP sequence. The algorithm allowed for up to ~75% undersampling depending on the particular acquisition, with the acceleration factor providing considerably faster effective echo times for high SNR acquisitions. We were able to achieve previously unseen 2D sub-millimeter and 1–1.5 mm 3D isotropic spatial resolutions with 2–5 s temporal resolutions and considerable temporal windows.

Due to the nonrecoverable nature of the hyperpolarized magnetization, the number of phase encoding steps done in HP 13C imaging acquisitions is considerably smaller than 1H imaging acquisitions, which limits the amount of undersampling possible. The bSSFP sequence is an attractive choice for acceleration since the spatial resolution and matrix sizes approach that of 2D high resolution 1H imaging. Additionally, translating this sequence into the clinic will require much larger matrix sizes to achieve sub-cm spatial resolution due to the larger FOVs, which may allow for higher acceleration factors beyond what has been shown in this study. Based on previous 1H studies with local low rank and low rank plus sparse reconstructions, the algorithm presented here can be easily combined with parallel imaging and other types of imaging sequences, including echo-planar, spiral, and radial imaging [28,29,35,48]. Other types of reconstructions can be further evaluated and compared to the LLR+S algorithm, including multi-scale low rank [49] and model-based/dictionary learning [50]. Furthermore, the results presented here depict the LLR+S reconstruction working for different approaches for dynamic acquisitions, which can be optimized in general depending on the type of biological information desired. For example, the 3D dynamic urea and C2-pyruvate sequences began at the start of injection and were acquired for 60 s, and represent acquisitions looking at potentially perfusion, biodistribution, and uptake of the injected substrate. The 3D dynamic lactate sequence began after the end of injection and was only acquired for 39 s, but provided higher SNR due to both a shorter acquisition window and the use of a variable flip angle scheme.

There are several potential applications of the developed high spatial resolution 2D T2 mapping and 3D dynamic acquisitions with regards to hyperpolarized 13C imaging in general, and specifically with regards to the compounds utilized in this study. First, we believe the T2 mapping can have multiple roles in both preclinical and clinical studies, including understanding the distribution of T2’s within the anatomy of interest for a given compound and distinguishing between healthy and diseased tissue, as is currently performed in 1H imaging [51]. The distribution of T2’s will help sequence development and optimization, as well as analysis, as more and more compounds are developed and translated into humans. Quantitative T2 mapping has already been performed with HP 13C compounds [21], and can be readily translated to clinical exams, especially with the LLR+S reconstruction since larger FOVs would be required. Second, we believe the 3D dynamic acquisition can be readily translated into humans for acquisitions featuring the compounds used in this study. Urea and HP001 would allow for high spatial resolution calculations of perfusion [40,46,47] and glomerular filtration rate [52,53]. C2-pyruvate and lactate could represent a different approach to looking at metabolism, whereby the distribution and dynamics of each compound would reflect conversion to other metabolites. Furthermore, knowing the biodistribution of these compounds at a high spatial resolution in humans could be informative for developing the acquisitions for clinical studies.

Future work will focus on optimizing the acquisitions presented here with improved flip angle schemes to maximize SNR over the entire temporal window, and incorporate spectrally selective pulses for accelerated metabolic imaging of [1-13C]pyruvate. As discussed previously in Otazo et al. [35], the L+S sum represents the image reconstruction and the individual background and dynamic components are less important. In the case of hyperpolarized 13C imaging, since the signal is always decaying away back to equilibrium due to various processes, there is no explicit separation of slowly-varying background and dynamic components as can be found in cardiac perfusion, for example. However, further evaluation is needed on what information may be obtained from the individual L and S components that result from running the algorithm. Based on the simulations above, the sum of L and S out-performed other reconstructions, and was consequently the focus of this study.

6. Conclusion

In this study, we implemented and tested a local low rank plus sparse reconstruction algorithm to accelerate hyperpolarized 13C imaging with the balanced steady-state free precession sequence. We were able to acquire 3D images with high spatiotemporal resolution in healthy rat kidneys and tumor-bearing mice, as well as high spatial resolution 2D and 3D T2 maps of multiple hyperpolarized substrates. Future work will focus on adapting the reconstruction algorithm for parallel imaging and translation into clinical studies.

Supplementary Material

Figure S1
Video 1

Video 1. All time-points from the 2-fold accelerated 1 × 1 mm2 HP001 T2 Mapping acquisition used in the analysis (some cutoff due signal over-ranging).

Download video file (46.5KB, mov)
Video 2

Video 2. The dynamics of the urea over the course of the 3D 1 mm isotropic T2 mapping acquisition can be seen in the accompanying video. Each 360° rotation signifies one time-point, with the temporal resolution of the acquisition being 2.3 s. The signal decays rapidly outside the kidneys, and lasts the longest within the renal pelvis, which is known to have the longest T2 values.

Download video file (1.5MB, mov)
Video 3

Video 3. All time-points from the 2-fold accelerated 1 × 1 mm2 lactate T2 Mapping acquisition used in the analysis (some cutoff due signal over-ranging).

Download video file (37.9KB, mov)
Video 4

Video 4. All time-points from the 2-fold accelerated 1 × 1 mm2 C2-pyruvate T2 Mapping acquisition used in the analysis (some cutoff due signal over-ranging).

Download video file (51KB, mov)

Video 1.

Video 1

Open in a new tab

All time-points from the 2-fold accelerated 1 × 1 mm2 HP001 T2 Mapping acquisition used in the analysis (some cutoff due signal over-ranging).

Video 3.

Video 3

Open in a new tab

All time-points from the 2-fold accelerated 1 × 1mm2 lactate T2 Mapping acquisition used in the analysis (some cutoff due signal over-ranging).

Video 4.

Video 4

Open in a new tab

All time-points from the 2-fold accelerated 1 × 1mm2 C2-pyruvate T2 Mapping acquisition used in the analysis (some cutoff due signal over-ranging).

Acknowledgments

We gratefully acknowledge Dr. Peng Cao, Dr. Robert Bok, Lucas Carvajal, and Mark van Criekinge for all their help, as well as grant support from NIH P41EB013598 and R01EB013427. NIH K01DK099451 supported CVM.

Footnotes

Appendix A. Supplementary material

Supplementary data associated with this article can be found, in the online version, at https://doi.org/10.1016/j.jmr.2018.03.006.

References

  • 1.Ardenkjaer-Larsen JH, Fridlund B, Gram A, Hansson G, Hansson L, Lerche MH, Servin R, Thaning M, Golman K. Increase in signal-to-noise ratio of >10,000 times in liquid-state NMR. Proc. Natl. Acad. Sci. USA. 2003;100:10158–10163. doi: 10.1073/pnas.1733835100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2.Kurhanewicz J, Vigneron DB, Brindle K, Chekmenev EY, Comment A, Cunningham CH, Deberardinis RJ, Green GG, Leach MO, Rajan SS, Rizi RR, Ross BD, Warren WS, Malloy CR. Analysis of cancer metabolism by imaging hyperpolarized nuclei: prospects for translation to clinical research. Neoplasia. 2011;13:81–97. doi: 10.1593/neo.101102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Golman K, Petersson JS. Metabolic imaging and other applications of hyperpolarized 13C1. Acad. Radiol. 2006;13:932–942. doi: 10.1016/j.acra.2006.06.001. [DOI] [PubMed] [Google Scholar]
  • 4.Brindle KM, Bohndiek SE, Gallagher FA, Kettunen MI. Tumor imaging using hyperpolarized resonance spectroscopy 13C magnetic. Magn. Reson. Med. 2011;66:505–519. doi: 10.1002/mrm.22999. [DOI] [PubMed] [Google Scholar]
  • 5.Wilson DM, Kurhanewicz J. Hyperpolarized 13C MR for molecular imaging of prostate cancer. J. Nucl. Med. 2014;55:1567–1572. doi: 10.2967/jnumed.114.141705. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Laustsen C, Ostergaard JA, Lauritzen MH, Norregaard R, Bowen S, Sogaard LV, Flyvbjerg A, Pedersen M, Ardenkjaer-Larsen JH. Assessment of early diabetic renal changes with hyperpolarized [1-13C]pyruvate. Diabetes. Metab. Res. Rev. 2013;29:125–129. doi: 10.1002/dmrr. [DOI] [PubMed] [Google Scholar]
  • 7.Bertelsen LB, Nielsen PM, Qi H, Nørlinger TS, Zhang X, Stødkilde-jørgensen H, Laustsen C. Diabetes induced renal urea transport alterations assessed with 3D hyperpolarized 13C, 15N-Urea. Magn. Reson. Med. 2016 doi: 10.1002/mrm.26256. [DOI] [PubMed]
  • 8.Nelson SJ, Kurhanewicz J, Vigneron DB, Larson PEZ, Harzstark AL, Ferrone M, van Criekinge M, Chang JW, Bok R, Park I, Reed G, Carvajal L, Small EJ, Munster P, Weinberg VK, Ardenkjaer-Larsen JH, Chen AP, Hurd RE, Odegardstuen L-I, Robb FJ, Tropp J, Murray JA. Metabolic imaging of patients with prostate cancer using hyperpolarized [1–13C]pyruvate. Sci. Transl. Med. 2013;5:198ra108. doi: 10.1126/scitranslmed.3006070. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Chen H, Larson PEZ, Gordon JW, Bok RA, Ferrone M, Van Criekinge M, Carvajal L, Aggarwal R, Slater JB, Park I, Milshteyn E, Nelson SJ, Kurhanewicz J, Vigneron DB. Phase II clinical hyperpolarized 13C 3Ddynamic metabolic imaging of prostate cancer using a B1-insensitive variable flip angle design. Proc. Intl. Soc. Mag. Reson. Med. 25:0725. (n.d.) [Google Scholar]
  • 10.Gordon JW, Chen H, Larson PEZ, Park I, Van Criekinge M, Milshteyn E, Bok R, Ferrone M, Slater JB, Kurhanewicz J, Vigneron DB. Human hyperpolarized C-13 MRI using a novel echo-planar imaging (EPI) approach. Proc. Intl. Soc. Mag. Reson. Med. 25:0728. doi: 10.1002/MRM26123.4. (n.d.) [DOI] [Google Scholar]
  • 11.Zhu Z, Marco-rius I, Ohliger MA, Carvajal L, Gordon JW, Chen H, Park I, Cao P, Shin PJ, Milshteyn E, Von Morze C, Ferrone M, Slater JB, Wang Z, Larson PEZ, Aggarwal R, Bok R, Kurhanewicz J, Munster P, Vigneron DB. Hyperpolarized 13C dynamic breath-held molecular imaging to detect targeted therapy response in patients with liver metastases. Proc. Intl. Soc. Mag. Reson. Med. 25:1115. (n.d.) [Google Scholar]
  • 12.Granlund KL, Vargas HA, Lyashchenko SK, Denoble PJ, Laudone V, Eastham JA, Ramon A, Kennedy M, Nicholson D, Guo YW, Chen A, Tropp J, Hricak H, Keshari KR. Utilizing hyperpolarized MRI in prostate cancer to assess metabolic dynamics and histopathologic grade. Proc. Intl. Soc. Mag. Reson. Med. 25:0727. (n.d.) [Google Scholar]
  • 13.Tyler D, Rider O, Dodd M, Lau A, Lewis A, Miller J, Peterzan M, Trumper C, Neubauer S. Demonstrating the Randle cycle in vivo: assessment of physiological alterations in human cardiac metabolism using hyperpolarised 13C MR spectroscopy. Proc. Intl. Soc. Mag. Reson. Med. 25:0726. (n.d.) [Google Scholar]
  • 14.Milshteyn E, Von Morze C, Reed GD, Shang H, Shin PJ, Zhu Z, Chen H, Bok R, Goga A, Kurhanewicz J, Larson PEZ, Vigneron DB. Development of high resolution 3D hyperpolarized carbon-13 MR molecular imaging techniques. Magn. Reson. Imag. 2017;38:152–162. doi: 10.1016/j.mri.2017.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Shang H, Sukumar S, Von Morze C, Bok RA, Marco-Rius I, Kerr A, Reed GD, Milshteyn E, Ohliger MA, Kurhanewicz J, Larson PEZ, Pauly JM, Vigneron DB. Spectrally selective three-dimensional dynamic balanced steady-state free precession for hyperpolarized C-13 metabolic imaging with spectrally selective radiofrequency pulses. Magn. Reson. Med. 2016 doi: 10.1002/mrm.26480. [DOI] [PMC free article] [PubMed]
  • 16.Svensson J, Månsson S, Johansson E, Petersson JS, Olsson LE. Hyperpolarized 13C MR angiography using trueFISP. Magn. Reson. Med. 2003;50:256–262. doi: 10.1002/mrm.10530. [DOI] [PubMed] [Google Scholar]
  • 17.Leupold J, Månsson S, Stefan Petersson J, Hennig J, Wieben O. Fast multiecho balanced SSFP metabolite mapping of 1H and hyperpolarized 13C compounds. Magn. Reson. Mater. Phys. Biol. Med. 2009;22:251–256. doi: 10.1007/s10334-009-0169-z. [DOI] [PubMed] [Google Scholar]
  • 18.Johansson E, Olsson LE, Månsson S, Petersson JS, Golman K, Ståhlberg F, Wirestam R. Perfusion assessment with bolus differentiation: A technique applicable to hyperpolarized tracers. Magn. Reson. Med. 2004;52:1043–1051. doi: 10.1002/mrm.20247. [DOI] [PubMed] [Google Scholar]
  • 19.Scheffler K, Lehnhardt S. Principles and applications of balanced SSFP techniques. Eur. Radiol. 2003;13:2409–2418. doi: 10.1007/s00330-003-1957-x. [DOI] [PubMed] [Google Scholar]
  • 20.Reed GD, Von Morze C, Bok R, Koelsch BL, Van Criekinge M, Smith KJ, Shang H, Larson PEZ, Kurhanewicz J, Vigneron DB. High resolution 13C MRI with hyperpolarized urea. Vivo T2 mapping and 15N labeling effects. IEEE Trans. Med. Imag. 2014;33:362–371. doi: 10.1109/TMI.2013.2285120. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Reed GD, von Morze C, Verkman AS, Koelsch BL, Chaumeil MM, Lustig M, Ronen SM, Bok RA, Sands JM, Larson PEZ, Wang ZJ, Larsen JHA, Kurhanewicz J, Vigneron DB. Imaging renal urea handling in rats at millimeter resolution using hyperpolarized magnetic resonance relaxometry. Tomography. 2016;2:125–137. doi: 10.18383/j.tom2016.00127. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Lustig M, Donoho D, Pauly JM. Sparse MRI: the application of compressed sensing for rapid MR imaging. Magn. Reson. Med. 2007;58:1182–1195. doi: 10.1002/mrm.21391. [DOI] [PubMed] [Google Scholar]
  • 23.Lustig M, Donoho DL, Santos JM, Pauly JM. Compressed sensing MRI: a look at how CS can improve on current imaging techniques. IEEE Signal Process. Mag. 2008;25:72–82. doi: 10.1109/MSP.2007.914728. [DOI] [Google Scholar]
  • 24.Feng L, Otazo R, Jung H, Jensen JH, Ye JC, Sodickson DK, Kim D. Accelerated cardiac T2 mapping using breath-hold multiecho fast spin-echo pulse sequence with k-t FOCUSS. Magn. Reson. Med. 2011;65:1661–1669. doi: 10.1002/mrm.22756. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Lustig M, Santos JM, Donoho D, Pauly JM. k-t SPARSE: high frame rate dynamic MRI exploiting spatio-temporal sparsity. Proc. Intl. Soc. Mag. Reson. Med. 14:2420. (n.d.) [Google Scholar]
  • 26.Jung H, Ye JC, Kim EY. Improved k–t BLAST and k– t SENSE using FOCUSS. Phys. Med. Biol. 2007;52:3201–3226. doi: 10.1088/0031-9155/52/11/018. [DOI] [PubMed] [Google Scholar]
  • 27.Trzasko J, Manduca A. Local versus global low-rank promotion in dynamic mri series reconstruction. Proc. Intl. Soc. Mag. Reson. Med. 19:4371. (n.d.) [Google Scholar]
  • 28.Zhang T, Cheng JY, Potnick AG, Barth RA, Alley MT, Uecker M, Lustig M, Pauly JM, Vasanawala SS. Fast pediatric 3D free-breathing abdominal dynamic contrast enhanced MRI with high spatiotemporal resolution. J. Magn. Reson. Imag. 2015;41:460–473. doi: 10.1002/jmri.24551. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Zhang T, Pauly JM, Levesque IR. Accelerating parameter mapping with a locally low rank constraint. Magn. Reson. Med. 2015;73:655–661. doi: 10.1002/mrm.25161. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Sarma M, Hu P, Rapacchi S, Ennis D, Thomas A, Lee P, Kupelian P, Sheng K. Accelerating dynamic magnetic resonance imaging (MRI) for lung tumor tracking based on low-rank decomposition in the spatial-temporal domain: a feasibility study based on simulation and preliminary prospective undersampled MRI. Int. J. Radiat. Oncol. Biol. Phys. 2014;88:723–731. doi: 10.1016/j.ijrobp.2013.11.217. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Larson PEZ, Hu S, Lustig M, Kerr AB, Nelson SJ, Kurhanewicz J, Pauly JM, Vigneron DB. Fast dynamic 3D MRSI with compressed sensing and multiband excitation pulses for hyperpolarized 13C studies. Magn. Reson. Med. 2011;65:610–619. doi: 10.1016/j.biotechadv.2011.08.021.Secreted. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Hu S, Lustig M, Balakrishnan A, Larson PEZ, Bok R, Nelson SJ, Goga A, Pauly JM, Vigneron DB. 3D compressed sensing for highly accelerated hyperpolarized 13C MRSI with in vivo applications to transgenic mouse models of cancer. Magn. Reson. Med. 2010;63:312–321. doi: 10.1002/mrm.22233.3D. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Gordon JW, Fain SB, Niles DJ, Johnson KM. Robust single-shot hyperpolarized 13C spectroscopic imaging utilizing incoherent k-t spiral sampling and low-rank matrix completion. Proc. Intl. Soc. Mag. Reson. Med. 22:3796. (n.d.) [Google Scholar]
  • 34.DeVience SJ, Mayer D. Speeding up dynamic spiral chemical shift imaging with incoherent sampling and low-rank matrix completion. Magn. Reson. Med. 2017;77:951–960. doi: 10.1002/mrm.26170. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35.Otazo R, Candès E, Sodickson DK. Low-rank plus sparse matrix decomposition for accelerated dynamic MRI with separation of background and dynamic components. Magn. Reson. Med. 2015;73:1125–1136. doi: 10.1002/mrm.25240. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 36.Dankova M, Rajmic P, Jirik R. Acceleration of perfusion MRI using locally low-rank plus sparse model. Latent Var. Anal. Signal. 2015 Sep;:514–521. doi: 10.1007/978-3-319-22482-4. [DOI]
  • 37.Lingala SG, Hu Y, Dibella E, Jacob M. Accelerated dynamic MRI exploiting sparsity and low-rank structure: K-t SLR. IEEE Trans. Med. Imag. 2011;30:1042–1054. doi: 10.1109/TMI.2010.2100850. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38.Hurwitz AA, Foster BA, Allison JP, Greenberg NM, Kwon ED. The TRAMP mouse as a model for prostate cancer. Curr. Protoc. Immunol. 2001;Chapter 20:Unit 20.5. doi: 10.1002/0471142735.im2005s45. [DOI] [PubMed] [Google Scholar]
  • 39.Von Morze C, Larson PEZ, Hu S, Yoshihara HA, Bok RA, Goga A, Ardenkjaer-Larsen JH, Vigneron DB. Investigating tumor perfusion and metabolism using multiple hyperpolarized 13C compounds: HP001, pyruvate and urea. Magn. Reson. Imag. 2012;30:305–311. doi: 10.1016/j.mri.2011.09.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 40.Von Morze C, Larson PEZ, Hu S, Keshari K, Wilson DM, Ardenkjaer-Larsen JH, Goga A, Bok R, Kurhanewicz J, Vigneron DB. Imaging of blood flow using hyperpolarized [13C]urea in preclinical cancer models. J. Magn. Reson. Imaging. 2011;33:692–697. doi: 10.1002/jmri.22484. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 41.von Morze C, Bok RA, Sands JM, Kurhanewicz J, Vigneron DB. Monitoring urea transport in rat kidney in vivo using hyperpolarized 13C magnetic resonance imaging. AJP Ren. Physiol. 2012;302:F1658–F1662. doi: 10.1152/ajprenal.00640.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 42.Gordon JW, Vigneron DB, Larson PEZ. Development of a symmetric echo planar imaging framework for clinical translation of rapid dynamic hyperpolarized 13C imaging. Magn. Reson. Med. 2016:1–7. doi: 10.1002/mrm.26123. [DOI] [PMC free article] [PubMed]
  • 43.Wang Z, Bovik AC, Sheikh HR, Simoncelli EP. Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process. 2004;13:600–612. doi: 10.1109/TIP.2003.819861. [DOI] [PubMed] [Google Scholar]
  • 44.Chen A, Kurhanewicz J, Bok R, Xu D, Joun D, Zhang V, Nelson SJ, Hurd RE, Vigneron DB. Feasibility of using hyperpolarized [1-13C]lactate as a substrate for in vivo metabolic 13C MRSI studies. Magn. Reson. Imag. 2009;26:721–726. doi: 10.1016/j.mri.2008.01.002.Feasibility. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 45.Schroeder MA, Atherton HJ, Ball DR, Cole MA, Heather LC, Griffin JL, Clarke K, Radda GK, Tyler DJ. Real-time assessment of Krebs cycle metabolism using hyperpolarized 13C magnetic resonance spectroscopy. FASEB J. 2009;23:2529–2538. doi: 10.1096/fj.09-129171. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 46.Chen HY, Larson PEZ, Bok RA, Von Morze C, Sriram R, Santos RD, Santos JD, Gordon JW, Bahrami N, Ferrone M, Kurhanewicz J, Vigneron DB. Assessing prostate cancer aggressiveness with hyperpolarized dual-agent 3D dynamic imaging of metabolism and perfusion. Cancer Res. 2017;77:3207–3216. doi: 10.1158/0008-5472.CAN-16-2083. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 47.Von Morze C, Bok RA, Reed GD, Ardenkjaer-Larsen JH, Kurhanewicz J, Vigneron DB. Simultaneous multiagent hyperpolarized 13C perfusion imaging. Magn. Reson. Med. 2014;72:1599–1606. doi: 10.1002/mrm.25071. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 48.Feng Y, Gordon JW, Shin PJ, von Morze C, Lustig M, Larson PEZ, Ohliger MA, Carvajal L, Tropp J, Pauly JM, Vigneron DB. Development and testing of hyperpolarized 13C MR calibrationless parallel imaging. J. Magn. Reson. 2016;262:1–7. doi: 10.1016/j.jmr.2015.10.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 49.Ong F, Lustig M. Beyond low rank + sparse: multiscale low rank matrix decomposition. IEEE J. Sel. Top. Signal Process. 2016;10:672–687. doi: 10.1109/JSTSP.2016.2545518. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 50.Doneva M, Börnert P, Eggers H, Stehning C, Sénégas J, Mertins A. Compressed sensing reconstruction for magnetic resonance parameter mapping. Magn. Reson. Med. 2010;64:1114–1120. doi: 10.1002/mrm.22483. [DOI] [PubMed] [Google Scholar]
  • 51.Tofts PS. Quantitative MRI of the Brain: Measuring Change Caused by Disease. John Wiley and Sons; Chichester, UK: 2003. [DOI] [Google Scholar]
  • 52.Mariager CØ, Nielsen PM, Qi H, Schroeder M, Bertelsen LB, Laustsen C. Can hyperpolarized 13 C-urea be used to assess glomerular filtration rate? A retrospective study. Tomography. 2017;3:146–152. doi: 10.18383/j.tom.2017.00010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 53.Milshteyn E, von Morze C, Gordon JW, Reed GD, Bok RA, Vigneron DB. A Hyperpolarized 13C MRI Approach for Calculating Glomerular Filtration Rate. Proc. Intl. Soc. Mag. Reson. Med. 25:1233. (n.d.) [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Figure S1
NIHMS963014-supplement-Figure_S1.tif (18.6MB, tif)
Video 1

Video 1. All time-points from the 2-fold accelerated 1 × 1 mm2 HP001 T2 Mapping acquisition used in the analysis (some cutoff due signal over-ranging).

Download video file (46.5KB, mov)
Video 2

Video 2. The dynamics of the urea over the course of the 3D 1 mm isotropic T2 mapping acquisition can be seen in the accompanying video. Each 360° rotation signifies one time-point, with the temporal resolution of the acquisition being 2.3 s. The signal decays rapidly outside the kidneys, and lasts the longest within the renal pelvis, which is known to have the longest T2 values.

Download video file (1.5MB, mov)
Video 3

Video 3. All time-points from the 2-fold accelerated 1 × 1 mm2 lactate T2 Mapping acquisition used in the analysis (some cutoff due signal over-ranging).

Download video file (37.9KB, mov)
Video 4

Video 4. All time-points from the 2-fold accelerated 1 × 1 mm2 C2-pyruvate T2 Mapping acquisition used in the analysis (some cutoff due signal over-ranging).

Download video file (51KB, mov)

RESOURCES