Complexidade 4 caos
- 1. Caos
- 2. Os conceitos de:Os conceitos de: Ordem x DesordemOrdem x Desordem Harmonia x CaosHarmonia x Caos Bem x MalBem x Mal PermearamPermearam e continuam permeandoe continuam permeando as culturas da Terraas culturas da Terra
- 3. No Hinduísmo o Cosmo passa por 3 fases: Criação (Brahma) Conservação (Vishnu) Destruição (Shiva)
- 4. Contudo Vishni e Shiva não representam o bem e o mal, são apenas duas manifestações diferentes de Brahma Benevolência x Fúria Harmonia x Discórdia
- 5. Conservação (Vishnu) ⇒ Ordem Destruição (Shiva) ⇒ Caos Ordem e Caos são manifestações diferentes de um determinismo subjacente (Brahma) Não existem isolados A Ciência mostra que a Natureza é infatigavelmente não linear
- 6. Até meados do século XX acreditava-se que a Natureza era linear. Mesmo após se verificar a não linearidade da maioria dos fenômenos naturais, a modelagem matemática concentrou-se em montar equações lineares dos fenômenos, só porque estas equações eram solúveis...
- 7. O que é Caos? A palavra caos sempre teve, na mente das pessoas, uma conotação negativa.
- 8. Sempre esteve associada a destruição e desordem.
- 9. Visto como a contraposição de ordem e de criação Oposto à emergência
- 10. Essa visão dicotômica de caos x criação é uma herança da cultura ocidental greco-romana-judaico-cristã-muçulmana, que coloca tudo em termos antagônicos: bem x mal frio x calor criação x destruição
- 11. Essa visão não é compartilhada por muitas culturas orientais. Na escrita chinesa, o caractere mnemônico que representa a palavra crise é uma combinação dos caracteres de perigo e oportunidade. Perigo – 危險 Oportunidade – 機會 Crise – 危機
- 12. Nessa cultura, uma crise é um período de grande perigo, desordem e caos; mas contém dentro de si um embrião de uma oportunidade, criar uma nova realidade, fazer tudo de uma forma nova. A crise destrói a antiga ordem, abrindo espaço para que uma nova ordem surja.
- 13. Caos – conceito matemático: Comportamento estocástico que ocorre num sistema determinístico
- 14. Sistemas Previsíveis Pêndulos Sistema massa-mola e Não- Previsíveis Clima Fluidos turbulentos
- 15. As equações de Newton, que regem a mecânica, são determinísticas: Dadas as forças agindo sobre um sistema de partículas e as condições iniciais somos capazes de determinar o movimento do sistema.
- 16. Mas se atirarmos bolinhas para cima aproximadamente do mesmo modo, porque elas não caem aproximadamente no mesmo lugar?
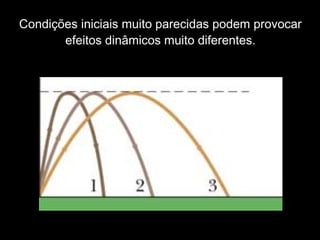
- 17. Condições iniciais muito parecidas podem provocar efeitos dinâmicos muito diferentes.
- 18. Sistemas muito simples podem ter comportamentos complexos, onde pequenas diferenças iniciais são amplificadas, levando a um comportamento aleatório.
- 20. Henri Poincarè em 1880 pesquisou os problemas relacionados à impossibilidade de resolução das equações diferenciais não lineares, na busca das leis da uniformidade e da unificação dos sistemas físicos. Seu objetivo era descrever o que ocorreria matematicamente quando se introduzia num sistema gravitacional uma massa complementar num sistema duplo, isto é, passando a análise de dois para três corpos gravitacionais interagindo mutuamente. Acabou descobrindo que os sistemas de massas gravitacionais com 3 corpos evoluíam sempre para um equilíbrio irregular. As órbitas tendiam a não ser periódicas, tornavam-se complexas e irregulares.
- 21. Poincaré descobriu que ao invés de existirem órbitas ordenadas, equilibradas e regulares, ou um sistema equilibrado e harmônico, o que ocorriam eram sistemas verdadeiramente desestabilizados, onde o que prevaleceria não era a ordem natural, e sim o caos, a confusão, pois os movimentos se tornavam aleatórios.
- 22. Henri Poincaré
- 23. Os resultados observados que levavam à confusão e à desarmonia, não condiziam com a harmonia que ocorria na mecânica clássica. Poincaré neste seu trabalho acabou por descobrir uma possibilidade da existência de um sistema desordenado, com variáveis ao acaso. Na época não houve um interesse prático na sua teoria de órbitas irregulares, sendo muitas vezes considerada a teoria uma aberração matemática. Continuaram havendo alguns estudos esparsos por outros matemáticos, porém como curiosidade sobre os Sistemas dinâmicos não-lineares.
- 24. Quanto mais negativo é o expoente de Lyapunov, mas rápido a série converge para os valores finais, quando o expoente é positivo, o sistema apresenta comportamento caótico Aleksandr Mikhailovich Lyapunov
- 25. Suas principais preocupações eram a estabilidade dos equilíbrios eo movimento de sistemas mecânicos, a teoria do modelo para a estabilidade do líquido turbulento uniforme, eo estudo de partículas sob a influência da gravidade. Seu trabalho no campo da física matemática considerado o problema do valor limite da equação de Laplace. Na teoria do potencial, a sua obra de 1897 sobre algumas questões relacionadas com Dirichlet do problema esclareceu vários aspectos importantes da teoria. Seu trabalho neste campo é, em estreita ligação com o trabalho de Steklov. Lyapunov desenvolvido muitos métodos de aproximação importantes. Seus métodos, que ele desenvolveu em 1899, tornam possível
- 26. Edward Lorenz na década de 60 tentava resolver equações matemáticas para previsão do tempo com computadores.
- 27. O tempo de processamento era longo, e as vezes, ele interrompia os cálculos, para continuar mais tarde.
- 28. O computador imprimia o último valor, para cada uma das variáveis, valores que ele reintroduzia no programa, quando continuava a calcular. Por exemplo: 3.701502 → impresso
- 29. Contudo, para seu espanto, cada vez que ele fazia isso, os resultados obtidos eram totalmente diferentes daqueles caso não interrompesse o programa.
- 30. Por exemplo: Quando o computador caculava direto o resultado final era: 8,987734 Quando o computador parava no meio dos cálculos e imprimia o valor intermediário da variável, 3.701502, e este era reintroduzido, o resultado final, se tornava: 0,032701
- 32. O que o computador imprimia para cada uma das variáveis, era um valor arredondado. Por exemplo: 3.701502 → impresso 3.701502432 → na memória A diferença nos 3 últimos algarismos levava a uma divergência, nos cálculos, que crescia com o tempo.
- 33. Preto: x(0)=0.480 v(0)=0.355 Vermelho: x(0)=0.481 v(0)=0.355 Verde: x(0)=0.482 v(0)=0.355 O cálculo é tão complicado que o resultado torna-se imprevisível após algum tempo Condições iniciais
- 34. Essas descobertas ficaram desconhecidas do restantes dos cientistas por mais de 10 anos. A publicação do artigo, que deu origem a toda uma nova área da matemática, havia sido publicada na “Gazeta do Estrangulador de Bodes” (Journal of Atmospheric Sciences) Isto é, um jornal científico, que ninguém lia.
- 35. Caos = sensibilidade às condições iniciais Condições iniciais muito próximas separam-se exponencialmente rápido ⇒ Efeito Borboleta Existe um tempo característico τ dentro do qual previsões são possíveis. Além desse tempo o sistema torna-se imprevisível. O fator 1/τ é chamado de expoente de Lyapunov (é uma freqüência).
- 36. Exemplo 1: 1 0n n nx x x+ = ≥ x0 = 49.0 x0 = 0.030 x0 = 1 x0 = 0 x1 = 7.0 x1 = 0.173... x1 = 1 x1 = 0 x2 = 2.646... x2 = 0.416... x2 = 1 x2 = 0 x3 = 1.627... x3 = 0.645... x3 = 1 x3 = 0 x4 = 1.275... x4 = 0.803... x4 = 1 x4 = 0 x5 = 1.129... x5 = 0.896... x5 = 1 x5 = 0 x6 = 1.063... x6 = 0.947... x6 = 1 x6 = 0 x7 = 1.031... x7 = 0.973... x7 = 1 x7 = 0 0 1 Ponto fixo instável Ponto fixo estável 1>x>0x>1 X=1 X=0
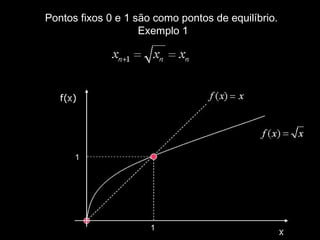
- 37. Pontos fixos 0 e 1 são como pontos de equilíbrio. Exemplo 1 1 1
- 38. x0 = 0.030 x1 = 0.173... x2 = 0.416... x3 = 0.645... x4 = 0.803... x5 = 0.896... x6 = 0.947... x7 = 0.973... 1 1 Partindo de x0; x1 será a raiz quadrada de x0 e assim por diante
- 39. Resumindo Extraindo a raiz de um número, depois a raiz deste e assim por diante, chegamos a um número limite, no nosso exemplo é o número 1.
- 40. Exemplo 2: 2 1 0n n nx x x+ = ≥ x0 = 2.0 x0 = 0.8 x0 = 1 x0 = 0 x1 = 4.0 x1 = 0.64 x1 = 1 x1 = 0 x2 = 16 x2 = 0.4096 x2 = 1 x2 = 0 x3 = 256 x3 = 0.1677... x3 = 1 x3 = 0 x4 = 65536 x4 = 0.0281... x4 = 1 x4 = 0 x5 = 4294967296 x5 = 0.0008... x5 = 1 x5 = 0 0 1 Ponto fixo instável Ponto fixo estável 1>x>0x>1 X=1 X=0
- 41. x x0 = 2.0 x1 = 4.0 x2 = 16 x3 = 256 x4 = 65536 x5 = 4294967296 O pontos fixos 0 e 1 não são pontos de equilíbrio. Exemplo 2. f(x) 2 4
- 42. Resumindo Encontrando o quadrado de um número, depois o quadrado deste e assim por diante, não chegamos a um número limite, a seqüência diverge para o ∞.
- 43. Curiosidade Para descrever o crescimento de uma população de coelhos Fibonacci em 1220, criou uma seqüência de numérica, que descrevem o número de casais numa população de coelhos depois de n meses supondo que:
- 44. no primeiro mês nasce apenas um casal, casais reproduzem-se já no segundo mês de vida, não há problemas genéticos no cruzamento consangüíneo, todos os meses, cada casal fértil dá a luz a um novo casal, e os coelhos nunca morrem.
- 45. Em 114 gerações o volume de coelhos seria maior que o do universo conhecido e antes disso a Terra seria envolvida por uma esfera de coelhos, que se expandiria a velocidade maior do que a da luz.
- 46. Mas em um ciclo como este não existe, pois onde existe a necessidade de alimento e os predadores, isso não acontece. Muitos coelhos Raposas produzindo mais filhotes Mais raposas Menos coelhos Menos raposas
- 47. Exemplo 3: Mapa logístico Seja Xn a população de insetos uma determinada espécie na geração n. A cada geração uma parte da população morre e filhotes nascem. O número de indivíduos na geração seguinte é aproximadamente proporcional ao número de indivíduos na geração anterior: Xn+1 = µ Xn
- 48. Se µ < 1 a população decresce Se µ > 1 a população cresce Se a população fica muito grande pode faltar comida, então a taxa de crescimento não pode ser constante. Substituímos µ por: µ(1-Xn/Xc) onde Xc é o maior número de indivíduos que pode sobreviver com os recursos existentes.
- 49. Observe que (1 / ) 0 n c n c n c se X X X X se X X µ µ << − ≈ ≈ Então a equação que descreve a população fica: 1 (1 / )n n n cX X X Xµ+ = − 1 (1 )n n nx x xµ+ = − 1 (1 )n n n c c c X X X X X X µ+ = − Dividindo os dois lados por Xc e definindo uma nova variável xn = Xn/Xc xn é a fração da população máxima que sobrevive
- 50. Gráficos de x contra n, onde: x – fração da população sobrevivente n – nº de gerações µ – taxa de crescimento
- 51. 1 (1 ) 0 1 2.7n n n nx x x xµ µ+ = − ≥ ≥ = x0 = 0.5 x1 = 0.675 x2 = 0.597... x3 = 0.650... x4 = 0.615... x5 = 0.640... x6 = 0.622... x7 = 0.634... Xn = 0.629... Pontos fixos: xn+1 = xn Soluções: x=0 e x = (µ−1)/µ = 0.629... Após alguma oscilação inicial a fração da população sobrevivente estabiliza em 0,629
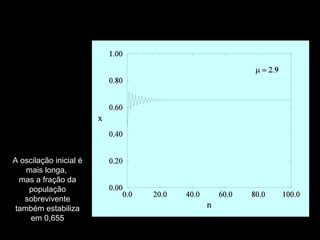
- 52. A oscilação inicial é mais longa, mas a fração da população sobrevivente também estabiliza em 0,655
- 53. Não ocorre mais estabilização, apenas oscilações regulares
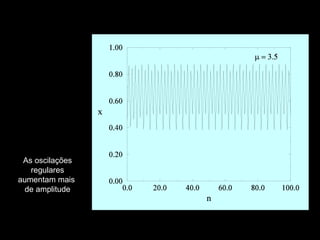
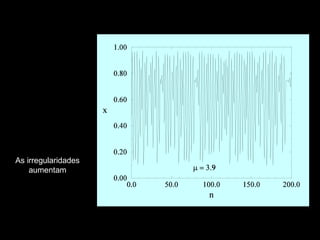
- 55. As oscilações regulares aumentam mais de amplitude
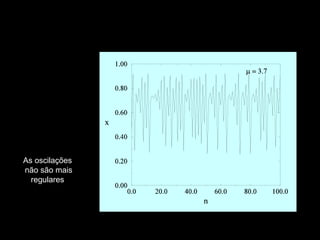
- 56. As oscilações não são mais regulares
- 58. Gráficos de x contra µ onde: x – fração da população sobrevivente µ – taxa de crescimento
- 59. Rota para o caos por duplicação de período (Taxa de crescimento) (Fraçãodapopulação)
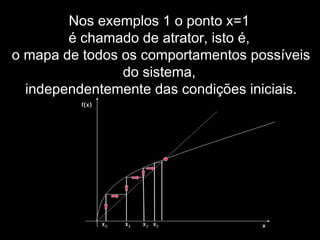
- 63. Nos exemplos 1 o ponto x=1 é chamado de atrator, isto é, o mapa de todos os comportamentos possíveis do sistema, independentemente das condições iniciais.
- 64. Nos exemplos 2 não existe atrator. O comportamento do sistema diverge para o infinito.
- 65. Mas no caso do exemplo 3 (mapa logístico - crescimento populacional), que leva ao caos, o atrator não é um ponto ou uma curva fechada, mas uma curva complexa, muitas vezes um fractal.
- 66. Rota para o caos por duplicação de período No diagrama os ramos vão se bifurcando, por fim esses pontos de crise (bifurcações), acabam ocorrendo com tanta freqüência que se superpõe, formando um denso aglomerado de possibilidades.
- 67. Entre a1 e a4, na região de crise (bifurcação), existem opções limitadas 50% por vez Em a∞, o nº e de possibilidades não aumentam infinitamente, mas ocorrem regiões de regularidades, dentro do caos, e nessas regiões de regularidade regiões mais de caos, ad infinitum... Nessas superposições é oferecida uma fantástica amplitude de comportamentos devido ao número enorme de possíveis estados possíveis. O sistema já não está mais confinado a um número limitado de ramos, é livre para experimentar um infinidade de possibilidades.
- 68. No estudo de equações do comportamento do clima, Lorenz gerou, o hoje chamado atrator de Lorenz, que é, o mapa do estado da atmosfera com qualquer condição inicial. (Para aquelas equações do clima)
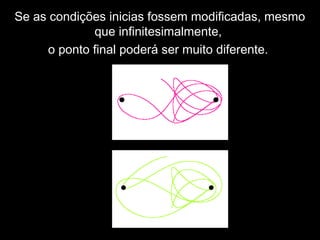
- 69. Se as condições inicias fossem modificadas, mesmo que infinitesimalmente, o ponto final poderá ser muito diferente.
- 70. Daí que vem a famosa afirmação, de que um bater de asas de uma borboleta no Japão pode gerar um furacão nos EUA
- 71. Constante de Feigenbaum Um comportamento interessante é que para valores de µ maiores que 3, no nosso exemplo, ocorre uma duplicação do período de recorrência. Essa duplicação foi estudada por Armand Vallin Feigenbaum.
- 72. Ele descobriu que a duplicação ocorria na razão de 4,6692016090... Não importando qual fosse a equação da qual se partisse. As mudanças de escala (duplicação) geram um comportamento semelhante ao anterior (auto-similaridade).
- 73. A medida que fazemos mais e mais ampliações verifica-se, que a figura se estabiliza e praticamente uma é igual a outra. f(x) = a se n( x)π Renormalização f(x) = a. x(1 - x)
- 75. Renormalização Transição de fase Mudança de escala
- 76. Na perspectiva clássica lei da natureza é determinística e reversível no tempo. A noção de caos nos obriga a reconsiderar a noção de lei da natureza. Possibilidades...
- 77. CélulasCélulas (vida)(vida) seriamseriam capazes de fazercapazes de fazer suas transiçõessuas transições no intervalo entreno intervalo entre caos e ordem.caos e ordem.
- 78. Final da parte 4Final da parte 4