Complexidade 5 fractais
- 1. Fractais
- 2. O QUE SÃO FRACTAIS? 1) São conjuntos auto-similares: ampliações sucessivas do conjunto reproduzem exatamente o mesmo conjunto. ou 2) São conjuntos quase auto-similares: ampliações sucessivas parecidas com o conjunto inicial, mas não idênticas. O importante é que cada ampliação revele novas estruturas.
- 3. Características: — Auto-similaridade — Estruturas numa série infinita de escalas — Preenchem mais espaço que uma curva e menos que uma superfície — Dimensão fracionaria
- 4. Caos e fractais são primos matemáticos, a relação entre eles vem através do atrator que pode ser fractal, assim as possibilidades de acomodação do sistema podem ser “infinitas”.
- 5. Dimensão fractal Dimensão fracionária - O matemático alemão, Félix Hausdorf, deu uma das primeiras versões ao conceito de dimensão. Para ele, uma superfície plana tem duas dimensões, pois temos de multiplicar dois números para calcular sua área. Do mesmo modo, um bloco é tridimensional, pois precisamos multiplicar três números para calcular seu volume.
- 6. Hausdorf pensou que essa regra simples era suficiente para catalogar todas as figuras, desde 0-D até ∞-D. A possibilidade de fracionar o número de dimensões, foi aventada pelo matemático Benoit Mandelbrot, da IBM, em 1975. Ele concluiu que algumas figuras concebidas pelos matemáticos, no passado, não podiam ser catalogadas satisfatoriamente pela regra de Hausdorf e, baseando-se em fenômenos naturais comuns, apresentou alguns exemplos:
- 7. Imaginou calcular a área da Inglaterra, fazendo a da linha da costa, aproximadamente, um retângulo. Pela regra de Hausdorf, para calcular a área, bastava multiplicar o comprimento pela largura, mas Mandelbrot percebeu que, nesse caso, a aplicação da regra era mais complicada. Como decidir qual a unidade de medida para comprimento e largura do retângulo?
- 8. Imagine-se voando num balão suficientemente distante do retângulo para não perceber os recortes da costa. Vê-se um retângulo de 1000 km de comprimento e cerca de 130 km de largura. Assim, pode concluir que a área do retângulo é de 130.000 km2 .
- 9. Ao voltar para o solo, você perceberá o ondulado do retângulo e, ao contorná-lo em um automóvel, verificará que as melhores medidas para o comprimento e para a largura do retângulo são 1300 km e 150 km. Dessa forma, a área saltaria para 195.000 km2 . A exatidão seria ainda pior, se nos imaginássemos fazendo a viagem no dorso de um inseto. Ao percorrermos todas as pequenas reentrâncias do retângulo, iríamos calcular uma área muito maior.
- 10. O paradoxo observado por Mandelbrot é que, à medida que melhoramos as estimativas do comprimento e da largura, pioramos o cálculo da área. Mandelbrot percebeu que alguns objetos geométricos, teriam sua área calculada, não pelo produto de dois números, mas, pelo produto de um número pela raiz quadrada de outro número. Isso equivale a dizer que a Inglaterra é um objeto de dimensão 1,5. Estava criada a dimensão fracionária.
- 12. A Curva de Koch e o Floco de Neve D=1,26
- 13. Triângulo de Sierpinski – D=1,58
- 14. Esponja de Menger – D=2,73
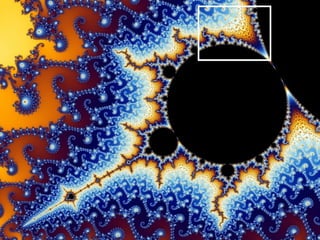
- 15. UM EXEMPLO DE FRACTAL QUASE AUTO- SIMILAR: O CONJUNTO DE MANDELBROT
- 30. Conjunto de Mandelbrot animação
- 32. Outros Objetos fractaisOutros Objetos fractais
- 57. Final da parte 5Final da parte 5