Medidas de dispersão AULA 1 EXPERIMENTACAO.pptx
- 1. Medidas de dispersão; exemplos práticos de aplicação Prof. Dra.: Patrícia Ferreira da Silva patrycyafs@yahoo.com.br
- 2. • Efeitos de Fatores não Controlados Variação ao Acaso ou aleatórias Por que usamos estatística?
- 3. Circularidade do Método Científico Validade das Conclusões PLANEJAMENTO (1) FORMULAÇÃO DE HIPÓTESES (2) OBSERVAÇÕES (3) TESTES DAS HIPÓTESES FORMULADAS ANÁLISE ESTATÍSTICA (4) DESENVOLVIMENTO DA TEORIA
- 4. Medidas de posição ou Tendência central • Representa o valor em torno do qual os dados observados tendem a se acumular.
- 5. Média Aritmética • Consiste na soma de todas as observações, dividida pelo número delas. 𝑋 = 𝑋𝑖 𝑛 𝑋 = 𝑚é𝑑𝑖𝑎; Xi = valor observado; N= número de observações
- 6. Mediana • Conjunto de dados ordenados (rol) é o valor que divide esse conjunto em dois subconjuntos com igual número de dados 𝑚𝑑 = (𝑋𝑘+𝑋𝑘+1) 2 • Se for um conjunto par • Se for um conjunto impar A mediana é o valor que está no centro da sequência.
- 7. Moda • No conjunto de dados é o valor que ocorre com maior frequência. • Pode ter mis de uma moda em um conjunto de dados indicando heterogeneidade
- 9. O que vem a ser a Dispersão? • Dispersão ou variação consiste no grau com que os dados tendem a se afastar de um valor central, geralmente a média aritmética.
- 10. Amplitude (R - range) •Diferença entre o maior e o menor valor do conjunto de dados. •Ignora como os dados estão distribuídos. 𝐴𝑚𝑝𝑙𝑖𝑡𝑢𝑑𝑒 = 𝑋𝑖 𝑚á𝑥𝑖𝑚𝑜 − 𝑋𝑖 𝑚í𝑛𝑖𝑚𝑜
- 11. Variância população • Variância pode ser definida como: "a média dos quadrados dos desvios em relação à média aritmética”. •“O quão longe" os valores se encontram da média. 𝜎2 = 𝑋𝑖 − 𝑋 2 𝑛 SQD = soma de quadrado de desvio 𝜎2 = 𝑖=1 𝑛 𝑋𝑖2 − 𝑋𝑖 2 𝑛 𝑛
- 12. Variância Amostra •A variância é sempre um valor positivo, e sua unidade é quadrática.. 𝑠2 = 𝑆𝑄𝐷 𝑁 = 𝑖=1 𝑛 𝑋2 − 𝑖=1 𝑛 𝑋𝑖 2 𝑛 𝑛 − 1 GL= grau de liberdade
- 13. Desvio Padrão •É a raiz quadrada da variância, tomada como valor positivo. •É a mais utilizada das medidas de dispersão. σ = 𝜎2 𝑠 = 𝑠2 𝑠 = 𝑄𝑀𝑅
- 14. Coeficiente de Variação •Relaciona o desvio padrão em termos de porcentagem da média aritmética. C𝑉 = 𝜎 𝑋 ∗ 100 C𝑉 = 𝑠 𝑋 ∗ 100 Bom Regular Duvidoso 0 ≤ CV% < 10 10 ≤ CV% < 20 20 > CV% CV% = 𝑄𝑀𝑅 𝑀𝑔 *100
- 15. Erro Padrão da Média •Dá uma ideia da precisão com que foi estimada a média da amostra. •Quanto menor for o erro padrão da média, melhor será a estimativa da média da amostra. 𝑠 𝑋 = 𝑠 𝑛
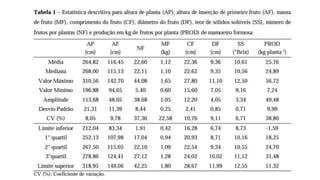
- 16. Exemplo Prático 49,2 31,1 12,4 22,6 66,6 31,9 21,5 29,1 19,8 24,5 24,4 23,3 24,4 26,7 14,7 57,2 25,5 39,4 29,7 23,3 30,9 33,3 52,7 31,7 36,2 30,6 24,0 33,8 35,4 38,7 Com base nos dados de altura de plantas de tomate cereja, variedade com crescimento indeterminado, determine a média; mediana; moda; desvio padrão, variância e coeficiente de variação.
- 19. Os valores negativos, observados, são devido as outliers, ou seja, indicam possíveis valores discrepantes, em decorrência dos valores estarem abaixo ou acima do limite de detecção de outliers. Esse limite é determinado por meio do intervalo interquartílico, dado pela distância entre o primeiro e o terceiro quartil, assim o limite inferior é determinado da seguinte forma: limite inferior = Primeiro Quartil – 1,5 * (Terceiro Quartil – Primeiro Quartil). Pode-se dizer desta forma que quando a linha da mediana está próxima ao primeiro quartil, os dados são assimétricos positivos e quando a posição da linha da mediana é próxima ao terceiro quartil, os dados são assimétricos negativos.