Precificação de ativos de risco

Finanças Aplicadas I
Felipe Pontes
Precificação de ativos de risco
Objetivo: após essa aula o aluno deverá
compreender o funcionamento e as
aplicações do CAPM padrão.

• Relembrando, o retorno BNHR é dado por:
• Dividendos (D) e Preço (P) são anualizados, o
que segundo Guerard e Schwartz (2007) é
arbitrário, mas amplamente utilizado em
finanças.
Retorno Buy and Hold (BNHR)
2

Retorno Buy and Hold (BNHR)
• O Banco do Brasil (BBAS3) pagou dividendos e
JSCP em 2013 conforme a planilha abaixo,
onde também é informado o preço do início e
do final do ano. Calcule o retorno sem
considerar o valor do dinheiro no tempo.
3
Data
Dividendo
(R$)
JSCP
(R$)
Preço t-1
(R$)
Preço t
(R$)
30/12/13 - - - 24,25
27/08/13 - 0,31 - -
06/08/13 0,77 - - -
28/05/13 - 0,28 - -
14/05/13 0,10 - - -
26/02/13 - 0,26 - -
19/02/13 0,26 - - -
28/12/12 - - 23,24 -

Single-index Model
• O CAPM surgiu da necessidade de se analisar
as relações entre risco e retorno de forma
menos “custosa” e tudo começou com o
Single-index model (de SHARPE, 1963):
1. Em 1961 o melhor computador da época
necessitava de 33 minutos para otimizar uma
carteira de 100 ativos, ao custo de U$ 300,00,
inviabilizando testes e simulações (hoje temos o
Solver, no Excel);
2. Em média as IFs seguem 200 ativos (ELTON;
GRUBER, 1995). Pela teoria de Markowitz é
necessário calcular 200 E(Ri) e Var, além de
(N*(N-1)/2) Correlações. 4

Single-index Model
• O pressuposto de Markowitz era de que os
ativos estavam correlacionados entre si. O de
Sharpe é que eles estavam correlacionados
com um Single-index e indiretamente entre si.
• O que é o single-index e por que os ativos
estariam correlacionados com ele?
• Analisemos o comportamento das ações no
próximo slide.
5

Single-index Model
6
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1 2 3 4 5 6 7 8 9 10 11 12 13
Series1
Series2
Series3
Series4
Ver na planilha com algumas ações individualmente

Single-index Model
• O retorno de uma ação deve ser dado por:
• Como isso funciona com uma carteira (que é
teoricamente bem diversificada),
especialmente com relação ao “ai“?
7
Componente do
retorno que é
independente
do “mercado”
Sensibilidade
da ação em
relação ao
mercado
Retorno do
mercado

Single-index Model
• O “ai” pode ser segregado em duas partes (o
valor esperado e a incerteza, com esperança
igual a ZERO):
• Reescrevendo o single-index:
• Os parâmetros desse modelo são estimados
por série temporal (faremos mais na frente).
8

Single-index Model
• Pressupostos do modelo:
1.
2. O erro de um ativo é independente de qualquer
outro ativo para qualquer valor.
3. O erro da regressão tem valor esperado igual a
zero.
• Com isso, apenas o co-movimento com o
mercado faz com que as ações variem juntas.
9

Single-index Model
• Sharpe (1963) derivou a partir desses
pressupostos as três equações fundamentais
do seu modelo:
1. Retorno esperado:
2. Variância do ativo:
3. Covariância entre os ativos:
10

Single-index Model
• Retorno esperado da carteira:
• Variância da carteira:
11

O βeta
• A definição matemática do β é:
• Qual é o β de uma carteira formada por todos
os ativos do mercado?
12

O βeta
• Calcule o beta da ação da Jelco (retirado de
Ross, Westerfield e Jaffe, 2002)
13

O βeta
• Ver o seguinte vídeo:
http://www.investopedia.com/video/play/und
erstanding-beta/
14

Questões conceituais
1. Se todos os investidores tiverem expectativas
homogêneas, que carteira de ativos de risco
possuirão?
2. Por que o Beta é uma medida apropriada de
risco de um título numa carteira ampla?
15

Estimação do beta
• Na prática, estima-se o b pelo modelo de
mercado (single-index).
• Período para estimativa (GUERARD,
SCHWARTZ, 2007):
– Geralmente 5 anos, com retornos mensais – com
60 observações (padrão do Economatica®);
– Embora pode-se utilizar qualquer número de
observações;
– Cuidado apenas com os pressupostos da
regressão.
16

Estimação do beta
• A carteira de mercado:
– É uma carteira teórica que inclui todos os tipos de
ativos do mercado financeiro, ponderada pela
participação de cada ativo no mercado.
– Se todo o mercado for composto pelos ativos A, B
e C, com capitalização respectiva de $ 1, $ 2 e $ 7.
A participação de cada ativo na carteira de
mercado será respectivamente de 10%, 20% e
70%.
• Representação prática:
– Um índice de ativos que representem o
“mercado” (S&P500, DJIA, Ibovespa etc.). 17

Estimação do beta
• Estimar o b com base nessa planilha.
• Usar o modelo de mercado:
Rt – Rft = at + bt(Rmt – Rft) + et
18

Estimação do beta
• O passo a passo para a estimação usando o
GRETL pode ser encontrado nos vídeos abaixo:
• Português: https://youtu.be/h0aEUt7caMY
• Espanhol: https://youtu.be/M1FW0wXDbdw
19

Estimação do beta
• Passos básicos no GRETL (nos limitaremos a discutir
conceitos de Finanças):
1. Inserindo a planilha: File  Open data  User File
(lembre de escolher a opção “All Files”, pois o arquivo
está em Excel)  selecione a planilha  Sheet to
import  “dados ajustados sem fórmula”.
2. Definindo o modelo: Model  Ordinary Least
Squares  Insira as variáveis no modelo  clique OK.
3. Testes de pressupostos: Tests  escolher um de cada
vez (“Normality of residuals”, “Autocorrelation”, é
interessante também avaliar se há quebra estrutural
no modelo com os “CUSUM”s – podendo gerar algum
problema).
4. Não discutiremos aqui estacionaridade das séries.
20

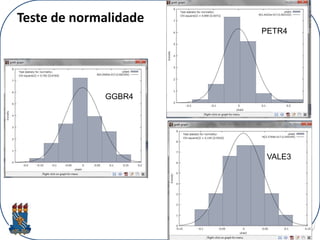
21
Os testes dos pressupostos foram realizados para
todas as ações: os resíduos apresentaram-se
normalmente distribuídos e não houve evidência
de autocorrelação serial para nenhum dos três
casos.

Sensibilidade
• Qual das 3 ações é mais sensível às variações
da carteira de mercado?
24

Teste de normalidade
25
PETR4
VALE3
GGBR4

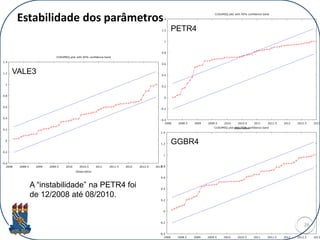
Estabilidade dos parâmetros
26
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
1.2
1.4
2008 2008.5 2009 2009.5 2010 2010.5 2011 2011.5 2012 2012.5 2013
Observation
CUSUMSQ plot with 95% confidence band
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
1.2
1.4
2008 2008.5 2009 2009.5 2010 2010.5 2011 2011.5 2012 2012.5 2013
Observation
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
1.2
1.4
2008 2008.5 2009 2009.5 2010 2010.5 2011 2011.5 2012 2012.5 2013
PETR4
VALE3
GGBR4
A “instabilidade” na PETR4 foi
de 12/2008 até 08/2010.

Risco-Retorno no CAPM
• O modelo proposto, de forma independente,
por Sharpe (1964), Lintner (1965) e Mossin
(1966) equilibra o retorno esperado do ativo
com uma taxa livre de risco e um prêmio pelo
risco:
• O que é a Rf?
• O que dizer sobre o β? Pense atribuindo
valores (1, maior que 1, menor que 1 e 0).
27

Problema com a taxa livre de risco (Rf):
• Black (1972) diz que é um pressuposto do
CAPM que a Rf seja menor que o Rm. Isso gera
alguns problemas, por exemplo, na utilização
do CAPM no Brasil.
• No nosso exemplo eu utilizei, arbitrariamente,
uma Rf de 5% em todos os períodos. Muitas
vezes a Rf foi maior do que o Rm. Confira na
planilha.
28

• Geralmente utilizam-se os valores esperados
das taxas de que são usadas no CAPM. Veja o
exemplo de Ross, Westerfield e Jaffe (2002):
Entre 1929 e 1999 o retorno esperado das ações
foi de 13,3% e a taxa livre de risco média foi
de 3,8% no mesmo período. Qual é o prêmio
pelo risco nesse período?
29

• No exemplo anterior foi visto que 13,3% é o
retorno esperado do mercado como um todo.
Para saber o retorno esperado de um ativo
específico basta usar o CAPM. Sabendo que a
Rf é de 3,8% calcule o retorno esperado
quando:
a) β = 0
b) β = 1
c) β = 1,4
Tire suas próprias conclusões sobre a relação
risco-retorno no CAPM.
30

31Retirado de Ross, Westerfield e Jaffe (2002)
Carteira de mercado

• Use o beta estimado pela regressão da
Petrobrás e da Gerdal para estimar o retorno
esperado no investimento dessas duas
empresas. Considere as seguintes taxas
esperadas: Rf = 3,8% e Rm =13,3%.
32

• Considere agora uma carteira formada por
50% do ativo A e 50% do ativo B, com retorno
esperado e beta, respectivamente de 21,25%,
13,65%, 1,5 e 0,7. A Rf = 7% e o prêmio pelo
risco do mercado = 9,5%. Qual é o retorno
esperado da carteira pelo CAPM?
• Agora calcule apenas o retorno esperado dos
ativos, sem o uso do CAPM. Tire suas
conclusões; 33

Anúncios, surpresas e retornos
esperados
Retorno totali = E(Ri) + Retorno Inesperadoi
• Qual é o impacto da valorização do R$ em
relação ao US$ no valor de mercado de uma
empresa brasileira que exporta tecnologia?
– A valorização já havia sido projetada pelo
mercado? De quanto foi o desvio? Depende de
vários fatores!
• Lembre-se de que o “preço desconta tudo”. A
informação só será precificada se for novidade
para o mercado: inesperada!
34

• Em value relevance existe uma linha de
pesquisa chamada de earnings surprises.
Anúncio = Parte esperada + Supresa
• Exemplo:
– qual é o efeito de um lucro surpresa?
– Qual é o efeito de um prejuízo que, em parte era
esperado, porém há uma parte inesperada?
– Qual é o efeito de um prejuízo que já era esperado
há 3 meses?
35
Anúncios, surpresas e retornos
esperados

Os pressupostos subjacentes ao
CAPM padrão
• Elton e Gruber (1995) dizem que, assim como
os físicos constroem modelos sobre o
movimento da matéria em um ambiente sem
atrito, os economistas constroem modelos
onde não consideram atritos institucionais no
movimento das ações.
• Os pressupostos são “simplificações” da
realidade para que o modelo possa ser
testado.
36

CAPM padrão
1. Não existem custos de transação (Elton e
Gruber dizem que não valeria a pena
aumentar a complexidade do modelo);
2. Os ativos são infinitamente divisíveis;
3. Ausência de taxação específica sobre a
renda:
4. Um investidor não pode mover o mercado
(o que dizer de Warren Buffet?);
37
Quer dizer que, por exemplo, tanto faz receber dividendos ou ganho de capital. Na
prática existe sim essa diferença.

CAPM padrão
5. Os investidores tomam decisões com base na
teoria das carteiras;
6. É aceitável a venda a descoberto ilimitada;
7. Existe crédito e o investidor pode emprestar
ilimitadamente à taxa sem risco;
8. Todos os ativos são comercializáveis (e o
problema de liquidez no Brasil? eg);
9. Existem expectativas homogêneas.
38

A crítica de Roll (1977)
• A crítica está relacionada às proxies utilizadas
para a carteira de mercado. E.g. por que o
capital humano não está na carteira de
mercado?
• Como usamos proxies (criticáveis) da carteira
de mercado nós não aprendemos nada sobre
o CAPM (ROLL, 1977).
39

Exercícios
• Para entregar na próxima aula:
– Por que a SML é uma linha reta?
– Quais são as diferenças entre a linha de mercado de
capitais e SML?
– O beta está morto? Justifique com base no texto da página
238.
• Fazer agora (se não der tempo, entregar na próxima
aula):
– 10.24
– 10.26
– 10.28
– 10.30
– 10.31
– 10.32
– 10.39
40

Exercício
• Faz sentido, economicamente, um beta
negativo? Justifique sua resposta com base no
texto abaixo:
http://aswathdamodaran.blogspot.com.br/2009
/02/can-betas-be-negative-and-other-well.html
41

REFERÊNCIAS
• ELTON, Edwin J. et al. Moderna teoria das
carteiras e análise de investimentos. 8ed. Rio
de Janeiro: Elsevier, 2012.
• GUERARD JR, J.B.; SCHWARTZ, E. Quantitative
Corporate Finance. New York: Springer, 2007.
• ROSS, Stephen A.; WESTERFIELD, Randolph
W.; JAFFE, Jeffrey F. Administração financeira:
corporate finance. 2ed. São Paulo: Atlas, 2002.
• ROSS, Stephen A. et al. Fundamentos da
administração financeira. 9ed. Porto Alegre:
AMGH, 2013. 42

Precificação de ativos de risco

Mais conteúdo relacionado

Precificação de ativos de risco