(※この記事執筆後に公開された「労働時間等総合実態調査」電子データを分析したところ、この記事の主要な主張である「一般労働者の1日の労働時間は、階級わけされた法定時間外労働時間数の表に階級値をあてはめて計算したものである」との推理ははずれていたことがわかりました。記事末尾の追記をごらんください。(2018-02-24))
厚生労働省「労働時間等総合実態調査」(2013) データとされる「1日の法定時間外労働の実績 (一般労働者) (平均的な者)」の表が国会で使われている問題について。
2月9日の国会 (衆議院予算委員会) で質問した山井和則代議士 (希望の党) のツイートで当該表の写真が公開されている。
今日の予算委員会で、長妻議員、今井議員が指摘した疑惑の厚労省調査のデータ(添付)。裁量労働制のほうが一般の労働者より労働時間が短い、と安倍総理が答弁した調査では、1日に平均23時間超、働いている一般の労働者が9人もいます。おかしい。
http://twitter.com/yamanoikazunori/status/963234256439750656
-----
山井 和則 2018-02-13 10:11 のツイート
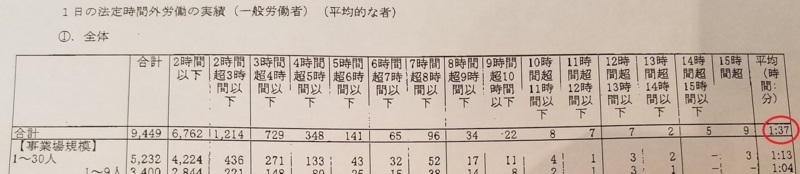
下図はこのツイートにふくまれる写真の上部を切り取ったもの。右端の「平均 (時間:分)」(赤丸部分) の値が1時間37分となっている。これに法定労働時間である8時間を足した9時間37分が一般労働者の1日の労働時間であり、裁量労働制が適用されている労働者の1日あたり労働時間9時間16分よりも短い、という根拠として持ち出された。
-----
http://twitter.com/yamanoikazunori/status/963234256439750656 から作成。赤丸は引用時に加筆したもの。
問題の所在
この「9時間37分」はいくらなんでも長すぎないか、という疑惑が指摘されている。
- 上西 充子 (2018-02-03)「なぜ首相は裁量労働制の労働者の方が一般の労働者より労働時間が短い「かのような」データに言及したのか」個人 Yahoo! ニュース https://news.yahoo.co.jp/byline/uenishimitsuko/20180203-00081208/
- 上西 充子 (2018-02-06)「裁量労働制の労働者の方が一般の労働者より労働時間が短い「かのような」答弁のデータをめぐって(続編)」https://news.yahoo.co.jp/byline/uenishimitsuko/20180206-00081326/
- 上西 充子 (2018-02-10)「裁量労働制の労働者の方が一般の労働者より労働時間が短い「かのような」答弁のデータの問題性(その3)」個人 Yahoo! ニュース https://news.yahoo.co.jp/byline/uenishimitsuko/20180210-00081457/
- 上西 充子 (2018-02-10)「裁量労働制の方が労働時間は短いかのような安倍首相の答弁。撤回は不可避だが、事務方への責任転嫁は間違い」 個人 Yahoo! ニュース https://news.yahoo.co.jp/byline/uenishimitsuko/20180210-00081478/
- 上西 充子 (2018-02-12)「裁量労働制の方が労働時間は短いかのような安倍首相の答弁は何が問題なのか(予算委員会に向けた論点整理)」 個人 Yahoo! ニュース https://news.yahoo.co.jp/byline/uenishimitsuko/20180212-00081528/
一般労働者についての9時間37分という数値は、公表された調査結果にないものであり、間違った計算式によって算出されたものであり、その計算式のもととなったデータは公表されておらず、かつ異常値と思われるものが含まれており、さらに計算された9時間16分という数値は実態とかけ離れたものであるという、幾重にも折り重なった問題を含んでいる
https://news.yahoo.co.jp/byline/uenishimitsuko/20180212-00081528/
-----
上西 充子 (2018-02-12)「裁量労働制の方が労働時間は短いかのような安倍首相の答弁は何が問題なのか(予算委員会に向けた論点整理)」 個人 Yahoo! ニュース
資料の所在
この厚生労働省「労働時間等総合実態調査」(2013) に関する資料は、2013年10月30日の 第104回労働政策審議会労働条件分科会 での配布資料 2-1 『平成25年度労働時間等総合実態調査結果』 (平成25年10月 厚生労働省労働基準局) 以外にはみあたらない。この資料には調査のくわしい方法や調査票などがないので、何をやった調査なのかはよくわからない。なお、2005年にも同名の調査がおこなわれている が、こちらも出ている情報はおなじようなものであり、調査の具体的な内容は不明である。さらに、1997, 1998, 2000, 2002 の各年にも同名の調査があった模様 だが、これらについてもいまのところよくわからない。
今回問題になっている表は、『平成25年度労働時間等総合実態調査結果』 には出てこない。今国会ではじめて出てきたものである。
「平均的な者」の法定時間外労働とは
ともかく、公表されている情報では、問題の表にある「平均的な者」の法定時間外労働という概念は、つぎのように定義されている。
「平均的な者」とは、調査対象月において最も多くの労働者が属すると思われる時間外労働時間数の層に含まれる労働者のことをいう。
http://www.mhlw.go.jp/file/05-Shingikai-12602000-Seisakutoukatsukan-Sanjikanshitsu_Roudouseisakutantou/shiryo2-1_1.pdf
-----
厚生労働省 労働基準局 (2013)『平成25年度労働時間等総合実態調査結果』 p. 7
具体的には、おそらく、適当なカテゴリーにわけた選択肢を見せて「おたくの従業員中でいちばん多くが該当するのはどれですか」のようなことをたずねたのだろう。
これは要するに、連続量を適当な階級に区切った場合にいちばん頻度の高い階級はどこか、を測定したということだ。統計学では 「最頻値」(mode) と呼ばれる種類の統計量である (ただしこの厚生労働省の調査では、後で触れるるように、階級の幅が一定でないので、最頻値を求める通常の手法ではない)。
当然、これは「平均」ではない。上記のように、定義上は「平均」ということばは使われておらず、調査の際にも、「平均的な者の法定時間外労働は何時間ですか」のように訊いたわけではないのだろうから、なぜ結果報告書において「平均的な者」などという、実態からかけはなれた名称を使ったのかは謎である。ふつうに「その事業所での最頻値」とか「最頻の階級」とか呼べばいいと思うのだが。
ともあれ、これで、問題の表の読みかたはわかる。「2時間以下」「2時間超3時間以下」「3時間超4時間以下」……のように区切った階級について「従業員中でいちばん多くが該当するのはどれか」をたずねたところ、6762の事業場が「2時間以下」、1214の事業場が「2時間超3時間以下」…… のように答えた、ということであろう。なお、調査対象事業場は11575か所だった (『平成25年度労働時間等総合実態調査結果』 p. 1) ということだが、この表には9449の事業場しか出てこない。2126事業場が欠損値になっていることになるが、その原因は不明である。
「平均」の求めかた
問題の表の右端の「平均 (時間:分)」という数値は何か? 通常、こうした表 (度数分布表) から平均値等を求めるには、各階級にそれぞれ「階級値」を割り当て、その値を使って計算する。しかし、階級値が具体的にいくつだったのかということは、問題の表には書いていないようである。というか、『平成25年度労働時間等総合実態調査結果』 にも同様の形式の表がいくつも出てくるのだが、それらにも階級値の表示はない。厚生労働省労働基準局はいったい何を考えて報告書を書いているのだろうか。
仕方がないので、適当な階級値をあてはめて計算してみることにしたのだが、これが思いのほか簡単だった。
- 「2時間以下」 → 1
- 「2時間超3時間以下」 → 2
- 「3時間超4時間以下」 → 3
- ……
のように、整数をひとつずつ増やしながらあてはめるだけ (!) でよかったのだ。
検証のための Perl スクリプトを下記に示す。
%how_many_workplace = (
'-2' => 6762 ,
'2-3' => 1214 ,
'3-4' => 729 ,
'4-5' => 348 ,
'5-6' => 141 ,
'6-7' => 65 ,
'7-8' => 96 ,
'8-9' => 34 ,
'9-10' => 22 ,
'10-11' => 8 ,
'11-12' => 7 ,
'12-13' => 7 ,
'13-14' => 2 ,
'14-15' => 5 ,
'15+' => 9 ,
);
%assigned_value = (
'-2' => 1 ,
'2-3' => 2 ,
'3-4' => 3 ,
'4-5' => 4 ,
'5-6' => 5 ,
'6-7' => 6 ,
'7-8' => 7 ,
'8-9' => 8 ,
'9-10' => 9 ,
'10-11' => 10 ,
'11-12' => 11 ,
'12-13' => 12 ,
'13-14' => 13 ,
'14-15' => 14 ,
'15+' => 15 ,
);
$case_number = 0;
$weighted_total = 0;
foreach( keys %how_many_workplace ) {
$case_number += $how_many_workplace{$_};
$weighted_total += $how_many_workplace{$_} * $assigned_value{$_};
}
print "$case_number workplaces\n" ;
print "Weighted Total: $weighted_total\n";
$mean = $weighted_total / $case_number;
print "Mean: $mean (h)\n";
$hour = int $mean;
$minute = sprintf( "%2d" , 60 * ($mean - $hour) );
print "= $hour h : $minute m\n";
このスクリプトを実行するとつぎの結果が得られる。このような階級値をあたえた場合の平均値は1時間38分ということである。問題の表にある「1:37」とほぼ同じ値になる。
9449 workplaces Weighted Total: 15478 Mean: 1.63805693724204 (h) = 1 h : 38 m
詐術のタネ
このような度数分布表では、階級値をどのようにあたえるかによって、まったくちがう「平均」の値をはじき出せる。問題の表の場合、大半の事業場 (7割以上) が、最頻の階級は「2時間以下」だと答えていた。このため、「2時間以下」階級に割り当てる値によって、平均はほとんどきまってしまう。
上記で示したように、問題の表にふくまれる平均値「1:37」の算出にあたっては、この階級には「1」を割り当てたようだ。しかし、これはこの階級を代表する値としては過大だという可能性がある。「2時間以下」の階級をさらに「1時間以下」「1時間超2時間以下」に二分した場合に、前者のほうが後者より多いかもしれない。さらに、法定時間外労働がゼロの労働者の場合には、1日の労働時間が8時間を下回るケースも多いはずだ (上西充子「裁量労働制の労働者の方が一般の労働者より労働時間が短い「かのような」答弁のデータの問題性(その3)」)。平均値に8時間を足して使うということを考えるのであれば、そのような事業場についてはマイナスの値をあたえるべきである。
とにかくこの「2時間以下」の階級に全体の7割が集中しているので、この階級にどのような値をあたえるかのインパクトは非常に大きい。この値を1時間ふやせば、「平均」の値は40分以上伸びる見当である。
それにしても、なぜここで「2時間以下」という幅の広い階級わけを採用したのだろうか。これ以外の部分については1時間刻みの階級設定になっているのに、いちばん多くの事業場が集中する部分だけが2時間幅になっている。階級幅を変化させるとしたら、大勢が集中するところは細かく刻み、少ないところは粗くするのが常識である。大勢が集中するところだけ刻みを粗くするという非常識な階級わけを採用した意図は何だろうか?
もうひとつの詐術のタネとして考えられるのは、1日あたり10時間をこえるような、おそろしく長い法定時間外残業が最頻である事業場がデータにふくまれていることだ。この点は 国会質問でも問題にされていた。問題の表をよくみると、「6時間超7時間以下」までは時間数が増えるほど事業場数が減っていくのに、「7時間超8時間未満」のところでいったん増え、そのあとまた下がっていくことがわかる。
-----
http://twitter.com/yamanoikazunori/status/963234256439750656 から作成。
グラフにしてみると、「2時間以下」が飛びぬけて多いせいでこまかいところがわかりにくいのだが、法定時間外労働7時間を境に、回答者の反応が変わっていることが読み取れる。
この分布から素直に想像できることは、おそらく、これらの事業場の担当者が、実際の労働時間についての質問だと勘違いして、1日に7時間から8時間働いている従業員がいちばん多い、などと答えたのだろうということだ。そうすると、たとえば「7時間超8時間以下」「8時間以上9時間以下」「9時間以上10時間以下」の階級に入っている事業場の大部分は誤答によるものであり、もしちゃんと設問を理解して正しく答えていれば「2時間以下」と答えたであろう、ということになる。
これらの推測に基づいて計算しなおしてみた。上記 Perl スクリプトにおいて階級値を定義していた %assigned_value をつぎのように書き換えればよい:
%assigned_value = (
'-2' => 0 , # 1日8時間程度の労働
'2-3' => 2 ,
'3-4' => 3 ,
'4-5' => 4 ,
'5-6' => 5 ,
'6-7' => 6 ,
'7-8' => 0 ,
'8-9' => 0.5 , # 1日 8.5時間程度の労働
'9-10' => 1.5 , # 1日 9.5時間程度の労働
'10-11' => 2.5 , # 1日10.5時間程度の労働
'11-12' => 3.5 , # 1日11.5時間程度の労働
'12-13' => 4.5 , # 1日12.5時間程度の労働
'13-14' => 5.5 , # 1日13.5時間程度の労働
'14-15' => 6.5 , # 1日14.5時間程度の労働
'15+' => 7.5 , # 1日15.5時間程度の労働
);
結果は46分となる。これに法定労働時間8時間を足すと8時間46分であり、政府のいう「9時間37分」よりも50分ほど短くなる。
9449 workplaces Weighted Total: 7339 Mean: 0.776695946661022 (h) = 0 h : 46 m
追記 [2018-02-24]
この記事執筆後の2月19日、「働き方改革虚偽データ疑惑」野党6党合同ヒアリングにおいて、厚生労働省から「労働時間等総合実態調査」電子データが提供されました。このデータを入手して検討したところ、分の単位で記載された法定時間外労働のデータから直接計算することで、問題の平均値をふくめて表の数値が再現できることがわかりました。したがって、この記事での推理は、結果としてはずれていたことになります。この記事は、調査についての詳細がほとんど不明の状態で入手可能な資料からどのような根拠で推理を展開したかという記録としてのこしておきますが、内容についてはまちがっていたものとお考えください。
提供された電子データがどのようなものか、何が読み取れるかについては 2月24日の記事「裁量労働制と長時間労働」 をごらんください。