Location via proxy:   [ UP ]  
[Report a bug]   [Manage cookies]                
Jump to content

Fraktali

Nga Wikipedia, enciklopedia e lirë
Bashkësia Mandelbrot e vendosur në ishuj
Bashkësia Mandelbrot : kufiri i saj është një kurbë fraktale me dimensionin Hausdorff 2. (Vini re se pjesët me ngjyra të imazhit nuk janë në të vërtetë pjesë e bashkësisë Mandelbrot, por ato bazohen në atë se sa shpejt ndryshon funksioni që e prodhon atë.)
Zmadhim në kufirin e grupit Mandelbrot

Në matematikë, një fraktal është një formë gjeometrike që përmban strukturë të hollësishme në shkallë arbitrarisht të vogla, që zakonisht kanë një dimension fraktal që tejkalon rreptësisht dimensionin topologjik . Shumë fraktale duken të ngjashme në shkallë të ndryshme, siç ilustrohet në zmadhimet e njëpasnjëshme të bashkësisë Mandelbrot . [1] [2] [3] [4] Kjo ekspozitë e modeleve të ngjashme në shkallë gjithnjë e më të vogla quhet vetëngjashmëri, e njohur gjithashtu si simetri në zgjerim ose simetri e shpalosur; nëse ky përsëritje është saktësisht i njëjtë në çdo shkallë, si në sfungjerin Menger, forma quhet afine e vetëngjashme. [5] Gjeometria fraktale shtrihet në degën matematikore të teorisë së masës .

Një mënyrë që fraktalet janë të ndryshëm nga figurat gjeometrike të fundme është se si ato shkallëzohen . Dyfishimi i gjatësisë së skajit të një shumëkëndëshi të mbushur e katërfishon sipërfaqen e tij, që është dy (raporti i gjatësisë së anës së re me të vjetër) i ngritur në fuqinë e dy (dimensioni konvencional i shumëkëndëshit të mbushur). Po kështu, nëse rrezja e një sfere të mbushur dyfishohet, vëllimi i saj shkallëzohet me tetë, që është dy (raporti i rrezes së re me atë të vjetër) me fuqinë e tre (dimensioni konvencional i sferës së mbushur). Megjithatë, nëse gjatësitë njëdimensionale të një fraktali dyfishohen të gjitha, përmbajtja hapësinore e fraktalit shkallëzon me një fuqi që nuk është domosdoshmërisht një numër i plotë dhe në përgjithësi është më i madh se dimensioni i tij konvencional. [1] Kjo fuqi quhet dimensioni fraktal i objektit gjeometrik, për ta dalluar atë nga dimensioni konvencional (i cili zyrtarisht quhet dimension topologjik ). [6]

Analitikisht, shumë fraktale nuk mund të diferencohen askund. [1] [4] Një kurbë fraktale e pafundme mund të konceptohet si dredha-dredha nëpër hapësirë ndryshe nga një vijë e zakonshme - megjithëse është ende topologjikisht 1-dimensionale, dimensioni i saj fraktal tregon se ajo mbush hapësirën në mënyrë më efikase sesa një vijë e zakonshme. [1] [6]

Tapeti i Sierpinskit (deri në nivelin 6), një fraktal me një dimension topologjik 1 dhe një dimension Hausdorff prej 1,893

Duke filluar nga shekulli i 17-të me nocionet e rekursionit, fraktalet kanë kaluar përmes një trajtimi matematikor gjithnjë e më rigoroz në studimin e funksioneve të vazhdueshme por jo të diferencueshme në shekullin e 19-të nga puna kryesore e Bernard Bolzanos, Bernhard Riemannit dhe Karl Vajershtrasit, [7] dhe në krijimin e fjalës fractal në shekullin e 20-të me një rritje të mëvonshme të interesit për fraktale dhe modelimin e bazuar në kompjuter në shekullin e 20-të. [8] [9]

Konsensusi midis matematikanëve është se fraktalet teorike janë konstruksione matematikore të përsëritura dhe të detajuara pafundësisht të ngjashme me vetveten, nga të cilat shumë shembuj janë formuluar dhe studiuar. [1] [2] [3] Fraktalet nuk kufizohen në modele gjeometrike, por gjithashtu mund të përshkruajnë proceset në kohë. [5] [4] [10] [11] [12] [13] Modelet fraktale me shkallë të ndryshme të vetëngjashmërisë janë dhënë ose studiuar në media vizuale, fizike dhe dëgjimore [14] dhe janë gjetur në natyrë, [15] [16] [17] teknologji, [18] [19] [20] art, [21] [22] dhe arkitekturë . [23] Fraktalet janë të një rëndësie të veçantë në fushën e teorisë së kaosit, sepse ato shfaqen në përshkrimet gjeometrike të shumicës së proceseve kaotike (zakonisht ose si tërheqës ose si kufij midis pellgjeve tërheqëse). [24]

  • Kristalet e ngrirjes që krjohen mbi xhamin e ftohtë krijojnë modele fraktale
    Kristalet e ngrirjes që krjohen mbi xhamin e ftohtë krijojnë modele fraktale
  • Kufi i basenit fraktal në një sistem optik gjeometrik
    Kufi i basenit fraktal në një sistem optik gjeometrik
  • Një fraktal formohet kur tërhiqen dy fleta akriliku të mbuluara me ngjitës
    Një fraktal formohet kur tërhiqen dy fleta akriliku të mbuluara me ngjitës
  • High-voltage breakdown within a 4 in (100 mm) block of acrylic glass creates a fractal Lichtenberg figure
    Ndarja e tensionit të lartë brenda një blloku xhami 100 mm akrilik krijon një fraktal Figura e Lihtenbergut
  • Romanesco broccoli, showing self-similar form approximating a natural fractal
    Brokoli romanesko, duke treguari vetëngjashëm formë që përafron një fraktal natyror
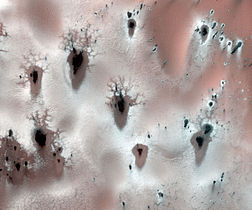
  • Fractal defrosting patterns, polar Mars. The patterns are formed by sublimation of frozen CO2. Width of image is about a kilometer.
    Modelet e shkrirjes fraktale, Marsi polar. Modelet formohen nga sublimimi i CO të ngrirë2. Gjerësia e imazhit është rreth një kilometër.
  • Slime mold Brefeldia maxima growing fractally on wood
    myk zhul Brefeldia maxima duke u rritur në mënyrë fraktale në dru
  • Psilomelane dendrites in the Solnhofen Limestone
    Psilomelani dendritetnëGur gëlqeror Solnhofen
  1. ^ a b c d e Mandelbrot, Benoît B. (1983). The fractal geometry of nature. Macmillan. ISBN 978-0-7167-1186-5. {{cite book}}: Mungon ose është bosh parametri |language= (Ndihmë!) Gabim referencash: Invalid <ref> tag; name "Mandelbrot1983" defined multiple times with different content
  2. ^ a b Falconer, Kenneth (2003). Fractal Geometry: Mathematical Foundations and Applications. John Wiley & Sons. fq. xxv. ISBN 978-0-470-84862-3. {{cite book}}: Mungon ose është bosh parametri |language= (Ndihmë!) Gabim referencash: Invalid <ref> tag; name "Falconer" defined multiple times with different content
  3. ^ a b Briggs, John (1992). Fractals:The Patterns of Chaos. London: Thames and Hudson. fq. 148. ISBN 978-0-500-27693-8. {{cite book}}: Mungon ose është bosh parametri |language= (Ndihmë!) Gabim referencash: Invalid <ref> tag; name "patterns" defined multiple times with different content
  4. ^ a b c Vicsek, Tamás (1992). Fractal growth phenomena. Singapore/New Jersey: World Scientific. fq. 31, 139–146. ISBN 978-981-02-0668-0. {{cite book}}: Mungon ose është bosh parametri |language= (Ndihmë!) Gabim referencash: Invalid <ref> tag; name "vicsek" defined multiple times with different content
  5. ^ a b Gouyet, Jean-François (1996). Physics and fractal structures. Paris/New York: Masson Springer. ISBN 978-0-387-94153-0. {{cite book}}: Mungon ose është bosh parametri |language= (Ndihmë!) Gabim referencash: Invalid <ref> tag; name "Gouyet" defined multiple times with different content
  6. ^ a b Mandelbrot, Benoît B. (2004). Fractals and Chaos. Berlin: Springer. fq. 38. ISBN 978-0-387-20158-0. A fractal set is one for which the fractal (Hausdorff-Besicovitch) dimension strictly exceeds the topological dimension {{cite book}}: Mungon ose është bosh parametri |language= (Ndihmë!) Gabim referencash: Invalid <ref> tag; name "Mandelbrot Chaos" defined multiple times with different content
  7. ^ Segal, S. L. (qershor 1978). "Riemann's example of a continuous 'nondifferentiable' function continued". The Mathematical Intelligencer. 1 (2): 81–82. doi:10.1007/BF03023065. {{cite journal}}: Mungon ose është bosh parametri |language= (Ndihmë!)
  8. ^ Edgar, Gerald (2004). Classics on Fractals. Boulder, CO: Westview Press. ISBN 978-0-8133-4153-8. {{cite book}}: Mungon ose është bosh parametri |language= (Ndihmë!)
  9. ^ Trochet, Holly (2009). "A History of Fractal Geometry". MacTutor History of Mathematics. Arkivuar nga origjinali më 12 mars 2012. {{cite web}}: Mungon ose është bosh parametri |language= (Ndihmë!)
  10. ^ Peters, Edgar (1996). Chaos and order in the capital markets : a new view of cycles, prices, and market volatility. New York: Wiley. ISBN 978-0-471-13938-6. {{cite book}}: Mungon ose është bosh parametri |language= (Ndihmë!)
  11. ^ Krapivsky, P. L.; Ben-Naim, E. (1994). "Multiscaling in Stochastic Fractals". Physics Letters A. 196 (3–4): 168. Bibcode:1994PhLA..196..168K. doi:10.1016/0375-9601(94)91220-3. {{cite journal}}: Mungon ose është bosh parametri |language= (Ndihmë!)
  12. ^ Hassan, M. K.; Rodgers, G. J. (1995). "Models of fragmentation and stochastic fractals". Physics Letters A. 208 (1–2): 95. Bibcode:1995PhLA..208...95H. doi:10.1016/0375-9601(95)00727-k. {{cite journal}}: Mungon ose është bosh parametri |language= (Ndihmë!)
  13. ^ Hassan, M. K.; Pavel, N. I.; Pandit, R. K.; Kurths, J. (2014). "Dyadic Cantor set and its kinetic and stochastic counterpart". Chaos, Solitons & Fractals. 60: 31–39. arXiv:1401.0249. Bibcode:2014CSF....60...31H. doi:10.1016/j.chaos.2013.12.010. {{cite journal}}: Mungon ose është bosh parametri |language= (Ndihmë!)
  14. ^ Brothers, Harlan J. (2007). "Structural Scaling in Bach's Cello Suite No. 3". Fractals. 15 (1): 89–95. doi:10.1142/S0218348X0700337X. {{cite journal}}: Mungon ose është bosh parametri |language= (Ndihmë!)
  15. ^ Liu, Jing Z.; Zhang, Lu D.; Yue, Guang H. (2003). "Fractal Dimension in Human Cerebellum Measured by Magnetic Resonance Imaging". Biophysical Journal. 85 (6): 4041–4046. Bibcode:2003BpJ....85.4041L. doi:10.1016/S0006-3495(03)74817-6. PMC 1303704. PMID 14645092. {{cite journal}}: Mungon ose është bosh parametri |language= (Ndihmë!)
  16. ^ Karperien, Audrey L.; Jelinek, Herbert F.; Buchan, Alastair M. (2008). "Box-Counting Analysis of Microglia Form in Schizophrenia, Alzheimer's Disease and Affective Disorder". Fractals. 16 (2): 103. doi:10.1142/S0218348X08003880. {{cite journal}}: Mungon ose është bosh parametri |language= (Ndihmë!)
  17. ^ Jelinek, Herbert F.; Karperien, Audrey; Cornforth, David; Cesar, Roberto; Leandro, Jorge de Jesus Gomes (2002). "MicroMod-an L-systems approach to neural modelling". përmbledhur nga Sarker, Ruhul (red.). Workshop proceedings: the Sixth Australia-Japan Joint Workshop on Intelligent and Evolutionary Systems, University House, ANU. University of New South Wales. ISBN 978-0-7317-0505-4. OCLC 224846454. Marrë më 3 shkurt 2012. Event location: Canberra, Australia {{cite book}}: Mungon ose është bosh parametri |language= (Ndihmë!)
  18. ^ Hu, Shougeng; Cheng, Qiuming; Wang, Le; Xie, Shuyun (2012). "Multifractal characterization of urban residential land price in space and time". Applied Geography. 34: 161–170. Bibcode:2012AppGe..34..161H. doi:10.1016/j.apgeog.2011.10.016. {{cite journal}}: Mungon ose është bosh parametri |language= (Ndihmë!)
  19. ^ Karperien, Audrey; Jelinek, Herbert F.; Leandro, Jorge de Jesus Gomes; Soares, João V. B.; Cesar Jr, Roberto M.; Luckie, Alan (2008). "Automated detection of proliferative retinopathy in clinical practice". Clinical Ophthalmology. 2 (1): 109–122. doi:10.2147/OPTH.S1579. PMC 2698675. PMID 19668394. {{cite journal}}: Mungon ose është bosh parametri |language= (Ndihmë!)
  20. ^ Losa, Gabriele A.; Nonnenmacher, Theo F. (2005). Fractals in biology and medicine. Springer. ISBN 978-3-7643-7172-2. {{cite book}}: Mungon ose është bosh parametri |language= (Ndihmë!)
  21. ^ Wallace, David Foster (4 gusht 2006). "Bookworm on KCRW". Kcrw.com. Arkivuar nga origjinali më 11 nëntor 2010. Marrë më 17 tetor 2010. {{cite web}}: Mungon ose është bosh parametri |language= (Ndihmë!)
  22. ^ Eglash, Ron (1999). "African Fractals: Modern Computing and Indigenous Design". New Brunswick: Rutgers University Press. Arkivuar nga origjinali më 3 janar 2018. Marrë më 17 tetor 2010. {{cite web}}: Mungon ose është bosh parametri |language= (Ndihmë!)
  23. ^ Ostwald, Michael J., and Vaughan, Josephine (2016) The Fractal Dimension of Architecture Birhauser, Basel. doi:10.1007/978-3-319-32426-5.
  24. ^ Baranger, Michael. "Chaos, Complexity, and Entropy: A physics talk for non-physicists" (PDF). {{cite web}}: Mungon ose është bosh parametri |language= (Ndihmë!)
Marrë nga "https://sq.wikipedia.org/w/index.php?title=Fraktali&oldid=2672737"