Бонавентура Кавалијери

Бонавентура Кавалијери
Кавалијери је увео интегрални рачун
Пуно име	Бонавентура Франческо Кавалијери
Име по рођењу	Бонавентура Францесцо Цавалиери
Друга имена	Бонавентура Цавалиери
Датум рођења	1598
Место рођења	Милано  Миланско војводство
Датум смрти	30. новембар 1647.(1647-11-30) (48/49 год.)
Место смрти	Болоња  Папска држава
Пребивалиште	Италија
Држављанство	италијанско
Универзитет	Универзитет у Пизи
Занимање	математичар
Деловање	Кавалијеријев принцип Кавалијеријева формула квадратуре

Бонавентура Франческо Кавалијери (лат. Cavalerius; 1598 – 30. новембер 1647) био је италихански математичар и јесуат. Он је познат по свом раду на проблема оптике и кретања, раду на недељивости, прекурзорима инфинитезималног рачуна, и увођењу логаритама у италијанску науку. Кавалијеријев принцип у геометрији делимично је предвидео интергрални рачун.

Живот

Рођен у Милану, Кавалијери се придружио јесуатском реду (који не треба мешати са језуитима) у својој петнаестој години, узевши име Бонавентура након што је постао почетник у реду. Он је остао члан тог реда до своје смрти. Завете је положио и постао пуноправни члан реда 1615. године, у узрасту од седамнаест година, и убрзо након тога придружио се јесуатској кући у Пизи. До 1616. био је студент геометрије на Универзитету у Пизи. Тамо је дошао под старатељство Бенедета Кастелија, који га је вероватно упознао са Галилеом Галилејем. Године 1617. на кратко се придружио двору Медичија у Фиренци, под покровитељством кардинала Федерика Боромеа, али се следеће године вратио у Пизу и почео да предаје математику уместо Кастелија. Пријавио се за катедру за математику на Универзитету у Болоњи, али је одбијен.

Године 1620. се вратио у јесуатску кућу у Милану, где је живео као искушеник, и постао је ђакон под кардиналом Боромеом. Студирао је теологију у манастиру Сан Героламо у Милану, а именован је по манастиру Светог Петра у Лодију. Године 1623. постављен је за игумана манастира Светог Бенедикта у Парми, али се још увек пријављивао за математичке позиције. Поново је поднео апликацију за Болоњу, а 1626. године за Универзитет Сапиенца, али је сваки пут одбијен, упркос тога што је узео шест месеци одсуства да подржи своју апликацију на Сапиенци у Риму. Године 1626. почео је да пати од гихта, што ће му ограничити кретање до краја живота. Такође је одбијен за место на Универзитету у Парми, за шта се верује да је било последица његове припадности јесуатском реду, јер је Пармом у то време управљао исусовски ред. Године 1629. постављен је на катедру за математику на Универзитету у Болоњи, што се приписује Галилеовој подршци у Болоњском сенату.

Већи део свог дела објавио је док је био у Болоњи, иако су неки од радова већ били написани. Његов рад Geometria Indivisibilius, где је изнео оно што ће касније постати метод недељивости, написан је 1627. док је био у Парми и представљен као део његове апликације у Болоњи, али није објављен до 1635. Критички пријем његових савременика био је мешовит, а рад Exercitationes geometricae sex (Шест вежби из геометрије) објављено је 1947. године, делом као одговор на критике. Такође у Болоњи објавио је табеле логаритама и информације о њиховој употреби, промовишући њихову употребу у Италији.

Галилео је извршио снажан утицај на Кавалијерија, и Кавалијери је написао Галилеју најмање 112 писама. Галилео је о њему рекао, „неколицина, ако уопште ико, још од Архимеда, продрла је толико далеко и дубоко у науку о геометрији.” Он је одржавао широки кореспонденцију; његови познати дописници су Марина Мерсена, Евангелисту Торичелија и Винченца Вивијанија. Торичели је имао посебно значајну улогу у прочишћавању и промовисању метода недељивости. Такође је имао користи од покровитељства Чезара Марсилија.

Пред крај живота здравље му се знатно погоршало. Артритис га је спречавао да пише, и велики део своје преписке диктирао је Стефану дегли Анђелију, колеги јесуату и Кавалијеривом студенту. Анђели је касније наставио да развија Кавалијеријеву методу.

Године 1647. је умро, вероватно од гихта.

Рад

Од 1632. до 1646. Кавалијери је објавио једанаест књига које су се бавиле проблемима у астрономији, оптици, кретању и геометрији.

Рад у оптици

Кавалиријева прва књига, први пут објављена 1632. и поново штампана 1650. године, била је Ло Спеццхио Усторио, оверо, Траттато делле сеттиони цоницхе, или Горуће огледало, или Трактат о конусним пресецима. Циљ дела Ло Спеццхио Усторио је био да се позабави питањем како је Архимед могао да користи огледала да спали римску флоту док су се приближавале Сиракузи, питање које се још увек дебатује Књига је превазишла ову сврху, те је такође истраживала коничне пресеке, рефлексије светлости и својства парабола. У овој књизи је развио теорију огледала уобличених у параболе, хиперболе и елипсе и разне комбинације ових огледала. Он је показао да ако, као што је касније показано, светлост има коначну и одређену брзину, постоји минимална интерференција у слици у фокусу параболичног, хиперболичног или елиптичног огледала, иако је то била теоретска поставка, пошто се потребна огледала нису могла конструисати користећи тадашњу технологију. Ово би произвело боље слике у телескопима који су постојали у то време.

Геометријске фигуре из Ло Спеццио Усторио, коришћене у доказима својстава параболичких рефлектујућих површина.

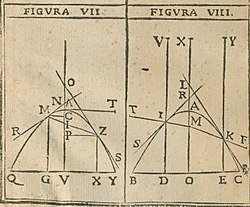
Он је такође показао нека својства кривих. Прво је да је за светлосни зрак паралелан са осом параболе и рефлектован тако да прође кроз фокус, збир упадног угла и његовог одраза једнак оном било ког другог сличног зрака. Затим је показао сличне резултате за хиперболе и елипсе. Други резултат, користан у дизајну рефлектујућих телескопа, је да ако се линија продужи од тачке изван параболе до фокуса, онда је одраз ове линије на спољној површини параболе паралелан са осом. Други резултати укључују особину да ако линија пролази кроз хиперболу и њен спољашњи фокус, онда ће њен одраз на унутрашњост хиперболе проћи кроз унутрашњи фокус; обрнуто од претходног је да се зрак усмерен кроз параболу ка унутрашњем фокусу рефлектује од спољашње површине ка спољашњем фокусу; и својство да ако линија пролази кроз један унутрашњи фокус елипсе, њен одраз на унутрашњој површини елипсе пролази кроз други унутрашњи фокус. Док су нека од ових својстава била раније забележена, Кавалиери је дао први доказ многих.

Дело Ло Спеццхио Усторио је такође садржало табелу рефлектујућих површина и начина рефлексије за практичну употребу.

Кавалијеров рад је такође садржао теоријске дизајне за нови тип телескопа који користи огледала, рефлектујући телескоп, који је првобитно развијен да одговори на питање Архимедовог огледала, а затим примењен у много мањој скали као телескопи. Он је илустровао три различита концепта за уградњу рефлектујућих огледала у свој модел телескопа. Први план се састојао од великог, конкавног огледала усмереног ка сунцу да рефлектује светлост у друго, мање, конвексно огледало. Кавалијеров други концепт се састојао од главног, скраћеног, параболоидног огледала и другог, конвексног огледала. Његова трећа опција је илустровала снажну сличност са његовим претходним концептом, заменивши конвексно секундарно сочиво конкавним сочивом.

Рад у геометрији и на методу недељивости

Насловна страна дела Геометриа индивисибилибус.

Инспирисан ранијим Галилејевим радом, Кавалијери је развио нови геометријски приступ назван методом недељивих рачунању и објавио расправу на ту тему,Геометриа индивисибилибус цонтинуорум нова qуадам ратионе промота, или Геометрија, развијена новом методом кроз недељиве континуума. Ово је написано 1627. године, али је објављено тек 1635. У овом раду, Кавалијери разматра ентитет који се у тексту помиње као 'све линије' или 'све равни' фигуре, неодређени број паралелних правих или равни унутар граница фигуре које су упоредиве са површином и запремином фигуре. Каснији математичари, побољшавајући његову методу, третирали би 'све праве' и 'све равни' као еквивалентне или једнаке површини и запремини, али је Кавалијери, у покушају да избегне питање састава континуума, инсистирао да су ова два појма била упоредива, али не и једнака.

Ови паралелни елементи се називају недељивим по површини и запремини и представљају градивне блокове Кавалијеријеве методе, а такође су и фундаменталне карактеристике интегралног рачуна. Такође је користио метод недељивих да израчуна резултат који је сада записује као $\int _{0}^{1}x^{2}dx=1/3$, у процесу израчунавања површине затворене у Архимедову спиралу, коју је касније генерализовао на друге фигуре, показујући, на пример, да је запремина конуса једна трећина запремине.

Литература

• Елогј ди Галилео Галилеи е ди Бонавентура Цавалиери бy Гиусеппе Галеаззи, Милан, 1778
• Бонавентура Цавалиери бy Антонио Фаваро, вол. 31 оф Амици е цорриспонденти ди Галилео Галилеи, C. Феррари, 1915.
• Фаброни, Ангело (1778). „Бонавентура Цавалериус”. Витае Италорум доцтрина еxцеллентиум qуи саецулис XVII. ет XVIII. флоруерунт (на језику: латински). Писа. I: 262—301. 

Спољашње везе

• The Galileo Project: Cavalieri
• Онлајн текстови Кавалијерија:
  • Ло спеццхио усторио: оверо, Траттато делле сеттиони цоницхе... (1632)
  • Дирецториум генерале уранометрицум (1632)
  • Геометриа Индивисибилибус (1653)
  • Сфера астрономица (1690)
• Биограпхиес:
  • О'Цоннор, Јохн Ј.; Робертсон, Едмунд Ф. „Бонавентура Кавалијери”. МацТутор Хисторy оф Матхематицс арцхиве. Университy оф Ст Андреwс. 
  • Схорт биограпхy он боокрагс.цом
• Модерн матхематицал ор хисторицал ресеарцх:
  • Инфинитесимал Цалцулус Он итс хисторицал девелопмент, ин Енцyцлопаедиа оф Матхематицс, Мицхиел Хазеwинкел ед.
  • Море информатион абоут тхе метход оф Цавалиери
  • Цавалиери Интегратион