Quantifying Phase-Amplitude Modulation in Neural Data

Victoria Subritzky-Katz; Aaron L Sampson; Erik Emeric; Witold Lipski; Sophia Moreira-González; Jorge González-Martínez; Sridevi Sarma; Veit Stuphorn; Ernst Niebur

doi:10.1109/CISS56502.2023.10089691

. Author manuscript; available in PMC: 2024 Jan 20.

Published in final edited form as: Annu Conf Inf Sci Syst. 2023 Apr 10;2023:10.1109/CISS56502.2023.10089691. doi: 10.1109/CISS56502.2023.10089691

Quantifying Phase-Amplitude Modulation in Neural Data

Victoria Subritzky-Katz ^1,^*,^†, Aaron L Sampson ^2,^*, Erik Emeric ³, Witold Lipski ⁴, Sophia Moreira-González ⁵, Jorge González-Martínez ⁶, Sridevi Sarma ⁷, Veit Stuphorn ⁸, Ernst Niebur ⁹

PMCID: PMC10799684 NIHMSID: NIHMS1955013 PMID: 38250522

Abstract

Phase-amplitude modulation (the modulation of the amplitude of higher frequency oscillations by the phase of lower frequency oscillations) is a specific type of cross-frequency coupling that has been observed in neural recordings from multiple species in a range of behavioral contexts. Given its potential importance, care must be taken with how it is measured and quantified. Previous studies have quantified phase-amplitude modulation by measuring the distance of the amplitude distribution from a uniform distribution. While this method is of general applicability, it is not targeted to the specific modulation pattern frequently observed with low-frequency oscillations. Here we develop a new method that has increased specificity to detect modulation in the sinusoidal shape commonly observed in neural data.

Keywords: phase-amplitude modulation, cross-frequency coupling, sEEG, EEG, ECoG

I. Introduction

Modulation of high-frequency amplitude by low-frequency phase is a widely studied measure of EEG and intracranial activity [1]. In particular, gamma (40-70 Hz) amplitude modulation by theta (4-8 Hz) phase has been previously reported in electrocorticogram (ECoG) recordings from patients performing a variety of language and motor tasks (passive listening, linguistic target detection, verb generation, hand and mouth motor activation, auditory working memory, auditory-vibrotactile target detection) [2]. Theta-gamma phase-amplitude modulation in the hippocampus has been linked to short-term [3] and working memory [4]. In the domain of decision making, theta-gamma phase-amplitude modulation has previously been reported in the orbitofrontal cortex of rodents in an olfactory discrimination go/nogo task [5]. Phase-amplitude coupling has also been observed in humans performing decision-making tasks, specifically, theta-gamma and theta-delta coupling in the medial frontal cortex has been shown to be related to feedback valence [6].

In this contribution, we report significant theta-gamma phase-amplitude modulation in human patients instrumented with stereotactic electroencephalogram (sEEG) electrodes during option selection, outcome anticipation, and feedback stages of a multi-attribute decision task. We start by developing a novel method to characterize phase-amplitude correlations based on the specific (approximately sinusoidal) shape of the observed modulation of gamma band amplitude by theta band phase, and then apply it to neural data recorded intracranially in human patients.

II. Methods

A. Curve Fitting

A commonly used method to quantify phase-amplitude modulation computes a Modulation Index from the Kullback-Leibler distance from a uniform amplitude distribution across phase [7]. This approach is equally sensitive to any deviation from uniform amplitude across phase and therefore makes no particular assumptions about any specific structure in the modulation, i.e. a particular functional relationship between phase and amplitude. While this may be a desirable feature of the method in many cases, it is often the case that phase-amplitude modulation in neural signals does show a more consistent structure. With our novel method, we seek to capture this structure. Rather than measuring the deviation of amplitude as a function of phase from uniformity in any way, we will selectively target a presumed functional form. Here, we use a first-order sinusoid, as this seems to be generally reflective of the pattern of modulation we observe in neural data (see Section IV for a discussion of this choice). Fig. 1 shows examples of synthetic data with strong modulation that do (panels A,B) or do not (C,D) follow a clear sinusoidal form, resulting in very similar Modulation Indices (MI), but markedly different fitting errors from a sinuoid ( $ρ_{s i n}$ , defined below).

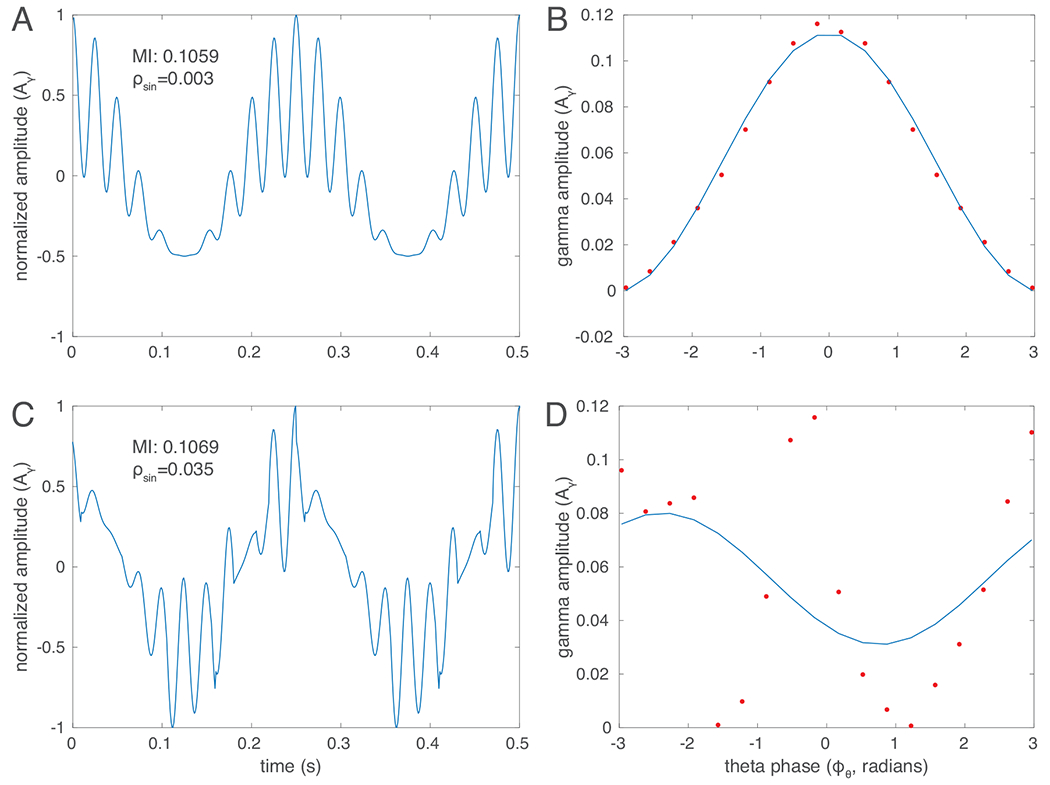
Fig. 1. — Different types of phase-amplitude modulation illustrated with synthetic data. A and C show a 40 Hz (gamma) oscillation modulated in amplitude by the phase of a 4 Hz (theta) oscillation. In A, amplitude is high around the peak of the theta waves and low around the trough of the theta waves. This pattern is well-fit a by a first order sinusoid (shown in B). In C, gamma amplitude is strongly modulated by the phase of the theta oscillation, but this modulation does not follow a pattern that would be well fit by a simple functional form. Both types of modulation result in a similar value of the Modulation Index based on a KL divergence from the uniform distribution (MI), but result in very different errors in the fit to the sinusoid ( $ρ_{\sin})$ , see eq. 2).

Intracranial stereo EEG recordings (sEEG) were performed in human patients (see Section II-C) while they performed a multi-attribute decision task (Section II-D). To characterize phase-amplitude modulation, sEEG time series data are first aligned to some time point of interest, e.g. the time at which feedback (on gain or loss of reward) is delivered. Data are then subjected to bandpass filtering to select the two frequency bands of interest, e.g. theta (4–8 Hz) and gamma/high gamma (40–200 Hz; for simplicity we will refer to this whole range as gamma). Here, we denote these bandpass-filtered signals $θ (t)$ and $γ (t)$ , although any frequency bands of interest could be substituted. Phase information is extracted from the lower-frequency $(θ)$ filtered data via Hilbert transform, i.e. the phase $ϕ_{θ} (t) = \arg [ℋ (θ (t))]$ ; we used the $angle (hilbert (x))$ function from Matlab (Mathworks Inc., Natick MA). This low-frequency phase information is then sorted into 18 equal-width bins, each corresponding to $π / 9$ radians. The amplitude of the normalized high-frequency-filtered $(γ)$ data across all event-aligned time periods of interest is then computed and averaged across all epochs when the phase of the theta oscillation falls into a given bin. Figs. 2 and 3 show examples of these epochaveraged gamma amplitudes across phase bins of theta for two recording contacts. The gamma amplitude is well-correlated with theta phase in the latter but not in the former contact.

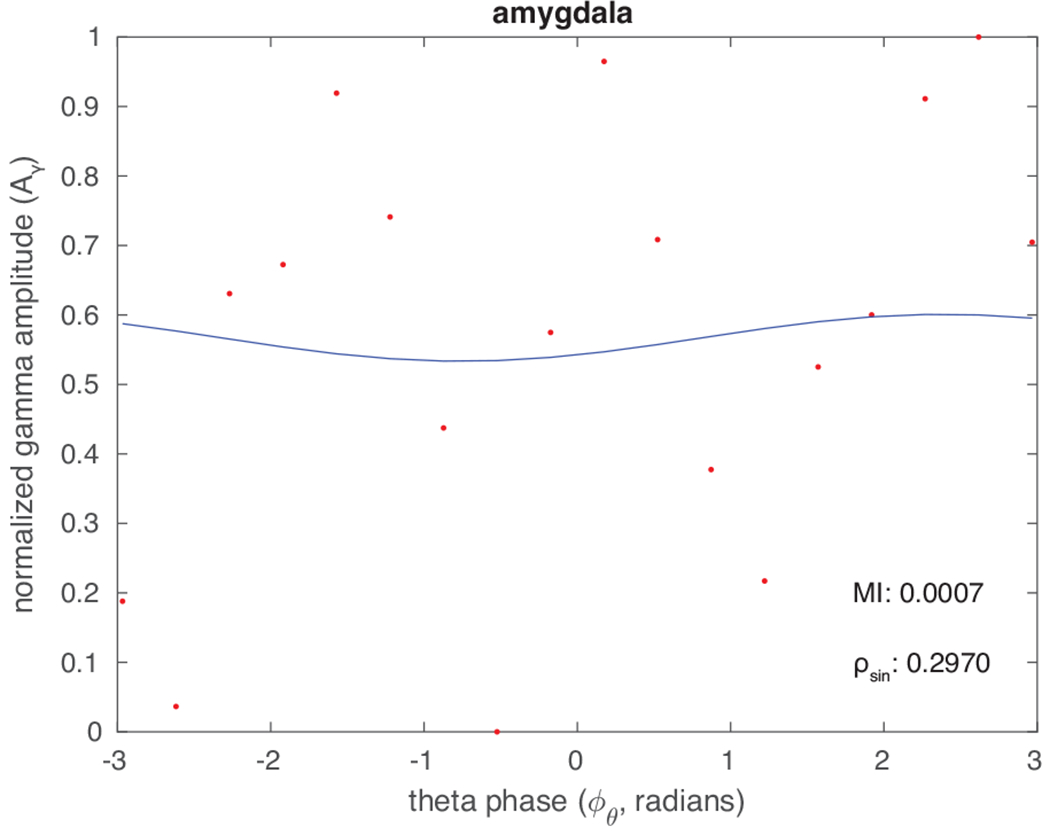
Fig. 2. — Theta-phase gamma-amplitude relation from one sEEG electrode located in the amygdala. The panel shows an example of gamma amplitude (red circles) with no clear structure in its relation to theta phase. The blue line is the best sinusoidal fit for the gamma amplitude data.

Fig. 3. — Theta-phase gamma-amplitude relation in the hippocampus, from a different sEEG electrode than in Fig 2. Here, the gamma amplitude closely follows a sinusoidal function of theta phase. Symbols as in Fig 2.

Let us denote these epoch-averaged amplitudes as $A_{γ} (ϕ_{θ})$ . In order to quantify the phase-amplitude modulation that follows an assumed functional form, we can fit these amplitudes to that function. While any periodic function (with its attendant assumptions) could be employed in this step, one simple functional form that is essentially consistent with the typically observed features of phase-amplitude modulation in neural data is a sinusoid. Therefore, we fit $A_{γ} (ϕ_{θ})$ to a curve defined by:

f (ϕ_{θ}) = a_{0} + a_{1} cos ϕ_{θ} + b_{1} sin ϕ_{θ} .

(1)

We determine the values of the parameters $a_{0}, a_{1}$ , and $b_{1}$ by minimizing the least-squares error:

ρ_{s i n} = \sqrt{\frac{\sum A_{γ} (ϕ_{θ}) - {(a_{0} + a_{1} cos ϕ_{θ} + b_{1} sin ϕ_{θ})}^{2}}{n_{b i n s}}}

(2)

Based on the fit curve, we can quantify the modulation present in several ways. First, the value of the least-squares error $ρ_{\sin}$ itself indicates where there exists a clear structure of $A_{γ} (ϕ_{θ})$ in the form of a sinuoid. Also of interest is the depth of the modulation, i.e. the difference between maximum and minimum of $A_{γ}$ as predicted by the best-fit sinusoid. Finally, of particular interest are the phase bins at which the minimum and maximum of this function occur, $ϕ_{\max}$ and $ϕ_{\min}$ .

B. Permutation Testing

To test significance of our results, for a given electrode and time period, the gamma amplitudes across theta phase bins, $A_{γ} (ϕ_{θ})$ , are calculated and then the amplitudes are shuffled across the phase bins 10,000 times. Each iteration within this shuffled distribution is fit to a sinusoid and the least-squares error for each is calculated. An electrode is considered to show significant modulation if the error of fit of a sinusoid to the real data is lower than 99% of the shuffled data (p < 0.01).

C. Neural Recordings

Simultaneous behavioral and neural data were recorded from four patients with implanted stereotactic electroencephalogram electrodes using a tablet-based multi-attribute decision making task. Data were collected at the University of Pittsburgh Medical Center. All sEEG recordings come from patients who are undergoing treatment for medically intractable focal epilepsy. Patients are implanted with electrodes according to their clinical care plan and then placed under observation until sufficient seizure data are collected to develop a plan for surgical intervention. Neither this nor any other research study has any influence on the location of the implanted electrodes and accordingly, different patients have data from different brain regions. Fig. 4A shows an example of the placement of sEEG electrodes in one patient.

Fig. 4. — Tablet-based multi-attribute decision making task and intracranial recordings. A. Example of sEEG electrode placement in one patient. B. Screenshot of the tablet-based multi-attribute decision task. Here, two options are presented, each of which has two attributes: a probability of winning and amount to win. When an attribute is tapped, the underlying value is unmasked for 1s, here the probability of winning of the upper option

D. Multi-Attribute Decision Task

Patients are presented with two options (gambles) on an electronic tablet screen. Each option corresponds to the possibility of winning or losing virtual money (neutral outcomes are also possible). On a given trial, either two winning or two losing options are presented. Each option is defined by two attributes, the amount they can win or lose, and the probability that this will happen. Importantly, the values of these attributes are “hidden” originally. Instead of each value, a colored symbol is shown that indicates what value is “hidden” beneath it, as follows: winning amount: green dollar sign; winning probability: green dice symbol; losing amount: red dollar sign; losing probability: red dice symbol. Only when a patient taps on the disk the value is revealed for 1s (or until the patient taps another symbol). They can look back at each option as many times as they want, by tapping on its red or green symbols. Once they have decided which of the gambles they want to bet on, they tap its “select” button. The properties of their chosen gamble (amounts and probabilities) will be briefly displayed, and after that, the screen will show the outcome, i.e. how much virtual money they have won or lost in this round. Fig. 4B shows a screenshot of the multiattribute decision making task in use with one attribute (win probability for option 1) unmasked.

III. Results

We apply our new approach to quantifying phase-amplitude modulation to sEEG recordings from four patients. Figure 5 summarizes the phase-amplitude modulation results for a set of recording locations from one patient that showed significant theta-gamma phase-amplitude modulation in the time period aligned to feedback, separated by whether the outcome of the trial was positive (win or avoided loss) or negative (loss or failure to win). Of note, several recordings from the orbitofrontal cortex show signficant phase-amplitude modulation only following positive outcomes (left panel, colored rows), but not following negative outcomes (right panel, white rows).

Fig. 5. — Recording contacts with significant phase-amplitude modulation in one patient. Each row corresponds to a single recording location for the one-second time period immediately following feedback presentation for positive (left) and negative (right) outcomes. Red shades correspond to relatively higher gamma amplitude and blue shades correspond to relatively lower gamma amplitude. Gamma amplitude is normalized relative to the mean gamma amplitude for each recording contact. For electrodes in which only one of the conditions showed significant phase-amplitude modulation, the corresponding row for the other condition is shown in white.

Another noteworthy feature of the observed modulation patterns is that the highest gamma-band amplitude tends to fall either close to the peak $(ϕ_{θ} = 0)$ or the trough $(ϕ_{θ} = \pm π)$ of the theta oscillation. We call the former situation “peak-max” and the latter “trough-max”, see below for a formal definition (note that no particular phase of the fit sinusoid is assumed in the curve-fitting procedure). This feature of the modulation is consistent with previous reports [8], [9] and underscores the rationale for defining a measure of phase-amplitude modulation that is based on a functional form with only one local maximum and one local minimum per cycle.

Table I summarizes the prevalence of significant phase-amplitude modulation in sEEG recordings from four patients. Part A lists the total number of recording contacts that show significant modulation for each patient and alignment point relative to the total number of contacts during the anticipation and feedback time periods (columns 2, 3). Also shown are the numbers of contacts in which significant phase-amplitude modulation was found when the outcome was positive (column 4) or negative (column 5). For all four patients, the number of contacts with significantly higher phase-amplitude modulation for positive outcomes exceeded that in which the modulation was higher for negative outcomes. These differences were significant for patients 1 and 4 (p < 0.05, Fisher’s Exact Test).

TABLE I.

Prevalence of phase-amplitude modulation in sEEG recordings from four patients.

A	total number of contacts with significant modulation
patient	anticipation	feedback	positive outcome	negative outcome
1	67/138	70/138	58/138	34/138
2	46/189	40/189	42/189	35/189
3	15/225	13/225	13/225	11/225
4	150/254	143/254	118/254	90/254
B	peak-max: $- π / 2 < arg max (A_{γ} (ϕ_{θ})) < π / 2$
patient	anticipation	feedback	positive outcome	negative outcome
1	42/67	43/70	32/58	17/34
2	21/46	4/40	11/42	4/35
3	7/15	8/13	5/13	8/11
4	72/150	86/143	62/118	60/90
C	trough-max: $arg max (A_{γ} (ϕ_{θ})) < - π / 2$ or $arg max (A_{γ} (ϕ_{θ})) > π / 2$
patient	anticipation	feedback	positive outcome	negative outcome
1	25/67	27/70	24/58	16/34
2	18/46	35/40	25/42	30/35
3	7/15	5/13	8/13	2/11
4	65/150	49/143	48/118	24/90

Open in a new tab

In Parts B and C, the number of contacts with two specific types of modulation are shown relative to the total number of contacts with significant modulation. The two modulation patterns are defined by the values of $ϕ_{θ}$ at which $A_{γ} (ϕ_{θ})$ is at its maximum. Recall that the peak of the theta wave is at phase $ϕ_{θ} = 0$ . If the maximum of gamma amplitude, i.e the maximum of $A_{γ} (ϕ_{θ})$ , is within the interval $ϕ_{θ} \in [- π / 2, π / 2]$ , it is labeled peak-max modulation and included in Part B of the Table. If the maximum of $A_{γ} (ϕ_{θ})$ is in the union of the intervals $[- π, - π / 2]$ and $[π / 2, π]$ , it is labeled trough-max modulation and listed in Part C. Across all patients, subsets of channels show peak-max and trough-max modulation of gamma amplitude. The prevalence of significant phase-amplitude modulation at the analyzed time points varies considerably between patients, each with different electrode placement. But broadly, numerous recordings do show significant modulation.

IV. Limitations

A limitation of our method is that we assume a sinusoidal wave form for the low-frequency (theta) wave while brain oscillations can deviate from sinusoidal shapes (review: ref [10]). This is of relevance for our approach since non-sinusoidal waveforms can result in the “detection” of artifactual phase-amplitude coupling [11]. Another issue is that oscillations may not always be present, a situation not covered in the standard spectral (Fourier) framework. New methods have been developed to identify periods when oscillations are present vs. when they are not, such as delay differential analysis [12].

As a practical matter, inspection of the relationship between gamma amplitude and theta phase should reveal any drastic deviations from sinusoidal theta behavior and result in a poor fit, i.e. a large value of $ρ_{\sin}$ in eq 2. An example of a poor fit is shown in Fig 2; this may be due to excessive noise, absence of phase-amplitude coupling, or a theta waveform that is dramatically different from a sinusoid. In contrast, the good fit shown in Fig 3 inspires confidence that the assumption of sinusoidal theta is justified.

In any case, if it is suspected either by a poor fit or by other considerations that the theta wave is not sinusoidal, it is easy to generalize our method to other wave shapes by changing eq. 1 to other functional dependencies and then fit the physiological data to this function. However, given the widespread use of spectral (Fourier) methods in the field, we expect that in many cases eq. 1 will be applicable without any change being needed.

V. Discussion and Conclusions

Given the potential importance of phase-amplitude modulation to the neural mechanisms of diverse cognitive processes, it is of critical importance to clarify the assumptions inherent in how the phenomenon is quantified. Often, a strict definition that includes a presumed functional form is desirable. Here, we propose a measurement of phase-amplitude modulation based on the least-squares error in a fit to a first-order sinusoid. This measure is conceptually simple and well-suited to a particular type of phase-amplitude modulation that we observe in a number of locations in sEEG recordings from patients engaging in a multi-attribute decision task. The general framework of this method could be readily applied to quantify other types of modulation by fitting the observed $A (ϕ)$ to other functions such as higher-order sinusoids, sawtooths, or square waves. Further, this method is complementary to the Modulation Index based on a divergence-from-the uniform distribution, as it is selective for a specific type of modulation that would also be captured in by that index.

Acknowledgments

This work was supported by NSF grant 1835202, NIH/NIDA grant R01DA040990, ONR grant N00014-22-1-2699, and a NIH D-SPAN K00 Fellowship.

Contributor Information

Victoria Subritzky-Katz, Zanvyl Krieger Mind/Brain Institute, Johns Hopkins University, Baltimore, MD, USA.

Aaron L. Sampson, Zanvyl Krieger Mind/Brain Institute, Johns Hopkins University, Baltimore, MD, USA.

Erik Emeric, Zanvyl Krieger Mind/Brain Institute, Johns Hopkins University, Baltimore, MD, USA.

Witold Lipski, Cortical Systems Lab, University of Pittsburgh Medical School, Pittsburgh, PA, USA.

Sophia Moreira-González, Cortical Systems Lab, University of Pittsburgh Medical School, Pittsburgh, PA, USA.

Jorge González-Martínez, Department of Neurosurgery, University of Pittsburgh Medical School, Pittsburgh, PA, USA.

Sridevi Sarma, Department of Biomedical Engineering, Johns Hopkins University, Baltimore, MD, USA.

Veit Stuphorn, Zanvyl Krieger Mind/Brain Institute, Johns Hopkins University, Baltimore, MD, USA.

Ernst Niebur, Zanvyl Krieger Mind/Brain Institute, Johns Hopkins University, Baltimore, MD, USA.

References

[1].Canolty RT and Knight RT, “The functional role of cross-frequency coupling”, Trends in Cognitive Sciences, vol. 14(11), pp. 506–515, November 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
[2].Canolty RT, Edwards E, Dalal SS, Soltani M, Nagarajan SS, Kirsch HE, Berger MS, Barbaro NM, and Knight RT, “High gamma power is phase-locked to theta oscillations in human neocortex”, Science, vol. 313(5793), pp. 1626–1628, September 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
[3].Lisman JE and Idiart MAP, “Storage of 7 plus minus 2 short term memories in oscillatory subcycles”, Science, vol. 267, pp. 1512–1515, 1995. [DOI] [PubMed] [Google Scholar]
[4].Axmacher N, Henseler MM, Jensen O, Weinreich I, Elger CE, and Fell J, “Hippocampal theta-gamma coupling reflects state-dependent information processing in decision making”, Proceedings of the National Academy of Sciences, vol. 107(7), pp. 3228–3233, February 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
[5].van Wingerden M, van der Meij R, Kalenscher T, Maris E, Pennartz CMA, “Phase-amplitude coupling in rat orbitofrontal cortex discriminates between correct and incorrect decisions during associative learning”, Journal of Neuroscience, vol. 34(2), pp. 493–505, January 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
[6].Cohen MX, Elger CE, and Fell J, “Oscillatory activity and phase–amplitude coupling in the human medial frontal cortex during decision making”, Journal of Cognitive Neuroscience, vol. 21(2), pp. 390–402, February 2008. [DOI] [PubMed] [Google Scholar]
[7].Tort ABL, Komorowski R, Eichenbaum H, and Kopell N, “Measuring phase-amplitude coupling between neuronal oscillations of different frequencies”, Journal of Neurophysiology, vol. 104(2), pp.1195–1210, August 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
[8].Mukamel EA, Wong KF, Prerau MJ, Brown EN, and Purdon PL, “Phase-based Measures of Cross-Frequency Coupling in Brain Electrical Dynamics under General Anesthesia”, IEEE EMBS 2011, pp. 1981–1984, Aug. 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
[9].Sampson AL, Babadi B, Prerau MJ, Mukamel EA, Brown EN, and Purdon PL, “A Beamforming Approach to Phase-Amplitude Modulation Analysis of Multi-Channel EEG”, IEEE EMBS 2012, pp. 6731–6734, Sep. 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
[10].Cole SR and Voytek B, “Brain oscillations and the importance of waveform shape”, Trends in Cognitive Neuroscience, vol. 21(2), pp. 137–149, 2017. [DOI] [PubMed] [Google Scholar]
[11].Gerber EM, Sadeh B, Ward A, Knight RT, and Deouell LY, “Non-sinusoidal activity can produce cross-frequency coupling in cortical signals in the absence of functional interaction between neural sources”, PloS One, vol. 11(12), pp. e0167351, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
[12].Sampson AL, Lainscsek C, Gonzalez CE, Ulbert I, Devinsky O, Fabó D, Madsen JR, Halgren E, Cash SS, and Sejnowski TJ, “Delay differential analysis for dynamical sleep spindle detection”, Journal of Neuroscience Methods, vol. 316, pp. 12–21, January 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R1] [1].Canolty RT and Knight RT, “The functional role of cross-frequency coupling”, Trends in Cognitive Sciences, vol. 14(11), pp. 506–515, November 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R2] [2].Canolty RT, Edwards E, Dalal SS, Soltani M, Nagarajan SS, Kirsch HE, Berger MS, Barbaro NM, and Knight RT, “High gamma power is phase-locked to theta oscillations in human neocortex”, Science, vol. 313(5793), pp. 1626–1628, September 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R3] [3].Lisman JE and Idiart MAP, “Storage of 7 plus minus 2 short term memories in oscillatory subcycles”, Science, vol. 267, pp. 1512–1515, 1995. [DOI] [PubMed] [Google Scholar]

[R4] [4].Axmacher N, Henseler MM, Jensen O, Weinreich I, Elger CE, and Fell J, “Hippocampal theta-gamma coupling reflects state-dependent information processing in decision making”, Proceedings of the National Academy of Sciences, vol. 107(7), pp. 3228–3233, February 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R5] [5].van Wingerden M, van der Meij R, Kalenscher T, Maris E, Pennartz CMA, “Phase-amplitude coupling in rat orbitofrontal cortex discriminates between correct and incorrect decisions during associative learning”, Journal of Neuroscience, vol. 34(2), pp. 493–505, January 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R6] [6].Cohen MX, Elger CE, and Fell J, “Oscillatory activity and phase–amplitude coupling in the human medial frontal cortex during decision making”, Journal of Cognitive Neuroscience, vol. 21(2), pp. 390–402, February 2008. [DOI] [PubMed] [Google Scholar]

[R7] [7].Tort ABL, Komorowski R, Eichenbaum H, and Kopell N, “Measuring phase-amplitude coupling between neuronal oscillations of different frequencies”, Journal of Neurophysiology, vol. 104(2), pp.1195–1210, August 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R8] [8].Mukamel EA, Wong KF, Prerau MJ, Brown EN, and Purdon PL, “Phase-based Measures of Cross-Frequency Coupling in Brain Electrical Dynamics under General Anesthesia”, IEEE EMBS 2011, pp. 1981–1984, Aug. 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R9] [9].Sampson AL, Babadi B, Prerau MJ, Mukamel EA, Brown EN, and Purdon PL, “A Beamforming Approach to Phase-Amplitude Modulation Analysis of Multi-Channel EEG”, IEEE EMBS 2012, pp. 6731–6734, Sep. 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R10] [10].Cole SR and Voytek B, “Brain oscillations and the importance of waveform shape”, Trends in Cognitive Neuroscience, vol. 21(2), pp. 137–149, 2017. [DOI] [PubMed] [Google Scholar]

[R11] [11].Gerber EM, Sadeh B, Ward A, Knight RT, and Deouell LY, “Non-sinusoidal activity can produce cross-frequency coupling in cortical signals in the absence of functional interaction between neural sources”, PloS One, vol. 11(12), pp. e0167351, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R12] [12].Sampson AL, Lainscsek C, Gonzalez CE, Ulbert I, Devinsky O, Fabó D, Madsen JR, Halgren E, Cash SS, and Sejnowski TJ, “Delay differential analysis for dynamical sleep spindle detection”, Journal of Neuroscience Methods, vol. 316, pp. 12–21, January 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

Quantifying Phase-Amplitude Modulation in Neural Data

Victoria Subritzky-Katz

Aaron L Sampson

Erik Emeric

Witold Lipski

Sophia Moreira-González

Jorge González-Martínez

Sridevi Sarma

Veit Stuphorn

Ernst Niebur

Abstract

I. Introduction