Abstract
Effective fusion of structural magnetic resonance imaging (sMRI) and functional magnetic resonance imaging (fMRI) data has the potential to boost the accuracy of infant age prediction thanks to the complementary information provided by different imaging modalities. However, functional connectivity measured by fMRI during infancy is largely immature and noisy compared to the morphological features from sMRI, thus making the sMRI and fMRI fusion for infant brain analysis extremely challenging. With the conventional multimodal fusion strategies, adding fMRI data for age prediction has a high risk of introducing more noises than useful features, which would lead to reduced accuracy than that merely using sMRI data. To address this issue, we develop a novel model termed as disentangled-multimodal adversarial autoencoder (DMM-AAE) for infant age prediction based on multimodal brain MRI. Specifically, we disentangle the latent variables of autoencoder into common and specific codes to represent the shared and complementary information among modalities, respectively. Then, cross-reconstruction requirement and common-specific distance ratio loss are designed as regularizations to ensure the effectiveness and thoroughness of the disentanglement. By arranging relatively independent autoencoders to separate the modalities and employing disentanglement under cross-reconstruction requirement to integrate them, our DMM-AAE method effectively restrains the possible interference cross modalities, while realizing effective information fusion. Taking advantage of the latent variable disentanglement, a new strategy is further proposed and embedded into DMM-AAE to address the issue of incompleteness of the multimodal neuroimages, which can also be used as an independent algorithm for missing modality imputation. By taking six types of cortical morphometric features from sMRI and brain functional connectivity from fMRI as predictors, the superiority of the proposed DMM-AAE is validated on infant age (35 to 848 days after birth) prediction using incomplete multimodal neuroimages. The mean absolute error of the prediction based on DMM-AAE reaches 37.6 days, outperforming state-of-the-art methods. Generally, our proposed DMM-AAE can serve as a promising model for prediction with multimodal data.
Index Terms—: Infant age prediction, autoencoder, multimodal machine learning, magnetic resonance imaging
I. Introduction
Neuroimaging-based age prediction is important for brain development analysis and early detection of neurodevelopmental disorders [1]. The discrepancy between the “chronological age” and the predicted “brain age” can be considered as an index of deviation from the normative developmental or aging trajectory. For example, the predicted age with neuroimaging data can be used to detect accelerated atrophy after traumatic brain injury [2] and accelerated brain aging due to schizophrenia [3], type-2 diabetes mellitus [4], and HIV disease [5]. Furthermore, prediction of brain age is also used to help discern possible environmental and lifestyle related influences on the human brain, e.g., younger brain age due to higher education, more self-reported physical activity [6], and long-term meditation practice [7], as well as increased brain age associated with midlife [8].
Since different modalities of neuroimages can provide complementary information to each other, researchers started to combine multimodal imaging to predict brain age. For example, to capture cognitive impairment, functional connectivity derived from rs-fMRI and cortical morphological features from sMRI were combined for brain age prediction [9]. In [10], T2-weighted, T1-weighted, diffusion-weighted, and fluid-attenuate diversion recovery (FLAIR) scans were combined for age prediction, which highlighted the importance of using multimodal biomarkers to study normal aging.
Although many studies on age prediction based on unimodal or multimodal neuroimages have been carried out, little has been dedicated on predicting infant age due to the difficulties in image acquisition and processing. On the other hand, the first two years after birth witness the most critical and dynamic postnatal development in brain structure [11], [12] and function [13], which could largely shape later cognitive and behavioral development. Thus, understanding the underlying patterns and identification of essential biomarkers of brain development during the first two postnatal years are pivotal. Although some quantitative analyses of the development of the infant brain measures [11], [12], [14] have been conducted and many insightful results have been discovered, the traditional group-level comparisons they used are not adequate to precisely identify abnormal brain development at individual level [15]. Comparing to the group-level study, individualized age prediction is a better way to understand and model the subject-specific brain development. Although it has been found in older populations multimodal MRI data can boost age prediction accuracy [9], [10], it remains unclear whether it still holds in infants.
To the best of our knowledge, there is no study on multi-modal neuroimaging-based infant age prediction. To fill this critical gap and identify potential biomarkers of infant brain development with multiple imaging modalities, this paper focuses on age prediction for subjects from birth to two years of age using both sMRI and fMRI data.
However, considering the relatively low spatial resolution and high noise level of fMRI, as well as the immature and dramatically changing functional connectivity derived from it, it is infeasible or ineffective to directly fuse fMRI and sMRI data by conventional multimodal fusion strategies [10][16]. These strategies may even reduce the accuracy of only using features derived from sMRI, which have been verified as robust biomarkers for predicting infant age [17].
As one of the most popular model-based methods of multimodal data fusion, autoencoder (AE) [18] employs latent variables to achieve information combination. However, traditional autoencoders always mix shared information and complementary information from different modalities into a single latent variable, where the information from one modality may act as the noise obstructing the reconstruction of the other. Thus, the main challenge for an effective fusion of sMRI and fMRI data is to reduce the negative impact from one modality to the other in the fusion process. To address this problem, we propose a disentangled multimodal adversarial autoencoder (DMM-AAE) model to perform multimodal latent variable learning and age predictor building jointly. The key idea of this model is to disentangle the latent variable of each modality into common and specific codes to represent shared and complementary information of modalities separately. To realize the disentanglement, it requires that the common codes obtained from different modalities should be as similar as possible, while the specific codes differs from each other as much as possible. Thus, we define cross-reconstruction requirement enforcing each modality to be reconstructed by its own specific code and any common code of the modalities, which ensures the similarity of the common codes obtained from different modalities. Furthermore, the ratio of the distance between common codes to the distance between specific codes is defined and introduced to the model as common-specific distance ratio loss, which reinforces the difference between specific codes and the commonalities between common codes. Finally, the common codes and specific codes obtained from the two modalities are combined to predict age, and this process is integrated with latent representation learning as a unified framework. Moreover, to handle the missing modalities, the common and specific code of the existing modality is adopted to impute the latent variable of the missing modality iteratively. This imputation strategy is embedded into DMM-AAE, but can also be used as an independent algorithm for missing modality imputation.
In summary, 1) we built a deep DMM-AAE model using a latent variable disentanglement strategy to not only restrains the possible interference across the modalities effectively, but also acquires the fused information from sMRI and fMRI data; 2) we designed a cross-reconstruction requirement and a common-specific distance ratio as regularizations to guarantee the effectiveness of the disentanglement and the integrity of the combined information; 3) we integrated multimodal neuroimaging data fusion and age prediction into a unified framework to ensure learning age-related latent representation;4) we proposed an imputation algorithm for missing modality data by employing the shared information and specific information represented by the disentangled latent variable.
II. Related Work
A. Infant age prediction
There are two studies on predicting infant age with neuroimaging data. The first study involved subjects from 5 to 590 days of age [19]. It relied on features obtained by difference-of-Gaussian scale-space transformation of sMRI, which are less feasible on explaining the neurobiological changes of the infant brain. The other work [17] focused on subjects from birth to 2 years of age with sMRI. The scans in [17] were acquired at discrete time points (1, 3, 6, 9, 12, 18, and 24 months). This specific sampling strategy may introduce distortion on sample distribution and lead to bias when modeling a continuous mapping from brain MRI features to chronological age. Comparing to [19] and [17], our work 1) predicts infant age with multimodal neuroimages, i.e., sMRI and fMRI; 2) uses subjects with relatively continuous age distribution, thus leading to a model with higher generalization ability; 3) provides explainable multimodal biomarkers of infant brain development; 4) designs a new model for multimodal fusion, which can be generalized to other studies.
B. Multimodal data fusion
Available strategies for multimodal data fusion can be summarized in two categories: model-agnostic and model-based [20]. Model-agnostic fusion does not depend on a specific machine learning method and is usually classified into: early fusion and late fusion [18]. Early fusion is the most common approach to concatenate the features from different modalities as the input and followed by any regression model. Late fusion uses unimodal decision values and integrates them with certain fusion mechanisms, such as averaging, voting, or weighting [18]. Most of the multimodal neuroimaging-based age prediction researches employed such a model-agnostic fusion [10][16][21], which, however, cannot effectively exploit correlated information among multi-modalities. This issue turns us to model-based fusion that addresses modalities fusion through specific model construction. Amongst the model-based methods (e.g., multiple kernel learning, graphical model, and neural network [20]), autoencoder is one of the most popular multimodal data fusion models. It can also be categorized into early and late fusion strategies. The early fusion AE, as shown in Fig. 1(a), concatenates modality 1 and modality 2 to implement encoding and decoding, which mixes the information at the input stage. The late fusion AE is shown as Fig. 1(b), where each modality has its own encoder and decoder and the unimodal latent variables are concatenated together for reconstructing the two modalities and prediction. While being able to learn the complementary information, both early and late fusion AE do not distinguish complementary from shared information between the two modalities. If one modality contains heavy noise, the latent variable derived from it may obstruct accurate reconstruction and latent variable learning of the other modality. Different from these existing multimodal fusion method, Our model realizes fusion through disentangling and representing complementary and common information between two modalities.
Fig. 1.
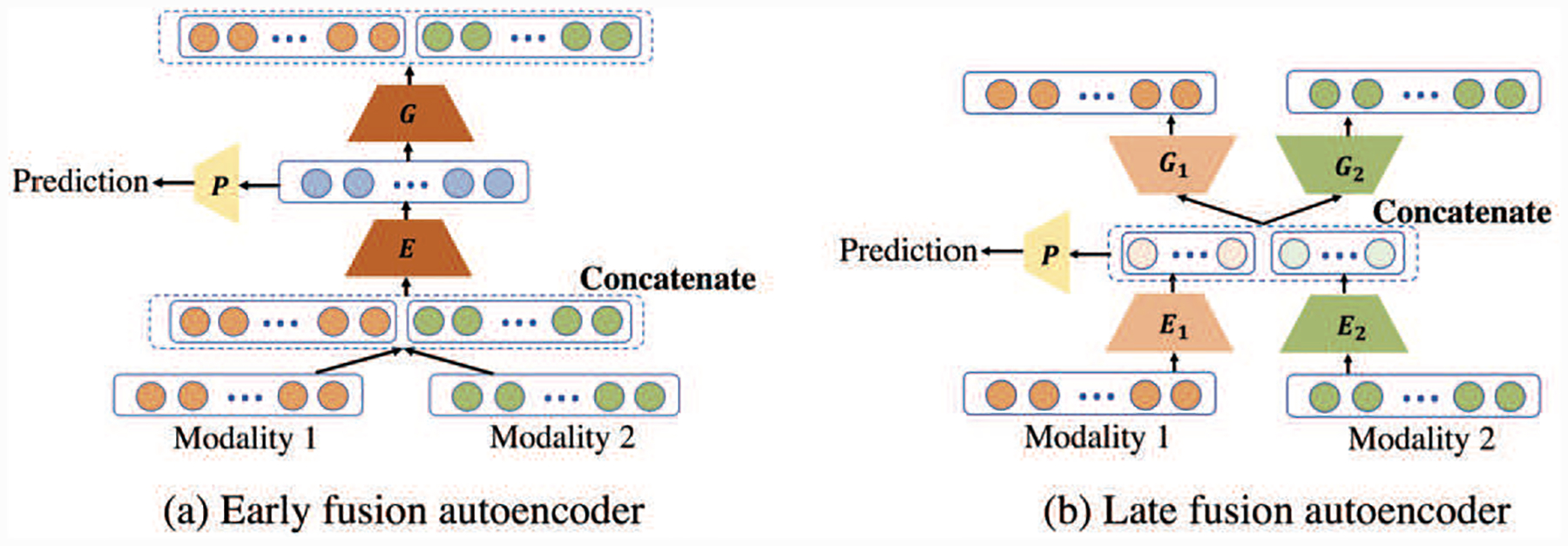
Different types of bimodal deep autoencoder (AE) for prediction with modalities fusion. (a) Early fusion AE: concatenating the features of modality 1 and modality 2 as a single input for the encoder, and the obtained latent variable will be used for prediction. (b) Late fusion AE: the modalities have their individual AEs while concatenating their latent variables together for prediction. E, E1, and E2 are encoders. G, G1, and G2 are decoders. P is a predictor.
C. Disentangled representation learning
Disentangled representation is a technique that encodes features into factors with separate meanings. The generative models for disentangled representation learning have shown great promise in the field of computer vision [22]. Semi-supervised disentangling approaches require explicit knowledge about the underlying factors and real factor label as guidance [23], which have superior performance but suffer difficulties in practical implementation. Unsupervised disentangling approaches take variational autoencoder (VAE) framework as the mainstream and learn disentangled representations by using extra penalties on the Kullback-Leibler (KL) divergence between the variational posterior and the prior [24]. Although VAE-based disentangled representation learning is effective, it aims to decompose the features into independent factors, which does not fit our requirement for representing shared and complementary information among modalities. Disentangling the latent variable by assigning specific meanings to decomposed factors is another kind of disentangled representation learning. The study in [25] belongs to such type and is most relevant to our work, which proposed an autoencoder model to explore the shared content and unique content of two domains. Our DMM-AAE model differs from [25] in three aspects. 1) The goals and the represented information by the disentanglement are totally different. The work in [25] focuses on image to image translation and emphasizes on removing the specific content of the first domain while importing the specific content of the second domain. Thus, shared content and unique content described in [25] are domain-based. However, our study focuses on individualized multimodal fusion, the shared and complementary information we modeled are subject-specific. 2) The characteristics of the respectively concerned data lead to different architectures of the autoencoder in [25] and our study. 3) The constraints designed to ensure the disentanglement are totally different. Compared with Zero loss and adversarial loss in [25], common-specific distance ratio loss and cross-reconstruction loss designed in our model are subject-based and better for multimodal fusion.
III. Materials
We verified the effectiveness of our proposed DMM-AAE model on infant age prediction using a high-quality MRI dataset from the UNC/UMN Baby Connectome Project [26]. We used 178 term born subjects with 326 structural MRI scans and 171 functional MRI scans acquired at different ages ranging from 35 to 848 days. The demographic information of these scans is illustrated in Table I.
TABLE I.
Subject demographics (M: month; the distribution of Age is represented by Mean±Standard Deviation)
| <3M | 3~6M | 6~9M | 9~12M | 12~18M | 18~24M | >24M | |
|---|---|---|---|---|---|---|---|
| Scans (Male) | 20 (11) | 44 (24) | 42 (17) | 60 (25) | 89 (44) | 35 (15) | 36 (22) |
| Age (days) | 60± 9 | 137± 27 | 215± 27 | 314± 29 | 438± 50 | 630± 52 | 767± 30 |
T1-weighted images were acquired with the following parameters: 208 sagittal slices, TR/TE = 2400/2.24 ms, acquisition matrix = 320 × 320, and resolution = 0.8 × 0.8 × 0.8 mm3. T2-weighted images were acquired with the following parameters: 208 sagittal slices, TR/TE = 3200/564 ms, acquisition matrix = 320 × 320, and resolution = 0.8 × 0.8 × 0.8 mm3. All structural images were preprocessed by a well-established infant-dedicated computational pipeline [27][28][29], including co-registration, intensity inhomogeneity correction, skull stripping, cerebellum removal, tissue segmentation, hemispheres separation, topological correction, and inner/middle/outer surface reconstruction. Each individual cortical surface was parcellated into 360 regions of interest (ROIs) [30] by aligning them onto the UNC 4D Infant Cortical Surface Atlas (https://www.nitrc.org/projects/infantsurfatlas/) [31]. Four types of morphological features, i.e., local gyrification index (LGI), average convexity, mean curvature, and cortical thickness, were obtained by averaging the corresponding values of all vertices inside each ROI. Other two types of features, i.e., surface area and cortical volume, were obtained by summing up the corresponding values over all vertices inside each ROI. High-resolution resting-state fMRI data (rs-fMRI, temporal resolution = 0.8s, and spatial resolution = 2 mm isotropic) were acquired during natural sleeping. Besides the traditional processing steps in the Human Connectome Project pipeline, we especially used the following strategies.(1) One-time re-sampling and denoising of functional signals were completed in the native image space. This approach avoids interpolation and smoothing of functional signals for multiple times, which typically cause ambiguities in capturing detailed functional patterns. (2)Deep learning-based noisy component removal for fast and robust fMRI denoising. All fMRI time series of vertices on the middle surface were extracted. After that, the same 360 ROIs were chosen to construct the functional connectivity map by calculating the Pearson’s correlation coefficient between time series of each pair of ROIs. Fishers r-to-z transformation was conducted to improve the normality of the functional connectivity.
IV. Method
A. Disentangled-Multimodal Adversarial autoencoder
The framework of DMM-AAE is depicted in Fig. 2 and detailed below.
Fig. 2.
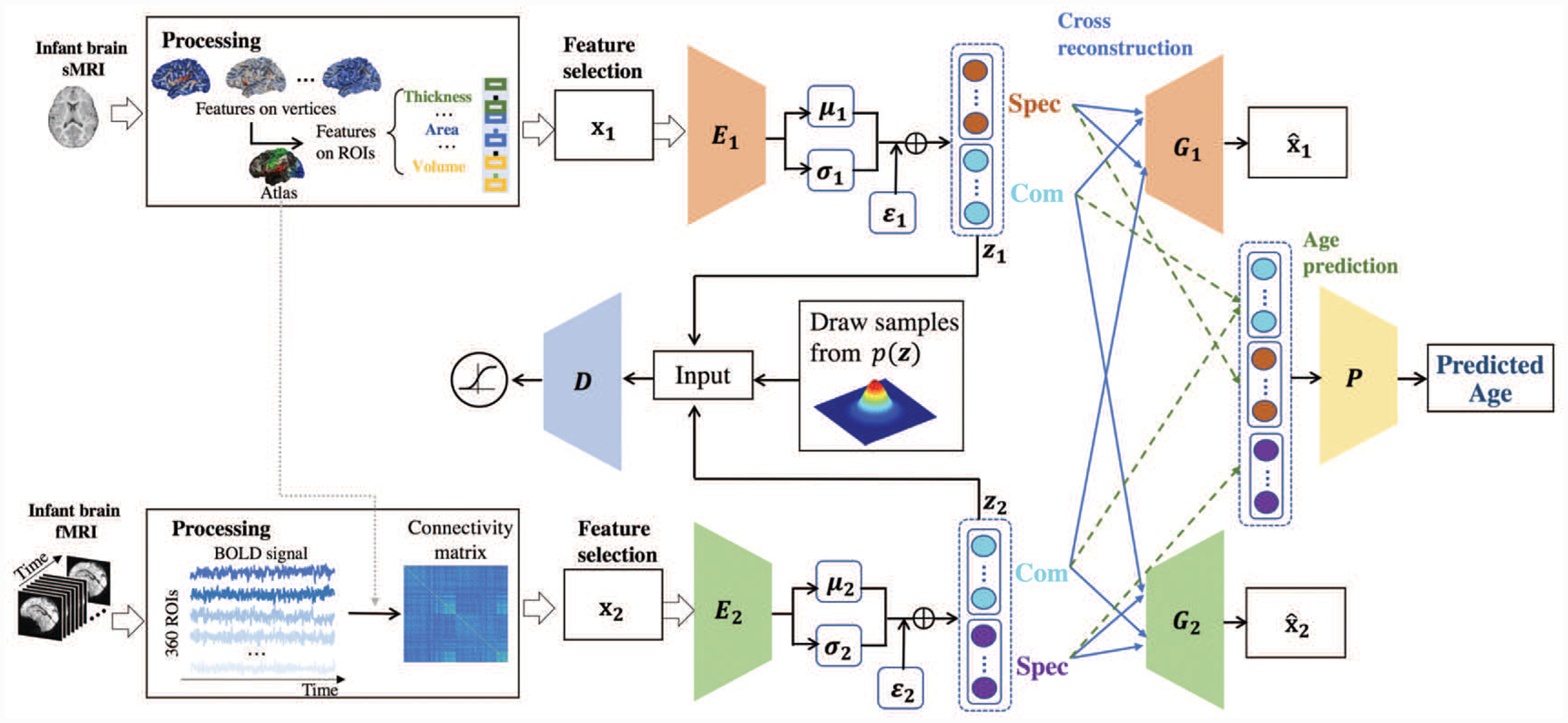
The framework of the proposed method: DMM-AAE.
Feature selection.
For a small dataset in practice, the dimension of 2,160 structural features (6 types of features on 360 ROIs) and 64,620 functional features (upper triangle elements of the 360×360 functional connectivity matrix) is extremely high, which is inefficient for training and vulnerable to overfitting. Thus, feature selection is requisite before the training of a neural network model. Based on their relationship with the induction model, feature selection methods can be distinguished into filter methods, wrapper methods, and embedded methods [32]. Since filter method is independent of the induction algorithm and generally much faster, it is chosen as our feature selection strategy. Herein, random forest is chosen as the feature selection method due to its superior performance on feature selection even for highly correlated high-dimensional data [33]. After feature selection, m1 and m2 features of the two modalities are selected for prediction, respectively. Our data appear as (X1, X2, Y) = {(x11, x21, y1), …, (x1n, x2n, yn), …, (x1N, x2N, yN))}, and are the n-th feature vector of the first modality and the second modality, respectively; is the corresponding output value (in our study, age). N is the number of instances.
Encoding.
For each modality, we employ a multi-layer perceptron neural network as its respective encoder Ei. The output of the encoder is called the latent variable, denoted as zin, i = 1, 2, n = 1, 2, …, N. Index n will be omitted when we are referring to terms associated with a single data point.
Latent variable disentanglement.
Ei generates the latent vector zi conditioned on the input feature vector of ith modality, zi = Ei(xi). To better learn the combined information from the two modalities, shared and complementary information should be separated. Here, zi is disentangled into two parts: Com(zi) and Spec(zi). Com(zi) is the common code representing the shared information amongst modalities, while Spec(zi) is the specific code representing the complementary information that differentiates one modality from the other. The basic requirements of the disentanglement are:
The concatenation of Com(zi) and Spec(zi) equals zi;
Com(z1) and Com(z2) should be as similar as possible;
Spec(z1) differs from Spec(z2) as much as possible.
Cross reconstruction.
For each modality, we employ a multi-layer perceptron neural network as its respective decoder Gi. Conventionally, since zi = [Com(zi), Spec(zi)] is the latent variable for xi, a direct requirement is the reconstruction of xi from zi, which signifies the similarity between the original input xi and the consequent reconstruction obtained by Gi(Com(zi), Spec(zi)). On the other side, since Com(zi) is the shared information among modalities, it should also provide information to reconstruct the other modality. Thus, to further elevate the effectiveness of the disentanglement, we introduce a cross-modality reconstruction requirement: each Spec(zi) is enforced to reconstruct xi together with any of the Com(zj), i, j = 1, 2. That is, the similarity of xi and Gi(Com(zj), Spec(zi)) is also required.
Age prediction.
Since the latent variable of each modality has been disentangled into the common code Com(Ei(xi)) and the specific code Spec(Ei(xi)), the combined information is formed as M(x1, x2),
where , μi determines the ratio of the combined common code from the two unimodal common codes. ω1 = ω2 = 0.5 in our experiment. A multi-layer perceptron neural network is then designed as a regressor P to predict infant age from M(x1, x2).
In our method, the two modalities employ their respective Adversarial autoencoder (AAE) [34] to isolate any possible interference and adopt disentanglement under cross-reconstruction requirement to realize information fusion. As an important element in AAE, a multi-layer perceptron neural network is taken as the shared discriminator D to impose the adversarial regularization on the latent vector zi, which tries to distinguish if zi follows a preassigned prior distribution. Ei, Gi, D, and P are all parameterized with weights and learned together with the following losses.
Adversarial loss.
Let p(zi) be the prior distribution imposing on the latent variable, q(zi|xi) be the encoding distribution and p(xi|zi) be the decoding distribution. AAE is a generative model that learns the data distribution pd(xi) by training an autoencoder with regularized latent space, which requires the aggregated posterior distribution q(zi) = ∫xi q(zi|xi)pd(xi)dxi matching the predefined prior p(zi). This regularization on the latent space is realized by an adversarial procedure with the discriminator D, which leads to a minEi maxD problem, where
| (1) |
The whole adversarial loss is the sum of the individual adversarial losses from the two modalities,
| (2) |
The encoder ensures the aggregated posterior distribution fool the discriminative adversarial network D into thinking that the latent vector zi comes from the prior distribution of latent vector p(zi), while D tries to distinguish between q(zi) and p(zi). Although p(zi) could be an arbitrary prior, a traditional Gaussian prior distribution was imposed on the latent variable zi in this study, i.e., p(zi) = N (zi|μi(xi), σi(xi)). The same re-parameterization trick in [35] was also used for back-propagation through the encoder network. Since Gaussian prior distribution is chosen for the latent variable of the two different modalities, they share the same discriminator D.
Except AAE, VAE is also capable of imposing prior distribution on the latent variable. VAE uses KL divergence penalty to enforce the aggregated posterior of the latent variable to simulate the prior distribution, while AAE uses an adversarial discriminator to do so. Compare with VAE, AAE may be superior on capturing the data manifold and imposing complicated prior distribution without exact functional form. AAE is possibly more general in various application scenarios. Thus, in our work, AAE is chosen to impose a prior distribution on the latent variable.
Common-specific distance ratio loss.
is defined following the basic requirements of latent variable disentanglement:
| (3) |
| (4) |
| (5) |
Regression loss.
L2 norm is adopted as our regression loss:
| (6) |
Reconstruction loss.
The reconstruction loss is defined based on the cross-reconstruction requirement. Since the neuroimage data can be incomplete, the reconstruction loss will not be calculated from the missing data.
| (7) |
Full Objective.
Finally, the objective functions to optimize Ei, Gi, D, and P are written as:
| (8) |
| (9) |
where λ1, λ2, and λ3 were trade-off parameters, and . The whole model together with the regularizations is named as a disentangled-multimodal adversarial autoencoder (DMM-AAE). DMM-AAE first updates its discriminative network D to tell apart the true samples (generated using the prior) from the generated samples (the latent vector computed by the encoder Ei) with , and then updates its encoder Ei, decoder Gi, and predictor P with , i = 1, 2.
B. Data Imputation for Missing Modality
Our DMM-AAE is also capable of working in the missing modality scenario. When the multimodal data are incomplete, DMM-AAE can impute the missing modality by an embedded strategy described below. Supposing that modality M1 is missing for some instances, Comi and Speci are the common code and specific code of Mi, i = 1, 2. Com2 = Com(E2(x2)) can be directly used to impute Com1, because the objective of the training is to maximize the similarity between the common codes obtained from the two modalities. A time index is introduced into the imputation, which serves as the variable to adjust the involvement of Spec2 into the imputation of Spec1. At the early stage of training, Spec2 = Spec(E2(x2)) is taken as the source of subject-specific information for the missing modality and is used as the major source for the imputation of Spec1. As the training going on, when the decoder of the modality 1, G1, can generate more reliable reconstructed data, Spec2 will be less involved in the imputation. In the training of DMM-AAE, the time index t can be chosen as the training epoch index and changes along with the training epoch of DMM-AAE, i.e., t0 = 1, and MaxIter equals to the number of training epochs of DMM-AAE. In the test stage, t0 is always set as a fixed value, like 100 in our experiment, and in step 6 is the final imputed value without further iteration, i.e., MaxIter = t0. Thus, during the testing process, Spec2 is only kept at a small portion to preserve some subject-specific information. The imputation process is depicted in Fig. 3 and also detailed in Algorithm 1.
Fig. 3.
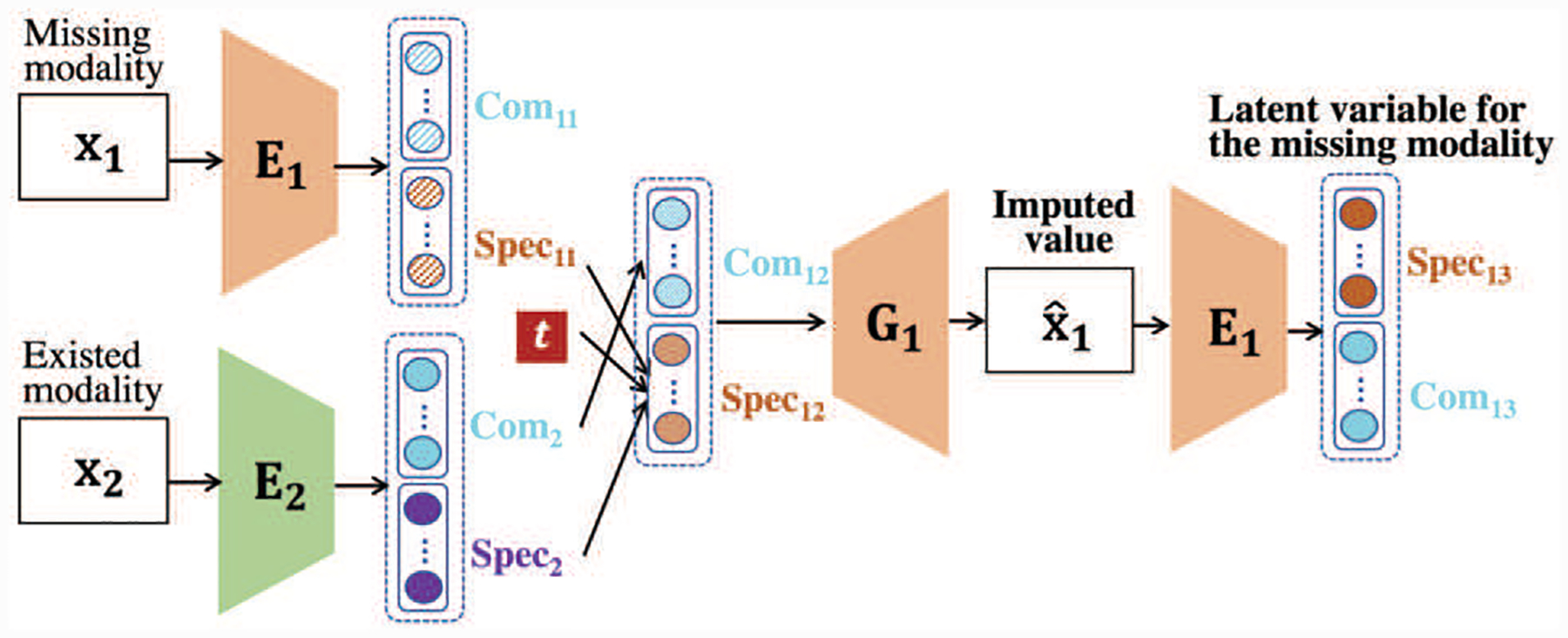
The imputation process of the missing modality.

C. Evaluation of Age Prediction
To evaluate the effectiveness of the proposed DMM-AAE model and analyze the relative importance of the features, a nested 10-fold cross validation was implemented 20 times. The trade-off parameters in the loss function defined in Eq. (9) were optimized from the inner cross validation by minimizing the mean absolute error (MAE) of the prediction with the range of λ1 ∈ {0.04, 0.05, 0.06}, λ2 ∈ {2, 4}, and λ3 ∈ {0.02, 0.03}. The ranges were determined by empirical results, which can be found in the supplementary material. The prediction results were evaluated by the outer cross validation to remain the training stage blind to the testing data. During the cross validation, for the longitudinal scans from the same subject, we guaranteed that the scans in the training data were acquired in earlier ages than those in the testing data. The age prediction model was assessed by three metrics, i.e., MAE, mean relative absolute error (MRAE), and the correlation coefficient (r) between the predicted ages and the chronological ages. Of note, MRAE is the mean of the absolute error divided by the corresponding chronological age and expressed in terms of percentage. For r, the 95% confidence interval was computed by the 2.5 and 97.5 percentiles of correlation values obtained from a bootstrap method with 1,000 samples. The same bootstrap samples were adopted for the 20 times of 10-fold cross validation when computing the confidence interval of r, which guarantees the bootstrapping is not biased to any certain cross validation.
D. Analysis of Features Importance in Age Prediction
The most contributive features for age prediction could be regarded as the infant brain development biomarkers. In our proposed model, RF selects feature subsets for prediction in a process independent of the chosen predictor. Thus, the importance analysis of the features consists of two parts: the frequency of being selected by RF and the permutation importance in the DMM-AAE neural network.
1). Selection frequency by RF:
As the feature selection method, RF estimates the importance of the features by outof-bag (OOB) estimates [33]. To evaluate the importance of each variable, the values of each variable in the OOB samples are allowed to permute. The difference between the accuracies of the original and perturbed OOB samples over all trees in RF are averaged as importance estimation. In each fold, a RF model will be trained, and the importance of each feature will be estimated on the training set. Then, the feature with an estimated importance higher than the threshold (setting as 10−6 in our experiment after some empirical tests) is selected to train the DMM-AAE model, which will be used for age prediction in the testing data of this fold. The frequency of each feature being selected in the 20 times 10-fold cross validation iterations represents the relative importance of the features. A morphological feature and a functional connectivity feature are regarded as the contributive features if their selection frequencies are higher than 90% and 50%, respectively. The different frequency thresholds set for the importance analysis of a morphological feature and a functional connectivity feature are based on the different distribution of their selection frequencies, which is shown in Fig. 7(a).
Fig. 7.
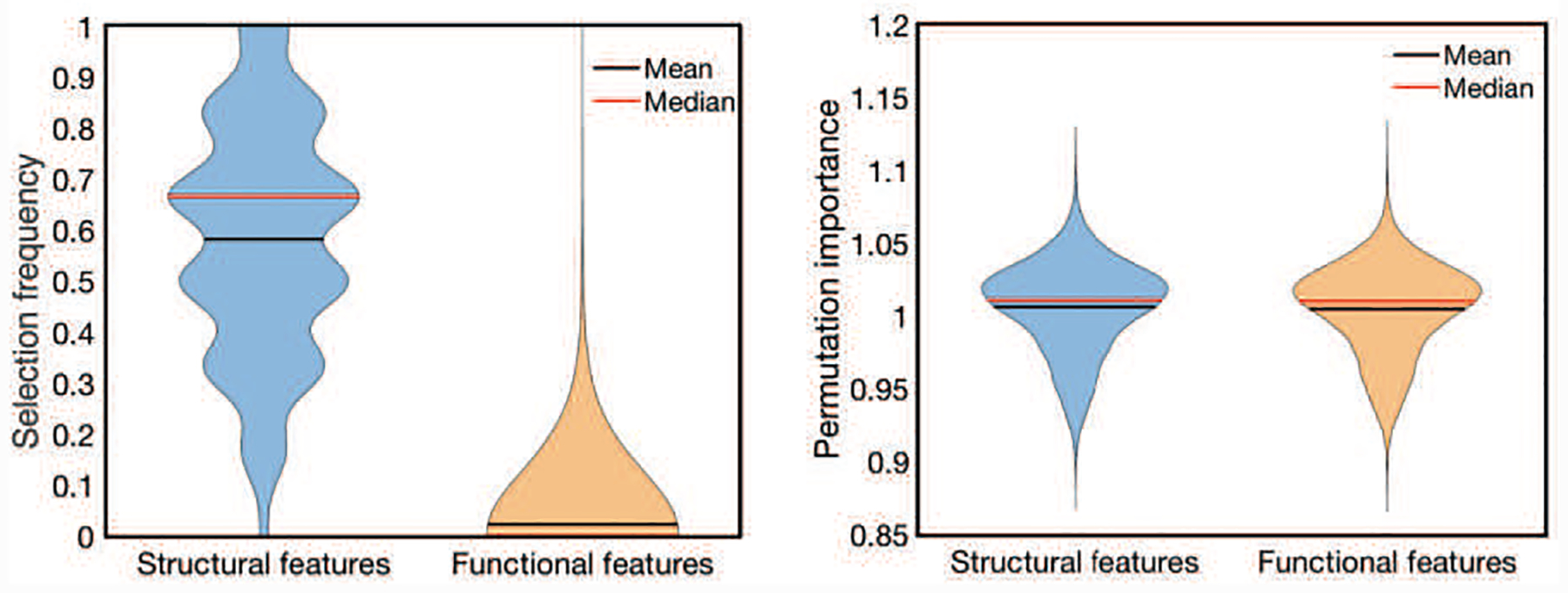
(a) The distribution of the feature’s selection frequency and (b) The distribution of the permutation importance of the selected features.
2). Permutation importance with DMM-AAE:
Based on a well-trained DMM-AAE model, permutation importance [36] was used for measuring the contribution of each feature to age prediction due to its simplicity of being model agnostic. The permutation importance (PI) of a feature f is defined as
| (10) |
where Errororig and Errorperm are the prediction errors (evaluated by MAE in our study) based on the original data set and the new data set with the values of feature f shuffled. Shuffling the feature f means randomly reorganize the order of the values of f in the data set with other features fixed. Since this procedure breaks the relationship between f and the age, the increase of the model error is indicative of the dependency of the model on the feature. As a result, the feature f is “important” if shuffling its values leads to PI(f) > 1.
In each fold, the permutation importance of every selected feature was measured by equation (10) on the testing data and repeated five times. Thus, 1000 PI values were obtained for each feature after 20 times of 10-fold cross validation. A one-tailed one-sample t-test was implemented on the 1000 PI values to determine if the mean PI value of each feature is significantly bigger than 1. The threshold was chosen as p < 0.05 after Bonferroni correction (i.e., the uncorrected p < 0.05/66780) [37].
V. Results
A. Comparison with the State-of-the-art Methods
We compared the proposed DMM-AAE model with seven model-agnostic, two model-based, and two AAE-based multimodal regression methods: 1) random forest (RF (Early)), where “Early” means early fusion that concatenates sMRI and fMRI features into a vector as input; 2) Support vector regression (SVR (Early)); 3) Gaussian process regression (GPR (Early)); 4) Partial least squares regression (PLSR (Early)); 5) PLSR (Late 1), where “Late 1” means that the unimodal predicted ages based on PLSR models are fused by a GPR model;6) PLSR (Late 2), where “Late 2” means that the unimodal predicted ages based on PLSR models are fused by average;7) PLSR (Hybrid), where “Hybrid” means that predicted ages obtained from PLSR (Early) and PLSR (Late 1) are fused with average mechanism; 8) multiple kernel learning (MKL) [38], where two different kernels are respectively implemented on sMRI features and fMRI features before an optimal combined kernel is learnt for regression; 9) Incomplete Multi-Source Fusion (iMSF) [39], which divides samples according to the availability of data sources and learns shared sets of features with sparse regression; 10) Adversarial autoencoder (AAE (Early)), where sMRI and fMRI features are concatenated as the input of the encoder and the latent variable is used for age prediction; 11) Adversarial autoencoder with latent variable fusion (AAE (Late)), where unimodal latent variables are pooled together for age prediction. To keep the comparison fair, we integrate the multimodal fusion and age prediction into a unified framework for the AAE (Early) and AAE (Late), as same as the design of DMM-AAE. The values of the missing modality were completed by zero-imputation.
The architecture of the DMM-AAE used in our experiments is shown in Fig. 4. DMM-AAE was implemented with Pytorch and optimized with Adamax by a fixed learning rate of 0.001. The batch size was set as 150. The dimension of the latent variable was 120, while the dimensions of common code and specific code were set as 50 and 70, respectively. The dimension of the latent space, common code, and specific code were set based on some empirical tests. How the setting of these dimensions affects the final prediction accuracy can be found in the supplementary material. AAE (Early) and AAE (Late) share the same architecture as DMM-AAE for the fairness of the comparison.
Fig. 4.
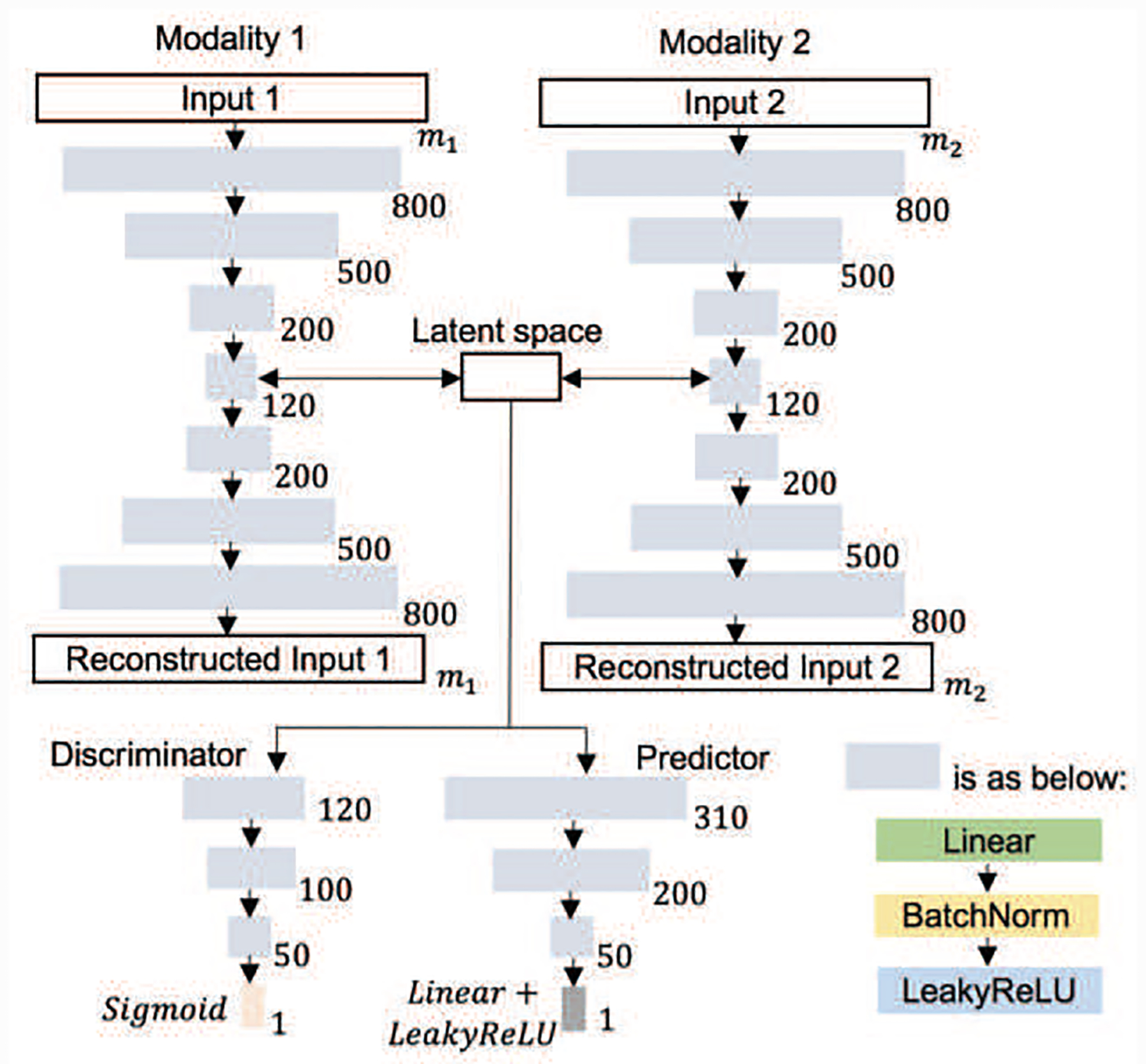
The architecture of the DMM-AAE used in our experiments.
The comparison results are summarized in Table II. Scatter plots of the predicted ages against the chronological ages are shown in Fig. 5 based on four representative methods: SVR (Early), AAE (Late), MKL, and DMM-AAE.
TABLE II.
The comparison among DMM-AAE and some mult-modal regression methods (The performances are shown by Mean±Standard Deviation and the best one is in bold font)
| Fusion type | MAE (days) | MRAE | rL | rR |
|---|---|---|---|---|
| Model-agnostic | ||||
| RF (Early) | 56.2±0.8 | 0.17±0.003 | 0.904±0.004 | 0.943±0.002 |
| SVR (Early) | 54.1±1.5 | 0.21±0.007 | 0.931±0.003 | 0.954±0.002 |
| GPR (Early) | 69.7±0.6 | 0.23±0.002 | 0.895±0.002 | 0.925±0.001 |
| PLSR (Early) | 53.6±1.4 | 0.20±0.007 | 0.932±0.003 | 0.954±0.002 |
| PLSR (Late 1) | 50.3±0.7 | 0.19±0.005 | 0.935±0.005 | 0.956±0.004 |
| PLSR (Late 2) | 78.5±0.9 | 0.34±0.009 | 0.921±0.021 | 0.943±0.018 |
| PLSR (Hybrid) | 50.9±0.7 | 0.19±0.006 | 0.932±0.005 | 0.956±0.003 |
| Model-based | ||||
| MKL | 49.1±1.3 | 0.17±0.008 | 0.935±0.003 | 0.959±0.002 |
| iMSF | 59.6±1.2 | 0.21±0.007 | 0.916±0.003 | 0.943±0.002 |
| AAE-based | ||||
| AAE (Early) | 43.0±1.7 | 0.15±0.009 | 0.944±0.004 | 0.968±0.003 |
| AAE (Late) | 43.8±1.8 | 0.15±0.010 | 0.949±0.005 | 0.965±0.003 |
| DMM-AAE | 37.6±1.3 | 0.11±0.004 | 0.953±0.003 | 0.975±0.002 |
Fig. 5.

The scatter plots of the predicted ages and chronological ages based on DMM-AAE, PLSR (Early), MKL, and AAE (Late).
Model-agnostic fusion and traditional model-based fusion perform similarly on age prediction. The MAE obtained by the nine methods ranged from 50.9 to 78.5 days; the MRAE is around 19% to 34%; and the average correlation r ranged from 0.932 to 0.944. AAE-based methods showed improved performance, which reveals the benefit from the age-related latent variable learning. Our model DMM-AAE outperforms all the baseline methods by reducing the MAE and MRAE to37.6 days and 11%, respectively, while increasing the midpoint of the 95% confidence interval of r to 0.964.
The performance of PLSR varies with the fusion type. There is a 24.9 days difference in MAE between PLSR (Early) and PLSR (Late 2). Since “Late 2” means that the unimodal predicted ages based on PLSR models are fused by average, it can be inferred that the worse performance of PLSR (Late2) compared with PLSR (Early) could come from the bad performance of fMRI data, due to the high noises in fMRI.
To further show the detailed prediction performance, the evaluation based on MAE from DMM-AAE and all the competing methods were broken down into different age periods and shown in Table III. These methods perform differently at different age periods, especially in the age periods within the first year after birth. SVR (Early) performs consistently in all age periods of the first two years and turns as the best regressor at the time period of “18~24M”. Except “18~24M”, DMM-AAE always leads to better performance on all the age periods. In particular, the superiority of our proposed DMM-AAE is more obvious in the first two time periods: “<3M” and “3~6M”. DMM-AAE respectively reduces the MAE at “<3M” and “3~6M” to 19.1 and 20.9 days, while the average MAE of other methods at these two time points are 44.6 days and 39.3 days, respectively. It can be found that the prediction error obtained by DMM-AAE is getting bigger along the time, especially at the age periods after 1 year old. This prediction error pattern is possibly due to a relatively stationary brain structural development [17], higher individual variability, and more vulnerable to environmental influences during the second year, which makes the distinguishability of the brain age harder.
TABLE III.
The broken-down MAE (days, Mean±Standard Deviation) obtained from DMM-AAE and some baseline methods (M: Month; best performance at each time period is in bold font.)
| Fusion type | <3M | 3~6M | 6~9M | 9~12M | 12~18M | 18~24M | >24M | 0~12M | 12M~24M |
|---|---|---|---|---|---|---|---|---|---|
| Model-agnostic | |||||||||
| RF (Early) | 31.2±2.5 | 21.3±1.7 | 21.3±1.5 | 53.1±2.1 | 59.2±2.2 | 79.4±4.3 | 131.1±5.2 | 33.5±1.0 | 65.0±1.9 |
| SVR (Early) | 49.0±4.3 | 44.8±2.7 | 43.0±2.7 | 52.4±3.8 | 55.1±2.7 | 57.7±3.0 | 78.2±3.7 | 47.6±1.8 | 55.8±1.8 |
| GPR (Early) | 36.0±1.4 | 44.0±1.4 | 49.0±1.1 | 67.6±1.0 | 54.2±1.0 | 94.3±0.9 | 161.3±1.5 | 52.9±0.7 | 65.5±0.9 |
| PLSR (Early) | 38.9±3.3 | 41.0±2.5 | 40.0±2.5 | 52.1±2.6 | 51.4±2.2 | 64.3±2.3 | 90.8±2.5 | 44.5±2.0 | 55.0±1.7 |
| PLSR (Late 1) | 39.6±4.7 | 41.1±2.8 | 37.9±2.6 | 48.8±3.1 | 45.7±2.0 | 63.5±1.3 | 82.6±2.5 | 42.9±1.5 | 50.7±1.2 |
| PLSR (Late 2) | 114.6±6.0 | 76.9±2.4 | 63.2±1.3 | 53.3±2.8 | 42.5±1.5 | 108.7±1.4 | 175±2.5 | 69.4±1.8 | 58.8±0.8 |
| PLSR (Hybrid) | 39.2±4.3 | 39.5±2.7 | 38.2±2.5 | 50.3±3.2 | 46.6±2.0 | 64.3±1.6 | 80.1±2.3 | 43.2±1.7 | 50.9±1.5 |
| Model-based | |||||||||
| MKL | 39.7±7.1 | 34.9±3.6 | 27.0±2.6 | 37.8±3.0 | 52.6±2.6 | 71.8±6.3 | 88.1±5.3 | 34.6±1.8 | 58.0±2.4 |
| iMSF | 43.1±4.4 | 44.1±2.3 | 41.7±3.3 | 53.9±3.2 | 52.8±2.2 | 65.8±3.6 | 125.3±6.4 | 46.9±1.7 | 56.5±1.7 |
| AAE-based | |||||||||
| AAE (Early) | 25.9±5.2 | 21.4±1.7 | 25.9±2.8 | 40.2±2.2 | 43.8±2.3 | 68.3±5.1 | 76.2±5.5 | 29.6±1.3 | 51.7±2.0 |
| AAE (Late) | 33.0±7.7 | 23.4±2.3 | 31.0±2.4 | 41.6±2.3 | 43.5±2.9 | 63.9±4.2 | 74.4±5.1 | 33.0±1.5 | 49.3±2.1 |
| DMM-AAE | 19.1±2.5 | 20.9±1.7 | 21.1±1.4 | 30.3±2.3 | 42.3±3.1 | 64.5±4.0 | 61.4±4.3 | 24.2±1.1 | 48.6±1.9 |
B. Comparison between multi-modality and uni-modality
To analyze the effect of multi-modality fusion, Fig. 6 shows the performance comparison of different models using unimodal (i.e., sMRI or fMRI) and multimodal data (i.e., sMRI+fMRI). For the multimodal regression methods PLSR (Early), PLSR (Late 1), PLSR (Late 2), and PLSR (Hybrid), their corresponding unimodal regression models are the same, i.e., the original unimodal PLSR. The corresponding unimodal regression model for DDM-AAE is the classical AAE because the disentanglement strategy, cross-construction loss, and common-specific distance ratio loss are all disabled when there is only one modality. Therefore, the unimodal regression modal compared with DDM-AAE, AAE (Early), and AAE (Late) are the same. From Fig. 6, the MAEs of the prediction obtained from sMRI alone are around 42.4~70.8 days, while those obtained by fMRI data are as big as 75.4~110.7 days. With SVR, PLSR (Early), PLSR (Late 2), AAE (Early), and AAE (Late), sMRI+fMRI obtain lower accuracy than sMRI. Even with RF (Early), GPR (Early), PLSR (Late 1), and PLSR (Hybrid), sMRI+fMRI only get a little improvement on the performance comparing with using sMRI data only. It shows that, in conventional multimodal fusion methods, fMRI data tend to introduce more noises than useful signals into the age prediction and lead to lower accuracy than that merely using sMRI data. With DMM-AAE, the MAE obtained by sMRI data is reduced from 42.4 to 37.6 days.
Fig. 6.
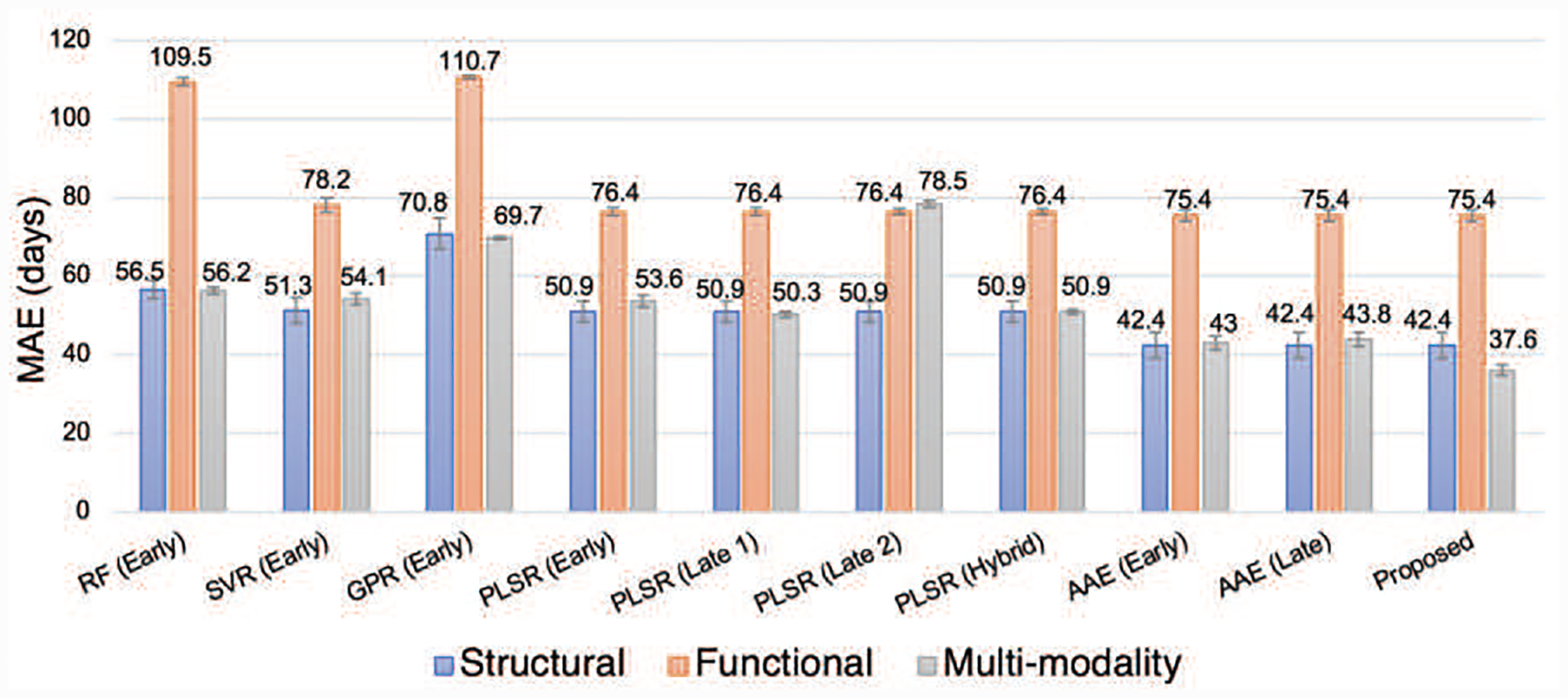
The comparison between multimodal methods and unimodal methods.
C. Comparison related to imputing the missing modality
Imputation is a class of procedures that aims to fill in the missing values with estimated ones. We verify the advantage of our proposed Algorithm 1, as an independent imputation method, for missing modality completion by comparison with the following state-of-the-art methods
Zero imputation. The missing values are filled with zeros. Since all the features are normalized as z-score (i.e., subtract the mean and divide by the standard deviation) before the imputation process, this method is equivalent to filling the missing feature values with average of the observed values.
k-nearest neighbor (KNN) imputation [40]. The missing values are filled with a weighted mean of the k nearest-neighbor samples, where the weights are determined by the mean squared difference from the neighboring samples. We set k = 3 after several empirical tests.
IterativeSVD [41]. The missing values are filled with the linear combination of a set of mutually orthogonal expression patterns obtained by iterative low-rank SVD decomposition.
BiScaler [42]. Imputation of missing value is taken as the matrix completion problem and realized by cooperating nuclear-norm-regularized matrix approximation and maximum-margin matrix factorization. The related matrix factorization problem is solved by the fast alternating least squares algorithm.
Herein, KNN, IterativeSVD, and BiScaler were all implemented by Fancyimpute (https://pypi.org/project/fancyimpute/) with default parameter values. After missing modality imputation, PLSR was chosen as the age prediction method because of its superior performance compared to other regression algorithms (as shown in Table II). With 20 times of 10-fold cross validation implemented on the data, the comparison results of the age prediction based on five types of imputation and PLSR regression are shown in Table IV. Our proposed imputation algorithm outperforms other baseline methods, which further proves the effectiveness of disentangling the latent variables.
TABLE IV.
The comparison among DMM-AAE based imputation and some baseline methods (The performances are shown by Mean±Standard Deviation and the best one is in bold font)
| MAE (days) | MRAE | rL | rR | |
|---|---|---|---|---|
| Zero imputation | 53.6±1.4 | 0.20±0.007 | 0.932±0.003 | 0.954±0.002 |
| KNN | 52.1±0.7 | 0.18±0.006 | 0.933±0.002 | 0.955±0.001 |
| IterativeSVD | 55.6±0.9 | 0.20±0.008 | 0.930±0.002 | 0.953±0.002 |
| BiScaler | 55.4±1.0 | 0.19±0.006 | 0.931±0.002 | 0.952±0.001 |
| Proposed Algorithm 1 | 50.9±1.1 | 0.18±0.010 | 0.938±0.003 | 0.957±0.002 |
D. Importance analysis of the features
Fig. 7(a) shows the distribution of the features’ selection frequencies. For sMRI features, the mean of their selection frequencies is nearly 0.6. However, the mean selection frequency of the functional connectivity is as low as 0.02. Since sMRI and fMRI features were selected independently, the low selection frequency of functional connectivity does not result from the interference of sMRI data but its own instability. As for the permutation importance of the selected features shown in Fig. 7(b), there is no significant difference between the PI value distributions of structural features and functional connectivity features. The means of the PI values of structural features and functional connectivity features are similar and bigger than 1.
Fig. 8 summarizes the importance of the features and the most contributing ROIs from the viewpoints of morphology and functional connectivity. As for the selection frequency, the top 3 important morphological feature types are “cortical thickness”, “cortical volume”, and “surface area”. The most contributing ROIs induced from structural features are bilaterally distributed on the brain. “Cortical thickness” of the orbitofrontal cortex and temporopolar, and “surface area” of the prefrontal cortex and orbitofrontal cortex are 100% selected. Although the average selection frequency of functional connectivity features is as low as 0.02, two functional connections (one is between the left primary sensory cortex and the right inferior parietal cortex, the other is between right mid-cingulate cortex and right opercula) still get involved into predicting age with a high frequency of 90%. The importance of features is further discussed together with the permutation importance. From the perspective of morphology, the most contributing ROIs are those satisfying the requirements: 1) the selection frequency is higher than 90%; 2) the p-value of the one-tailed t-test for PI > 1 is smaller than 0.05 after Bonferroni correction. As shown in Fig. 8(a), the most contributing ROIs are the left area trigeminal ganglion dorsal, primary visual cortex, second visual area, right Orbitofrontal cortex, and left prefrontal cortex. From the functional perspective, the most contributing ROIs and functional connectivity features are those satisfy the requirements: 1) the selection frequency is higher than 50%; 2) PI > 1. The p-value of the one-tailed t-test for PI > 1 is not taken into consideration because all of the p-values obtained from function connectivity are bigger than 0.05 after Bonferroni correction. As shown in Fig. 8(b), the right opercular, right primary sensory cortex, right primary motor cortex, and bilateral mid-cingulate cortex are discovered as the most important ROIs.
Fig. 8.
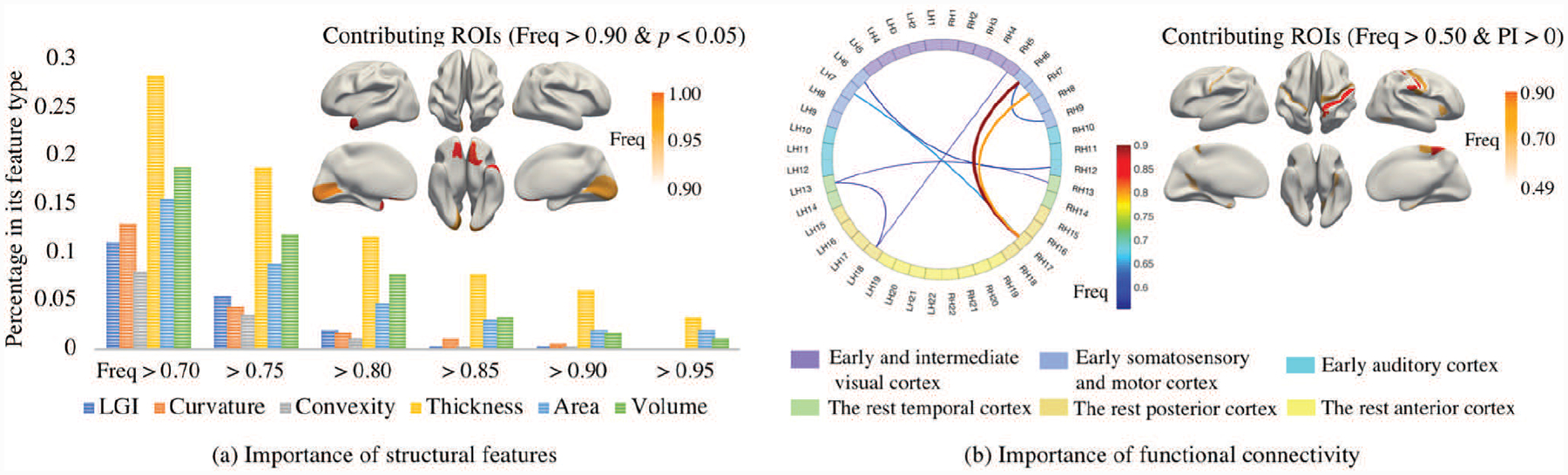
The importance of the features. The percentage of the features in its feature type with the selected frequency higher than the thresholds (0.7, 0.75, 0.80, 0.85, 0.90, and 0.95) are shown in (a) by grouped histograms. The morphological contributing ROIs that satisfy the requirements, 1) selection frequency is bigger than 0.90, and 2) the p-value of the test “PI>1” is smaller than 0.05, are shown in (a). The most contributing functional connectivity and ROIs that satisfy the requirements, 1) selection frequency is bigger than 0.50, and 2) its permutation importance bigger than 1, are shown in (b). For simplicity, of the connectivity figure in sub-figure (b), 180 ROIs on each brain hemisphere were grouped to 22 sections based on geographic proximity and functional similarities [30], where L and R represent left and right hemisphere, respectively. The functional connectivity between two sections was measured as the maximum of the connectivity between the related ROIs.
VI. Discussion
A. The performance of DMM-AAE on infant age prediction with incomplete multimodal neuroimages
1). The disentanglement of the latent variables solves the problem of possible noises introduced by fMRI data:
As the results shown in Fig. 6, using multimodal data does not always guarantee to outperform their counterparts using unimodal data only. Inappropriate fusion could lead to even worse performance compared to the model only using sMRI. Our proposed DMM-AAE arranges relatively independent autoencoders to separate the modalities and employs disentanglement under cross-reconstruction requirement to integrate them. With common codes building the connection between modalities and specific codes differentiating them, our DMM-AAE method effectively combines the information and restrains the possible interference between the modalities.
2). The disentanglement of the latent variable is ensured based on the proposed losses:
Fig. 10 shows how the losses change over iterations in the training and testing processes of DMM-AAE. It is shown that the common-similarity loss (the distance between common codes) decreases while the specific-similarity loss (the distance between specific codes) increases as expected, which suggests that the common codes of the two modalities become more similar while their specific codes increasingly differentiate each other over iterations. This result verifies the feasibility of common-specific ratio loss in administrating the disentanglement of the latent variable. The validity of the disentanglement is further ensured with the decreases of cross-reconstruction loss. Moreover, AAE (Late) is a version of DMM-AAE without both latent variable disentanglement and the restriction of common-specific ratio loss and cross-reconstruction loss. As shown in Table II, the fact that DMM-AAE outperforms the AAE (Late) demonstrates the superiority of the latent variable disentanglement and our new regularizations combined with it.
Fig. 10.
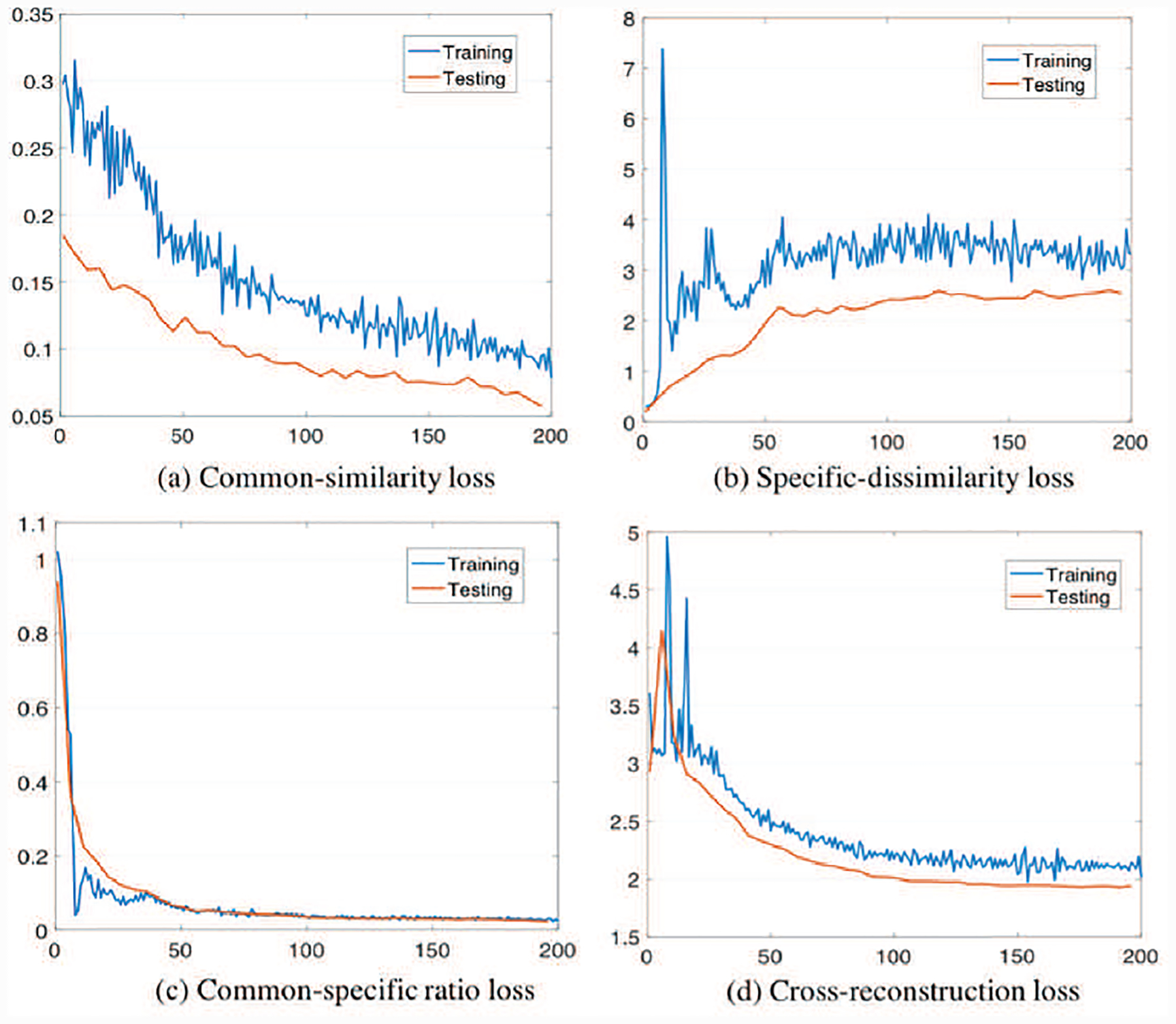
Losses over iterations in the training and testing processes of DMM-AAE.
3). The incompleteness of the multi-modality neuroimages is well handled by the imputation strategy embedded in DMM-AAE:
Since the missing modality imputation algorithm is embedded into DMM-AAE to handle the incomplete neuroimaging data, a comparison was implemented to show its effectiveness. The original dataset was divided into a complete part with no modality missing and an incomplete part with one modality missing. Then, the performances of age prediction obtained by AAE (Early), AAE (Late), and DMM-AAE were broken down into the complete and incomplete parts. The mean, standard deviation, and median of the absolute error on the two data parts were recorded and averaged on the 20 times of 10-fold cross validation. The comparison results are shown in Table V. For AAE (Early) and AAE (Late), the MAE on the incomplete data is four days larger than that on the complete data. However, the performance of DMM-AAE on the incomplete data is as well as, sometimes even better than, that of the complete data, which verifies that the imputation strategy embedded in DMM-AAE well handles the missing modality problem.
TABLE V.
The comparison of AAE (Early), AAE (Late), AND DMM-AAE on handling missing modality by separately calculating their prediction absolute error (days, Mean±Standard Deviation) on complete and incomplete parts of the original data
| Method | Mean | Standard Deviation | Median | |||
|---|---|---|---|---|---|---|
| Complete | Incomplete | Complete | Incomplete | Complete | Incomplete | |
| AAE (Early) | 41.1±1.1 | 46.2±1.7 | 36.5±2.7 | 48.2±3.6 | 26.7±0.7 | 31.3±2.3 |
| AAE (Late) | 43.9±0.9 | 47.9±2.1 | 35.6±2.3 | 46.4±3.1 | 35.6±1.5 | 36.7±2.9 |
| DMM-AAE | 39.2±0.5 | 36.3±0.7 | 36.3±1.8 | 40.3±2.8 | 26.8±0.3 | 25.3±1.9 |
To further analyze the imputed data based on DMM-AAE, we generated synthetic data set by randomly deleting 5% sMRI from the original data set. MRAE and RMSE (Root Mean Square Error) between the original and imputed features obtained from five times of 10-fold cross validation were reported in Table VI. It shows that DMM-AAE is still superior to the other four state-of-the-art methods on missing data imputation.
TABLE VI.
The comparison among DMM-AAE and the baseline methods on imputing data. MRAE and RMSE (mean±Standard Deviation) measure the distance between the original and imputed features
| Zero Imputation | IterativeSVD | BiScaler | DMM-AAE | |
|---|---|---|---|---|
| MRAE | 1.00±0.032 | 1.56±0.028 | 2.13±0.197 | 0.95±0.025 |
| RMSE | 0.956±0.004 | 0.998±0.004 | 1.040±0.006 | 0.677±0.001 |
4). Age-related latent variable is learned by integrating age prediction with latent variable learning:
As a popular unsupervised, non-linear technique used for visualizing high-dimensional data, t-distributed stochastic neighbor embedding (t-SNE) [43] intuitively shows how the data is arranged in a high-dimensional space and if it is well separated. In our study, since the multimodal neuroimaging data fusion and age prediction have been integrated into a unified framework, t-SNE was used to evaluate if the latent variable obtained by DMM-AAE is age-related. The original data and latent variables obtained by DMM-AAE or by DMM-AAE without age prediction module were visualized by using t-SNE (initialization = PCA, random-state = 500, perplexity = 5) and shown in Fig. 9. DMM-AAE without age prediction module means that the predictor is excluded from the basic model, and thus the age regression loss is removed from the full objective of DMM-AAE. It shows that the latent variables obtained by DMM-AAE are well arranged by age, while the ones obtained by DMM-AAE without embedding age prediction are scattered on the plot and totally age-irrelevant. Thus, DMM-AAE realizes the learning of age-related latent variables in the unified framework and has the potential to provide age-correlated brain development index.
Fig. 9.
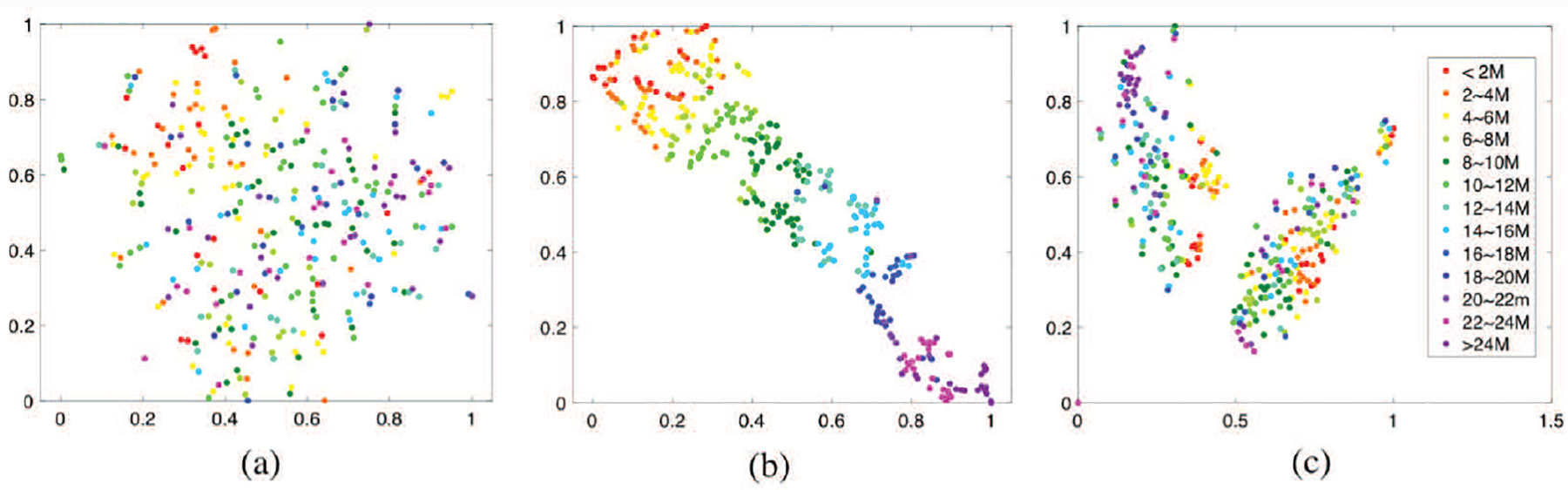
The t-SNE based visualization of (a) the latent variables obtained by DMM-AAE without age prediction module, (b) the latent variables obtained by DMM-AAE, and (c) the original feature set.
B. Important biomarkers of early brain development
1). Cortical thickness is identified as an important biomarker for brain development:
Cortical thickness is identified as an important biomarker for brain development: Six types of morphological features (LGI, average convexity, mean curvature, cortical thickness, surface area, and cortical volume) were included in the prediction model, while cortical thickness appears as the most important predictor for age prediction with the highest selection frequency. Because the thickness of the cerebral cortex in a given location likely reflect how cortical neurons are organized rather than simply indicating the density of gray matter tissue within a Cartesian search space, cortical thickness may offer more insights into how the brain structure is related to intelligence [44], normal development, aging, and brain disorders [45] than other measures. Our results further support the superiority of cortical thickness in brain development monitoring.
2). The discovery of the important ROIs and functional connections may reveal the brain development pattern in the first two years after birth:
In age prediction, the importance of early visual cortex represented by cortical thickness reveals its capability on distinguishing brain development status, which is consistent with the notable changes of the relative distribution of cortical thickness presented in the cuneus cortex (converting from a relatively thick region at birth to a relatively thin region at 1 year of age) and lingual gyrus (converting from a relatively thick region at birth to a nonsignificant region at 1 year of age) [46]. The most contributing morphology-related ROIs are bilaterally distributed on the brain, while rightward asymmetry is shown in the most contributing functional connectivity-related ROIs. This fact may indicate the difference lies in the structural and functional developmental trajectories at the early ages of the brain. Furthermore, the importance of the connections between the primary functional regions and high-order functional regions possibly specifies that the increasingly efficient connection between these areas may be significantly strengthened in the first two years.
C. Limitation and future work
Although AAE has been verified as an effective model for multimodal neuroimage fusion, some popular types of autoencoder, e.g., variational autoencoder (VAE), may be useful for our study. Especially the disentangled representation study of VAE [47], which tries to separate the latent units being sensitive to variations in different generative factors, has high potential to extend our current work. Furthermore, different parcellations of the brain, different features from sMRI (e.g., cortical myelination, T1 white/gray contrast), different functional features (e.g., amplitude of low frequency fluctuations, regional homogeneity), and more modalities (e.g., diffusion MRI) can be considered to boost the accuracy of infant age prediction. Moreover, the main framework of our proposed DMM-AAE focuses on the fusion of two modalities. Although it is not difficult to generalize the concepts of common code and specific code to three or more modalities, more specific designs should be done in our future work. Finally, the embedded feature selection method will also be studied in the future, because it simultaneously integrates modeling with feature selection and tends to have better coordination between feature selection and model induction.
VII. Conclusion
In this paper, we proposed a disentangled-multimodal adversarial autoencoder to address the ineffective information fusion in multimodal neuroimaging-based infant age prediction. Together with cross-reconstruction and common-specific ratio regulations, a latent variable disentanglement strategy was introduced, by which the correlation among multiple modalities is exploited and the possible noise from the entanglement of the modalities is avoided. Experimental results on infant age prediction with both sMRI and fMRI data validate the superiority of our model over several state-of-the-art methods. Our proposed DMM-AAE serves as a promising model for prediction with multimodal data and a potential means of studying normal and abnormal brain development.
Supplementary Material
Acknowledgments
This work was partially supported by NIH grants (MH116225, MH117943, MH104324, MH109773). This work also utilizes approaches developed by an NIH grant (1U01MH110274) and the efforts of the UNC/UMN Baby Connectome Project Consortium.
References
- [1].Cole JH and Franke K, “Predicting age using neuroimaging: innovative brain ageing biomarkers,” Trends in neurosciences, vol. 40, no. 12, pp. 681–690, 2017. [DOI] [PubMed] [Google Scholar]
- [2].Cole JH, Leech R, Sharp DJ, and Initiative ADN, “Prediction of brain age suggests accelerated atrophy after traumatic brain injury,” Annals of neurology, vol. 77, no. 4, pp. 571–581, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Nenadić I, Dietzek M, Langbein K, Sauer H, and Gaser C, “Brainage score indicates accelerated brain aging in schizophrenia, but not bipolar disorder,” Psychiatry Research: Neuroimaging, vol. 266, pp. 86–89, 2017. [DOI] [PubMed] [Google Scholar]
- [4].Franke K, Gaser C, Manor B, and Novak V, “Advanced brainage in older adults with type 2 diabetes mellitus,” Frontiers in aging neuroscience, vol. 5, p. 90, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Cole JH et al. , “Increased brain-predicted aging in treated hiv disease,” Neurology, vol. 88, no. 14, pp. 1349–1357, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Steffener J, Habeck C, O’Shea D, Razlighi Q, Bherer L, and Stern Y, “Differences between chronological and brain age are related to education and self-reported physical activity,” Neurobiology of aging, vol. 40, pp. 138–144, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Luders E, Cherbuin N, and Gaser C, “Estimating brain age using high-resolution pattern recognition: younger brains in long-term meditation practitioners,” Neuroimage, vol. 134, pp. 508–513, 2016. [DOI] [PubMed] [Google Scholar]
- [8].Ronan L et al. , “Obesity associated with increased brain age from midlife,” Neurobiology of aging, vol. 47, pp. 63–70, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Liem F et al. , “Predicting brain-age from multimodal imaging data captures cognitive impairment,” Neuroimage, vol. 148, pp. 179–188, 2017. [DOI] [PubMed] [Google Scholar]
- [10].Cherubini A et al. , “Importance of multimodal mri in characterizing brain tissue and its potential application for individual age prediction,” IEEE journal of biomedical and health informatics, vol. 20, no. 5, pp. 1232–1239, 2016. [DOI] [PubMed] [Google Scholar]
- [11].Gilmore JH, Knickmeyer RC, and Gao W, “Imaging structural and functional brain development in early childhood,” Nature Reviews Neuroscience, vol. 19, no. 3, p. 123, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Li G et al. , “Mapping region-specific longitudinal cortical surface expansion from birth to 2 years of age,” Cerebral cortex, vol. 23, no. 11, pp. 2724–2733, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Zhang H, Shen D, and Lin W, “Resting-state functional mri studies on infant brains: A decade of gap-filling efforts,” NeuroImage, vol. 185, pp. 664–684, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Wang F et al. , “Developmental topography of cortical thickness during infancy,” Proceedings of the National Academy of Sciences, vol. 116, no. 32, pp. 15 855–15 860, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Valizadeh S, Hänggi J, Mérillat S, and Jäncke L, “Age prediction on the basis of brain anatomical measures,” Human brain mapping, vol. 38, no. 2, pp. 997–1008, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Corps J and Rekik I, “Morphological brain age prediction using multi-view brain networks derived from cortical morphology in healthy and disordered participants,” Scientific reports, vol. 9, no. 1, p. 9676, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Hu D, Wu Z, Lin W, Li G, and Shen D, “Hierarchical rough-to-fine model for infant age prediction based on cortical features,” IEEE journal of biomedical and health informatics, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Liu K, Li Y, Xu N, and Natarajan P, “Learn to combine modalities in multimodal deep learning,” arXiv preprint arXiv:1805.11730, 2018. [Google Scholar]
- [19].Toews M, Wells WM, and Zöllei L, “A feature-based developmental model of the infant brain in structural mri,” in International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer, 2012, pp. 204–211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Baltrušaitis T, Ahuja C, and Morency L-P, “Multimodal machine learning: A survey and taxonomy,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 41, no. 2, pp. 423–443, 2018. [DOI] [PubMed] [Google Scholar]
- [21].Kassani PH, Gossmann A, and Wang Y-P, “Multimodal sparse classifier for adolescent brain age prediction,” arXiv preprint arXiv:1904.01070, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Kim H and Mnih A, “Disentangling by factorising,” in International Conference on Machine Learning, 2018, pp. 2649–2658. [Google Scholar]
- [23].Siddharth N et al. , “Learning disentangled representations with semi-supervised deep generative models,” in Advances in Neural Information Processing Systems, 2017, pp. 5925–5935. [Google Scholar]
- [24].Chen TQ, Li X, Grosse RB, and Duvenaud DK, “Isolating sources of disentanglement in variational autoencoders,” in Advances in Neural Information Processing Systems, 2018, pp. 2610–2620. [Google Scholar]
- [25].Benaim S, Khaitov M, Galanti T, and Wolf L, “Domain intersection and domain difference,” in Proceedings of the IEEE International Conference on Computer Vision, 2019, pp. 3445–3453. [Google Scholar]
- [26].Howell BR et al. , “The unc/umn baby connectome project (bcp): an overview of the study design and protocol development,” NeuroImage, vol. 185, pp. 891–905, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Li G et al. , “Computational neuroanatomy of baby brains: A review,” NeuroImage, vol. 185, pp. 906–925, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Li G, Wang L, Shi F, Gilmore JH, Lin W, and Shen D, “Construction of 4d high-definition cortical surface atlases of infants: Methods and applications,” Medical image analysis, vol. 25, no. 1, pp. 22–36, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Wang L et al. , “Volume-based analysis of 6-month-old infant brain mri for autism biomarker identification and early diagnosis,” in International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer, 2018, pp. 411–419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Glasser MF et al. , “A multi-modal parcellation of human cerebral cortex,” Nature, vol. 536, no. 7615, pp. 171–178, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Wu Z, Wang L, Lin W, Gilmore J, Li G, and Shen D, “Construction of 4d infant cortical surface atlases with sharp folding patterns via spherical patch-based group-wise sparse representation,” Human brain mapping, vol. 40, no. 13, pp. 3860–3880, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Urbanowicz RJ, Meeker M, La Cava W, Olson RS, and Moore JH, “Relief-based feature selection: Introduction and review,” Journal of biomedical informatics, vol. 85, pp. 189–203, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Kawakubo H and Yoshida H, “Rapid feature selection based on random forests for high-dimensional data,” MPS, vol. 2012, no. 3, pp. 1–7, 2012. [Google Scholar]
- [34].Makhzani A, Shlens J, Jaitly N, Goodfellow I, and Frey B, “Adversarial autoencoders,” arXiv preprint arXiv:1511.05644, 2015. [Google Scholar]
- [35].Kingma DP and Welling M, “Auto-encoding variational bayes,” arXiv preprint arXiv:1312.6114, 2013. [Google Scholar]
- [36].Fisher A, Rudin C, and Dominici F, “Model class reliance: Variable importance measures for any machine learning model class, from the rashomon perspective,” arXiv preprint arXiv:1801.01489, 2018. [Google Scholar]
- [37].Armstrong RA, “When to use the bonferroni correction,” Ophthalmic and Physiological Optics, vol. 34, no. 5, pp. 502–508, 2014. [DOI] [PubMed] [Google Scholar]
- [38].Wilson C, Li K, Yu X, Kuan P, and Wang X, “Multiple-kernel learning for genomic data mining and prediction,” BMC bioinformatics, vol. 20, no. 1, pp. 1–7, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Yuan L, Wang Y, Thompson P, Narayan V, and Ye J, “Multi-source learning for joint analysis of incomplete multi-modality neuroimaging data,” in the 18th ACM SIGKDD. ACM, 2012, pp. 1149–1157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Speed T, Statistical analysis of gene expression microarray data. Chapman and Hall/CRC, 2003. [Google Scholar]
- [41].Troyanskaya O et al. , “Missing value estimation methods for dna microarrays,” Bioinformatics, vol. 17, no. 6, pp. 520–525, 2001. [DOI] [PubMed] [Google Scholar]
- [42].Hastie T, Mazumder R, Lee J, and Zadeh R, “Matrix completion and low-rank svd via fast alternating least squares,” The Journal of Machine Learning Research, vol. 16, no. 1, pp. 3367–3402, 2015. [PMC free article] [PubMed] [Google Scholar]
- [43].Maaten L and Hinton G, “Visualizing data using t-sne,” Journal of machine learning research, vol. 9, no. Nov, pp. 2579–2605, 2008. [Google Scholar]
- [44].Menary K et al. , “Associations between cortical thickness and general intelligence in children, adolescents and young adults,” Intelligence, vol. 41, no. 5, pp. 597–606, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Khundrakpam B, Lewis J, Kostopoulos P, Carbonell F, and Evans A, “Cortical thickness abnormalities in autism spectrum disorders through late childhood, adolescence, and adulthood: a large-scale mri study,” Cerebral Cortex, vol. 27, no. 3, pp. 1721–1731, 2017. [DOI] [PubMed] [Google Scholar]
- [46].Li G, Lin W, Gilmore J, and Shen D, “Spatial patterns, longitudinal development, and hemispheric asymmetries of cortical thickness in infants from birth to 2 years of age,” Journal of neuroscience, vol. 35, no. 24, pp. 9150–9162, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Li Y, Pan Q, Wang S, Peng H, Yang T, and Cambria E, “Disentangled variational auto-encoder for semi-supervised learning,” Information Sciences, vol. 482, pp. 73–85, 2019. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


