Abstract
Video-based point cloud compression (V-PCC) is a state-of-the-art moving picture experts group (MPEG) standard for point cloud compression. V-PCC can be used to compress both static and dynamic point clouds in a lossless, near lossless, or lossy way. Many objective quality metrics have been proposed for distorted point clouds. Most of these metrics are full-reference metrics that require both the original point cloud and the distorted one. However, in some real-time applications, the original point cloud is not available, and no-reference or reduced-reference quality metrics are needed. Three main challenges in the design of a reduced-reference quality metric are how to build a set of features that characterize the visual quality of the distorted point cloud, how to select the most effective features from this set, and how to map the selected features to a perceptual quality score. We address the first challenge by proposing a comprehensive set of features consisting of compression, geometry, normal, curvature, and luminance features. To deal with the second challenge, we use the least absolute shrinkage and selection operator (LASSO) method, which is a variable selection method for regression problems. Finally, we map the selected features to the mean opinion score in a nonlinear space. Although we have used only 19 features in our current implementation, our metric is flexible enough to allow any number of features, including future more effective ones. Experimental results on the Waterloo point cloud dataset version 2 (WPC2.0) and the MPEG point cloud compression dataset (M-PCCD) show that our method, namely PCQAML, outperforms state-of-the-art full-reference and reduced-reference quality metrics in terms of Pearson linear correlation coefficient, Spearman rank order correlation coefficient, Kendall’s rank-order correlation coefficient, and root mean squared error.
Keywords: Point cloud compression, perceptual quality metric, feature selection, LASSO regression, support vector regression
I. Introduction
Point clouds enable a realistic representation of three-dimensional (3D) objects [1] [2]. A point cloud consists of a set of points, each of which is characterized by its 3D coordinates, together with attributes such as color, surface normal, and reflectance. As the data size of a point cloud is typically huge, point cloud compression is critical for efficient storage and transmission [3]. The moving picture experts group (MPEG) has been developing two point cloud compression (PCC) standards: geometry-based point cloud compression (G-PCC) [4] and video-based point cloud compression (V-PCC) [5]. In these two standards, quantization of the geometry and attribute information leads to reconstruction errors [6].
In addition to quantization errors, data acquisition and transmission over an unreliable channel may produce further distortions in the geometry and color information. The diversity of factors that cause distortion make point cloud quality assessment a challenging task. Objective quality assessment metrics for a point cloud can be divided into three categories: full-reference (FR), reduced-reference (RR), and no-reference (NR). The main FR quality metrics are the point-to-point [7], point-to-plane [8], point-to-mesh [9], angular similarity [10], graph similarity [11] [12], and curvature [13] metrics. These metrics compute the difference between the reference and distorted point clouds with respect to the geometry, color, normal, curvature, and structural information. However, FR point cloud quality metrics are usually used only at the encoder side because they need the whole original point cloud information, which is not available at the decoder side. Generally, RR point cloud quality metrics extract a small amount of information from the reference and distorted point clouds, and then compare and analyze the extracted feature data to predict the point cloud quality [14] [15]. NR quality metrics do not require any information from the original point cloud and extract and analyze features from the distorted point cloud only. Inspired by NR image quality assessment [16], the existing NR point cloud quality metrics also tend to use deep learning techniques [17] [18] [19]. Since NR and RR point cloud quality assessment metrics can be applied to the whole communication system, their application field is wider than FR metrics. On the other hand, as RR metrics extract more information from the original point cloud than NR metrics, their prediction accuracy is normally higher.
RR point cloud quality metrics can be split into two categories according to the features used. Metrics in the first category focus on distortion caused by compression and rely on compression parameters [14]. Taking into account the sensitivity of the human visual system to structural and chromatic information [20], metrics in the second category use features derived from the luminance, geometry, and normals of the points [15]. Metrics in both categories map the feature space to a quality score via simple linear models. Previous studies have shown that the proposed features can reflect the quality of point clouds to a certain extent. However, in real-time applications, where computing resources are scarce, it is not advisable to use too many features. Determining how to select from a large set of candidate features a small subset of features that simultaneously ensure accuracy of the metric and meet the time complexity requirements of the underlying system is a major challenge. Moreover, exploring whether there is a more effective model than a linear model to map the selected features to a quality score is another key issue. Finally, as more effective features are likely to emerge, building a model that can easily incorporate new features is also an important challenge.
In this paper, we propose an RR quality assessment metric for static point clouds compressed with V-PCC. We focus on V-PCC as it gives state-of-the-art compression results. Drawing upon the sensitivity of the human visual system to structure and color information, we extract several associated features. These include geometry, luminance, normals, and curvature features. At the same time, building upon the fact that quantization can significantly affect the reconstruction quality of the compressed point cloud, we use the V-PCC geometry and color quantization parameters as additional features. In summary, quantization, geometry, luminance, normal, and curvature features form our feature candidate pool (FCP). Then, we use the least absolute shrinkage and selection operator (LASSO) [21] estimator to select a subset of features from the FCP based on their importance for the perceptual quality of the point cloud. Here, we determine the importance of a feature by its absolute coefficient in the LASSO regression. Finally, we fuse the selected features with support vector regression (SVR) [22]. We use SVR because it can handle high-dimensional data and is very robust [23] [24] [25]. Note that the novelty of our model lies not only in the extracted features but also in effectively using these features while considering the practicality of real-world transmission systems and the scalability of the method. Our method is flexible and can be used with any initial set of features. Thus, if more effective features are developed in the future, including them in the feature candidate pool is expected to improve our results. Since our method minimizes the number of selected features according to their predictive importance, its time complexity is markedly lower than that of competing methods that use a larger number of predictors.
The main contributions of this paper are as follows:
We propose an RR point cloud quality metric based on SVR. SVR can learn complex data patterns for an effective and generalizable mapping of the features to a target score. This approach can address the challenge of model parameter estimation for a model that aims at emulating the complex human visual system characteristics.
The proposed RR quality metric is built on a comprehensive candidate feature pool consisting of compression, geometry, normal, curvature and luminance features. While 19 features are used in our current implementation, our metric is flexible enough to accommodate any number of features, including future more effective ones.
The LASSO estimator is adopted to select the most important features. Using this small subset of features reduces the complexity of the model and improves its accuracy.
Experimental results on two benchmark datasets show that for almost all the tested point clouds the proposed method achieves better performance than 14 traditional and state-of-the-art FR and RR methods.
The remainder of this paper is organized as follows. Section II gives an overview of FR, RR, and NR point cloud quality metrics. Section III presents our SVR-based point cloud quality prediction method. Section IV validates the proposed method on the WPC2.0 and M-PCCD datasets. Finally, Section V concludes the paper.
II. Related Work
FR point cloud quality evaluation methods can be divided into four categories: point-based, plane-based, projection-based and feature-based. The most representative point-based point cloud quality metric is the point-to-point peak signal-to-noise ratio (PSNR).The PSNR can be calculated for the geometry information with either the Euclidean distance () [9] or Hausdorff distance () [26] between each point in the reference point cloud and its nearest neighbor in the distorted point cloud. For the color information, the PSNR () [27] is usually calculated using the mean squared error between the luminance of the points in the reference point cloud and the luminance of the nearest points in the distorted point cloud. Another popular metric for the geometry information is the plane-based PSNR [8], which can be computed for the Euclidean or Hausdorff distance ( and , respectively).Alternatively, the projection-based point cloud quality metrics , , , and use the image quality assessment methods [28] [29], [30], [31], [32], and PSNR, respectively, to predict the quality of the point cloud from the average quality of six projection images.
Except that, Yang et al. [33] projected the 3D point cloud onto six perpendicular image planes of a cube for the color texture image and depth image, and aggregate image-based global and local features among all projected planes for the final quality. Feature-based point cloud quality metrics such as PCQM [34] and PointSSIM [35], evaluate the point cloud quality by fitting a set of features. Diniz, Freitas, and Farias [36] proposed a framework to design visual quality metrics for point cloud contents that are based on the statistics of local binary pattern-based texture descriptors and the local color patterns descriptor. Xu et al. [37] quantified the distortion using energy differences by comparing the elastic potential energy differences between reference and distorted point clouds. On this basis, Yang et al. [38] further proposed potential energy discrepancy to quantify point cloud distortion. While Lu et al. [39] exploited edge feature which extracted by the dual-scale 3D-DOG filters. Viola, Subramanyam, and Cesar [40] extracted one color histogram feature and used the histogram distance as a measure of distortion of a test point cloud with respect to a reference. However, a single color histogram feature cannot easily measure various point cloud quality degradations. Unlike the above metrics, GraphSIM [11] constructs a graph in the reference and distorted point clouds to calculate a similarity index.
RR quality metrics usually extract features from the point cloud, analyze the loss of feature information, then predict the quality of the point cloud. Zhou et al. [41] utilize the content-oriented similarity and statistical correlation measurements features from the projected saliency maps of point cloud to evaluate the perceptual quality of point clouds. Viola and Cesar [15] extract 21 geometry, normal, and luminance features from the reference and distorted point clouds and build an RR quality metric () as a weighted sum of their absolute differences. However, compression features are not considered, there is no feature selection, and the model is limited by the linearity constraint. Liu et al. [14] predicted the point cloud quality by applying linear fitting to compression features (). Although the prediction accuracy is high, the method uses only compression features and only linearly weighted features to predict the point cloud quality.
NR quality metrics usually use deep learning techniques to predict the quality of the point cloud. Tao et al. [17] build 2D color and geometry projection maps, and exploit a multi-scale feature fusion network to blindly evaluate the quality of the point cloud. Liu et al. [18] design a feature extraction module to extract features from multiple projections of the point cloud and use the point cloud distortion type classification task to pre-train it. Instead of transforming a 3D point cloud into several 2D projection images, Liu et al. [19] directly use a stack of sparse convolutional layers and residual blocks to extract features in 3D space. Then a global pooling module and a regression module are used to map the feature vectors to a quality score. Tu et al. [42] designed a dual-stream convolutional network from the perspective of global and local feature description to extract texture and geometry features of the projection maps generated from distorted point cloud. While Liu et al. [43] proposed a NR metric ResSCNN based on sparse convolutional neural network to accurately estimate the subjective quality of point clouds. However, the above-mentioned deep learning networks are relatively complex. In addition to metrics based on deep learning, Su et al. [44] proposed one of the first attempts developing a bitstream-based no-reference model by using the encoding parameters for perceptual quality assessment of compressed point clouds.
III. Proposed Quality Metric
Extracting features from a point cloud and mapping them to an accurate measure of perceptual quality is a very challenging problem due to the complex nature of the human visual system. To simplify this problem, we attack it in three steps. In the first step, we build a large pool of potential features. In the second step, we use an optimization process to select the most important features from this pool. Since linear models [14] [15] [34] [35] have been successfully used to map features to a quality score, we use the LASSO linear regression method for feature selection. In the third step, we use a machine learning algorithm to map the selected features to a visual quality score. As a machine learning algorithm, we adopt SVR, which can handle both linear and non-linear regression problems.
Fig. 1 illustrates our framework. The process is composed of three stages: feature extraction to generate the FCP, feature selection, and SVR. In the feature extraction stage, we extract 19 features covering the characteristics of compression, geometry, luminance, normal, and curvature. In the second stage, we use the LASSO estimator to select the most important features. In the third stage, SVR is used to map the selected features to a final point cloud quality score.
Fig. 1.
Proposed RR point cloud quality assessment (PCQAML) framework. MOS denotes mean opinion score.
A. Feature Extraction
The RR metric needs to extract a set of features to predict the level of distortion in the content under assessment. Considering the factors affecting the quality of the compressed point cloud, we extract the following features to form the FCP.
1). Compression Features:
So far, MPEG has standardized two point cloud compression schemes: V-PCC(focusing on immersive communication) and G-PCC(focusing on autonomous driving) [45]. In the V-PCC encoder, the point cloud sequence is converted into a set of 2D images along six projection planes. Then state-of-the-art video codecs are used to compress the geometry and color information separately. During the compression process, the main distortion is generated by quantization which is controlled by a geometry quantization parameter (QP) and a color QP. Therefore, we use the geometry QP () and color QP () as features reflecting compression distortion.
2). Geometry Features:
The geometry features are based on the coordinate information of the points [35].
Consider a distorted point cloud formed of points , , where , , are the geometry coordinates and , , are the intensity values of the red, green, and blue components, respectively. We use the K-nearest neighbor (KNN) search method [46] to determine the set of the nearest neighbors of the point . Then, the variance (), median (), mean absolute deviation (), median absolute deviation (), and coefficient of variation () for every point are obtained as
| (1) |
where is the Euclidean distance between and its -th nearest neighbor in , is the mean value of the Euclidean distances between and its nearest neighbors, and is the median operator. For the point cloud , we build five geometry features , , , , and defined as the mean values of , , , , and , .
3). Normal Features:
The normal features are built to reflect the uniformity of the shape of the local surface. We first obtain the normal of each point in from the coordinate information [35]. Then, we compute the angular similarity between the normal vector of and its nearest neighbors [47]. Next, we compute the variance, median, mean absolute deviation, median absolute deviation, and coefficient of variation of the angular similarity for every point as in (1). Finally, as in 2), we obtain five normal features (, , , , and ) by computing the mean values over all points in the distorted point cloud.
4). Curvature Features:
The curvature can be calculated by the methods in [13] [35] [48]. We use a curvature prediction algorithm from the point cloud library [48] to calculate the curvature of each point . To better consider the structural relationship between the current point and its neighbors, we calculate the standard deviations
| (2) |
where is the set of curvature values of the points in . Then the maximum (), average of maximum and minimum values (), and standard deviation () of are calculated as
| (3) |
For consistency of notation, we call these curvature features , , and , respectively.
5). Luminance Features:
When extracting color features, we work in the luminance channel as it shows a better correlation with the human perception of colors [49]. We convert the color attributes R, G, B at each point into Y, , components using the matrix defined in ITU-R Recommendation BT.709 [50]. Then, for each point in the distorted point cloud, we compute the standard deviation of the luminance of its nearest neighbors. Finally, we take as luminance features , , , and , that is, the maximum, the average of maximum and minimum values, mean, and standard deviation of , .
To evaluate how well the features in the FCP are related to the perceptual quality, the MOSs computed from the ratings of subjects participating in an experiment are used as the ground truth. The correlation between every independent feature and MOS is typically benchmarked with the application of a four-parameter regression model [51]
| (4) |
where is the value of a feature, is the fitted objective score using the feature value, and the parameters are chosen to minimize the least-squares error between the subjective score and the fitted objective score. For an ideal match between the independent features and the subjective quality scores, both the Pearson linear correlation coefficient (PLCC) [52] and the Spearman rank order correlation coefficient (SRCC) [53] should be equal to 1. Fig. 2 shows that all the features are correlated with MOS to some extent. However, considering the time and hardware cost of the quality metric, it is necessary to select as few and as effective features as possible.
Fig. 2.
PLCC (blue bars) and SRCC (green bars) for each feature.
B. Feature Selection
Although the features in FCP have varying degrees of impact on the quality of the point cloud, it is not realistic to use them all, because this would greatly increase the time complexity of the quality metric and may cause over-fitting. Therefore, it is necessary to select the most effective features from FCP.
Feature selection in the context of regression consists of finding the best subset of features to minimize the objective function. The problem can be formulated as an norm regularized minimization problem which, in general, is NP-hard [54] [55]. Under certain mild conditions, the norm can provide the tightest convex approximation to the norm [56]. When the norm is used, LASSO [21] can produce an optimal convex approximation to the best subset selection regression [21]. LASSO estimates a vector of linear regression coefficients by minimizing the residual sum of squares penalized by the norm of the coefficient vector. That is, LASSO solves the optimization problem
| (5) |
where is a non-negative hyper-parameter, is an vector of target MOSs, is a vector of coefficients, is an matrix of features for all the used point clouds, is the number of features, and is the number of training point clouds. The LASSO estimator typically results in many zero coefficients and thus has the ability for variable selection. To determine an appropriate , we use a five-fold cross-validation splitting strategy.
More specifically, theoretical results have been established for LASSO considering the following regression model,
| (6) |
where and are as in Eq. (5), is assumed to be the (unknown) true coefficient vector, and is an -dimensional noise vector. When the set of true regression coefficients is sparse, one assumes that has a sparsity level of . The nonzero coefficients of correspond to informative features, while the others to non-informative ones.
C. Feature Fusion
SVR is a powerful machine learning method frequently used in many applications [57] [58]. In this paper, we formulate the point cloud quality prediction problem as the regression task of mapping the selected features to a quality score.
Let be the number of features selected with LASSO. Given training point clouds and their associated subjective quality scores , we first extract the feature vector of each point cloud . Next, we use -SVM regression [59] to build a function that maps any input feature vector to a quality score . Function is built such that the deviation from to is at most for all , with
| (7) |
where and are nonnegative numbers, is a kernel function, and is a bias. The coefficients and are obtained by minimizing the function
| (8) |
where is a parameter. To solve this optimization problem, we use sequential minimal optimization (SMO) [60].
Any function satisfying Mercer’s requirements can be used as a kernel function [59]. In this paper, we use the three classical kernel functions listed in Table I.
TABLE I.
Kernel Functions.
| Kernel name | Parameters | |
|---|---|---|
|
| ||
| Linear | - | |
| Polynomial | , c, d | |
| Radial basis function (RBF) | ||
IV. Experimental Results
A. Datasets
We assessed the performance of our quality metric on the Waterloo point cloud dataset version 2 (WPC2.0) [14] and on the MPEG point cloud compression dataset (M-PCCD) [61].
The WPC2.0 dataset contains 400 distorted static point clouds obtained by using the MPEG V-PCC test model v7 [62] to compress 16 reference point clouds at 25 distortion levels. These 25 levels were obtained with all combinations of five geometry quantization parameters and five color quantization parameters. The MPEG point cloud dataset (M-PCCD) [61] consists of eight static point clouds. We built 40 distorted point clouds by compressing the point clouds in M-PCCD with the five V-PCC geometry-color QP pairs ((24,33), (24,30), (20,27), (18,20), and (16,16)).
For the WPC2.0 dataset, 30 subjects consisting of 15 males and 15 females aged between 20 and 35 took part in the study. For the M-PCCD dataset, the subjective evaluation experiments took place at EPFL and UNB. Both the EPFL and UNB experiments involved 40 subjects: 16 females and 24 males with an average age of 23.4 at EPFL, and 14 females and 26 males with an average age of 24.3 at UNB. More details can be found in [14] and [61].
B. Methodology Implementation
Many LASSO models were built with iterative fitting along a regularization path, and the best model was selected by fivefold cross-validation. All the training parameters followed the default values in Scikit-learn [63]. Features whose importance were greater than or equal to the threshold 10−5 were kept while the others were discarded.
The selected features and the corresponding MOSs were used as input to the SVR regression module to train the point cloud quality model with the LIBSVM package [64]. When deploying SVR to train the prediction module, the parameters , were used. In Table I, the parameters and of the polynomial kernel were set to 0.01 and 4, respectively, and the parameter of the polynomial and RBF kernels was set to the value that provided the highest PLCC. We chose the LIBSVM package [64] for regression because of its convenience for parameter selection [65].
C. Quality Assessment Results
1). Feature Selection:
Fig. 3 shows the importance of the 19 features for MOS on the WPC2.0 dataset. We can see that the four features, , , , and were more important than the remaining 15 features, and that their importance exceeded the threshold 10−5. Therefore, we only retained these four features as input features to the SVR regression module. It is worth noting that the feature importance of and is significantly better than that of other features. This result can be explained as follows. PCQAML is designed for point clouds compressed with V-PCC. V-PCC converts the input point cloud sequence into two video sequences and encodes each video with H.265. The point cloud sequence is then reconstructed from the decoded videos. As the reconstruction accuracy of the two videos decreases with increasing quantization error, the two quantization parameters and play the most important role in the point cloud distortion.
Fig. 3.
Importance of the 19 features with respect to MOS using the LASSO estimator on the WPC2.0 dataset. The vertical axis represents the absolute value of the logarithm of the feature value.
2). Accuracy of the Proposed PCQAML:
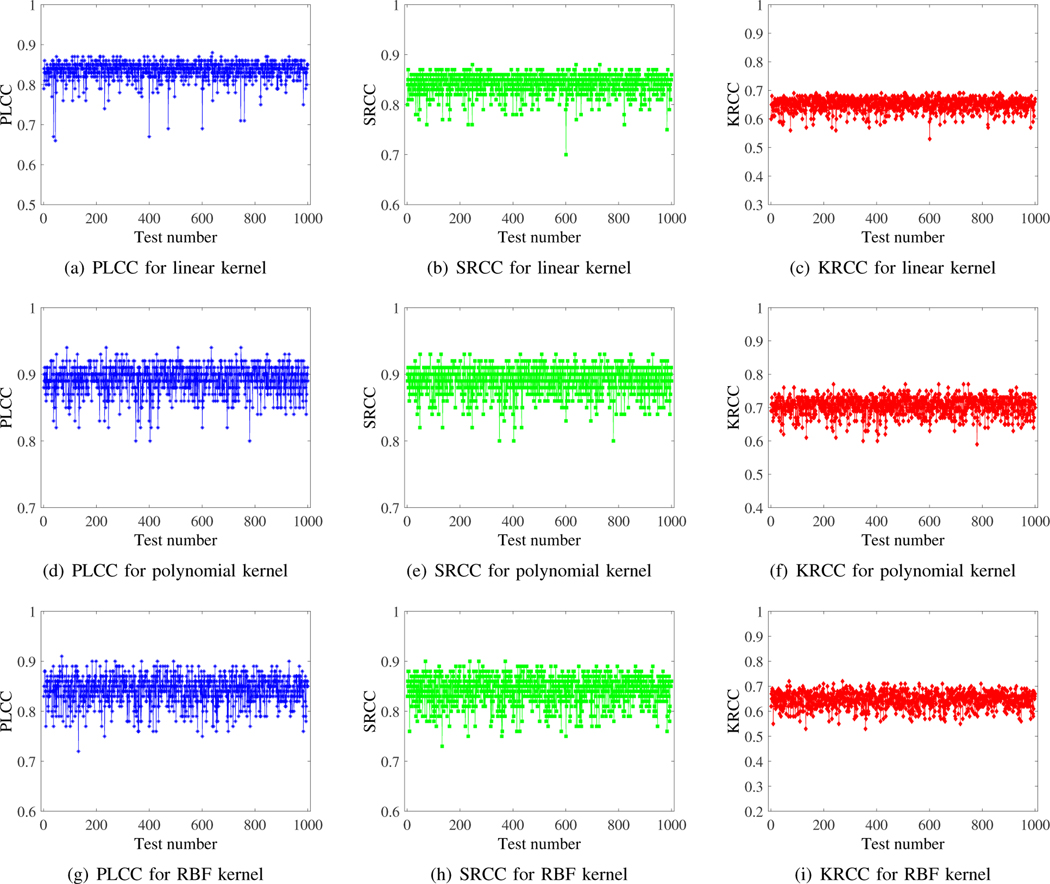
The common evaluation criteria PLCC, SRCC, Kendall’s rank-order correlation coefficient (KRCC) [66], mean absolute error (MAE), and root mean squared error (RMSE) were adopted to compare the accuracy of the objective evaluation methods. PLCC represents the linear correlation between the predicted objective scores and the subjective scores. SRCC can evaluate the prediction monotonicity. MAE represents the average value of the difference between the predicted objective scores and the subjective scores. RMSE is a measure of deviation between the predicted scores and the subjective scores. In general, for an accurate visual quality assessment method the PLCC and SRCC should be close to 1, and the MAE and RMSE should be close to 0. To evaluate the accuracy and reliability of the proposed PCQAML with different kernel functions, we calculated the PLCC, SRCC, KRCC, MAE, and RMSE between the ground truth MOS and predicted MOS 1000 times. Each time, 50% of the distorted point clouds are randomly selected from the dataset, while the remaining 50% point clouds in the dataset are treated as the testing set. There is no overlap between the training set and the testing set. Fig. 4 shows the results for the WPC2.0 dataset. The results confirm the accuracy of the proposed model with different kernel functions. Although there is not a huge difference between the performance of the different kernels, the polynomial and RBF kernels were relatively more effective. This is because they can handle non-linear problems, while the linear kernel can handle only linear ones.
Fig. 4.
PLCC, SRCC, and KRCC of the proposed PCQAML with different kernel functions for WPC2.0. The calculations are repeated 1000 times, each time with a randomly selected subset of point clouds.
To further compare the performance of different kernels and verify the reliability of the proposed PCQAML, we computed various statistics such as the mean, median, maximum, minimum, mode, and variance, of 1000 repeated experimental results. The results in Table II show that the proposed PCQAML was stable for all kernels as the variance was low. The results also show that the polynomial and RBF kernels gave high-quality results with the best performance achieved with the polynomial kernel followed by the RBF kernel. Since the RBF kernel requires fewer hyper-parameters than the polynomial kernel, we adopted it along with the polynomial kernel although its performance was lower.
TABLE II.
Statistical results for different kernel functions on WPC2.0
| Kernel | Mean | Median | Maximum | Minimum | Mode | Variance | |
|---|---|---|---|---|---|---|---|
| PLCC | Linear | 0.84 | 0.84 | 0.88 | 0.66 | 0.85 | 0.00 |
| Polynomial | 0.89 | 0.90 | 0.94 | 0.80 | 0.90 | 0.00 | |
| RBF | 0.84 | 0.85 | 0.91 | 0.72 | 0.85 | 0.00 | |
|
| |||||||
| SRCC | Linear | 0.84 | 0.85 | 0.88 | 0.70 | 0.85 | 0.00 |
| Polynomial | 0.89 | 0.89 | 0.93 | 0.80 | 0.90 | 0.00 | |
| RBF | 0.84 | 0.85 | 0.90 | 0.73 | 0.86 | 0.00 | |
|
| |||||||
| KRCC | Linear | 0.65 | 0.65 | 0.69 | 0.53 | 0.66 | 0.00 |
| Polynomial | 0.70 | 0.71 | 0.77 | 0.59 | 0.72 | 0.00 | |
| RBF | 0.65 | 0.65 | 0.72 | 0.53 | 0.66 | 0.00 | |
|
| |||||||
| MAE | Linear | 9.44 | 9.335 | 13.33 | 8.25 | 9.18 | 0.36 |
| Polynomial | 7.75 | 7.65 | 10.56 | 5.70 | 7.49 | 0.50 | |
| RBF | 9.24 | 9.155 | 11.99 | 7.57 | 8.67 | 0.55 | |
|
| |||||||
| RMSE | Linear | 12.05 | 11.91 | 16.46 | 10.68 | 11.77 | 0.53 |
| Polynomial | 9.89 | 9.78 | 13.14 | 7.36 | 9.47 | 0.77 | |
| RBF | 11.78 | 11.715 | 15.33 | 9.52 | 12.37 | 0.92 | |
We also repeated the experiment 1000 times with different kernel functions to verify the reliability of the proposed quality model on M-PCCD. The average PLCC, SRCC, and KRCC are shown in Table III. We can see that the average PLCC of the proposed quality model with different kernel functions was larger than 0.82, confirming its effectiveness on a different dataset. Note how the PLCC was similar on the two datasets, indicating the reliability of the proposed quality model.
TABLE III.
Mean results of the proposed PCQAML using different kernel functions on M-PCCD
| Kernel | PLCC | SRCC | KRCC | MAE | RMSE |
|---|---|---|---|---|---|
|
| |||||
| Linear | 0.82 | 0.80 | 0.62 | 0.48 | 0.58 |
| Polynomial | 0.86 | 0.80 | 0.62 | 0.43 | 0.51 |
| RBF | 0.83 | 0.78 | 0.60 | 0.47 | 0.57 |
3). Results without Feature Selection:
To illustrate the effectiveness of the feature selection module, we give the results with feature selection (PCQAML) and without(PCQAML_W/O_FS). The RBF kernel was used in this experiment. For a fair comparison, the same training and test sets were used. The results are presented in Table IV. They show that in all cases PCQAML gave the same or better results than PCQAML W/O FS. We explain this as follows. PCQAML_W/O_FS performed less effectively than PCQAML due to its use of a large number of features, leading to overfitting. Note that PCQAML significantly reduced the time complexity as it uses four features instead of 19.
TABLE IV.
Comparison between PCQAML_W/O_FS and PCQAML with RBF kernel on WPC2.0. (s) indicates that PCQAML gave the same results as PCQAML_W/O_FS, (b) indicates that it gave better results.
| Method Name | Metric | Mean | Median | Maximum | Minimum | Mode | Variance |
|---|---|---|---|---|---|---|---|
|
| |||||||
| PCQAML_W/O_FS | PLCC | 0.84 | 0.84 | 0.91 | 0.69 | 0.84 | 0.00 |
| SRCC | 0.83 | 0.84 | 0.90 | 0.70 | 0.84 | 0.00 | |
| KRCC | 0.64 | 0.64 | 0.72 | 0.50 | 0.64 | 0.00 | |
|
| |||||||
| PCQAML | PLCC | 0.84(S) | 0.85(B) | 0.91(S) | 0.72(B) | 0.85(B) | 0.00(B) |
| SRCC | 0.84(B) | 0.85(B) | 0.90(S) | 0.73(B) | 0.86(B) | 0.00(S) | |
| KRCC | 0.65(B) | 0.65(B) | 0.72(S) | 0.53(B) | 0.66(B) | 0.00(S) | |
some of the comparison results of these two methods are the same. In some cases, the results show that PCQAML is slightly more accurate than PCQAML_W/O_FS. The main reason is that PCQAML_W/O_FS used 19 features, which led to overfitting; that is, the prediction of the machine learning model on the training set is much more accurate than on the test set. More importantly, PCQAML significantly reduces the time complexity as it uses four features instead of 19.
4). Comparison with FR and RR Methods:
In this section, we compare our method with 14 traditional and state-of-the-art FR and RR point cloud quality metrics on WPC2.0 (Table V). In our method, we used the polynomial kernel. In GraphSIM, we used the same parameters as in [11]. The FR metrics were chosen to cover diverse design strategies, including point-based, plane-based, projection-based and feature-based ones. As RR point cloud quality metric benchmarks, we used [14] and [15].
TABLE V.
Comparison with FR and RR point cloud quality metrics on WPC2.0
| Type | Method | Metric | bag | cake | cauliflower | mushroom | ping-pong_bat | puer_tea | ship | statue | Overall |
|---|---|---|---|---|---|---|---|---|---|---|---|
| FR | [9] | 0.77 | 0.86 | 0.79 | 0.56 | 0.70 | 0.38 | 0.96 | 0.86 | 0.46 | |
| 0.69 | 0.78 | 0.76 | 0.51 | 0.68 | 0.40 | 0.91 | 0.87 | 0.28 | |||
| 0.55 | 0.65 | 0.63 | 0.42 | 0.55 | 0.31 | 0.79 | 0.74 | 0.20 | |||
| MAE | 10.56 | 8.09 | 11.00 | 15.03 | 13.98 | 18.18 | 4.83 | 8.46 | 16.80 | ||
| RMSE | 13.23 | 9.91 | 13.52 | 17.04 | 17.34 | 21.28 | 5.98 | 11.18 | 19.55 | ||
|
| |||||||||||
| [8] | 0.77 | 0.86 | 0.79 | 0.56 | 0.70 | 0.38 | 0.96 | 0.86 | 0.48 | ||
| 0.69 | 0.78 | 0.76 | 0.51 | 0.68 | 0.40 | 0.91 | 0.87 | 0.33 | |||
| 0.55 | 0.65 | 0.63 | 0.42 | 0.55 | 0.31 | 0.79 | 0.74 | 0.24 | |||
| MAE | 10.56 | 8.09 | 11.00 | 15.03 | 13.98 | 18.18 | 4.84 | 8.46 | 16.43 | ||
| RMSE | 13.23 | 9.90 | 13.52 | 17.03 | 17.34 | 21.29 | 5.98 | 11.18 | 19.30 | ||
|
| |||||||||||
| [9] | 0.77 | 0.86 | 0.79 | 0.54 | 0.70 | 0.35 | 0.93 | 0.36 | 0.33 | ||
| 0.69 | 0.78 | 0.76 | 0.47 | 0.68 | 0.35 | 0.83 | 0.38 | 0.22 | |||
| 0.56 | 0.65 | 0.62 | 0.37 | 0.55 | 0.26 | 0.69 | 0.26 | 0.15 | |||
| MAE | 10.56 | 8.10 | 11.00 | 18.70 | 13.98 | 19.79 | 6.07 | 19.36 | 18.23 | ||
| RMSE | 13.23 | 9.94 | 13.50 | 20.52 | 17.34 | 22.96 | 7.46 | 21.94 | 20.74 | ||
|
| |||||||||||
| [8] | 0.77 | 0.86 | 0.79 | 0.52 | 0.70 | 0.37 | 0.95 | 0.67 | 0.34 | ||
| 0.69 | 0.78 | 0.76 | 0.46 | 0.68 | 0.40 | 0.91 | 0.54 | 0.29 | |||
| 0.56 | 0.65 | 0.62 | 0.36 | 0.55 | 0.32 | 0.79 | 0.42 | 0.21 | |||
| MAE | 10.56 | 8.11 | 11.00 | 15.25 | 13.98 | 18.18 | 4.84 | 13.70 | 18.12 | ||
| RMSE | 13.23 | 9.90 | 13.50 | 17.51 | 17.34 | 21.29 | 6.03 | 16.34 | 20.69 | ||
|
| |||||||||||
| [26] | 0.86 | 0.64 | 0.66 | 0.89 | 0.84 | 0.95 | 0.61 | 0.67 | 0.43 | ||
| 0.84 | 0.69 | 0.66 | 0.89 | 0.80 | 0.93 | 0.64 | 0.67 | 0.41 | |||
| 0.67 | 0.55 | 0.54 | 0.71 | 0.67 | 0.80 | 0.47 | 0.50 | 0.30 | |||
| MAE | 8.39 | 11.97 | 14.06 | 6.89 | 10.81 | 5.46 | 13.84 | 14.24 | 16.98 | ||
| RMSE | 10.53 | 15.04 | 16.45 | 9.18 | 13.14 | 7.14 | 16.03 | 16.22 | 19.84 | ||
|
| |||||||||||
| 0.78 | 0.88 | 0.84 | 0.58 | 0.81 | 0.69 | 0.97 | 0.92 | 0.22 | |||
| 0.76 | 0.84 | 0.86 | 0.59 | 0.84 | 0.72 | 0.94 | 0.93 | 0.14 | |||
| 0.54 | 0.68 | 0.71 | 0.44 | 0.69 | 0.54 | 0.81 | 0.75 | 0.11 | |||
| MAE | 10.42 | 7.50 | 9.61 | 14.68 | 11.00 | 13.35 | 3.97 | 6.88 | 18.91 | ||
| RMSE | 13.00 | 9.25 | 11.98 | 16.67 | 14.28 | 16.53 | 5.15 | 8.57 | 21.45 | ||
|
| |||||||||||
| [28] | 0.98 | 0.98 | 0.99 | 0.97 | 0.98 | 0.93 | 0.99 | 0.98 | 0.43 | ||
| 0.96 | 0.98 | 0.99 | 0.97 | 0.97 | 0.94 | 0.98 | 0.98 | 0.33 | |||
| 0.85 | 0.91 | 0.92 | 0.87 | 0.89 | 0.79 | 0.90 | 0.88 | 0.24 | |||
| MAE | 3.34 | 3.08 | 2.69 | 3.94 | 3.83 | 6.20 | 2.45 | 3.48 | 17.09 | ||
| RMSE | 4.27 | 4.15 | 3.72 | 5.10 | 4.88 | 8.21 | 2.89 | 4.26 | 19.82 | ||
|
| |||||||||||
| [30] | 0.97 | 0.98 | 0.98 | 0.93 | 0.98 | 0.93 | 0.99 | 0.98 | 0.54 | ||
| 0.96 | 0.98 | 0.99 | 0.92 | 0.97 | 0.93 | 0.98 | 0.98 | 0.50 | |||
| 0.85 | 0.90 | 0.92 | 0.77 | 0.89 | 0.78 | 0.91 | 0.91 | 0.38 | |||
| MAE | 3.88 | 3.12 | 2.85 | 5.97 | 3.63 | 6.75 | 2.33 | 3.54 | 14.98 | ||
| RMSE | 5.08 | 4.19 | 4.04 | 7.79 | 4.69 | 8.58 | 2.91 | 4.34 | 18.44 | ||
|
| |||||||||||
| [32] | 0.97 | 0.96 | 0.97 | 0.96 | 0.97 | 0.98 | 0.97 | 0.98 | 0.80 | ||
| 0.96 | 0.97 | 0.97 | 0.95 | 0.96 | 0.97 | 0.97 | 0.98 | 0.79 | |||
| 0.85 | 0.89 | 0.88 | 0.83 | 0.84 | 0.87 | 0.87 | 0.89 | 0.58 | |||
| MAE | 3.55 | 3.79 | 3.84 | 4.53 | 4.82 | 3.26 | 3.93 | 3.65 | 10.80 | ||
| RMSE | 4.63 | 5.46 | 4.94 | 5.95 | 5.75 | 4.12 | 5.12 | 4.47 | 13.33 | ||
|
| |||||||||||
| PointSSIM [35] | 0.64 | 0.40 | 0.62 | 0.81 | 0.68 | 0.91 | 0.30 | 0.53 | 0.51 | ||
| 0.63 | 0.46 | 0.65 | 0.84 | 0.70 | 0.88 | 0.43 | 0.53 | 0.48 | |||
| 0.49 | 0.33 | 0.49 | 0.68 | 0.58 | 0.75 | 0.29 | 0.41 | 0.34 | |||
| MAE | 12.62 | 14.79 | 14.67 | 9.18 | 14.51 | 7.13 | 17.49 | 16.66 | 16.07 | ||
| RMSE | 15.77 | 17.86 | 17.28 | 12.10 | 17.79 | 9.35 | 19.25 | 18.63 | 18.97 | ||
|
| |||||||||||
| PCQM [34] | 0.84 | 0.63 | 0.67 | 0.84 | 0.78 | 0.91 | 0.40 | 0.53 | 0.62 | ||
| 0.84 | 0.70 | 0.66 | 0.83 | 0.77 | 0.90 | 0.57 | 0.55 | 0.64 | |||
| 0.67 | 0.55 | 0.51 | 0.66 | 0.64 | 0.77 | 0.43 | 0.41 | 0.47 | |||
| MAE | 18.30 | 16.68 | 19.39 | 18.70 | 21.25 | 19.79 | 18.12 | 19.36 | 19.51 | ||
| RMSE | 20.60 | 19.47 | 22.01 | 20.52 | 24.27 | 22.96 | 20.18 | 21.94 | 22.00 | ||
|
| |||||||||||
| GraphSIM [11] | 0.84 | 0.85 | 0.87 | 0.92 | 0.81 | 0.95 | 0.52 | 0.74 | 0.71 | ||
| 0.82 | 0.87 | 0.86 | 0.91 | 0.78 | 0.94 | 0.58 | 0.72 | 0.72 | |||
| 0.63 | 0.70 | 0.67 | 0.77 | 0.63 | 0.80 | 0.41 | 0.53 | 0.52 | |||
| MAE | 8.72 | 7.55 | 8.70 | 6.01 | 11.80 | 5.73 | 14.69 | 12.68 | 12.35 | ||
| RMSE | 11.08 | 10.34 | 10.82 | 7.99 | 14.17 | 7.04 | 17.22 | 14.79 | 15.49 | ||
|
| |||||||||||
| RR | [14] | 0.87 | 0.97 | 0.98 | 0.98 | 0.98 | 0.95 | 0.90 | 0.94 | 0.90 | |
| 0.86 | 0.98 | 0.98 | 0.98 | 0.97 | 0.95 | 0.93 | 0.95 | 0.90 | |||
| 0.67 | 0.89 | 0.91 | 0.89 | 0.87 | 0.82 | 0.77 | 0.81 | 0.73 | |||
| MAE | 8.29 | 3.33 | 3.06 | 3.18 | 4.27 | 5.67 | 7.36 | 6.18 | 7.01 | ||
| RMSE | 10.25 | 5.09 | 3.90 | 4.28 | 5.11 | 7.47 | 8.96 | 7.61 | 8.98 | ||
|
| |||||||||||
| [15] | 0.88 | 0.65 | 0.86 | 0.88 | 0.75 | 0.52 | 0.95 | 0.30 | 0.43 | ||
| 0.88 | 0.61 | 0.94 | 0.88 | 0.91 | 0.57 | 0.93 | 0.29 | 0.43 | |||
| 0.71 | 0.44 | 0.83 | 0.72 | 0.76 | 0.45 | 0.79 | 0.19 | 0.30 | |||
| MAE | 18.30 | 16.68 | 19.39 | 18.70 | 21.25 | 19.79 | 18.12 | 19.36 | 19.51 | ||
| RMSE | 20.60 | 19.47 | 22.01 | 20.52 | 24.27 | 22.96 | 20.18 | 21.94 | 22.00 | ||
|
| |||||||||||
| PCQAML(polynomial) | 0.96 | 0.93 | 0.96 | 0.97 | 0.97 | 0.96 | 0.83 | 0.90 | 0.91 | ||
| 0.92 | 0.94 | 0.94 | 0.96 | 0.94 | 0.96 | 0.85 | 0.86 | 0.91 | |||
| 0.77 | 0.81 | 0.79 | 0.86 | 0.83 | 0.83 | 0.68 | 0.69 | 0.74 | |||
| MAE | 4.69 | 5.63 | 5.08 | 3.68 | 4.56 | 4.61 | 9.28 | 8.37 | 6.84 | ||
| RMSE | 6.08 | 7.36 | 6.42 | 4.80 | 5.67 | 6.20 | 11.16 | 9.73 | 8.98 | ||
We chose the eight point clouds (“bag”, “cake”, “cauliflower”, “mushroom”, “ping − pong_bat”, “puer_tea”, “ship”, and “statue”) for testing and the remaining eight for training. The SRCC, PLCC, KRCC, MAE, and RMSE results are given in Table V. Since the quality ratings predicted by different point cloud quality metrics may have different ranges, we used a four-parameter mapping function [51] to map them to a common space. Note that the quality metrics can either directly evaluate the quality or indirectly predict the quality by evaluating the distortion. Therefore, the criteria (e.g., PLCC, SRCC, and KRCC) can be positive or negative.
As shown in Table V, the methods that only consider the geometry structure or color(i.e., , , , , , and ) did not perform well. The major reason is that point clouds contain both geometric and color information, and it is insufficient to consider only one of them. The performance of the projection-based and feature-based methods that comprehensively consider geometry and color information was significantly better, especially whose PLCC was 0.80 and SRCC was 0.79. Note that the PLCC and SRCC of were only 0.43 with the optimal feature weights provided in [67]. We can explain the poor performance of by the fact that it uses a very large number of features, which limits its generalization ability. In the proposed PCQAML, we overcome this shortcoming by selecting effective features. In addition, does not use compression features, which play an important role in the reconstruction quality of the point cloud. On the other hand, uses the compression features to predict the point cloud quality, resulting in a PLCC rise to 0.90. In contrast, the proposed method considers multiple features, such as compression features, geometry features, normal features, curvature features and luminance features, and selects the most effective ones. As a result, both the PLCC and SRCC of the proposed PCQAML reached 0.91, outperforming the existing point cloud quality methods.
To further verify the performance of the proposed PCQAML, we tested it on M-PCCD. We trained our model on the four points clouds amphoriskos, biplane, loot, and the20smaria, and tested it on the four point clouds head, longdress, romanoillamp and soldier. We used the polynomial kernel in SVR. Table VI shows the PLCC, SRCC, KRCC, MAE, and RMSE. In addition to our method, we provide results for all other methods using their published models. We can see that the proposed metric showed an excellent performance and was more accurate than the state-of-the-art ones.
TABLE VI.
Comparison with FR and RR point cloud quality metrics on M-PCCD
| Type | Method | Metric | head | longdress | romanoillamp | soldier | Overall |
|---|---|---|---|---|---|---|---|
| FR | = [26] | 1.00 | 1.00 | 0.99 | 0.95 | 0.61 | |
| 1.00 | 0.90 | 1.00 | 0.90 | 0.54 | |||
| 1.00 | 0.80 | 1.00 | 0.80 | 0.37 | |||
| MAE | 0.05 | 0.07 | 0.09 | 0.29 | 0.71 | ||
| RMSE | 0.06 | 0.09 | 0.11 | 0.31 | 0.90 | ||
|
| |||||||
| PointSSIM [35] | 1.00 | 1.00 | 0.99 | 0.95 | 0.94 | ||
| 1.00 | 0.90 | 1.00 | 0.90 | 0.91 | |||
| 1.00 | 0.80 | 1.00 | 0.80 | 0.72 | |||
| MAE | 0.04 | 0.08 | 0.11 | 0.26 | 0.34 | ||
| RMSE | 0.05 | 0.10 | 0.13 | 0.30 | 0.39 | ||
|
| |||||||
| PCQM [34] | 0.94 | 0.94 | 0.98 | 0.93 | 0.65 | ||
| 1.00 | 0.90 | 1.00 | 0.90 | 0.68 | |||
| 1.00 | 0.80 | 1.00 | 0.80 | 0.47 | |||
| MAE | 1.06 | 1.06 | 0.98 | 0.90 | 1.00 | ||
| RMSE | 1.22 | 1.13 | 1.10 | 1.00 | 1.13 | ||
|
| |||||||
| GraphSIM [11] | 1.00 | 0.99 | 0.99 | 0.95 | 0.92 | ||
| 1.00 | 0.90 | 1.00 | 0.90 | 0.88 | |||
| 1.00 | 0.80 | 1.00 | 0.80 | 0.71 | |||
| MAE | 0.05 | 0.12 | 0.13 | 0.29 | 0.38 | ||
| RMSE | 0.06 | 0.13 | 0.14 | 0.32 | 0.44 | ||
|
| |||||||
| RR | [14] | 0.99 | 1.00 | 1.00 | 0.96 | 0.61 | |
| 1.00 | 0.90 | 1.00 | 0.90 | 0.61 | |||
| 1.00 | 0.80 | 1.00 | 0.80 | 0.43 | |||
| MAE | 0.11 | 0.06 | 0.07 | 0.27 | 0.76 | ||
| RMSE | 0.12 | 0.08 | 0.07 | 0.29 | 0.89 | ||
|
| |||||||
| [15] | 1.00 | 1.00 | 0.99 | 0.90 | 0.85 | ||
| 1.00 | 1.00 | 1.00 | 0.90 | 0.86 | |||
| 1.00 | 1.00 | 1.00 | 0.80 | 0.67 | |||
| MAE | 1.06 | 1.06 | 0.98 | 0.90 | 1.00 | ||
| RMSE | 1.22 | 1.13 | 1.10 | 1.00 | 1.13 | ||
|
| |||||||
| PCQAML(polynomial) | 0.98 | 1.00 | 1.00 | 0.97 | 0.97 | ||
| 1.00 | 0.90 | 1.00 | 0.90 | 0.93 | |||
| 1.00 | 0.80 | 1.00 | 0.80 | 0.81 | |||
| MAE | 0.23 | 0.04 | 0.04 | 0.25 | 0.24 | ||
| RMSE | 0.26 | 0.06 | 0.05 | 0.26 | 0.27 | ||
In general, the performance of was much higher on WPC2.0 than on M-PCCD, while the converse was true for . This is because the transformation base of the model parameters of was obtained by training on WPC2.0, and the model parameters of were obtained by training on M-PCCD. In both cases, the parameters were determined from the entire sample of the training dataset, which inevitably introduces different degrees of overfitting due to the different sizes of the datasets. In contrast, the parameters of the proposed quality metric are determined from the support vector under relaxed conditions, which overcomes the overfitting problem to a certain extent. This explains why our method was more robust than these two previous methods, achieving a PLCC of more than 0.91 on both datasets.
5). Cross-dataset Validation:
To further verify the robustness of our method, we trained our model on the WPC2.0 dataset with different kernel functions and tested it on the M-PCCD dataset. The results in Table VII show that the proposed approach was still able to deliver competitive performance in a cross dataset setting. The experimental results in this section show that the proposed PCQAML has a strong generalization capability.
TABLE VII.
Cross dataset validation of the proposed PCQAML, trained on WPC2.0 and tested on M-PCCD
| Kernel | PLCC | SRCC | KRCC | MAE | RMSE |
|---|---|---|---|---|---|
| Linear | 0.89 | 0.89 | 0.71 | 0.40 | 0.47 |
| Polynomial | 0.86 | 0.88 | 0.71 | 0.43 | 0.53 |
| RBF | 0.76 | 0.75 | 0.57 | 0.54 | 0.67 |
6). Time Complexity:
An effective point cloud quality assessment metric should both provide an accurate point cloud quality prediction and be computationally efficient. In this subsection, we compare the time complexity of the proposed PCQAML to that of state-of-the-art RR point cloud quality metrics. All competing methods were evaluated in terms of their execution time for eight representative point cloudswith different content complexity levels. Experimental results are shown in Table VIII. The source codes were written in MATLAB R2018a and run on a Windows 7 Pro 64-bit desktop computer with a 8G RAM and 2.8 GHz CPU processor. The metrics. All competing methods were evaluated in terms of proposed PCQAML was not only much faster than , their execution time for eight representative point clouds it also has a relatively low time complexity.
TABLE VIII.
CPU times of RR point cloud quality metrics.
| Point Cloud╲RR quality metrics | PCQAML | ||
|---|---|---|---|
| bag | 11.44 | 482.61 | 27.06 |
|
| |||
| cake | 24.36 | 881.65 | 112.06 |
|
| |||
| cauliflower | 18.75 | 676.61 | 42.65 |
|
| |||
| mushroom | 10.04 | 421.24 | 22.82 |
|
| |||
| ping — pong_bat | 6.69 | 244.21 | 12.15 |
|
| |||
| puer_tea | 3.54 | 165.96 | 8.26 |
|
| |||
| ship | 6.43 | 242.03 | 12.15 |
|
| |||
| statue | 14.78 | 557.04 | 28.53 |
V. Conclusion
We proposed an RR visual quality metric for V-PCC compressed static point clouds. Starting from a large set of features, we used LASSO for optimal feature selection. Then, we applied SVR to map the selected features to a visual quality score. Extensive experimental results on two benchmark datasets showed that our method outperforms state-of-the-art RR and some FR point cloud quality metrics in terms of prediction of the MOS. Future work will include extending our method to V-PCC compressed dynamic point clouds and to G-PCC compressed point clouds, as well as exploring more effective features.
Acknowledgments
This work was supported in part by the National Science Foundation of China under Grant (62222110, 62172259, and 62311530104), in part by the High-end Foreign Experts Recruitment Plan of Chinese Ministry of Science and Technology under Grant G2023150003L, in part by the Taishan Scholar Project of Shandong Province (tsqn202103001), and the Shandong Provincial Natural Science Foundation, China, under Grants (ZR2022MF275, ZR2022QF076, ZR2022ZD038, ZR2021MF025, ZR2022ZD38).
Contributor Information
Honglei Su, College of Electronics and Information, Qingdao University, Qingdao 266071, China..
Qi Liu, College of Electronics and Information, Qingdao University, Qingdao 266237, China..
Hui Yuan, School of Control Science and Engineering, Shandong University, Ji’nan 250061, China..
Qiang Cheng, Department of Computer Science, University of Kentucky, USA..
Raouf Hamzaoui, School of Engineering and Sustainable Development, De Montfort University, Leicester, UK.
References
- [1].Liu Q, Su H, Chen T, Yuan H, and Hamzaoui R, “No-reference bitstream-layer model for perceptual quality assessment of v-pcc encoded point clouds,” IEEE Transactions on Multimedia, vol. 25, pp.4533–4546, 2023. [Google Scholar]
- [2].Liu H, Yuan H, Liu Q, Hou J, and Liu J, “A comprehensive study and comparison of core technologies for MPEG 3-D point cloud compression,” IEEE Transactions on Broadcasting, vol. 66, no. 3, pp. 701–717, 2019. [Google Scholar]
- [3].Javaheri A, Brites C, Pereira F, and Ascenso J, “Point cloud rendering after coding: Impacts on subjective and objective quality,” IEEE Transactions on Multimedia, vol. 23, pp. 4049–4064, 2020. [Google Scholar]
- [4].3DG, “Text of ISO/IEC CD 23090–9: Geometry-based point cloud compression,” ISO/IEC JTC1/SC29/WG11 MPEG N18478, Mar. 2019. [Google Scholar]
- [5].3DG, “Text of ISO/IEC CD 23090–5: Video-based point cloud compression,” ISO/IEC JTC1/SC29/WG11 MPEG N18030, Oct. 2018. [Google Scholar]
- [6].Liu Q, Yuan H, Hou J, Hamzaoui R, and Su H, “Model-based joint bit allocation between geometry and color for video-based 3D point cloud compression,” IEEE Transactions on Multimedia, vol. 23, pp. 3278–3291, 2020. [Google Scholar]
- [7].Girardeau-Montaut D, Roux M, Marc R, and Thibault G, “Change detection on points cloud data acquired with a ground laser scanner,” International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, vol. 36, p. W19, 2005. [Google Scholar]
- [8].Tian D, Ochimizu H, Feng C, Cohen R, and Vetro A, “Geometric distortion metrics for point cloud compression,” in 2017 IEEE International Conference on Image Processing (ICIP), 2017, pp. 3460–3464. [Google Scholar]
- [9].Mekuria R, Li Z, Tulvan C, and Chou P, “Evaluation criteria for PCC (point cloud compression),” ISO/IEC JTC1/SC29/WG11 MPEG N16332, 2016. [Google Scholar]
- [10].Alexiou E. and Ebrahimi T, “Point cloud quality assessment metric based on angular similarity,” in 2018 IEEE International Conference on Multimedia and Expo (ICME), 2018, pp. 1–6. [Google Scholar]
- [11].Yang Q, Ma Z, Xu Y, Li Z, and Sun J, “Inferring point cloud quality via graph similarity,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 44, no. 6, pp. 3015–3029, 2020. [DOI] [PubMed] [Google Scholar]
- [12].Zhang Y, Yang Q, and Xu Y, “MS-GraphSIM: Inferring point cloud quality via multiscale graph similarity,” in Proceedings of the 29th ACM International Conference on Multimedia, 2021, pp. 1230–1238. [Google Scholar]
- [13].Meynet G, Digne J, and Lavoue G, “PC-MSDM: A quality metric for 3D point clouds,” in 2019 Eleventh International Conference on Quality of Multimedia Experience (QoMEX), 2019, pp. 1–3. [Google Scholar]
- [14].Liu Q, Yuan H, Hamzaoui R, Su H, Hou J, and Yang H, “Reduced reference perceptual quality model with application to rate control for video-based point cloud compression,” IEEE Transactions on Image Processing, vol. 30, pp. 6623–6636, 2021. [DOI] [PubMed] [Google Scholar]
- [15].Viola I. and Cesar P, “A reduced reference metric for visual quality evaluation of point cloud contents,” IEEE Signal Processing Letters, vol. 27, pp. 1660–1664, 2020. [Google Scholar]
- [16].Yue G, Cheng D, Li L, Zhou T, Liu H, and Wang T, “Semi-supervised authentically distorted image quality assessment with consistency-preserving dual-branch convolutional neural network,” IEEE Transactions on Multimedia, vol. 25, pp. 6499–6511, 2023. [Google Scholar]
- [17].Tao W, Jiang G, Jiang Z, and Yu M, “Point cloud projection and multi-scale feature fusion network based blind quality assessment for colored point clouds,” in Proceedings of the 29th ACM International Conference on Multimedia, 2021, pp. 5266–5272. [Google Scholar]
- [18].Liu Q, Yuan H, Su H, Liu H, Wang Y, Yang H, and Hou J, “PQA-Net: Deep no reference point cloud quality assessment via multi-view projection,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 31, no. 12, pp. 4645–4660, 2021. [Google Scholar]
- [19].Liu Y, Yang Q, Xu Y, and Yang L, “Point cloud quality assessment: Dataset construction and learning-based no-reference metric,” ACM Transactions on Multimedia Computing, Communications and Applications, vol. 19, no. 2s, pp. 1–26, 2023. [Google Scholar]
- [20].Yan J, Fang Y, Du R, Zeng Y, and Zuo Y, “No reference quality assessment for 3D synthesized views by local structure variation and global naturalness change,” IEEE Transactions on Image Processing, vol. 29, pp. 7443–7453, 2020. [Google Scholar]
- [21].Tibshirani R, “Regression shrinkage and selection via the lasso,” Journal of the Royal Statistical Society: Series B (Methodological), vol. 58, no. 1, pp. 267–288, 1996. [Google Scholar]
- [22].Smola AJ and Scholkopf B, “A tutorial on support vector regression,” Statistics and Computing, vol. 14, no. 3, pp. 199–222, 2004. [Google Scholar]
- [23].Fang Y, Yan J, Du R, Zuo Y, Wen W, Zeng Y, and Li L, “Blind quality assessment for tone-mapped images by analysis of gradient and chromatic statistics,” IEEE Transactions on Multimedia, vol. 23, pp. 955–966, 2020. [Google Scholar]
- [24].Fang Y, Yan J, Li L, Wu J, and Lin W, “No reference quality assessment for screen content images with both local and global feature representation,” IEEE Transactions on Image Processing, vol. 27, no. 4, pp. 1600–1610, 2017. [DOI] [PubMed] [Google Scholar]
- [25].Yue G, Cheng D, Zhou T, Hou J, Liu W, Xu L, Wang T, and Cheng J, “Perceptual quality assessment of enhanced colonoscopy images: A benchmark dataset and an objective method,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 33, no. 10, pp. 5549–5561, 2023. [Google Scholar]
- [26].Mekuria R, Laserre S, and Tulvan C, “Performance assessment of point cloud compression,” in 2017 IEEE Visual Communications and Image Processing (VCIP), 2017, pp. 1–4. [Google Scholar]
- [27].Mekuria R, Blom K, and Cesar P, “Design, implementation, and evaluation of a point cloud codec for tele-immersive video,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 27, no. 4, pp. 828–842, 2016. [Google Scholar]
- [28].Wang Z, Bovik AC, Sheikh HR, and Simoncelli EP, “Image quality assessment: from error visibility to structural similarity,” IEEE Transactions on Image Processing, vol. 13, no. 4, pp. 600–612, 2004. [DOI] [PubMed] [Google Scholar]
- [29].Yue G, Hou C, Gu K, Zhou T, and Zhai G, “Combining local and global measures for dibr-synthesized image quality evaluation,” IEEE Transactions on Image Processing, vol. 28, no. 4, pp. 2075–2088, 2018. [DOI] [PubMed] [Google Scholar]
- [30].Wang Z, Simoncelli EP, and Bovik AC, “Multiscale structural similarity for image quality assessment,” in The Thrity-Seventh Asilomar Conference on Signals, Systems & Computers, 2003, vol. 2, 2003, pp. 1398–1402. [Google Scholar]
- [31].Liu Q, Su H, Duanmu Z, Liu W, and Wang Z, “Perceptual quality assessment of colored 3D point clouds,” IEEE Transactions on Visualization and Computer Graphics, vol. 29, no. 8, pp. 3642–3655, 2023. [DOI] [PubMed] [Google Scholar]
- [32].Sheikh HR and Bovik AC, “Image information and visual quality,” IEEE Transactions on Image Processing, vol. 15, no. 2, pp. 430–444, 2006. [DOI] [PubMed] [Google Scholar]
- [33].Yang Q, Chen H, Ma Z, Xu Y, Tang R, and Sun J, “Predicting the perceptual quality of point cloud: A 3D-to-2D projection-based exploration,” IEEE Transactions on Multimedia, vol. 23, pp. 3877–3891, 2020. [Google Scholar]
- [34].Meynet G, Nehm Y, Digne J, and Lavou G, “PCQM: A full-reference quality metric for colored 3d point clouds,” in 2020 Twelfth International Conference on Quality of Multimedia Experience (QoMEX), 2020, pp. 1–6. [Google Scholar]
- [35].Alexiou E. and Ebrahimi T, “Towards a point cloud structural similarity metric,” in 2020 IEEE International Conference on Multimedia & Expo Workshops (ICMEW), 2020, pp. 1–6. [Google Scholar]
- [36].Diniz R, Freitas PG, and Farias MC, “Point cloud quality assessment based on geometry-aware texture descriptors,” Computers & Graphics, vol. 103, pp. 31–44, 2022. [Google Scholar]
- [37].Xu Y, Yang Q, Yang L, and Hwang J-N, “EPES: Point cloud quality modeling using elastic potential energy similarity,” IEEE Transactions on Broadcasting, vol. 68, no. 1, pp. 33–42, 2021. [Google Scholar]
- [38].Yang Q, Zhang Y, Chen S, Xu Y, Sun J, and Ma Z, “MPED: Quantifying point cloud distortion based on multiscale potential energy discrepancy,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 45, no. 5, pp. 6037–6054, 2023. [DOI] [PubMed] [Google Scholar]
- [39].Lu Z, Huang H, Zeng H, Hou J, and Ma K-K, “Point cloud quality assessment via 3D edge similarity measurement,” IEEE Signal Processing Letters, vol. 29, pp. 1804–1808, 2022. [Google Scholar]
- [40].Viola I, Subramanyam S, and Cesar P, “A color-based objective quality metric for point cloud contents,” in 2020 Twelfth International Conference on Quality of Multimedia Experience (QoMEX). IEEE, 2020, pp. 1–6. [Google Scholar]
- [41].Zhou W, Yue G, Zhang R, Qin Y, and Liu H, “Reduced-reference quality assessment of point clouds via content-oriented saliency projection,” IEEE Signal Processing Letters, vol. 30, pp. 354–358, 2023. [Google Scholar]
- [42].Tu R, Jiang G, Yu M, Luo T, Peng Z, and Chen F, “V-PCC projection based blind point cloud quality assessment for compression distortion,” IEEE Transactions on Emerging Topics in Computational Intelligence, vol. 7, no. 2, pp. 462–473, 2023. [Google Scholar]
- [43].Liu Y, Yang Q, Xu Y, and Yang L, “Point cloud quality assessment: Dataset construction and learning-based no-reference metric,” ACM Transactions on Multimedia Computing, Communications and Applications, vol. 19, no. 2s, pp. 1–26, 2023. [Google Scholar]
- [44].Su H, Liu Q, Liu Y, Yuan H, Yang H, Pan Z, and Wang Z, “Bitstream-based perceptual quality assessment of compressed 3D point clouds,” IEEE Transactions on Image Processing, vol. 32, pp. 1815–1828, 2023. [DOI] [PubMed] [Google Scholar]
- [45].Guede C, Andrivon P, Marvie J-E, Ricard J, Redmann B, and Chevet J-C, “V-PCC performance evaluation of the first MPEG point codec,” SMPTE Motion Imaging Journal, vol. 130, no. 4, pp. 36–52, 2021. [Google Scholar]
- [46].Friedman JH, Bentley JL, and Finkel RA, “An algorithm for finding best matches in logarithmic expected time,” ACM Transactions on Mathematical Software (TOMS), vol. 3, no. 3, pp. 209–226, 1977. [Google Scholar]
- [47].Alexiou E, Ebrahimi T, Bernardo MV, Pereira M, Pinheiro A, Cruz LADS, Duarte C, Dmitrovic LG, Dumic E, Matkovics D. et al. , “Point cloud subjective evaluation methodology based on 2D rendering,” in 2018 Tenth International Conference on Quality of Multimedia Experience (QoMEX), 2018, pp. 1–6. [Google Scholar]
- [48].Rusu RB and Cousins S. (Apr. 2, 2020) Compute underlying surface’s normal and curvature in local neighborhoods (PCL). [Online]. Available: https://pointclouds.org/ [Google Scholar]
- [49].Winkler S, Kunt M, and van den Branden Lambrecht CJ, “Vision and video: models and applications,” in Vision Models and Applications to Image and Video Processing. Springer, 2001, pp. 201–229. [Google Scholar]
- [50].ITU, “Parameter values for the hdtv standards for production and international programme exchange,” Recommendation BT.709–6, 2015. [Google Scholar]
- [51].Antkowiak J, “Final report from the video quality experts group on the validation of objective models of video quality assessment,” March 2000. [Google Scholar]
- [52].Sedgwick P, “Pearsons correlation coefficient,” BMJ, vol. 345, e4483, 2012. [Google Scholar]
- [53].Sheskin D, “Spearmans rank-order correlation coefficient,” Handbook of Parametric and Nonparametric Statistical Procedures, pp. 1353–1370, 2007. [Google Scholar]
- [54].Natarajan BK, “Sparse approximate solutions to linear systems,” SIAM Journal on Computing, vol. 24, no. 2, pp. 227–234, 1995. [Google Scholar]
- [55].Hamo Y. and Markovitch S, “The compset algorithm for subset selection,” in Proceedings of the 19th International Joint Conference on Artificial Intelligence, 2005, pp. 728–733. [Google Scholar]
- [56].Donoho DL and Elad M, “Optimally sparse representation in general (nonorthogonal) dictionaries via l1 minimization,” Proceedings of the National Academy of Sciences, vol. 100, no. 5, pp. 2197–2202, 2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57].Abouelaziz I, El Hassouni M, and Cherifi H, “Blind 3D mesh visual quality assessment using support vector regression,” Multimedia Tools and Applications, vol. 77, no. 18, pp. 24365–24386, 2018. [Google Scholar]
- [58].Tezcan J. and Cheng Q, “A nonparametric characterization of vertical ground motion effects,” Earthquake Engineering & Structural Dynamics, vol. 41, no. 3, pp. 515–530, 2012. [Google Scholar]
- [59].Vapnik V, The Nature of Statistical Learning Theory. Springer Science & Business Media, New York, 1999. [Google Scholar]
- [60].Platt J, “Sequential minimal optimization: A fast algorithm for training support vector machines,” Technical Report MSR-TR-98-14, 1998. [Google Scholar]
- [61].Alexiou E, Viola I, Borges TM, Fonseca TA, De Queiroz RL, and Ebrahimi T, “A comprehensive study of the rate-distortion performance in mpeg point cloud compression,” APSIPA Transactions on Signal and Information Processing, vol. 8, p. e27, 2019. [Google Scholar]
- [62].MPEG 3DG. (2019) V-PCC test model v7. [Online]. Available: http://mpegx.int-evry.fr/software/MPEG/PCC/TM/mpeg-pcc-tmc2.git
- [63].Gramfort A, Pedregosa F, Grisel O, and Varoquaux G. (2021) Lasso code source. [Online]. Available: https://github.com/scikit-learn/scikit-learn [Google Scholar]
- [64].Chang C-C and Lin C-J, “LIBSVM: a library for support vector machines,” ACM Transactions on Intelligent Systems and Technology (TIST), vol. 2, no. 3, pp. 1–27, 2011. [Google Scholar]
- [65].Liu T-J, Lin W, and Kuo C-CJ, “Image quality assessment using multi-method fusion,” IEEE Transactions on Image Processing, vol. 22, no. 5, pp. 1793–1807, 2012. [DOI] [PubMed] [Google Scholar]
- [66].Yeganeh H. and Wang Z, “Objective quality assessment of tone-mapped images,” IEEE Transactions on Image Processing, vol. 22, no. 2, pp. 657–667, 2013. [DOI] [PubMed] [Google Scholar]
- [67].Viola I. and Cesar P. (2020) PCM_RR. [Online]. Available: https://github.com/cwi-dis/PCM_RR [Google Scholar]