Abstract
This letter proposes a novel method, multi-input, multi-output neuronal mode network (MIMO-NMN), for modeling encoding dynamics and functional connectivity in neural ensembles such as the hippocampus. Compared with conventional approaches such as the Volterra-Wiener model, linear-nonlinear-cascade (LNC) model, and generalized linear model (GLM), the NMN has several advantages in terms of estimation accuracy, model interpretation, and functional connectivity analysis. We point out the limitations of current neural spike modeling methods, especially the estimation biases caused by the imbalanced class problem when the number of zeros is significantly larger than ones in the spike data. We use synthetic data to test the performance of NMN with a comparison of the traditional methods, and the results indicate the NMN approach could reduce the imbalanced class problem and achieve better predictions. Subsequently, we apply the MIMO-NMN method to analyze data from the human hippocampus. The results indicate that the MIMO-NMN method is a promising approach to modeling neural dynamics and analyzing functional connectivity of multi-neuronal data.
1. Introduction
Currently, three types of methods are widely used in terms of modeling neural systems. The first type is the Volterra-Wiener model (Marmarelis & Marmarelis, 1978) and its variants, such as principal dynamic modes (PDM) (Marmarelis et al., 2013, 2014) and neuronal modes (NM) analysis (French & Marmarelis, 1995; Marmarelis & Orme, 1993; Mitsis, French, Höger, Courellis, & Marmarelis, 2007; Zanos et al., 2008). The PDM and NM modeling approaches are very compact by finding a parsimonious number of linear filters or basis functions. In addition, the PDM and NM methods are capable of relating the frequency-domain representations to well-known neural rhythms during specific sensory, motor, and cognitive functions (Kang, Escudero, Shin, Ifeachor, & Marmarelis, 2015; Marmarelis et al. 2013, 2014; Sandler et al., 2015a, 2015b; Geng et al., 2018). However, these two methods use least squares for estimating the respective models that result in estimation biases due to nongaussian prediction errors for spike-output systems.
The second type of method is generalized linear modeling (GLM) (Paninski 2004; Truccolo, Eden, Fellows, Donoghue, & Brown, 2005; Gerwinn, Bethge, Macke, & Seeger, 2008; Gerwinn, Macke, & Bethge, 2010; Okatan, Wilson, & Brown, 2005; Stevenson, Rebesco, Miller, & Körding, 2008; Stevenson et al., 2009; Song et al., 2007, 2009, 2013, 2015), which would mitigate the nongaussian prediction errors by introducing a link function between the spike output and the linear predictor. However, the limitation of this approach is the “imbalanced class/data problem” (King & Zeng, 2001; He, Bai, Garcia, and Li, 2008), because the number of zeros significantly outnumbers the spikes in the output data. The objective function of the GLM method, which is often expressed as the log loss or cross-entropy function, is not well suited for spike output data analysis because of the estimation biases caused by imbalanced ones and zeros (King & Zeng, 2001).
The imbalanced class problem remains a challenge in machine learning and in the data mining community, and some approaches, such as sampling and cost-sensitive methods, are utilized to alleviate this problem (Chawla, Japkowicz, & Kotcz, 2004; Galar, Fernandez, Barrenechea, Bustince, & Herrera, 2012; He, Bai, Garcia, & Li, 2008; Kubat, & Matwin, 1997; López, Fernández, García, Palade, & Herrera, 2013). However, it would be difficult to directly apply these methods for spike train data because of the intrinsic nonlinear dynamic properties.
The third type of the methods is the linear-nonlinear cascade (LNC) model, which consists of the linear-nonlinear-Poisson (LNP) models for spike count data and linear-nonlinear-Bernoulli (LNB) models for spike train data (Aljadeff, Lansdell, Fairhall, & Kleinfeld, 2016; Bialek & van Steveninck 2005; Chichilnisky 2001; McFarland, Cui, & Butts, 2013; Pillow & Simoncelli, 2006; Schwartz, Pillow, Rust, & Simoncelli, 2006; Sharpee, Rust, & Bialek, 2004; Simoncelli, Paninski, Pillow, & Schwartz, 2004; Theis, Chagas, Arnstein, Schwarz, & Bethge, 2013; Williamson, Sahani, & Pillow, 2015; Meyer, Williamson, Linden, & Sahani, 2017). Linear-nonlinear cascade (LNC) models have the gaussian input assumption, so they are not suitable for inputs with spike train data.
These three types of methods are tightly related to each other. It has been shown that the LNC models with spike-triggered average (STA) or spike-triggered covariance (STC) estimations are essentially equivalent to Volterra-Wiener models (Sandler & Marmarelis, 2015; Meyer et al., 2017). However, if LNC models are estimated with the maximum likelihood method, they are equivalent to the GLM approach (Williamson et al., 2015).
To develop neuroprostheses that mimic some aspect of neural function and restore impaired regions, multi-input, multi-output (MIMO) dynamic nonlinear models are required to extract predictive neuronal relationships from MIMO spike train data (Berger et al., 2001, 2011, 2012; Berger, Song, Chan, & Marmarelis, 2010; Hampson et al., 2018). In modeling studies of multi-neuronal systems, the Volterra-Wiener approaches are commonly used (Marmarelis et al., 2013, 2014; Sandler et al., 2015a, 2015b, 2018; Zanos et al., 2008). GLM approaches and their variants have also been also explored (Berger et al., 2011, 2012; Berger, Song, Chan, & Marmarelis, 2010; Hampson et al., 2018; Song et al., 2007, 2009, 2013, 2015; Gerwinn et al., 2008, 2010; Okatan et al., 2005; Stevenson et al., 2008, 2009; Paninski, 2004).
MIMO models tend to overfit the data since the number of parameters could grow dramatically with the number of inputs and outputs. Due to government regulations and patients’ health concerns, the multi-neuronal activities recorded in the human brain are usually very short, which would exacerbate the overfitting problem. Therefore, minimizing the number of free parameters in the MIMO model is critical for reducing overfitting. This task can be achieved with two general approaches. One is the search for a parsimonious representation of the neuronal dynamics by the MIMO model. Some techniques have been developed such as regularizations (Song et al., 2013) and kernel expansion techniques (Marmarelis et al., 2013, 2014). Another complementary approach to reduce overfitting is via selecting the minimum number of input neurons that are functionally connected to the output neurons of interest within the available multi-neuronal recordings. Finding the important input neurons that are functionally connected to output neurons would help to eliminate the unnecessary input-output connections and reduce the number of parameters of the MIMO model. Here, we adopt the definition of “functional connectivity” as the minimum input-output connections that can adequately predict the activity of each output neuron (Aertsen, Gerstein, Habib, & Palm, 1989; Stevenson et al., 2008). Linear methods such as cross-correlograms have been used to investigate the interconnections between input-output neurons (Aertsen et al., 1989; Brody, 1999; Perkel, Gerstein, & Moore, 1967). In addition, the GLM methods with priors or regularizations could also serve to identify functional connectivity (Gerwinn et al., 2008, 2010; Okatan et al., 2005; Song et al., 2013; Stevenson et al., 2008, 2009; Paninski, 2004). However, the GLM-based models could be biased by the imbalanced class problem we already noted.
Recently, artificial neural network (ANN)–based methods have been explored as a new approach to model realistic neural systems (Prenger, Wu, David, & Gallant, 2004; Saggar, Meriçli, Andoni, & Miikkulainen, 2007; Geng & Marmarelis 2015, 2017; Benjamin et al., 2018). However, these models do not have binary spike train data as the inputs or the outputs. Neuronal mode network (NMN) has been proposed to model the neural system’s binary spike train data in the hippocampus system (Geng et al., 2018) and analyze CA3-CA1 signal transformation in the hippocampus. The initial results showed that NMN is capable of compactly representing the neural dynamics and nonlinearities. However, the NMN method has only been applied in the analysis of single-input and single-output (SISO) data, which limited its applications in modeling MIMO neural ensembles such as the hippocampus.
This letter extends previous work on NMN. There are four major contributions. First, we investigate the shortcomings of current spike train data modeling methods, especially the imbalanced class problem. Second, we use synthetic data to show that the NMN model could potentially reduce the imbalanced class problem and achieve better estimation results. Third, we propose a novel MIMO-NMN modeling approach for analyzing the encoding dynamics of the neural ensembles and applied the MIMO-NMN model for predicting neural activities in the human hippocampal CA3-CA1 regions. Finally, our analysis results from human hippocampus data indicate that the Ising cost function of MDM provides a metric to measure the connectivity strength for each input-output neuronal pair that can easily yield a functional connectivity map of the neuronal ensemble.
The letter is presented as follows. We review spike train modeling methods and the imbalanced data problem in section 2. Then we briefly describe the methodology of the NMN and its cost function in section 3. In section 4, we describe how to construct the MIMO-NMN model. In section 5, we use simulated data to test the efficacy of NMN and compare the results with the traditional NM and GLM methods. In addition, we apply the MIMO-NMN to data collected intraoperatively in the human hippocampus in section 6. Finally, in section 7, we discuss the results and draw conclusions.
2. Spike Train Data Modeling Methods and the Imbalanced Class Problem
For a SISO neural system with both input and output binary spike trains, let x(n) = [x(n − M + 1),...,x(n)] represent the input vector with length M that contributes the probability that a spike occurs at time n. Then the spiking probability is defined as
| (2.1) |
where is the nonlinear static transformation function. A naive way to represent the model is to have a weighted summation of x(n) followed by a nonlinear function (Theis et al., 2013). However, this approach tends to cause overfitting problems when only limited data are available. A more compact approach is to use basis functions and linear filters to represent the model dynamics (Marmarelis et al., 2013, 2014; Song et al., 2013), so the overall number of parameters could be largely reduced. Then the static transformation function can be written as
| (2.2) |
where {uj(n)} are the outputs of the linear filters
| (2.3) |
and bj is the jth basis function.
Directly applying least squares estimation (LSE) to minimize the errors between F[x(n)] and binary output y(n) would cause biases because the errors would not follow gaussian distribution. Therefore, the traditional PDM/NM methods that use LSE would not be optimal for spike train data analysis. Note that the LNP/LNB models with STA/STC estimation could be biased for the same reason since they are essentially equivalent to Volterra-Wiener models with LSE (Sandler & Marmarelis, 2015).
To solve this problem, the GLM introduces the function g(.) to link the spiking probability p(n) with F[x(n)] as follows:
| (2.4) |
Thus, the spiking probability p(n) can be expressed as
| (2.5) |
Common choices of the link function for spike train data would be the logit function (Theis et al., 2013) and probit function (Song et al., 2013). Using the logit link function, the spiking probability is
| (2.6) |
Similarly, with the probit link function, the spiking probability can be expressed as
| (2.7) |
Equations 2.6 and 2.7 are practically identical since the outputs are very similar given the same inputs.
Following the GLM approach, the parameters in F(.) are optimized by maximum likelihood estimation (MLE) (King & Zeng, 2001; Truccolo et al., 2005; Williamson et al., 2015; Meyer et al., 2017), where the log-likelihood function is defined as
| (2.8) |
The above function is often termed a cross-entropy function or a log-loss function in the machine learning field. It should be noted that the parameters estimated by MLE are biased when the sample size is small, and the bias is magnified by the imbalanced class of the data (King & Zeng, 2001).
Here is an intuitive way to understand the imbalanced class problem. By minimizing the cross-entropy function in equation 2.8, the MLE approach tries to find a hyperplane that best separates the zeros from ones. In regions where ones and zeros are nonseparable, the hyperplane would prefer to classify ones as zeros. The reason is straightforward: since the zeros have a higher density than ones for imbalanced data, classifying ones as zeros would cause fewer errors and a smaller cross-entropy function. As a result, the spiking probability p(n) is underestimated, and the estimated parameters in are biased (King & Zeng, 2001).
For a MIMO system with D inputs and K outputs, the MIMO model can be decomposed of D multi-input single-output models (MISO). The spiking probability for kth output is
| (2.9) |
Then the static nonlinear transformation function can be represented as
| (2.10) |
Note that in equation 2.10, we consider only the pairwise interactions between each element in {ui, j}, where ui, j is the output of the jth basis function that corresponds to the ith input.
Finally, we can represent the spiking probability of the kth output with link function gk:
| (2.11) |
The cross-entropy function for the MIMO GLM model is
| (2.12) |
Similarly, the parameters of F(.) are optimized by the MLE method, which suffers the imbalanced class problem as well. In addition, as we can see in equation 2.10, the number of parameters that need to be estimated grow exponentially with the number of inputs D, the number of output K, the number of basis functions L, and the model order Q, which would easily lead to overfitting problems when limited data are available. To reduce the overfitting problems, regularization techniques are commonly used by adding penalty terms to the cross-entropy function in equations 2.8 and 2.12.
3. Review of NMN
We briefly review the architecture of NMN (Geng et al., 2018).
NMN is composed of two modules: (1) neuronal modes (NMs), which are weighted combinations of Laguerre basis functions and act as a linear filter bank, and (2) multidimensional mapping (MDM), which nonlinearly transforms the NM outputs into spiking probabilities. The NMs of the system can be represented as
| (3.1) |
where {bj} are the discrete Laguerre functions (DLFs; Marmarelis, 2004), α is the hyperparameter that determines the exponential declining rate of the DLFs, and L is the number of the DLFs. Since the number of NMs is smaller than the number of DLFs, the set of NMs is a parsimonious representation of the system dynamics.
The outputs of the NMs can be expressed as
| (3.2) |
The output of the NMN is defined as the spiking probability at time n:
| (3.3) |
where is the nonlinear function of MDM that follows Bayes’ rule, as shown in equation A.7 in the appendix. The construction details of MDM are described in the appendix. The training process follows the simulated annealing algorithm described in Geng et al. (2018).
The goal of optimizing the NMN is to find a set of optimal NMs that would separate the spiking from the non-spiking events in the MDM. The parameters that need to be optimized are NM-related parameters: {wj,h} and α. The cost function is based on Ising energy (Ising, 1925; Wu, 1982), which is defined as
| (3.4) |
where β is the normalization factor and g(i) is the spiking probability at the ith pixel in MDM, which is defined in equation A.7. The notation represents the bonds formed by neighboring pixels i and j in MDM. This Ising energy cost function encourages the clustering of spiking events to form a trigger region (TR) and discourages the mix between the spiking and non-spiking events (Geng et al., 2018).
MDM together with the Ising cost function also reduces the imbalanced class problem of spike train data. Taking the MDM in Figure 3 as an example, there are dozens or even hundreds of non-spiking events inside a single blue pixel, while there are only one or several spiking events inside a single red pixel. However, when calculating the cost function in equation 3.4, only the spiking probability of the pixels would contribute to the cost function rather than the absolute number of non-spiking and spiking events. Thus, the information contained by redundant zeros is compressed, and the information contained by rare spikes is augmented. And due to this property, the required number of spikes for training is also significantly reduced. The NMN method seeks to find a set of NMs that yield an optimal structure of the MDM instead of directly maximizing the prediction performance (as traditional learning algorithms do), which would suffer from the imbalanced class problem.
Figure 3:
NM method estimation results of the data with noise level 0.35. (a) The estimated NMs. (b) The estimated MDM with grid resolution 40 × 40.
The evaluation of the performance of the NMN is based on the receiver operating characteristic (ROC) curve, which is commonly used for evaluating model performance with imbalanced class data (Chawla et al., 2004; Galar et al., 2012; He et al., 2008; Kubat, & Matwin, 1997; López et al., 2013), as well as spike train data (Marmarelis et al., 2014; Sandler et al., 2015a, 2015b; Sandler & Marmarelis, 2015; Igarashi, Lu, Colgin, Moser, & Moser, 2014). The ROC curve is plotted for the true-positive ratio (TPR) against the false-positive ratio (FPR) by changing the threshold value. The TPR and FPR are defined as
| (3.5) |
where Ntp and Nfp are the number of true positives and false positives, Np is the number of spikes in real data, and Nz is the number of zeros.
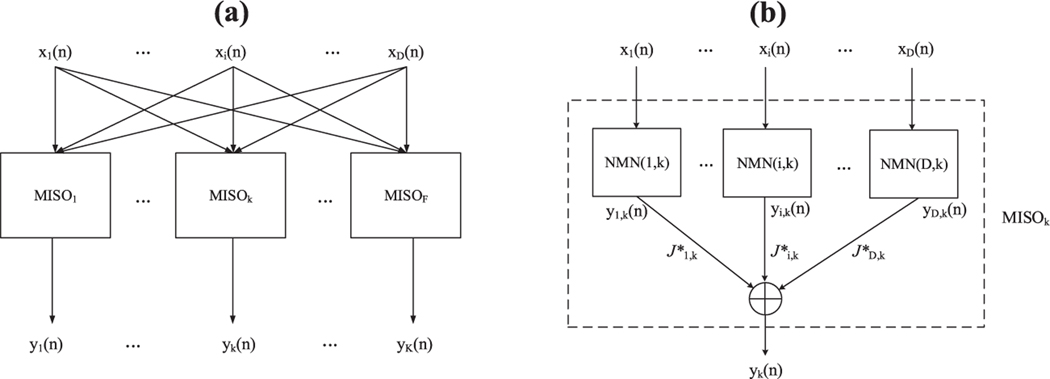
4. Multi-Input, Multi-Output NMN
If the input and output neuronal pair has no causal relationship, then it is impossible to find a set of optimal NMs that can lead to separation between spiking (ones) and non-spiking events (zeros) in MDM. In that case, the MDM after optimization would still be largely blurred, and thus the Ising cost function would be around zero. Therefore, the value of Ising cost function in equation 3.4 after optimization could serve as an indicator of how strongly the input and output neurons are functionally connected. Inspired by this observation, we propose the MIMO-NMN model.
Assume that the MIMO model has D inputs and K outputs. Then, after the single-input, single-output (SISO) NMN analysis of all pairs, we have D × K pairwise models, which need to be combined for MIMO predictions. As illustrated in Figure 1, since the MIMO model can be divided into K MISO models, the first step is to construct a MISO model using the corresponding pairwise NMN models. As described in section 2, the cost function of MDM could serve an indicator of the connection strength between the input and output neurons, so the output of the MISO model could be obtained by the weighted sum of the SISO outputs, where the weights are the values of the cost function of each corresponding NMN model. For example, if Ji,k is around zero, indicating the connection between the (i, k) neuron pair is weak, then the input neuron i would have very little or no effect on the output neuron k. Otherwise, the input neuron should have a strong effect on the output neuron. Therefore, the output of the MISOk can be represented by
| (4.1) |
where is the normalized cost function value of NMN(i, k). Since is around zero for the weakly connected input and output pairs, we can remove these weak connections and associated parameters without significantly affecting the MIMO prediction outcomes.
Figure 1:
Architecture of the MIMO model. (a) The MIMO model that has D inputs and K outputs can be divided into several MISO models. (b) In each MISO model, the output yk can be calculated by the weighted sum of the outputs from the SISO NMN model.
5. Simulation Results
We use the data generated from the simulated LNB cascade system in Figure 2 to evaluate the performance of the proposed NMN approach relative to the traditional NM and GLM methods. The simulated system follows the architecture of a typical linear-nonlinear-Bernoulli (LNB) cascade model (Williamson et al., 2015). It consists of two distinct linear filters that are generated with Laguerre basis functions. The parameters of basis function α and weight matrix W are shown in Table 1. The outputs of liner filters are nonlinearly interacted, and the nonlinear function is
| (5.1) |
Finally, the output spike train data are generated with a Bernoulli process. To explore the model’s robustness, independent spurious spikes are added to the output spikes as noise to the output. The noise represents the effects from other input neurons that are not observable in the experiment. We define the noise level as
Figure 2:
The simulated LNB cascade system that generated the synthetic data for model evaluations. The system consists of two linear filters, a nonlinear function , and a Bernoulli process to generate spikes. The corresponding MDM is shown on the right.
Table 1:
Exact and Trained Values of the Parameters.
| Symbol | Exact Values | Traditional NM Method | NMN |
|---|---|---|---|
| α | 0.7 | 0.7 | 0.72 |
| W |
We have generated the data with different noise levels (0, 0.1, 0.35, 0.5). For each noise level, we generate training data with length 10,240 and test data with length 2048. We keep the firing ratio at 1% to 3% to represent the imbalanced ones and zeros. To simplify the comparisons, we assume that the NM and GLM are able to find the best hyperparameters: L = 5 and α = 0.7.
First, we analyzed the training data with noise level 0.35 using the traditional NM method via least-squares estimation and singular value decomposition (Marmarelis & Orme, 1993). The estimated NMs and MDM from the data are shown in Figure 3, and the estimated α and NM weight matrix are shown in Table 1. Then we use the NMN method to analyze the same data with the simulated annealing (SA) optimization algorithm (Geng et al., 2018). The detailed tracking plots of the cost function J and α during the training process are shown in Figures 4a and 4b. The obtained NMs and MDM are shown in Figures 4c and 4d. The estimated NM weights are summarized in Table 1. By comparing estimation results in Figures 3 and 4 with the LNB system in Figure 2, we can see that the NMN method gives much more accurate estimations of the linear filters as well as the MDM. The weight matrix estimated by NMN is closer to the exact values than the NM method, as shown in Table 1.
Figure 4:
NMN method estimation results of data with noise level 0.35. (a,b) The tracking plots of the cost function and Laguerre parameter α during the training process. (c,d) The estimated NMs and MDM when the training resolution is 40 × 40.
It is important to explore the effects of the MDM resolution in terms of the training and evaluation process. As shown in Figure 5, each row represents the results using different resolution during the training process, ranging from 10 × 10 to 100 × 100. As we can see, the estimation is poor when the resolution is small (below 20 × 20), as MDM with such small resolution cannot accurately represent the complicated system nonlinearity. When the resolution is larger than 80 × 80, the estimation is also poor because of overfitting. When the resolution is between 40 × 40 and 60 × 60, the estimation results are fairly accurate and the differences are insignificant.
Figure 5:
Exploring the effects of different MDM resolutions. Each row represents the estimated NM, MDM, and ROC plots using different resolution during the training process.
We also compare the NMN (Geng et al., 2018), NM (Marmarelis & Orme, 1993), and GLM (Song et al., 2009) by analyzing the same data set. The detailed predictions for the test data set with noise level 0.35 are shown in Figure 6, indicating that the NMN method yields the best predictions among these three methods. For example, NMN predicts the smallest spiking probabilities for zeros during the 1050 to 1100 ms in Figure 6a, which would reduce the false positives. It also predicts larger spiking probabilities for spikes than the other two methods do (see 1130 to 1150 ms and 1320 to 1350 ms in Figure 6a). The ROC curve of NMN is uniformly better than the other two methods in Figure 6b, especially for low FPR. The TPR reaches 0.6, while the FPR is only 0.02 for the ROC curve of NMN, indicating the robustness of the NMN method since around one-third of the output spikes are spurious noise. In addition, we compare the ROC results under other noise levels (0, 0.1, 05), as shown in Figure 7. Overall, NMN yields the best performances across different noise levels.
Figure 6:
Comparison of model predictions of the out-of-sample data set (noise level = 0.35) between the NM, GLM, and NMN methods. (a) Predictions of the spiking probabilities. (b) ROC curves.
Figure 7:
Comparison of model predictions of out-of-sample data set between the NM, GLM, and NMN methods for ROC curves under noise levels 0, 0.1, and 0.5.
6. Analysis of Human Hippocampus Data
Multi-neuronal data were recorded from the CA3 and CA1 regions of the human hippocampus intraoperatively in medically refractory focal epilepsy patients at Wake Forest Baptist Medical Center. All procedures were reviewed and approved by the Institutional Review Board of Wake Forest University, in accordance with the National Institutes of Health. Patients underwent preoperative imaging to determine intraoperative electrode placement. The electrodes consisted of FDA-approved shaft electrodes capable of single-unit neuronal recording and field potential recording (Ad-Tech Medical Instrumentation Corporation, Racine, WI). Intraoperative placement of the depth electrodes was performed using either a stereotactic head frame (CRW Precision Arc, Integra Life Sciences, Plainsboro, NJ) or frameless stereotactic system (VarioGuide, Brainlab AG, Feldkirchen, Germany) at the discretion of the operating surgeon. Hippocampal electrode placement was targeted to penetrate the head of the hippocampus perpendicular to its long axis in order to record neuronal activity within the CA3 and CA1 subfields. In this letter, we present the results of NMN analysis of data only from patient during the intraoperative performance of a delayed match-to-sample (DMS) task.
The DMS trials were initiated by the examiner, who manually triggered the presentation of a nonverbalizable image, constituting the sample presentation (SP) phase of the task. Completion of the SP task required the patient to touch the presented image, designated as the sample response (SR) phase. The SR phase then initiated the delay interval phase of the trial during which the screen was blank for 5 to 15 seconds, randomly determined on a trial-by-trial basis. The delay interval was followed by the match presentation (MP) phase of the task, which consisted of the simultaneous display of two to seven images displayed at randomly selected spatial locations on the screen, one of which was the sample image. Touching either the previously presented image or another image was designated a match response (MR). Correct responses produced a reward tone followed by a blank screen. Incorrect responses caused by touching one of the nonmatch (distractor) images, which constituted a nonmatch response, led to an error tone followed by a blank screen. Trials were separated by 5 seconds prior to initiation of the next trial. For patient 2, 14 trials were recorded with the correct DMS response and 22 trials with the incorrect response. Spike train data were recorded from seven CA3 neurons and eight CA1 neurons during the DMS task. We analyzed the data during the 7 second period after SP, with a bin size of 5 ms. The average firing rate ranges from 0.005 to 0.03, which indicates a strong imbalanced class problem in the data set.
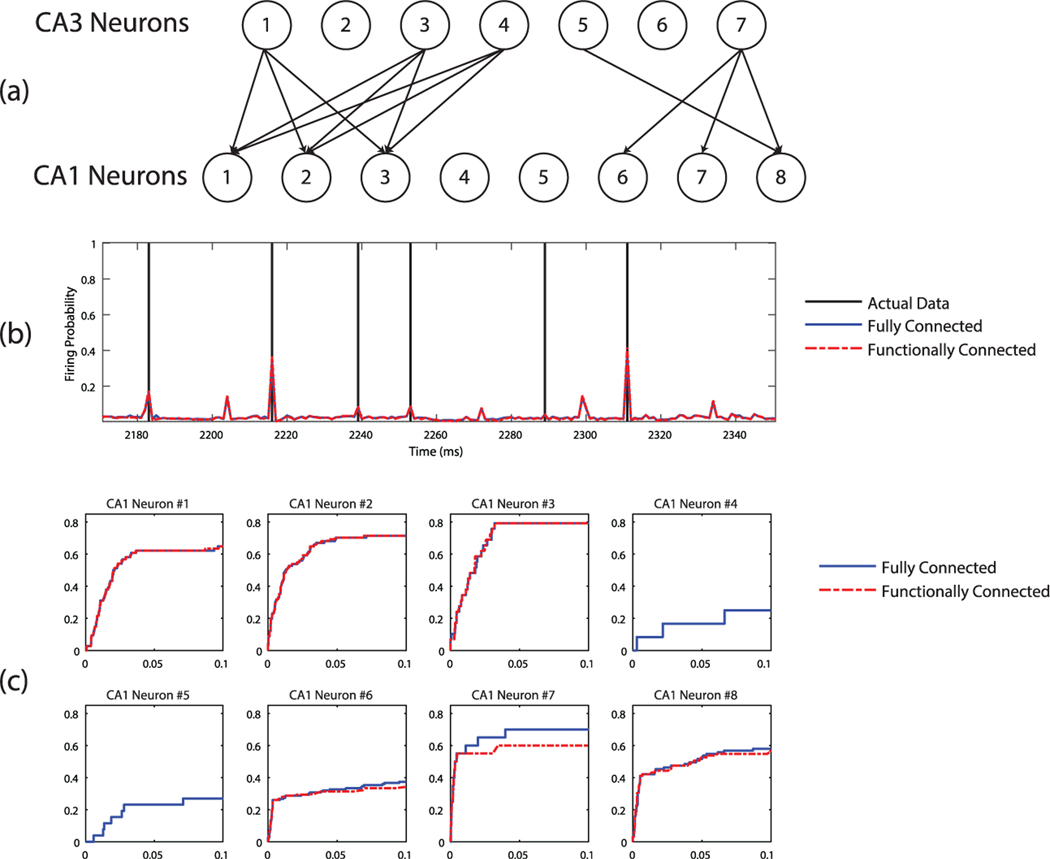
We applied the Ising cost function approach to determine the functional connectivity between the CA3 neurons as inputs and the CA1 neurons as outputs. Fifty-six neuronal input-output pairs were analyzed. For the correct DMS trials, we used 10 of the 14 correct DMS trials as the training data and the remaining 4 as the test data. For the incorrect DMS trials, we use 16 of 22 as the training data set and the remaining 6 as the test data. Since the estimation results are not sensitive to L within the range from 3 to 7, we selected L = 5 for the NMN. We found that a proper MDM resolution is 30 × 30. The obtained MDMs of the correct DMS responses and shuffle-corrected correlograms are shown in Figure 8. As seen in Figure 8a, the TRs in some MDMs are well formed and correspond to lower-cost function values. For example, the pair input-output combinations (1, 1), (1, 2), and (1, 3) for output neuron 1 (CA1 region) and input neurons 1 to 3 (CA3 region) exhibit clear trigger regions and low Ising energy (less than −1.5), which indicate strong connectivity between these input-output neuron pairs. The pairs from (1, 4) to (1, 8) exhibit blurred MDMs and high Ising energy (more than −1), which indicate weak or no functional connectivity between these input-output neuron pairs. This finding is confirmed by the shuffle-corrected correlograms shown in Figure 8b. Generally the results from the correlograms match the MDM results in terms of functional connectivity, but some differences are seen for weakly connected pairs, such as (1, 6), (3, 6), (4, 6), (5, 6), (4, 8), and (6, 8). Although the Ising energy of these pairs is around −1, indicating that they are weakly linked, only some of the correlograms show a small peak, such as (5, 6), (4, 8), (6, 8). Since the functional connectivity map includes only strongly connected pairs, these weakly linked pairs are pruned out because they do not significantly contribute to the prediction performances.
Figure 8:
(a) The MDMs estimated from NMN using the human hippocampus training data for the correct DMS responses (b) The shuffle-corrected correlograms of the human hippocampus training data for the correct DMS responses.
The MIMO-NMN analysis results for correct and incorrect DMS responses are presented in Figures 9 and 10, respectively. Figure 9a and 10a show the functional connectivity maps between CA3 and CA1 neurons. The CA3 neuron is connected to the CA1 neuron when the corresponding Ising cost function value is less than −1.5. Figures 9b and 10b show the details of output spiking probability predictions for output neuron 2, and the MIMO-NMN model could provide precise spike timing predictions. The corresponding ROC curve indicates good prediction performance: the TPR reaches 0.7 and 0.8 for correct and incorrect DMS responses, while the FPR is only at 0.05. The ROC curves for all output neurons are shown in Figures 9c and 10c, which show that the prediction performances are very close for fully and functionally connected MIMO models, despite some minor differences for output neurons 6 to 8. It should be noted that for output neurons 4 and 5, since no input neurons are functionally connected to them, their ROC performances are also very low.
Figure 9:
(a) The functional connectivity map of the CA3 to CA1 neurons for the correct DMS responses. (b) Illustrative prediction of the firing probability of CA1 neuron 2. (c) ROC plots of the eight output (CA1) neurons. All results are from the test (out-of-sample) data set.
Figure 10:
Model predictions from the MIMO model for the incorrect DMS responses data. (a) The functional connectivity map of the CA3 to CA1 neurons. (b) Illustrative prediction of the firing probability of CA1 neuron 2. (c) ROC plots of the eight output (CA1) neurons. All results are from the test (out-of-sample) data set.
The functional connectivity maps in Figures 9a and 10a are validated by comparing the prediction performance of the respective functionally connected model with its fully connected counterpart. In addition, from Figures 9a and 10a, we can further tell there is no difference in the functional connectivity between correct and incorrect DMS responses.
7. Discussion
To develop neuroprostheses that can restore computational functions of the impaired regions, multi-input, multi-output (MIMO) nonlinear dynamic models are required to provide predictive capabilities from spike train data. Much research has been devoted to developing methods that can model neural systems, such as the Volterra-Wiener model and its variants, generalized linear modeling (GLM) methods, and linear-nonlinear Cascade (LNC) models. These three models usually consist of a set of linear filters, a nonlinear transformation function, and a spike generation process (Bernoulli or Poisson process), as summarized in Meyer et al. (2017). For estimation of the model parameters, least square estimation (LSE) and maximum likelihood estimation (MLE) are commonly used. The LSE is not optimal when the system output is binary spike train data since the errors would not follow gaussian distribution. The MLE may also suffer from estimation biases because of the imbalanced class problem (King & Zeng, 2001), as described in section 2. The imbalanced class problem could be exacerbated when only a limited number of data are available. In addition to estimation biases, MIMO models are prone to overfitting problems because the number of parameters grows dramatically with the number of inputs, number of linear filters, and order of nonlinearity, as shown in equation 2.11. Although collecting neural data with long periods would reduce the estimation and overfitting problems, the multi-neuronal activities recorded in the human brain are usually very short due to government regulations and patients’ health concerns. Therefore, we emphasize that the data collected from humans are more challenging to analyze than those of animals.
In order to achieve better estimation results and reduce overfitting problems for short data records, we proposed a novel MIMO-NMN approach. The NMN and MIMO-NMN employ the Ising cost function with MDM that help to overcome the imbalanced class problem. We have used the LNB model to generate synthetic data to demonstrate these advantages of the NMN approach over the NM method and the GLM method under different noise levels, as shown in Figures 6 and 7.
We notice that the NMN approach provides better estimations of the linear filters in the system, comparing the NMs in Figures 3 and 4 with the two filters in Figure 2. The results indicate that the LSE used by the NM method is not optimal and suffers from biases caused by nongaussian error distribution. In addition, the spiking probabilities of GLM in Figure 6a are much lower than in the NMN and NM methods when the output is a binary spike train. This phenomenon is probably caused by the estimation biases of GLM since the spiking probability p(n) is underestimated with the imbalanced class problem (King & Zeng, 2001). (See the descriptions in section 2).
We found that the NMN approach has several useful aspects. First, NMN emphasizes the separation between the spiking events (ones) and non-spiking events (zeros) rather than directly maximizing the prediction performance. Second, NMN is robust to output noise in the form of spurious spikes, generated by other unobserved inputs to the neuron. Third, MDM helps to compress the redundant zeros (non-spiking events) and augment ones (spiking events) using grid graph properties. Finally, unlike the conventional log loss or cross-entropy function, the Ising cost function is effective for highly imbalanced numbers of spikes and zeros and short data records.
In practice, we found that traditional PDM/NM and GLM methods are quite sensitive to the choice of hyperparameters, such as the number of Laguerre basis functions L, the critical parameter α that controls the declining rate of basis function, the order of nonlinearity Q, and the regularization strength parameter λ. Few other studies have explicitly stated their approaches of selecting these hyperparameters, including statistical test (Zanos et al., 2008), grid search (Song et al., 2013), Akaike’s information criterion (Truccolo et al., 2004), and Bayesian information criterion (BIC; Song et al., 2013; Geng & Marmarelis, 2017). However, these approaches are not computationally scalable for MIMO models. Considering a MIMO system with K outputs that can be decomposed of a set of K MISO models, we need to evaluate all the combinations of hyperparameters, K × NL × Nα × NQ × Nλ, which is computationally infeasible. The MIMO-NMN relieves this problem of searching hyperparameters. We found that in practice, the NMN approach is not sensitive to the number of basis function L(a typical choice of L would range from three to seven) because the NMN is capable of optimizing the parameter α to find the optimal linear filters (neuronal modes). Similar findings are also reported from the precursor model LVN (Geng et al., 2017). Since we use MDM to represent system nonlinearity, searching the nonlinear order is also avoided. For the NMN approach, the resolution of MDM should be selected based on model performance, as shown in Figure 5.
The concept of MDM is an extension of multi-input threshold in the traditional NM method by replacing the hard trigger (generates only zero or one) with spiking probability. MDM also shares similar concepts with previous histogram-based methods in the LNP and PDM models (Simoncelli et al., 2004; Marmarelis et al., 2014). However, the use of one-dimensional histograms assumes the independence of the outputs of the linear filters, which is not necessarily true. Due to the limited human hippocampus data, we restrict the MDM to be two-dimensional in this letter. The MDM can be extended to be higher dimensional (3 or above) if more data are available. The MDM and its associated Ising cost function (after the training process) could serve an indicator of how strongly the input and output are functionally connected. Based on this observation, we propose to use the MIMO-NMN approach for modeling the encoding dynamics and functional connectivity of neuronal ensembles with spike train data. We applied the MIMO-NMN method to multineuronal spike train data recorded intraoperatively in the CA3 and CA1 regions of the hippocampus of an epileptic patient performing a delayed-match-to-sample (DMS) task. The estimated MDMs and the values of Ising cost function reveal the functional connectivity of output (CA1) neurons with input (CA3) neurons. The resulting functional connectivity map between CA3 and CA1 neurons for correct and incorrect DMS responses is shown in Figures 9a and 10a, respectively. These functional connectivity maps share similar results, which are obtained from the traditional shuffle-corrected correlogram method, as shown in Figure 8. However, it should be noted that cross-correlations can sometimes suggest spurious relationships as a result of autocorrelation (Dean & Dunsmuir, 2006). Comparing the ROC curves of the functionally connected model with its fully connected counterpart in Figures 9 and 10, we can conclude that removing the connections between those neuronal pairs that are not functionally connected would not affect the overall predictive performance. The ROC curves in Figures 9 and 10 also indicate good prediction performance of the MIMO-NMN model.
Although MIMO-NMN is a promising approach, there are several limitations regarding our study, and future work is required to validate MIMO-NMN. First, we have presented only the initial results of a single patient using the MIMO-NMN model. In the future, more data from human hippocampus need to be analyzed, as well as data from other neural ensembles, such as the prefrontal cortex. Second, exploration is necessary regarding how many data are required for different methods with different imbalanced levels. To achieve this goal, comprehensive studies and comparisons need to be done with Volterra-Wiener, GLM, and LNC models using publicly available data from both animals and humans. Third, the physiological interpretations of the NMN need to be further investigated, such as the elliptical shapes of trigger regions, as shown in Figure 10a, and the correspondence of NMs and neural oscillations.
Acknowledgments
This work was supported by NIH-NIBIB grant P41-EB001978 and DARPA contract N66601-09-C-2081 to the Biomedical Simulations Resource at the University of Southern California. We thank the anonymous reviewers for the constructive comments and suggestions that greatly contributed to improving this letter.
Appendix: Construction of MDM
An illustration of constructing the MDM is shown in Figure 11 (we take the dimension size H = 2 as an example). Let u1 and u2 be the outputs of the two NMs. We define NM outputs that cause output y to be positive as spiking points and that cause output y to be zero as non-spiking points. The scatter plot of spiking and non-spiking points is shown in Figure 11b. The scatter plot is divided by Ngd × Ngd pixels, and the counts of spiking points and non-spiking points falling in the pixel [s1(i), s2(j)] are denoted as Np[s1(i), s2(j)] and Nz[s1(i), s2(j)], respectively.
Figure 11:
Illustration of MDM. (a) The outputs of NMs u1(n) and u2(n). The red points represent the spiking events. The blue points represent the non-spiking events. (b) The scatter plot of the spiking events and the non-spiking events. (c) The constructed MDM after calculating the firing ratio of each pixel (Geng et al., 2018).
The output of the NMN follows Bayes’ theorem:
| (A.1) |
The likelihood and prior can be approximated by
| (A.2) |
According to Bayes’ theorem:
| (A.3) |
Similarly:
| (A.4) |
Thus:
| (A.5) |
The spiking probability of each pixel in the MDM is
| (A.6) |
Therefore, the function of MDM is defined as
| (A.7) |
We use a “heat map” in Figure 11c to represent the MDM. The red areas correspond to high spiking probability, which is termed the trigger region (TR). The blue areas correspond to low spiking probability, which is termed the zero region (ZR). The resolution of MDM, which is determined by Ngd, should be properly selected during the training processes (see an example in section 5).
Contributor Information
Kunling Geng, Department of Biomedical Engineering and Biomedical Simulations Resource Center, University of Southern California, Los Angeles, CA, 90089, U.S.A..
Dae C. Shin, Department of Biomedical Engineering and Biomedical Simulations Resource Center, University of Southern California, Los Angeles, CA, 90089, U.S.A.
Dong Song, Department of Biomedical Engineering and Biomedical Simulations Resource Center, University of Southern California, Los Angeles, CA, 90089, U.S.A..
Robert E. Hampson, Department of Physiology and Pharmacology, Wake Forest School of Medicine, Winston-Salem, NC, 27157, U.S.A.
Samuel A. Deadwyler, Department of Physiology and Pharmacology, Wake Forest School of Medicine, Winston-Salem, NC, 27157, U.S.A.
Theodore W. Berger, Department of Biomedical Engineering and Biomedical Simulations Resource Center, University of Southern California, Los Angeles, CA, 90089, U.S.A.
Vasilis Z. Marmarelis, Department of Biomedical Engineering and Biomedical Simulations Resource Center, University of Southern California, Los Angeles, CA, 90089, U.S.A.
References
- Aertsen AM, Gerstein GL, Habib MK, & Palm G. (1989). Dynamics of neuronal firing correlation: Modulation of “effective connectivity.” Journal of Neurophysiology, 61(5), 900–917. [DOI] [PubMed] [Google Scholar]
- Aljadeff J, Lansdell BJ, Fairhall AL, & Kleinfeld D. (2016). Analysis of neuronal spike trains, deconstructed. Neuron, 91(2), 221–259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benjamin AS, Fernandes HL, Tomlinson T, Ramkumar P, VerSteeg C, Chowdhury RH, . . . Kording KP (2018). Modern machine learning as a benchmark for fitting neural responses. Frontiers in Computational Neuroscience, 12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berger TW, Baudry M, Brinton RD, Liaw JS, Marmarelis VZ, Park AY, & Tanguay AR (2001). Brain-implantable biomimetic electronics as the next era in neural prosthetics. Proceedings of the IEEE, 89(7), 993–1012. [Google Scholar]
- Berger TW, Hampson RE, Song D, Goonawardena A, Marmarelis VZ, & Deadwyler SA (2011). A cortical neural prosthesis for restoring and enhancing memory. Journal of Neural Engineering, 8(4), 046017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berger TW, Song D, Chan RH, & Marmarelis VZ (2010). The neurobiological basis of cognition: Identification by multi-input, multioutput nonlinear dynamic modeling. Proceedings of the IEEE, 98(3), 356–374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berger TW, Song D, Chan RH, Marmarelis VZ, LaCoss J, Wills J, . . . Granacki JJ (2012). A hippocampal cognitive prosthesis: Multi-input, multioutput nonlinear modeling and VLSI implementation. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 20(2), 198–211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bialek W, & van Steveninck RR (2005). Features and dimensions: Motion estimation in fly vision. arXiv:q-bio/0505003. [Google Scholar]
- Brody CD (1999). Correlations without synchrony. NeuralComputation, 11(7), 1537–1551. [DOI] [PubMed] [Google Scholar]
- Chawla NV, Japkowicz N, & Kotcz A. (2004). Special issue on learning from imbalanced data sets. ACM SIGKDD Explorations Newsletter, 6(1), 1–6. [Google Scholar]
- Chichilnisky EJ (2001). A simple white noise analysis of neuronal light responses. Network: Computation in Neural Systems, 12(2), 199–213. [PubMed] [Google Scholar]
- Dean RT, & Dunsmuir WT (2016). Dangers and uses of cross-correlation in analyzing time series in perception, performance, movement, and neuroscience: The importance of constructing transfer function autoregressive models. Behavior Research Methods, 48(2), 783–802. [DOI] [PubMed] [Google Scholar]
- French AS, & Marmarelis VZ (1995). Nonlinear neuronal mode analysis of action potential encoding in the cockroach tactile spine neuron. Biological Cybernetics, 73(5), 425–430. [DOI] [PubMed] [Google Scholar]
- Galar M, Fernandez A, Barrenechea E, Bustince H, & Herrera F. (2012). Areview on ensembles for the class imbalance problem: Bagging-, boosting-, and hybridbased approaches. IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews), 42(4), 463–484. [Google Scholar]
- Geng K, & Marmarelis VZ (2015). Pattern recognition of Hodgkin-Huxley equations by auto-regressive Laguerre Volterra network. BMC Neuroscience, 16(1), P156. [Google Scholar]
- Geng K, & Marmarelis VZ (2017). Methodology of recurrent Laguerre–Volterra network for modeling nonlinear dynamic systems. IEEE Transactions on Neural Networks and Learning Systems, 28(9), 2196–2208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geng K, Shin DC, Song D, Hampson RE, Deadwyler SA, Berger TW, & Marmarelis VZ (2018). Mechanism-based and input-output modeling of the key neuronal connections and signal transformations in the CA3-CA1 regions of the hippocampus. Neural Computation, 30(1), 149–183. [DOI] [PubMed] [Google Scholar]
- Gerwinn S, Bethge M, Macke JH, & Seeger M. (2008). Bayesian inference for spiking neuron models with a sparsity prior. In Platt JC, Koller D, Singer Y, & Roweis ST (Eds.), Advances in neural information processing systems, 20 (pp. 529–536). Cambridge, MA: MIT Press. [Google Scholar]
- Gerwinn S, Macke JH, & Bethge M. (2010). Bayesian inference for generalized linear models for spiking neurons. Frontiers in Computational Neuroscience, 4, 12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hampson RE, Song D, Robinson BS, Fetterhoff D, Dakos AS, Roeder BM, . . . Laxton AW (2018). Developing a hippocampal neural prosthetic to facilitate human memory encoding and recall. Journal of Neural Engineering, 15(3), 036014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He H, Bai Y, Garcia EA, & Li S. (2008). ADASYN: Adaptive synthetic sampling approach for imbalanced learning. In Proceedings of the IEEE International Joint Conference on Neural Networks (pp. 1322–1328). Piscataway, NJ: IEEE. [Google Scholar]
- Igarashi KM, Lu L, Colgin LL, Moser MB, & Moser EI (2014). Coordination of entorhinal-hippocampal ensemble activity during associative learning. Nature, 510(7503), 143. [DOI] [PubMed] [Google Scholar]
- Ising E. (1925). Beitrag zur theorie des ferromagnetismus. Zeitschrift für Physik, 31(1), 253–258. [Google Scholar]
- Kang Y, Escudero J, Shin D, Ifeachor E, & Marmarelis V. (2015). Principal dynamic mode analysis of EEG data for assisting the diagnosis of Alzheimer’s disease. IEEE Journal of Translational Engineering in Health and Medicine, 3, 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- King G, & Zeng L. (2001). Logistic regression in rare events data. Political Analysis, 9(2), 137–163. [Google Scholar]
- Kubat M, & Matwin S. (1997). Addressing the curse of imbalanced training sets: One-sided selection. In Proceedings of the 14th International Conference on Machine Learning (pp. 179–186). San Mateo, CA: Morgan Kaufmann. [Google Scholar]
- López V, Fernández A, García S, Palade V, & Herrera F. (2013). An insight into classification with imbalanced data: Empirical results and current trends on using data intrinsic characteristics. Information Sciences, 250, 113–141. [Google Scholar]
- Marmarelis PZ, & Marmarelis VZ (1978). Analysis of physiological systems: The white-noise approach. New York: Plenum Press. [Google Scholar]
- Marmarelis VZ (2004). Nonlinear dynamic modeling of physiological systems. Hoboken, NJ: Wiley. [Google Scholar]
- Marmarelis VZ, & Orme ME (1993). Modeling of neural systems by use of neuronal modes. IEEE Transactions on Biomedical Engineering, 40(11), 1149–1158. [DOI] [PubMed] [Google Scholar]
- Marmarelis VZ, Shin DC, Song D, Hampson RE, Deadwyler SA, & Berger TW (2013). Nonlinear modeling of dynamic interactions within neuronal ensembles using principal dynamic modes. Journal of Computational Neuroscience, 34(1), 73–87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marmarelis VZ, Shin DC, Song D, Hampson RE, Deadwyler SA, & Berger TW (2014). On parsing the neural code in the prefrontal cortex of primates using principal dynamic modes. Journal of Computational Neuroscience, 36(3), 321–337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McFarland JM, Cui Y, & Butts DA (2013). Inferring nonlinear neuronal computation based on physiologically plausible inputs. PLoS Computational Biology, 9(7), e1003143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer AF, Williamson RS, Linden JF, & Sahani M. (2017). Models of neuronal stimulus-response functions: elaboration, estimation, and evaluation. Frontiers in Systems Neuroscience, 10, 109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitsis GD, French AS, Höger U, Courellis S, & Marmarelis VZ (2007). Principal dynamic mode analysis of action potential firing in a spider mechanoreceptor. Biological Cybernetics, 96(1), 113–127. [DOI] [PubMed] [Google Scholar]
- Okatan M, Wilson MA, & Brown EN (2005). Analyzing functional connectivity using a network likelihood model of ensemble neural spiking activity. Neural Computation, 17(9), 1927–1961. [DOI] [PubMed] [Google Scholar]
- Paninski L. (2004). Maximum likelihood estimation of cascade point-process neural encoding models. Network: Computation in Neural Systems, 15(4), 243–262. [PubMed] [Google Scholar]
- Perkel DH, Gerstein GL, & Moore GP (1967). Neuronal spike trains and stochastic point processes: II. Simultaneous spike trains. Biophysical Journal, 7(4), 419–440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pillow JW, & Simoncelli EP (2006). Dimensionality reduction in neural models: An information-theoretic generalization of spike-triggered average and covariance analysis. Journal of Vision, 6(4), 414–428. [DOI] [PubMed] [Google Scholar]
- Prenger R, Wu MCK, David SV, & Gallant JL (2004). Nonlinear V1 responses to natural scenes revealed by neural network analysis. Neural Networks, 17(5–6), 663–679. [DOI] [PubMed] [Google Scholar]
- Saggar M, Meriçli T, Andoni S, & Miikkulainen R. (2007, August). System identification for the Hodgkin-Huxley model using artificial neural networks. In Proceedings of the International Joint Conference on Neural Networks (pp. 2239–2244). Piscataway, NJ: IEEE. [Google Scholar]
- Sandler RA, & Marmarelis VZ (2015). Understanding spike-triggered covariance using Wiener theory for receptive field identification. Journal of Vision, 15(9), 16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sandler RA, Geng K, Song D, Hampson RE, Witcher MR, Deadwyler SA, . . . Marmarelis VZ (2018). Designing patient-specific optimal neurostimulation patterns for seizure suppression. Neural Computation, 30(5), 1180–1208. [DOI] [PubMed] [Google Scholar]
- Sandler RA, Song D, Hampson RE, Deadwyler SA, Berger TW, & Marmarelis VZ (2015a). Model-based asessment of an in-vivo predictive relationship from CA1 to CA3 in the rodent hippocampus. Journal of Computational Neuroscience, 38(1), 89–103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sandler RA, Song D, Hampson RE, Deadwyler SA, Berger TW, & Marmarelis VZ (2015b). Hippocampal closed-loop modeling and implications for seizure stimulation design. Journal of Neural Engineering, 12(5), 056017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartz O, Pillow JW, Rust NC, & Simoncelli EP (2006). Spike-triggered neural characterization. Journal of Vision, 6(4). [DOI] [PubMed] [Google Scholar]
- Sharpee T, Rust NC, & Bialek W. (2004). Analyzing neural responses to natural signals: Maximally informative dimensions. Neural Computation, 16(2), 223–250. [DOI] [PubMed] [Google Scholar]
- Simoncelli EP, Paninski L, Pillow J, & Schwartz O. (2004). Characterization of neural responses with stochastic stimuli. Cognitive Neurosciences, 327–338. [Google Scholar]
- Song D, Chan RH, Marmarelis VZ, Hampson RE, Deadwyler SA, & Berger TW (2007). Nonlinear dynamic modeling of spike train transformations for hippocampal-cortical prostheses. IEEE Transactions on Biomedical Engineering, 54(6), 1053–1066. [DOI] [PubMed] [Google Scholar]
- Song D, Chan RH, Marmarelis VZ, Hampson RE, Deadwyler SA, & Berger TW (2009). Nonlinear modeling of neural population dynamics for hippocampal prostheses. Neural Networks, 22(9), 1340–1351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song D, Chan RH, Robinson BS, Marmarelis VZ, Opris I, Hampson RE, . . . Berger TW (2015). Identification of functional synaptic plasticity from spiking activities using nonlinear dynamical modeling. Journal of Neuroscience Methods, 244, 123–135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song D, Wang H, Tu CY, Marmarelis VZ, Hampson RE, Deadwyler SA, & Berger TW (2013). Identification of sparse neural functional connectivity using penalized likelihood estimation and basis functions. Journal of Computational Neuroscience, 35(3), 335–357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stevenson IH, Rebesco JM, Hatsopoulos NG, Haga Z, Miller LE, & Kording KP (2009). Bayesian inference of functional connectivity and network structure from spikes. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 17(3), 203–213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stevenson IH, Rebesco JM, Miller LE, & Körding KP (2008). Inferring functional connections between neurons. Current Opinion in Neurobiology, 18(6), 582–588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Theis L, Chagas AM, Arnstein D, Schwarz C, & Bethge M. (2013). Beyond GLMs: A generative mixture modeling approach to neural system identification. PLoS Computational Biology, 9(11), e1003356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Truccolo W, Eden UT, Fellows MR, Donoghue JP, & Brown EN (2005). A point process framework for relating neural spiking activity to spiking history, neural ensemble, and extrinsic covariate effects. Journal of Neurophysiology, 93(2), 1074–1089. [DOI] [PubMed] [Google Scholar]
- Williamson RS, Sahani M, & Pillow JW (2015). The equivalence of information-theoretic and likelihood-based methods for neural dimensionality reduction. PLoS Computational Biology, 11(4), e1004141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu FY (1982). The Potts model. Reviews of Modern Physics, 54(1), 235. [Google Scholar]
- Zanos TP, Courellis SH, Berger TW, Hampson RE, Deadwyler SA, & Marmarelis VZ (2008). Nonlinear modeling of causal interrelationships in neuronal ensembles. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 16(4), 336–352. [DOI] [PMC free article] [PubMed] [Google Scholar]