مشتق

| اصطلاح | term |
|---|---|
| مشتق/اشتقاقی مشتقات اشتقاق حسابان لمحاتی مماسی مائل |
derivative derivatives derivation calculus instantaneous tangent slope |
ریاضیات کی شاخ احصا میں مشتق ناپ ہے کہ دالہ کس طرح تبدیل ہوتی ہے حب اس کا ادخال تبدیل ہو۔ عامی زبان میں، مشتق سے مراد یہ ہے کہ کوئی قدر کسی نقطہ پر کتنا تبدیل ہو رہی ہے؛ مثلاً کسی گاڑی کے مقام کا وقت کے حوالے سے مشتق گاڑی کا لمحاتی سمتار ہے جس کے مطابق گاڑی سفر کر رہی ہے۔ بالعکس، سمتار کا وقت پر متکامل گاڑی کے مقام میں تبدیلی بتاتا ہے۔
فنکشن کا چنے ہوئے ادخال نقطہ پر مشتق اس نقطہ کے آس پاس فنکشن کے بہترین لکیری تقرب کی توضیح کرتا ہے۔ ایک متغیر کی حقیقی قدر فنکشن کے لیے، کسی نقطہ پر فنکشن کا مشتق اس دالہ گراف میں اس نقطہ پر مماسی کے مائل کے برابر ہوتا ہے۔ زیادہ بُعد میں، کسی نقطہ پر فنکشن کا مشتق لکیری استحالہ ہے جسے لکیرانا کہتے ہیں۔ اس سے ملتا جلتا تصور دالہ کا تفرقی کا ہے۔
مشتق کے ڈھونڈنے کے عمل کو تفرق کہتے ہیں۔ حسابان کا بنیادی مسئلہ اثباتی بتاتا ہے کہ تفرق کا عمل تکامل کا مقلوب ہے۔

تفرق اور مشتق
[ترمیم]تفرق، ادخال x میں تبدیلی سے اخراج y میں رونما ہونے والی تبدیلی کی شرح نکالنے کا طریقہ ہے۔ اس تبدیلی کی شرح کو x کی رو سے y کا مشتق کہا جاتا ہے۔ متغیر y کے x پر انحصار کو ریاضیاتی طور پر کہا جاتا ہے کہ y دالہ ہے x کا۔ اس دالاتی رشتہ کو عموماً y = ƒ(x) کی علامت سے لکھتے ہیں۔ اگر x اور y حقیقی ہوں اور y کو x کے برخلاف بطور دالہ کے مخط نکشہ کیا جائے، تو مشتق گراف کے ہر نقطہ پر گراف کے مائل کو ناپتا ہے۔
سب سے سادہ ماجرا یہ ہے جب y لکیری فنکشن ہو x کا، جس کا مطلب ہے کہ y برخلاف x کا گراف خطی لکیر ہے۔ اس ماجرے میں، y = ƒ(x) = m x + c ، جہاں m اور c حقیقی اعداد ہیں اور مائل m اس طرح دی جاتی ہے
جہاں علامت Δ (یونانی حرف ڈیلٹا) مختصر ہے "میں تبدیلی (change in)" کے لیے۔ یہ کلیہ سچ ہے کیونکہ
- y + Δy = ƒ(x+ Δx) = m (x + Δx) + c = m x + c + m Δx = y + mΔx
اس سے پتہ چلتا ہے کہ Δy = m Δx
یہ ہمیں خطی لکیر کی مائل کی ٹھیک قدر بتا دیتا ہے۔ اگر تفاعل ƒ لکیری نہ ہو (یعنی اس کا گراف خطی لکیر نہ ہو)، تو "y میں تبدیلی" تقسیم "x میں تبدیلی" مختلف ہو گی x کی مختلف قدروں کے لیے؛ تفرق ہمیں اس "شرحِ تبدیلی" کی ٹھیک قدر معلوم کرنے کا طریقہ بتاتا ہے،x کی کسی بھی قدر کے لیے۔

| اصطلاح | term |
|---|---|
|
قسیم |
quotient |

یہ خیال، جس کو اشکال 1-3 میں دکھایا گیا ہے، یہ ہے کہ شرح کو بطور کی حدی قدر شمارندی کیا جائے جب Δx لامتنہائی چھوٹا ہوتا جائے۔ لائیبنز کی علامت میں x میں لامتنہائتی تبدیلی کو dx لکھا جاتا ہے اور y کا مشتق x کی رُو سے، کو یوں لکھا جاتا ہے
جو ان دو لامتناہیتی اقدار کے تناسب کا خیال ذہن میں پیدا کرتا ہے۔ اس اظہار کو یوں پڑھا جاتا ہے، y کا مشتق x کی رُو سے یا dy سے dx یا dy اوپر dx ۔
تصویر سے ظاہر ہے کہ نقطہ P پر مماسی لکیر کی مائل ہے، جبکہ اصل تفاعل f کا نقطہ P سے آگے "چڑھاؤ-اوپر-بھاگ" (rise-over-run) ہے۔
فرق قسیم سے تعریف
[ترمیم]چلو y=f(x) اور جہاں ƒ حقیقی قدر والی تفاعل ہو۔ کلاسیکی ہندسہ میں نقطہ a پر مماسی لکیر وہ ہوتی تھی جو نقطہ (a, ƒ(a)) سے گذرے مگر تفاعل کے گراف کو کسی اور نقطہ پر قطع نہ کرے۔ اس صورت میں y کا مشتق x کی رُو سے نقطہ x=a پر اس مماسی لکیر کے مائل کے برابر ہے۔ اس مماسی کی مائل ایسی لکیر جو نقطہ (a, ƒ(a)) اور قریبی نقطہ (a + h, ƒ(a + h)) سے گذر رہی ہو کے مائل سے بڑی قریب ہو گی۔ ایسی لکیروں کو "لکیرِ قاطع" کہتے ہیں۔ اگر h صفر کے قریب ہو تو لکیر قاطع کا مائل بڑا قریب ہو گا مماسی کے مائل کے اور اگر h کی مطلق قدر جتنی کم ہو تقرب اتنا ہی بہتر ہو گا۔ لکیرِ قاطع کا مائل m ان نقاط پر جہاں یہ تفاعل f کو قطع کرتے ہیں کی "y اقدار کے فرق" کو "x اقدار کے فرق" سے تقسیم کرنے سے ملتا ہے:
یہ اظہاریہ نیوٹن کا فرق قسیم ہے۔ مشتق اس فرق قسیم کی وہ قدر ہے جب لکیرِ قاطع قریب تر ہوتی جاتی ہے مماسی لکیر کے۔ رسمی طور پر فنکشن f کا a پر مشتق اس فرق قسیم کی حد ہے
جب h صفر کے قریب تر ہوتا جائے، اگر یہ حد وجود رکھتی ہو۔ اگر اس حد کا وجود ہو تو فنکشن f نقطہ a پر تفرقاً ہے۔ یہاں ƒ′ (a) مشتق کی بہت سی علامتوں میں سے ایک ہے۔
مساوانہ، مشتق اس خاصہ کی تسکین کرتا ہے
جس کی وجدانی تفسیر (شکل 1) ہے کہ فنکشن f کی مماسی لکیر نقطہ a پر f کا بہترین لکیری تقرب ہے
(چھوٹے h کے لیے)۔ دوسری طاقمات میں اس تفسیر کو جامع کرنا آسان ترین ہے۔
اگر h کی جگہ 0 لگایا جائے تو صفر سے تقسیم ہو جائے، اس لیے لکیر کی مائل سیدھی طرح معلوم کرنا ممکن نہیں ہوتا۔ اس کی بجائے فرق قسیم کو h کی فنکشن کے طور پر Q(h) تعریف کیا جاتا ہے:
نقاط (a, ƒ(a)) اور (a + h, ƒ(a + h)) کے درمیان لکیرِقاطع کا مائل Q(h) ہے۔ اگر فنکشن f استمری ہو، یعنی اس کا گراف ثابت منحنی ہو بغیر وقفوں کے، تو نقطہ h = 0 سے پرے Q بھی استمری ہے۔ اگر حد وجود رکھتی ہو، مطلب کہ ایسا طریقہ ہو کہ Q(0) کی ایسی قدر چنی جا سکے جو Q کو استمری فنکشن بنا دے، تو فنکشن f تفرقاً ہے نقطہ a پر اور اس کا مشتق نقطہ a پر Q(0) کے برابر ہے۔
ممارست میں، استمری Q(h) کا وجود نقطہ h = 0 پر دکھانے کے لیے، numerator کو اس طرح مڑورا جاتا ہے کہ h numerator اور denominator میں کٹ جائے۔
مثال
[ترمیم]مربعاتی فنکشن ƒ(x) = x2 نقطہ x = 3 پر تفرقاً ہے اور اس کا مشتق وہاں 6 ہے۔ اس نتیجہ کو یوں قائم کیا جاتا ہے:
اب مشتق حاصل کرنے کے لیے ہم جانے دیتے ہیں
اوپر کے اظہاریہ سے معلوم ہوتا ہے کہ قسیم 6 + h کے برابر ہے جب h غیر صفر ہو اور ناتعریف شدہ ہوتا ہے جب h صفر ہو۔ (یاد رہے کہ فرق قسیم کی تعریف کی رُو سے، فرق قسیم h کی صفر قدر کے لیے کبھی تعریف نہیں ہوتا)۔ البتہ صفر پر فرق قسیم کی قدر پوری کرنے کا قدرتی طریقہ ہے، جو یہاں 6 ہے۔ اس لیے مربعاتی فنکشن کے گراف پر نقطہ (3, 9) پر مائل کی قدر 6 ہے اور اس لیے x = 3 پر مشتق کی قدر ƒ '(3) = 6 ہے۔
جامعاتی طور پر، اسی طرح کی شمارندگی سے پتہ چلتا ہے کہ x = a پر مربعاتی تفاعل کا مشتق ƒ '(a) = 2a ہے۔
خیال رہے کہ مشتق کی اوپر تعریف (لکیرِ قاطع کی حد) کلاسیکی ہندسہ میں مماسی کی تعریف پر منحصر نہیں۔ خاص طور پر کسی نقطہ پر یوں معلوم ہونے والا مماسی تفاعل کو کسی جگہ قطع بھی کر سکتا ہے۔
استمری اور تفرقاً
[ترمیم]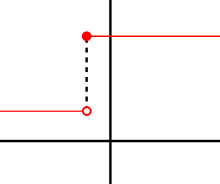
اگر y = ƒ(x) تفاعل a پر تفرقاً ہو، تو لازمی طور پر تفاعل a پر استمری ہو گی۔ مثال کے طور پر قدم دالہ (تصویر) جو نقطہ x=a سے پہلے صفر ہے اور x=a پر اور اس کے بعد 1، یہ تفاعل نقطہ x=a پر لاستمری ہے۔ اگر h منفی ہو تو a+h قدم کے نچلے حصے پر ہو گا اور a+h سے a تک جاتی لکیر قاطع بہت ڈھلونی ہو گی۔ دوسر طرف h اگر مثبت ہو تو a+h قدم کے اوپرلے حصے پر ہو گا اور a سے a+h جاتی لکیر قاطع کا مائل صفر ہو گی۔ نتیجتاً لکیر قاطع کسی یکساں مائل کی طرف نہیں جاتی، اس لیے قسیم کی حد موجود نہیں۔ اس لیے x=a پر اس تفاعل کا مشتق وجود نہیں رکھتا۔ اس کے باوجود اس نقطہ پر توزیع کا نظریہ استعمال کرتے ہوئے مشتق تعریف کیا جا سکتا ہے۔

البتہ اگر تفاعل کسی نقطہ پر استمری بھی ہو پھر بھی ممکن ہے کہ وہاں تفرقاً نہ ہو۔ مثال کے طور پر مطلق قدر تفاعل نقطہ x=0 پر استمری ہے، مگر وہاں تفرقاً نہیں۔ اگر h مثبت ہو تو 0 سے h تک لکیرِ قاطع کا مائل 1 ہے، جبکہ اگر h منفی ہو تو 0 سے h تک لکیرِ قاطع کا مائل -1 ہے۔ گرافی طور پر اسے نقطہ صفر پر نوک کے طور پر دیکھا جا سکتا ہے۔
مختصراً یہ کہ تفاعل کے مشتق کے وجود رکھنے کے لیے ضروری ہے کہ تفاعل استمری ہو، مگر استمری ہونا تفاعل کے تفرقاً ہونے کے لیے کافی نہیں۔
مشتق بطور تفاعل
[ترمیم]چلو f تفاعل ہو جس کا اپنی ساحہ میں ہر نقطہ a پر مشتق وجود رکھتا ہو۔ چونکہ ہر نقطہ a پر مشتق ہے، اس لیے ایک تفاعل ایسی ہے جو نقطہ a کو تفاعل کے مشتق میں بھیجتی ہے۔ اس تفاعل کو f′(x) لکھا جاتا ہے اور اسے مشتق فنکشن کہتے ہیں یا f کا مشتق۔
کبھی یوں بھی ہوتا ہے کہ کا مشتق ساحہ کے زیادہ تر نقاط، مگر تمام نہیں، پر وجود رکھتا ہے۔ ایسی تفاعل جو نقطہ a پر f کے مشتق f′(a) کے برابر ہو جب بھی مشتق وجود رکھتا ہو اور دیگر نقاط پر غیر تعریف شدہ ہو، کو بھی تفاعل کا مشتق کہتے ہیں۔ یہ f′ تفاعل ہوتی ہے مگر اس کا ساحہ f کے ساحہ سے چھوٹا ہوتا ہے۔
اس خیال کے استعمال سے، تفرق دالہات کا تفاعل بن جاتا ہے: تفرق ایک عالج ہے جس کا ساحہ ایسے تمام دالہات کا مجموعہ ہے جن کا مشتق ان کی ساحہات میں ہر نقطہ پر وجود رکھتا ہے اور اس کا حیطہ دالہات کا مجموعہ ہے۔ اگر اس عالج کو D کی علامت دی جائے، تو D(f) برابر ہے تفاعل f′(x) کے۔ چونکہ D(f) تفاعل ہے، اس لیے اسے نقطہ a پر جانچا جا سکتا ہے۔ مشتق کی تعریف کے مطابق D(ƒ)(a) = f′(a) ہو گا۔
مقابلے کے لیے، دوگنیاتی تفاعل ƒ(x) =2x کو دیکھو؛ تفاعل ƒ حقیقی قدر والی ہے اور حقیقی عدد کی تفاعل ہے، یعنی حقیقی عدد ادخال کرتی ہے اور حقیقی عدد اخراج کرتی ہے:
عالج D البتہ انفرادی اعداد کے لیے تعریفدہ نہیں، یہ صرف دالہات کے لیے تعریف ہے:
چونکہ D کا اخراج تفاعل ہے، D کے اخراج کو کسی نقطہ پر جانچا جا سکتا ہے۔ مثال کے طور پر، اگر D کو مربعاتی تفاعل پر اطلاق کیا جائے تو،
D کا اخراج دوگنیاتی تفاعل ہے،
جس کا نام ہم ƒ(x) رکھتے ہیں۔ اس اخراج تفاعل کو جانچا جا سکتا ہے، ƒ(1) = 2، ƒ(2) = 4 اور اسی طرح۔
| اصطلاح | term |
|---|---|
| مشتقات مرتب بالا | higher order derivatives |
مشتقاتِ بالا
[ترمیم]چلو f تفرقاً تفاعل ہو اور f′(x) اس کا مشتق۔ تفاعل f′(x) کا مشتق (اگر وجود رکھتا ہو) کو f′′(x) لکھا جاتا ہے اور اسے f کا دوسرا مشتق کہا جاتا ہے (f کا پہلا مشتق f′(x) ہے)۔ اسی طرح، مشتقِ دوم کا مشتق، اگر وجود رکھتا ہو، کو f′′′(x) لکھا جاتا ہے اور اسے f کا تیسرا مشتق کہا جاتا ہے۔ ان بتکرار مشتقات کو بالا مرتب مشتقات کہا جاوے ہے۔
کسی فنکشن f کا مشتق ہونا ضروری نہیں۔ بعینہ اگر f کا مشتق ہو بھی، تو ہو سکتا ہے اس کا دوسرا مشتق وجود نہ رکھتا ہو۔ مثال کے طور پر، چلو
ابتدائی حسابگری سے پتہ چلتا ہے کہ f تفرقاً ہے جس کا مشتق
f′(x) مطلق قدر فنکشن کا دوہرا ہے، جس کا صفر پر مشتق وجود نہیں رکھتا۔ اس طرھ کی مثالوں سے پتہ چلتا ہے کہ ہو سکتا ہے کہ کسی فنکشن کے k مشتق ہوں (کسی غیر منفی صحیح عدد k کے لیے) مگر (k+1)-واں مرتب مشتق نہ ہو۔ ایسی فنکشن جو مسلسل k مرتبہ تفرقاً ہو کو k-بار تفرقاً کہا جاتا ہے۔ اس کے علاوہ اگر k-واں مشتق استمری ہو تو تفاعل کو تفرقاً جماعت Ck کا رکن مانا جاتا ہے۔ (یہ k مرتبہ تفرقاً ہونے سے مظبوط تر شرط ہے۔) جس فنکشن کے لامتناہی مشتقاتِ بالا ہوں اسے لامتناہی تفرقاً یا ہموار کہا جاتا ہے۔
ھقیقی لکیر پر، ہر کثیر رقمی دالہ لامتناہی بار تفرقاً ہے۔ تفرق کے معیاری قواعد کی رُو سے، اگر درجہ n کا کثیر رقمی n بار تفرق کیا جاوے، تو یہ دائم دالہ بن جاتا ہے۔ اس کے تمام اگلے مشتق شناختی صفر ہیں۔ خاص طورانہ، یہ وجود رکھتے ہیں، اس لیے کثیر رقمی ہموار فنکشن ہیں۔
فنکشن f کے نقطہ x پر مشتق اس فنکشن کے نقطہ x کے آس پاس کثیر رقمی تقرب فراہم کرتے ہیں۔ مثالاً، اگر f دو بار تفرقاً ہو، تو
ان معنوں میں کہ
اگر f لامتناہی بار تفرقاً ہووے تو یہ اس فنکشن کے ٹیلر سلسلہ کی ابتدا ہے۔
تفرق کی علامات
[ترمیم]لائیبنیز کی علامت
[ترمیم]لائیبنیز کی متعارف کرائی علامات اولین میں سے ہیں۔ یہ اب بھی عام استعمال ہوتی ہے جب y = ƒ(x) کو آزاد اور تابع متغیر میں فنکشناتی نسبت کے طور پر سمجھا جائے۔ مشتقِ اول کو پھر اس علامات سے تعبیر کیا جاتا ہے
مشتقاتِ بالا کا اظہار اس علامات سے کیا جائے ہے
y = ƒ(x) کے n-ویں مشتق (x کی رو سے ) کے لیے۔ یہ مشتقی عالج کے متعدد اطلاق کی مختصر صورت ہے۔ مثلاً
لائیبنز کی علامت سے ہم نقطہ x = a پر y کے x کی رو سے مشتق کو دو مختلف طریق سے لکھ سکتے ہں:
لائیبنز کی خوبصورت علامت سے ہم تفرق کے متغیر کو denominator میں لکھ سکتے ہیں۔ یہ جزوی تفرق میں خاص طور پر مفید ہے۔ اس سے زنجیر قاعدہ کو یاد رکھنا بھی آسان رہتا ہے::
لاگرینج کی علامات
[ترمیم]ایک عام استعمال ہونے والی علامت لاگرینج کی ہے جو اولی نشان کا استعمال کرتا ہے، اس طرح فنکشن ƒ(x) کا مشتق ƒ′(x) لکھا جاتا ہے یا صرف ƒ′ ہی۔ اسی طرح دوسرا اور تیسرے مشتق کو
- اور
لکھا جاتا ہے۔ اس کے بعد عدد استعمال کیے جاتے ہیں، مثلاً
چوتھا مشتق ہو گا۔ جامع طور پر n-ویں مشتق کو ƒ (n) لکھا جائے گا۔
نیوٹن کی علامات
[ترمیم]نیوٹن کی علامت، جسے نقطہ علامت بھی کہتے ہیں، فنکشن کے نام کے اوپر نقطہ ڈال کر مشتق ظاہر کیا جاتا ہے۔ اگر y = ƒ(t) ہو، تو
- اور
علترتیب متغیر y کے پہلے اور دوسرے مشتق کو ظاہر کرتا ہے متغیر t کی رُو سے۔ یہ علامت عام طور پر وہیں استعمال ہوتی ہے جہاں آزاد متغیر وقت ہو اور طیبیعیات میں عام ملتی ہے جیسا کہ تفرقی مساوات میں۔
عائلر کی علامات
[ترمیم]عائلر کی علامت تفرقی عالج D استعمال کرتی ہے، جسے جب فنکشن f پر اطلاق کیا جائے تو پہلا مشتق Df ملتا ہے۔ دوسرے مشتق کو D2ƒ اور n-ویں مشتق کو Dnƒ لکھا جاتا ہے۔
اگر y = ƒ(x) تابع متغیر ہو، تو x کو ذیلی نص کے طور پر D سے نتھی کیا جاتا ہے یہ واضح کرنے کے لیے کہ آزاد متغیر x ہے۔ عائلر کی علامت پھر یوں لکھی جاتی ہے
- اور
اگرچہ ذیلی نص اکثر نہیں لگایا جاتا جب یہ واضح ہو کہ مراد x ہی ہے، جیسا کہ جب اظہاریہ میں صرف ایک ہی متغیر موجود ہو۔ عائلر کی علامت لکیری تفرقی مساوات میں مفید ثابت ہوتی ہے۔
مشتق کی شمارندگی
[ترمیم]فنکشن کا مشتق جیسے اوپر بیان ہوا، قسیم فرق کی تعریف اور اس کی حد سے شمارند کیا جا سکتا ہے۔ عملی طور پر جب کچھ سادہ فنکشنات کے مشتق معلوم ہوں، تو دوسری فنکشنات کے مشتق ان سے مشتق حاصل کرنے کے "قواعد" استعمال کرتے ہوئے ڈھونڈے جا سکتے ہیں۔
ابتدائی دالہات کے مشتق
[ترمیم]تقریباً سبھی مشتق آخرکار کچھ ابتدائی دلہات کے مشتق درکار کرتے ہیں۔ نیچے یکی متغیر کی کچھ فنکشنات اور ان کے مشتقات کی ایک نامکمل فہرست دی ہے:
- طاقت کے مشتقات: اگر
جہاں r کوئی حقیقی عدد ہے، تو
جب بھی یہ فنکشن تعریف شدہ ہو۔ مثلاً r=1/2 کے لیے
اور یہ فنکشن صرف غیر منفی x کے لیے تعریف ہے۔ جب r=0 ہو، تو مشتق کا دائم قاعدہ حاصل ہوتا ہے۔
مشتق ڈھونڈنے کے قواعد
[ترمیم]بہت دفعہ نیوٹن کے فرق قسیم کے حد کی پچیدہ حسابگری سے تفرقی قواعد کے استعمال سے بچا جا سکتا ہے۔ کچھ انتہائی ابتدائی قواعد ذیل ہیں:
- دائم قاعدہ: اگر
f(x)دائم ہو، تو
- تمام دالہات ƒ اور g اور حقیقی اعداد a اور b کے لیے۔
- تمام دالہات ƒ اور g کے لیے۔
- تمام دالہات ƒ اور g جہاںg ≠ 0
- زنجیر قاعدہ: اگر ، تو
مثال شمارندگی
[ترمیم]ذیل فنکشن کا مشتق
یہ ہے
یہاں دوسری اصطلاح "زنجیر قاعدہ" اور تیسری "ضرب قاعدہ" سے حاصل ہوئی۔ ابتدائی فنکشنات x2، x4،
sin(x)،
ln(x)
اور
exp(x) = ex
اور دائم 7 کے معلوم مشتق بھی استعمال ہوئے۔
سمتیہ قدر تفاعل کا مشتق
[ترمیم]کسی حقیقی متغیر کی سمتیہ قدر فنکشن y(t) حقیقی اعداد کو سمتیہ مکاںء Rn میں بھیجتی ہے۔ سمتیہ-قدر فنکشن کو اس کے متناسق فنکشن y1(t), y2(t), …, yn(t) میں بانٹا جا سکتا ہے، مطلب کہ y(t) = (y1(t), ..., yn(t)) ہو۔ چونکہ متناسق فنکشن حقیقی قدر ہیں اس لیے مشتق کی اوپر دی تعریف کا اطلاق ہو گا۔ فنکشن y(t) کا مشتق بھی سمتیہ ہو گا، جسے مماسی سمتیہ کہیں گے اور اس کے متناسق، سمتیہ کے متناسق کے مشتق ہوں گے۔ یعنی
برابراً
اگر حد وجود رکھتی ہو۔ numerator میں تفریق سمتیہ کی تفریق ہے۔ اگر y کا مشتق تمام کے لیے وجود رکھتا ہو، تو y′ ایک اور سمتیہ-قدر فنکشن ہے۔
اگر Rn میں e1, …, en معیاری بنیاد ہو، تو y(t) کو یوں y1(t)e1 + … + yn(t)en لکھا جا سکتا ہے۔ اگر ہم لکیری خاصیت فرض کریں، تو y(t) کا مشتق ضرور ہو گا
کیونکہ ہر بنیاد سمتیہ دائم ہے۔
یہ جامعیت خاصی مفید رہتی ہے، مثال کے طور پر اگر کسی زرّے کا وقت t پر مقام سمتیہ y(t) ہو؛ تو اس کا وقت t پر سمتار y′(t) ہو گا۔
E=mc2 اردو ویکیپیڈیا پر ریاضی مساوات کو بائیں سے دائیں LTR پڑھیٔے ریاضی علامات





























































