Graph Time-series Modeling in Deep Learning: A Survey

Learning informative representations of nodes remains one of the most important tasks in deep graph learning. The learned node embeddings can be used in many tasks [18, 34]. Earlier models leverage random walk [25, 34], while recent models advance node embedding performance with neural network layers that efficiently aggregate neighboring node information and model the non-linear inter-dependency between nodes to assist representation learning [41, 58, 77].

Given a graph \(G = (V, E)\) with a node set V and an edge set E, and features \(\boldsymbol {\mathrm{X}}\in \mathbb {R}^{N \times d}\) of \(N=|V|\) nodes and d dimensions, the goal of node embedding is to learn a hidden state \(\mathbf {h}_v \in \mathbb {R}^{d_h}\) of a selected dimension \(d_h\) for each node \(v \in V\). A generalized node embedding graph model takes the formwhere \(\theta\) denotes the GNN structure and parameters. The equation implies that the embedding of node v relies on both its input features and the embeddings of other nodes. In practice, the range of other nodes is limited to a neighborhood set of v, denoted by \(\Gamma (v)\), thus resulting in \(u \in \Gamma (v)\).

GNNs constitute the majority of recent graph-based deep learning models [81, 97]. We briefly introduce how graph structures are leveraged in some of the most successful GNN models.

Graph Convolutional Networks (GCN) operate directly on graph structures with graph convolutional layers, which is considered a counterpart of CNNs that operate on grid-structured data [41]. For each node in the graph, the GCN model aggregates information from other nodes based on their connection strength, i.e., nodes in proximity have more impact than distant nodes. A graph convolutional layer allows the aggregation of one-hop neighboring nodes. Multi-hop neighborhood aggregation can be achieved by stacking several graph convolutional layers. Essentially, GCN can be seen as a node embedding method and it was initially applied to a node classification task.

Graph Attention Networks (GAT) integrate the attention mechanism, which consists of self-attentional layers that learn pairwise relations between nodes based on node embeddings [77]. Although the standard GAT takes the graph connectivity information as input, GAT can assume a complete graph when such connectivity information is missing. Node embeddings are used to compute attention scores, which consequently serve as edge weights in the graph. This gives two-fold advantages. First, the attention scores offer a plausibly intuitive interpretation of mutual impacts between nodes. Second, the node embeddings and attention scores can be iteratively computed in turn, providing a self-contained and relatively simple model regarding parameter complexity. Furthermore, external graph structure knowledge, whenever it exists, can be utilized to select attention scores to compute. Similarly, the GAT model can be seen as a node embedding method that learns a hidden state for each node by incorporating their neighborhood information.

RNN models, as described in Equation (4)–Equation (8), can perform node message propagation by substituting the weight matrix multiplication with graph convolution or graph diffusion. Hence, the modified RNN models not only model the temporal dependency through its recursive nature but also capture the non-linear mutual impacts among nodes. In this category, we cover GCRN, DCRNN, and DGSL, all of which nest the GNN model within an RNN cell, as depicted in Figure 2.

GCRN [69] substitutes fully connected layers in LSTM with graph convolutional layers. Specifically, the weight matrix multiplication for all gates in the LSTM is replaced with GCN, resulting in an LSTM variant denoted as \(\text{LSTM}^\ast\),GCRN leverages the graph structure for training, which allows each node to efficiently aggregate neighborhood information, in contrast to a raw RNN (in this case, the LSTM model) that models the dependency between nodes by dense neural layers. The GCRN model takes a similar form to an LSTM model, therefore, the derived hidden state in Equation (46) is sensibly used in time-series forecasting tasks in the same way as how the hidden state is used in LSTM. See Section B.1 for detailed equations.

DCRNN [51] uses diffusion convolution to replace the weight matrix multiplication in a different RNN variant, the Gated Recurrent Units (GRU). The graph diffusion operator, denoted by \(g_\mathbf {\theta }(\cdot)\) with respect to parameters \(\mathbf {\theta }\) and an adjacency matrix \(\boldsymbol {\mathrm{A}}\), is defined aswhere \(\boldsymbol {\mathrm{D}}_O, \boldsymbol {\mathrm{D}}_I\) denotes the in-degree matrix and the out-degree matrix, respectively. The model utilizes the random walk matrix \(\boldsymbol {\mathrm{D}}_O^{-1} \boldsymbol {\mathrm{A}}\) and \(\boldsymbol {\mathrm{D}}_I^{-1} \boldsymbol {\mathrm{A}}^\mathsf {T}\) for information propagation. Regarding the temporal component, GRU is chosen instead of LSTM, which brings the benefit of lighter computing workloads due to the simpler structure of GRU model. DCRNN inspires many subsequent models, including DGSL [70], T-GCN [100], and GraphDF [9].

DGSL [70] can be seen as a DCRNN variant with a probabilistic graph, where the graph structure is learned from time-series data. Given time-series data \(X \in \mathbb {R}^{N \times T \times d}\), a graph \(\boldsymbol {\mathrm{A}}\in \left\lbrace 0, 1 \right\rbrace ^{N\times N}\) is parameterized and sampled by the following equations:where \(g_{ij}^1, g_{ij}^2 \sim \text{Gumbel}(0, 1)\) (Defined in Section C.5). A binary graph is constructed by sampling edges from distributions in Equation (15), which leverages the Gumbel reparameterization method [38], with s a selected constant parameter. The parameter \(\theta _{ij}\) for each node pair is learned from a link prediction method that takes node embeddings as input as in Equation (14). With the sampled graph, DGSL renders the DCRNN model for sequence-to-sequence training and forecasting. Since the graph in DGSL is parameterized with the time-series data, it optimizes trainable parameters for both time-series and graph learning simultaneously.

More recent methods construct graphs in various ways for tasks other than time-series forecasting. For instance, VGCRN [10] takes a probabilistic approach and builds a deep variational network for time-series anomaly detection. GANF [16] builds a graph-augmented flow model with a Bayesian network that models the causal relationships between time-series for time-series anomaly detection. Moreover, GRIN [13] targets time-series imputation with GNN and RNN.

Model Comparison. For graph modeling, GCRN uses GCN that operates on undirected graphs, while DCRNN and DGSL use graph diffusion, which has the advantage of modeling directed graphs. Further, GCRN and DCRNN require external graph structures, while DGSL takes a probabilistic approach and learns graph structures from node embeddings without using a pre-defined graph. A diagram of Graph RNN cell is shown in Figure 3, which highlights the distinctions and commonalities among the chosen models.

Another line of work models time-series through CNN instead of RNN.

STGCN [90] models the graph structure and temporal dependence individually with separate layers, instead of nesting graphs in the RNN structure. STGCN proposes a spatio-temporal convolutional block that consists of temporal-spatial-temporal layers. The temporal layer is built upon a 1D convolutional layer with gated linear units and requires less time complexity compared to RNN models. The spatial layer, however, is made of a GCN layer. Therefore, STGCN inspires a separate and individual view and usage of temporal and spatial dimensions.

Graph WaveNet [83] points out that the explicitly given graph structure may not be able to represent relations between nodes due to missing node connections. To mitigate the missing information and the ineffectiveness of the RNN component, Graph WaveNet develops an adaptive adjacency matrix and it also replaces RNN models with stacked dilated convolutional layers. With respect to the graph modeling, Graph WaveNet adapts the graph diffusion layer from DCRNN by adding a third term of an adaptive adjacency \(\boldsymbol {\mathrm{A}}_{adapt}\) to the diffusion matrix in Equation (13):where the adaptive matrix is learned through the embeddings \(\boldsymbol {\mathrm{H}}_{emb1}\) and \(\boldsymbol {\mathrm{H}}_{emb2}\), which are independent of the given graph structure. Both \(\boldsymbol {\mathrm{H}}_{emb1}\) and \(\boldsymbol {\mathrm{H}}_{emb2}\) are randomly initialized in the beginning of model training.

MTGNN [82] also builds a graph through node embeddings and requires no prior graph structure knowledge. MTGNN models time-series and graphs separately and subsequently incorporates them in a pipeline order. For the sake of conciseness, we focus on the graph modeling part and let \(g_{cnn} (\cdot)\) denote the temporal component, which renders dilated CNN layers to drastically reduce the temporal dimension of time-series. Given time-series data \(\boldsymbol {\mathrm{X}}\in \mathbb {R}^{N \times T \times D}\), node embeddings \(\boldsymbol {\mathrm{H}}_{{emb}_1}, \boldsymbol {\mathrm{H}}_{{emb}_2} \in \mathbb {R}^{N \times d_{emb}}\), the adjacency matrix is computed bywhere two individually calculated node embeddings are transformed by dense layers and a \(\tanh (\cdot)\) activation together with a selected constant hyperparameter \(\alpha\), as shown in Equation (17). Note that \(\boldsymbol {\mathrm{A}}\) is ensured to be asymmetric, and row-wise top K selections are used to further sparsify connections, as formulated in Equation (18).

To preserve the initial graph structure denoted by \(\boldsymbol {\mathrm{A}}\), MTGNN leverages a random walk with restart method to derive multi-level hidden states for each node and thereafter concatenates all hidden states. Let \(\boldsymbol {\mathrm{H}}^0 = g_{cnn} \left(\boldsymbol {\mathrm{X}}\right)\) denote the initial hidden state from the temporal component, the multi-level hidden states are computed and aggregated with the transformed graph structure \(\tilde{\boldsymbol {\mathrm{A}}}\) from Equation (9), resulting in the hidden states at l layer asModel Comparison. STGCN, Graph WaveNet, and MTGNN use different CNN variants for time-series modeling. STGCN uses gated causal CNN and Graph WaveNet uses dilated CNN. MTGNN combines several dilated CNNs to derive the inception dilated CNN, which allows it to model time-series values regarding various granularities. We also notice that STGCN uses a GCN layer to model the provided spatial graph, while Graph WaveNet proposes an adaptive graph that combines both the spatial graph and the self-derived semantic graph. MTGNN only relies on a self-derived semantic graph and requires no provided graph in the datasets. Model Comparison on Time-series Components: RNN versus CNN. To model a time-series in deep learning, one of the most intuitive ways is to apply a fully connected layer or a series of fully connected layers on the input time-series data and update network parameters by fitting predicted values with actual ground truth [5]. Each neuron in the input layer holds a value for each timestep, and neurons in the following layer summarize values at all timesteps by network parameters, however, this leads to an explosive growth of parameters and inefficiency of optimization as the number of layers increases. To address these issues, convolutional layers are more often used, which drastically reduce model complexity with fewer neural connections between layers. Further, a dilated CNN layer (shown in Figure 4) models very long sequences with low model complexity, as it down-samples the time-series input with a pre-selected frequency. CNN-based models are also called direct methods, since they predict future values in one shot [19]; on the contrary, RNN-based models capture the temporal dependency by recurrently consuming the time values to derive a final embedding. Due to this time-series modeling nature, RNN is most widely used in temporal modeling, as we expound on it in Section 3.1. RNN-based graph time-series models nest the graph modeling within the RNN cells and are therefore relatively more constrained regarding the model design, compared to CNN-based models where graph and time-series are separately modeled with different layers, which allows diverse combinations such as the temporal-spatial-temporal structure in STGCN.

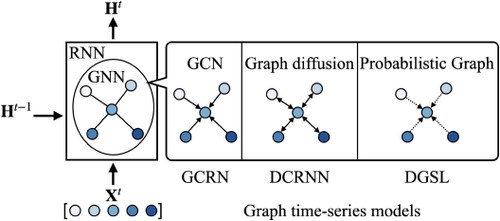
Most related datasets such as traffic data and electricity workload data provide an external graph that primarily describes the geographical connectivity of nodes, however, external graph structures are not always available, and they do not necessarily reflect the actual connections between nodes. In these situations, several models propose using self-derived graphs, i.e., the graph structure is derived either from time-series or from node embeddings. This section describes models from the perspective of graph modeling, specifically, on how different models leverage self-derived graphs to capture the inter-relations between nodes. We discuss three models in this section: FC-GAGA [62], STFGNN [47], and RGSL [91], but other models such as Graph WaveNet and MTGNN, which are discussed in the previous section, also belong to this category. The graph types in different models are summarized in Table 3. At the end of this section, we compare models in terms of their graph modeling.

FC-GAGA [62], similar to MTGNN, requires no prior knowledge of the graph structure. Note that FC-GAGA uses time-series gates instead of RNN or CNN for time-series modeling. The time-series gates can be seen as a special type of CNN, as they are used to weight time co-variate features. Let \(\boldsymbol {\mathrm{X}}\in \mathbb {R}^{N \times T}\) denote the node time-series, and let \(\boldsymbol {\mathrm{H}}_{emb}=f_{EMB}\left(\boldsymbol {\mathrm{X}}\right) \in \mathbb {R}^{N \times d_{emb}}\) denote the node embeddings. FC-GAGA is described by the following equations:where the graph structure \(\boldsymbol {\mathrm{A}}\) is learned and optimized from the node embeddings and is used together with transformed time-series data \(\tilde{\mathbf {x}}_i\) in a gated mechanism to shut off connections of irrelevant node pairs as in Equation (21), with \(\epsilon\) as a selected constant hyperparameter. A hidden state \(\boldsymbol {\mathrm{Z}}\) is constructed from a concatenation of node embedding \(\boldsymbol {\mathrm{H}}_{emb}\), scaled time-series data \(\boldsymbol {\mathrm{X}}/ \tilde{\mathbf {x}}\), and the gated states \(\boldsymbol {\mathrm{G}}\). Subsequently, \(\boldsymbol {\mathrm{Z}}\) serves as the initial input for a residual module, denoted by \(f_{res}\), which generates the time-series prediction \(\hat{\boldsymbol {\mathrm{X}}}\). For the purpose of conciseness, we include the details of the residual module \(f_{res}\) in Section B.2. FC-GAGA benefits from the freedom of automatically deriving graph structures, instead of relying on the Markov model-based or distance-based graph topological information. However, the graph construction from node embedding costs a time complexity of \(\mathcal {O}\left(N^2\right)\), which limits the scalability of FC-GAGA.

STFGNN [47], unlike many models that only use one graph, integrates three graphs with a fusion layer, where each graph encodes one type of information. STFGNN defines a temporal graph \(\boldsymbol {\mathrm{A}}_{t}\) that encodes temporal similarity relationships between graph time-series with a Dynamic Time Warping (DTW) variant (defined in Section C.3), a spatial graph \(\boldsymbol {\mathrm{A}}_{s}\) that is derived from the geographical distance between nodes, and a connectivity graph \(\boldsymbol {\mathrm{A}}_{c}\) that indicates the connections of nodes between two adjacent timesteps. The three matrices are then arranged into a spatial-temporal fusion graph \(\boldsymbol {\mathrm{A}}\in \mathbb {R}^{KN\times KN}\) with a user-selected slice size K for hidden state learning.

RGSL [91] also combines external graph structures and semantic graphs with the aid of the Gumbel-Softmax function. Moreover, RGSL incorporates domain knowledge in the semantic graphs.

Graph Modeling: Goals and Limitations. The objective of graph modeling in graph time-series models is similar to that in ordinary deep graph models, i.e., to effectively and efficiently utilize the neighbor information for each node. Great efforts have been made to allow scalability to address the limitations of time complexity. As a consequence, many GNNs only require \(\mathcal {O}\left(|E|\right)\) [41, 51, 69, 77, 84, 90, 92, 98] instead of \(\mathcal {O}\left(N^2\right)\) [62, 79, 82], hence, graph sparsification on edges significantly reduces time complexity.

In distinction to ordinary deep graph models, the graph structure is strongly related to the time-series in graph time-series models. Researchers should be aware of their constraints, some of which are listed as follows: (a) the graph density can limit the computation efficiency. Although many GNN models reduce the time complexity from \(\mathcal {O} \left(N^2\right)\) to \(\mathcal {O} \left(|E|\right)\), when the graph is dense (a complete graph in the worst case), the number of edges will be close to the square of the number of nodes, i.e., \(\mathcal {O} \left(|E|\right) = \mathcal {O} \left(N^2\right)\), which causes the model to degrade to the worst time complexity. This is a severe limitation for tasks such as time-series forecasting that require a timely response. (b) Moreover, unlike deep learning models whose modeling power generally increases as the depth of the model or the number of layers increases, this does not hold true for deep graph models by simply adding graph neural layers. By stacking many graph neural layers, distant nodes are included and cause the problem of over-smoothing, where the locality information is not well utilized due to message propagation from a large neighborhood set [55, 56, 81, 99]. Graph time-series models, having a nested GNN within an RNN structure, are more susceptible to over-smoothing when modeling long sequences, due to the occurrence of message propagation at each RNN unfolding step. (c) Another problem is over-squashing, which is due to the excessive neighbor nodes information for each node while the learned output is a fixed-length vector, therefore, the loss of information is unavoidable [1]. 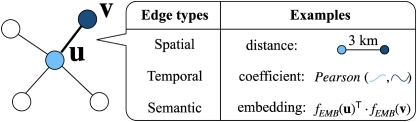Model Comparison on Graph Components: Graph Construction methods. Many graph time-series datasets contain a pre-defined graph. For example, Wikipedia data have a graph that represents the linking relations between sites [75]. In biological networks, a graph is provided to represent the links between bio-entities [19]. However, for other datasets that do not explicitly provide a graph, some metrics are needed to derive one. We describe three ways to derive a graph, namely, the constructions of a spatial graph, a temporal graph, and a semantic graph, respectively. Figure 5 illustrates these graph construction approaches, each accompanied by examples. (a) Spatial Graphs are built on distance information [51]. Directly using distance as edge weights of graphs will cause closer nodes to have smaller edge weights, due to the shorter distance between them. However, most GNN models require a closeness graph where greater edge weights represent stronger connections. One common way to convert a distance graph to a closeness graph is through the radial basis function (RBF) (defined in C.2). A special case is Connectivity Graphs, which are binary, i.e., an edge exists and has the edge weight as 1 between two nodes if and only if they are connected. Under the assumption of the first law of geography, Everything is related to everything else, but near things are more related than distant things, spatial graphs and connectivity graphs are the intuitive choices if they are available in the datasets, as they are used in most models; (b) Temporal Graphs are constructed based on the temporal similarity between node time-series [57]. By formatting each node time-series as a sequence, many sequence similarity metrics can be used to derive a temporal graph, including cosine similarity, coefficient metrics, and Dynamic Time Warping (DTW), among many others. In the aforementioned GRCNN models, for instance, STFGNN [47] uses DTW to derive temporal graphs. Temporal graphs are useful if connections and mutual impacts between nodes are highly correlated to their time-series patterns. Besides, temporal graphs go beyond the first law of geography, as they may connect two highly correlated node time-series that may be geographically distant; (c) Semantic Graphs are constructed based on the node embeddings to connect nodes that are semantically close to each other, that these nodes share some similar hidden features between them [62]. In semantic graphs, spatially distant nodes may share similar features and are closely connected [47]. The level of similarity can be measured by some embedding similarity metric, such as the correlation coefficient. Additionally, the edge embeddings can be used as parameters of distribution functions, from which the edge weights are sampled [70]. It is also possible to integrate more than one semantic type of graph [47, 57]. Semantic graphs have the advantage that they do not rely on external graph structures or time-series patterns. In practice, a combination of various types of graphs is widely used, through cascade processing [62], fusion [47], or using one graph as a mask for another graph [79].

The temporal dynamics are not only limited to lie in the node level time-series but can also exist in evolving graph structures, which induces another level of modeling complexity in graph neural networks. In contrast to a static graph, a series of graphs is used in evolving graph models, denoted by \(\boldsymbol {\mathcal {G}}= (G_1, G_2, \ldots , G_T)\) where there is a graph \(G_t = (V_t, E_t)\) for each timestep t. The number of nodes is dynamically dependent on the timestep \(N_t = |V_t|\). Since the dynamics in evolving graphs are much more complicated to model, this section briefly describes representative models.

Radflow [75] independently models a spatial component and a temporal component and subsequently performs a combination by summing them up. The input of Radflow is a series of graphs \(\mathcal {G}\) and node multivariate time-series \(X\in \mathbb {R}^{N \times T \times d}\). A connectivity graph is derived from the dataset for each timestep, hence, there is a series of adjacency matrices, denoted by a tensor \(A\in \mathbb {R}^{N \times N \times T}\). Radflow consists of following equations:At timestep t, the prediction \(\hat{\boldsymbol {\mathrm{X}}}^t\) is the summation of two variables \(\hat{\boldsymbol {\mathrm{Q}}}^t\) and \(\hat{\boldsymbol {\mathrm{U}}}^t\), which are, respectively, calculated from a recurrent component and a graph component, as illustrated in Equation (24). Both components utilize a residual module and an LSTM model. The graph component uses an extra attention module that is based on the graph attention mechanism and the general attention mechanism. Detailed equations can be found in Section B.3.

Radflow learns node embeddings that are dependent on timesteps and uses them for interpretable prediction and imputation. The graph connectivity information is used to select neighboring nodes for attention computation of each node, without creating trainable parameters over graphs, which makes it relatively lightweight, scalable, and fast compared to GCN-based methods.

TStream [11] adapts GNN models in a continual learning manner to quickly learn expansive evolving network patterns. Under the assumption \(\Delta N_t \ll N_t\), TStream leverages Jensen-Shannon divergence (JSD) to measure the similarity between the distribution of two derived hidden states in adjacent timesteps. Those nodes with high JSD scores are deemed as having drastic changes and are updated together with newly added nodes. An information replay method and a parameter smoothing method are used to avoid historical observations from being forgotten.

LRGCN [46] targets the path classification problem in the time-evolving graphs. The model predicts the possible path failures in the real world, such as those in traffic networks or telecommunication networks. The prediction is based on path embedding, which is an aggregation (by LSTM and attention layers) of all node embeddings along the paths. Z-GCNET [12] proposes a time-aware persistent homology representation learning GCN method to track topological features and use them in traffic forecasting and cryptocurrency price forecasting. ESG [88] claims evolving graph structures vary depending on the time scale of interests, and its proposed model learns a different graph for each time scale. In summary, evolving graph models are more complicated than the previous two models due to their requirement to model the dynamic graph structures, in addition to dynamics of time-series and node relations. A series of graphs is typically given or derived from the datasets, and one key challenge is to handle these graphs without an explosion of parameters.

We discuss six models that use graph attention for time-series forecasting, namely, GaAN [92], Cola-GNN [19], ASTGCN [26], STAG-GCN [57], STGNN [79], and StemGNN [8].

GaAN [92] utilizes a convolutional sub-network to control the importance of each attention head. GaAN added a graph aggregator with a gated characteristic, which is different from that (Equation (11)) of the GAT model, aswith \(\alpha _{ij}^k\) calculated by Equation (10), and \(\mathbf {w}\) the gate vector. \(g_{pool}\) is the designed convolutional sub-network that learns the gate values from node i and its neighboring nodes. For example, GaAN can leverage max pooling and average pooling in \(g_{pool}\). The model is used in both classification and forecasting. When used in time-series forecasting, GaAN can be seen as a GCRN variant with the graph component replaced by the GaAN structure, while the LSTM component is preserved. Cola-GNN [19] leverages the graph attention mechanism in a pairwise manner for influenza-like illness forecasting. ASTGCN [26] fuses various blocks of graph attention layers and temporal attention layers. STAG-GCN [57] is an adaptive gated GCN method for traffic forecasting. STAG-GCN leverages a distance-based spatial graph and a semantic graph that is based on the DTW distance between time-series. STAG-GCN also adopts a general attention mechanism (Equation (33)) for temporal modeling. Similarly, STGNN [79] and StemGNN [8] adopt the general attention mechanism with incorporated states in their spatial component. Most of these forecasting models target regression tasks, however, there are also classification models. For example, THGNN [85] forecasts the direction of stock prediction movement by employing graph structure learning through graph attention and general attention over stock series.

MTAD-GAT [98], GDN [18], and GReLeN [95] target the task of time-series anomaly detection.

MTAD-GAT [98] utilizes GAT models to decide whether there is a time point level anomaly. Given time-series data \(X \in \mathbb {R}^{1 \times T \times d}\), the MTAD-GAT model is described by the following equations:MTAD-GAT is a self-supervised method that leverages GAT from two perspectives: (a) by treating each feature dimension as a node, a GAT model is used to extract relations between features and derives \(\boldsymbol {\mathrm{H}}_d\), and (b) by treating each timestep as a node, another GAT model is used to capture relations between timesteps and derives \(\boldsymbol {\mathrm{H}}_T\). The feature-oriented GAT and the time-oriented GAT are fused with the normalized data, as shown in Equation (27). A GRU structure is used to capture the long-term temporal dependency and derive the final hidden state \(\boldsymbol {\mathrm{H}}\in \mathbb {R}^{T \times d_{hid}}\), as shown in Equation (28). Finally, \(\boldsymbol {\mathrm{H}}\) is fed to a fully connected network and a VAE network to derive a forecasting loss and a reconstruction loss, respectively.

GDN [18] is also a point-level multivariate time-series anomaly detection model, which renders a GAT model to aggregate information from top-k neighbors for each node. Given time-series data \(X \in \mathbb {R}^{N \times T \times d}\), we let \(\boldsymbol {\mathrm{H}}_{emb} \in \mathbb {R}^{N \times d_{emb}}\) denote the initial node embeddings, and the GDN model is described by the following equations:where a binary graph is constructed from the node embedding and is sparsified by selecting top-k neighbors in Equation (29). \(\text{sgn}\) is the sign function and is defined in Section C.5. The hidden state \(H^t_i\) of node i at timestep t is calculated by an attention-based aggregation of node embeddings in the neighborhood, as shown in Equation (30), where pairwise attention scores \(\alpha _{ij}\) are calculated with Equation (10) by taking \([\boldsymbol {\mathrm{H}}_{emb,i} \; f_{FC}\left(X^t_i\right) ]\) as input vectors. Finally, an element-wise multiplication is calculated between the embeddings \(\boldsymbol {\mathrm{H}}_{emb}\) and the hidden states H, after which the result is concatenated and fed through a fully connected network, to derive the binary prediction, as shown in Equation (31).

The node embeddings in GDN have three-fold functions: (a) they are used to construct a binary connectivity graph and (b) they are used to compute pairwise attention scores that essentially represent semantic proximity between nodes, and (c) they are used in final hidden states for forecasting. Without a recurrent component, GDN has the advantage of being more lightweight than other RNN-based graph models. FuSAGNet [29] further enhances anomaly detection performance compared to GDN by uniquely modeling the temporal process for each node embedding, thereby enhancing the model’s robustness.

GReLeN [95] utilizes Variational AutoEncoder (VAE) to model the inter-node dependence for anomaly detection. GReLeN encodes temporal features with general attention and uses to VAE generate a probabilistic graph based on Gumbel-Softmax categorical reparametrization.

Model Comparison on Graph Components: Graph Attention. Graph attention mechanism is proposed to compute the pairwise attention scores between nodes [77]. It is not necessary for GAT to have a pre-defined graph structure; since the graph structure is essentially learned through graph attention, GAT becomes a standardized cornerstone module for many later models. For example, MTAD-GAT leverages GAT to construct a feature-oriented graph and a time-oriented graph for time-series anomaly detection [98]. GDN likewise utilizes a GAT to aggregate node features from neighboring nodes for time-series anomaly detection [18]. Some GAT variants were also proposed, for instance, Cola-GNN builds a GAT-like structure based on the known connectivity information for influenza-like illness forecasting [19]. AGNN [74] uses cosine operation instead of concatenation when calculating attention scores. Temporal Attention and General Attention. In addition to graph attention, temporal attention, and general attention are commonly used in graph time-series modeling. A diagram of these attention mechanisms is depicted in Figure 6.

When using RNN models in sequence-to-sequence forecasting tasks, the hidden state prior to the last timestep from the RNN model, i.e., \(\mathbf {h}^{t-1}, \mathbf {h}^{t-2}, \ldots\), may contribute to the forecasting performance. Attention mechanism is initially proposed to leverage both the latest hidden state and earlier hidden ones by multiplying state values with attention scores [3]. We call this attention type for sequence modeling as a temporal attention mechanism, which takes the form:where the new hidden state \(\mathbf {h}^{\prime t}\) incorporates a sequence of hidden states instead of only the last one. As an example, LSTM-RGCN[49] adopts temporal attention for stock selection.

Since graph time-series models consist of a spatial component and a temporal component, researchers naturally take advantage of graph attention for graph modeling and temporal attention for time-series modeling. For instance, ASTGCN [26] proposes a spatial-temporal block that combines the two attention mechanisms. GMAN [101] also renders the two attention mechanisms and uses a gated fusion to incorporate the resulting states. STHAN-SR [67] uses temporal Hawkes attention and hyper-graph attention for stock selection.

With the success of the temporal attention mechanism, general attention, also called self-attention, was proposed, which describes attention as a function that maps a query and a set of key-value pairs to output [76]. In this line of work, there are three derived variables from the attention embeddings representing query, key, and value states, and an aggregation method is applied to these states. The general attention takes the form:where \(\boldsymbol {\mathrm{Q}}, \boldsymbol {\mathrm{K}}, \boldsymbol {\mathrm{V}}\) are of dimension \(\mathbb {R}^{N \times d_q} , \mathbb {R}^{N \times d_k} , \mathbb {R}^{N \times d_v}\), respectively. Radflow adapts the general attention mechanism with a different aggregation on the query, key, and value states, as described in Equation (53) [75]. STGNN leverages both graph attention and general attention for traffic forecasting [79]. ST-GRAT [66] takes one step further and includes all three types of attention. In addition, attention mechanisms can be used in multi-modal learning. For example, it is possible to fuse attention scores learned from images, text, and historical sales for product sale forecasting [21]. In addition, there are many other types of attention mechanisms based on graphs, such as self-attention [46] and gated attention [92], among others [45].

Time-series built on web view count or video view count have values that cover a large span of values from zero to multiple millions, contrary to traffic speed values that are typically within a small range. To forecast time-series of different scales, scaling is used in data preprocessing and post-processing stages [75]. Min-Max scaling and Z-score scaling are the two most common scaling methods. We list their formulas in Section C.1.

Heterogeneous types of time-series impose another challenge. For example, different types of crimes such as theft or robbery have different time-series patterns and evolving inter-dependency. Attention mechanisms or gate mechanisms can be used to build type-sensitive models and capture the inter-relations between types. Reference [84] proposes a type-aware embedding layer to learn the mutual influence between types of crimes.

In some applications including ride-hailing forecasting and crime forecasting [84], location data are collected based on geographic coordinates instead of pre-selected locations. In this case, grid mapping strategies such as partition and aggregation need to be applied to construct a graph from these data. The grid-structured data can be modeled with CNN to capture the spatial correlations [93] or further aggregated to be modeled with graph models. Besides, graphs in the real world can be dynamic, where the interactions between nodes can change over time. There are several strategies to create a new graph or update an existing graph to reflect the dynamics. For example, STAG-GCN [57] utilizes an adaptive graph that has dynamic edge weights.