Summary
We study the role of partial autocorrelations in the reparameterization and parsimonious modeling of a covariance matrix. The work is motivated by and tries to mimic the phenomenal success of the partial autocorrelations function (PACF) in model formulation, removing the positive-definiteness constraint on the autocorrelation function of a stationary time series and in reparameterizing the stationarity-invertibility domain of ARMA models. It turns out that once an order is fixed among the variables of a general random vector, then the above properties continue to hold and follows from establishing a one-to-one correspondence between a correlation matrix and its associated matrix of partial autocorrelations. Connections between the latter and the parameters of the modified Cholesky decomposition of a covariance matrix are discussed. Graphical tools similar to partial correlograms for model formulation and various priors based on the partial autocorrelations are proposed. We develop frequentist/Bayesian procedures for modelling correlation matrices, illustrate them using a real dataset, and explore their properties via simulations.
Keywords: Autoregressive parameters, Cholesky decomposition, Positive-definiteness constraint, Levinson-Durbin algorithm, Prediction variances, Uniform and Reference Priors, Markov Chain Monte Carlo
1 Introduction
Positive-definiteness and high-dimensionality are two major obstacles in modeling the p × p covariance matrix Σ of a random vector Y = (Y1, ⋯Yp)′. These can partially be alleviated using various decompositions which in increasing order of effectiveness are the variance-correlation (Barnard et al., 2000), spectral (Yang and Berger, 1994;) and Cholesky (Pourahmadi, 1999; Chen and Dunson, 2003) decompositions. Only the latter has the unique distinction of providing an unconstrained and statistically interpretable reparameterization of a covariance matrix, but at the expense of imposing an order among the entries of Y. Three close competitors are, (i) the covariance selection models (Dempster, 1972; Wong et al., 2003) based on full partial correlations obtained from Σ−1, which are statistically interpretable, but constrained, (ii) the logarithm of eigenvalues and logit of Givens angles (Daniels and Kass, 1999; Yang and Berger, 1994) and (iii) the matrix-logarithm models (Chiu et al., 1996). The latter two are based on an unconstrained, but not necessarily interpretable reparameterization of Σ.
We present yet another unconstrained and statistically interpretable reparameterization of Σ using the notion of partial autocorrelation from time series analysis (Box et al., 1994; Pourahmadi, 2001, Chap. 7), which, like the Cholesky decomposition also imposes an order among the entries of Y; this reparamaterization is also ideal for models that directly include correlation matrices, instead of covariance matrices, including multivariate probit models (Chib and Greenberg, 1998) and copulas (Pitt et al., 2006). For covariance matrices, we start with the decomposition Σ = DRD or the variance-correlation strategy (Barnard et al, 2000) and reduce the problem to and focus on reparameterizing a correlation matrix R = (ρij) in terms of a simpler symmetric matrix Π = (πij) where πii = 1 and for i < j, πij is the partial autocorrelation between Yi and Yj adjusted for the intervening (not the remaining) variables. We note that unlike R and the matrix of full partial correlations (ρij), Π has a simpler structure in that it is not required to be positive-definite and hence its entries are free to vary in the interval (−1,1). Furthermore, using the Fisher z transform Π can be mapped to the matrix Π˜ where the off-diagonal entries of the latter take values in the entire real line (−∞, +∞). The process of going from a constrained R to a real symmetric matrix Π˜ is reminiscent of finding a link function in the theory of generalized linear models (McCullagh and Nelder, 1989). Therefore, the analogues of graphical and analytical machineries developed in the contexts of regression and the Cholesky decomposition in Pourahmadi (1999, 2007) and references therein, can be brought to the service of modeling correlation matrices. In the sequel, to emphasize the roles, the properties and the need for (time-) order with a slight abuse of language we refer to Π as the partial autocorrelation function (PACF) of Y or Σ, just as in time series analysis.
Compared to the long history of the use of the PACF in time series analysis (Quenouille, 1949; Daniels, 1956; Barndorff-Nielson and Schou, 1973; Ramsey, 1974; Jones, 1980; Jones 1987), research on establishing a one-to-one correspondence between a general covariance matrix, its PACF and connecting the latter to the entries of the Cholesky factor of the former has a rather short history. An early work in the Bayesian context is due to Eaves and Chang (1992), followed by Zimmerman (2000) and Pourahmadi (1999; 2001, p.102) and Daniels and Pourahmadi (2002) for longitudinal data, and Dégerine and Lambert-Lacroix (2003) for the time series setup. For a general random vector, Kurowicka and Cooke (2003, 2006) and Joe (2006) have relied on graph-theoretical and standard multivariate techniques, respectively. The origins of a fundamental determinantal identity involving the PACF, unearthed recently by these three groups of researchers can be traced to a notable and somewhat neglected paper of Yule (1907, equ. 25) and in the literature of time series in connection with the Levinson-Durbin type algorithms. It plays a central role in Joe's (2006) method of generating random correlation matrices with distributions independent of the order of the indices, and we use it effectively in introducing priors for the Bayesian analysis of correlation matrices. For a similar application in time series analysis, see Jones (1987).
Correlation matrices themselves are accompanied by additional challenges. The constraint of diagonal elements fixed (at one) complicates both reparameterizations, decompositions and computations. Other than the partial correlation parameterization proposed here, there are no unconstrained parameterizations currently in the statistical literature for a correlation matrix. In addition, recent advances in Bayesian computations for correlation matrices (i.e., sampling with Markov chain Monte Carlo algorithms) rely on augmenting the correlation matrix with a diagonal scale matrix to create a covariance matrix (i.e., parameter expansion algorithms). The strategy is to then sample the inverse of this covariance matrix from a Wishart distribution and then transform back to the correlation matrix; see, e.g., Liu (2001) and Liu and Daniels (2006). However, these approaches do not easily extend to structured correlation matrices (as we will discuss here).
The outline of the paper is as follows. In Section 2, we review the recent results in reparameterizing a correlation matrix via PACF and the Cholesky decomposition. We use the latter to derive a remarkable identity expressing determinant of R as a simple function of the partial au-tocorrelations. This identity obtained by Dégerine and Lambert-Lacroix (2003), Joe (2006) and Kurowicka and Cooke (2006), plays a fundamental role in introducing prior distributions for the correlation matrix R which is independent of the order of indices used in defining the PACF. The role of a generalized partial correlogram in formulating parsimonious models for R is discussed and illustrated using Kenward's (1987) cattle data. In Section 3, we introduce new priors for correlation matrices based on this parameterization, examine their properties and relation to other priors that have appeared in the literature (Barnard, et al., 2000), present a simple approach to sample from the posterior distribution of a correlation matrix, and do some simulations to examine the behavior of these new priors. Section 4 provides guidance on use of these models and tools in applications in behavior and social sciences. Section 5 wraps up and provides directions for future work.
2 Reparameterizations of a Correlation Matrix
Modeling correlation matrices and simulating random or “typical” correlation matrices are of central importance in various areas of statistics (Chib and Greenberg, 1998; Barnard et al. 2000; Pan and Mackenzie, 2003; Pitt, Chan, and Kohn, 2006), engineering and signal processing (Holmes, 1991), social and behavior sciences (Liu, Daniels, and Marcus, 2009), finance (Engle, 2002) and numerical analysis (Davies and Higham, 2000). An obstacle in dealing with a correlation matrix R is that all its diagonal entries are the same and equal to one.
In this section, first we reparameterize correlation/covariance matrices of a general random vector Y = (Y1, ⋯, Yp)′ in terms of the partial autocorrelations between Yj and Yj+k adjusted for the intervening variables. Then, using the concept of regression which is implicit in introducing the partial autocorrelations and the Cholesky decomposition of matrices, we point out the connections among the PACF, the generalized autoregressive parameters and the innovation variances of Y introduced in Pourahmadi (1999).
2.1 Reparameterization in terms of Partial Autocorrelations
The notion of PACF is known to be indispensable in the study of stationary processes and situations dealing with Toeplitz matrices such as the Szegö's orthogonal polynomials, trigonometric moment problems, geophysics, digital signal processing and filtering (see Landau, 1987; Pourahmadi, 2001), identification of ARMA models, the maximum likelihood estimation of their parameters (Jones, 1980) and simulating a random or “typical” ARMA model (Jones, 1987). The one-to-one correspondence between the stationary autocorrelation functions {ρk} and their PACF {πk} (Barndorff-Nielsen and Schou, 1973; Ramsey, 1974) makes it possible to remove the positive-definiteness constraint on {ρk}, and work with {πk} which are free to vary over the interval (−1,1) independently of each other.
We parameterize a (non-Toeplitz) correlation matrix R = (ρij) in terms of the lag-1 correlations πi,i+1 = ρi,i+1,i = 1, ⋯, p − 1 and the partial autocorrelations πij = ρij|i+1,⋯,j−1 for j − i ≥ 2, or the matrix Π = (πij). This allows swapping the constrained matrix R by the simpler matrix Π with ones on the diagonal and where for i ≠ j, the πij's can vary freely in the interval (−1,1). The key idea behind this reparameterization is the well-known recursion formula (Anderson, 2003, p.41), see also (1) below, for computing partial correlations in terms of the marginal correlations (ρij). It also lies at the heart of Kurowicka and Cooke (2003, 2006) and Joe (2006) approaches to constructing Π; however the recursive Levinson-Durbin algorithm used by Dégerine and Lambert-Lacroix (2003) will be used in our presentation in Section 2.3.
Following Joe (2006), for j = 1, ⋯, p−k, k = 1, ⋯, p−1, let , and R2(j,k) be the correlation matrix corresponding to the components (j + 1,…, j + k−1). Then, the partial autocorrelations between Yj and Yj+k adjusted for the intervening variables, denoted by , are computed using the expression
| (1) |
In what follows and in analogy with R, it is convenient to arrange these partial autocorrelations in a matrix Π where its (j,j + k)th entry πj,j+k Note that the function g(·) in (1) that maps a correlation matrix R into the partial autocorrelation matrix Π, is indeed invertible, so that solving (1) for ρj,j+k, one obtains
| (2) |
where Djk is the denominator of the expression in (1). Then, the formulae (1)-(2) clearly establish a one-to-one correspondence between the matrices R and Π. In the sequel, with a slight abuse of language and following the tradition in times series analysis we refer to the matrix Π or πj,j+k viewed as a function of (j, k), as the partial autocorrelation function (PACF) of Y.
Evidently, when R is a stationary (Toeplitz) correlation matrix, then πj,j+k depends only the lag k, see (1). Consequently, Π is a stationary (Toeplitz) matrix. Fortunately, the converse is also true and follows from (2). For ease of reference, we summarize these observation in Lemma 1 in Section 2.3. A correlation matrix R is stationary (Toeplitz) if and only if its associated PACF Π is a stationary (Toeplitz) matrix.
Moreover, for a stationary correlation matrix, R reduces precisely to the celebrated Levinson-Durbin formula (Pourahmadi, 2001, Theorem 7.3) for computing the PACF recursively.
2.2 An Alternative Reparameterization: Cholesky Decomposition
Next, we present an alternative reparameterization of a covariance matrix via its Cholesky decomposition or the idea of autoregression for the underlying random vector.
Consider a mean-zero random vector Y with the positive-definite covariance matrix Σ = (σst). For1 ≤ t ≤ p, let Ŷt be the linear least-squares predictor of Yt based on its predecessors Y1, ⋯, Yt−1 and let εt = Yt −Ŷt be its prediction error with variance . Then, there are unique scalars φtj so that or
| (3) |
Let ε = (ε1, ⋯, εp)′ be the vector of successive uncorrelated prediction errors with . Then, (3) rewritten in matrix form becomes ε = TY, where T is a unit lower triangular matrix with 1's on the main diagonal and −φtj in the (t,j)th position for 2 ≤ t ≤ p, j = 1, ⋯, t −1. Note that is different from σtt = Var(Yt) However, when the responses are independent, then φtj = 0 and , so that the matrices T and D gauge the “dependence” and “heterogeneity” of Y, respectively.
Computing covariances using ε = TY, it follows that
| (4) |
The first factorization in (4), called the modified Cholesky decomposition of Σ, makes it possible to swap the p(p + 1)/2 constrained parameters of Σ with the unconstrained set of parameters φtj and log of the same cardinality. In view of the similarity of (3) to a sequence of varying order autoregressions, we refer to the parameters φtj and as the generalized autoregressive parameters (GARP) and innovation variances (IV) of Y or Σ (Pourahmadi, 1999). A major advantage of (4) is its ability to guarantee the positive-definiteness of the estimated covariance matrix given by T̂−1D̂T̂′−1 so long as the diagonal entries of D̂ are positive.
It should be noted that imposing structures on Σ will certainly lead to constraints on T and D in (4). For example, a correlation matrix R with 1's as its diagonal entries is structured with possibly p(p − 1)/2 distinct parameters. In this case, certain entries of T and D are either known, redundant or constrained. In fact, it is easy to see that the diagonal entries of the matrix D for a correlation matrix are monotone decreasing with For this reason and others, it seems more prudent to rely on the ordered partial correlations when reparameterizing a correlation matrix R as in Section 2.1, than using its Cholesky decomposition.
2.3 A Multiplicative Determinantal Identity: Partial Autocorrelations
First, we study the role of partial autocorrelations in measuring the reduction in prediction error variance when a variable is added to the set of predictors in a regression model. Using this and the second identity in (4) we obtain a fundamental determinantal identity expressing |Σ| in terms of the partial autocorrelations and diagonal entries of Σ. Joe (2006) and Kurowicka and Cooke (2006) had obtained this identity using determinantal recursions and graph-theoretical methods based on (1), respectively. An earlier and a slightly more general determinantal identity for covariance matrices in the context of nonstationary processes was given by Dégerine and Lambert-Lacroix (2003, p.54), using an analogue of the Levinson-Durbin algorithm.
For u and v two distinct integers in {1, 2, ⋯, p}, let L be a subset of {1, 2, ⋯, p}\{u, v} and πuv|L stand for the partial correlation between Yu and Yv adjusted for Yℓ, ℓεL. We denote the linear least squares predictor of Yu based on Yℓ, ℓεL by Ŷ u|L, and for v an integer Lv stands for the union of the set L and the singleton {v}.
Lemma 1. Let Y = (Y1, ⋯, Yp)′ be a mean-zero random vector with a positive-definite covariance matrix Σ. Then, with u,v and L as above, we have
(5) (6)
Proof. (a) Let sp{Yu; uεL} stand for the linear subspace generated by the indicated random variables. Since Yv − Ŷv|L is orthogonal to sp{Yu; uεL} it follows that
and from the linearity of the orthogonal projection we have
where αuv, the regression coefficient of Yu on Yv − Ŷv|L is given by
Since Ŷu|Lε sp{Yi; iεL} is orthogonal to Yv − Ŷv|L, the numerator of the expression above can be replaced by Cov(Yu −Ŷ u|L, Yv −Ŷv|L), so that
(b) From the first identity in (5), it is immediate that
or
| (7) |
Computing variances of both sides of (7) and using the fact that Yu −Ŷu|Lv is orthogonal to Yv−Ŷv|L, it follows that
Now, substituting for αuv from (a), the desired result follows.
Next, we use the recursion (6) to express the innovation variances or the diagonal entries of D in terms of the partial correlations or the entries of π. Similar expressions for φtj's, the entries of T, are not available. The next theorem sheds some light on this problem. Though the expressions are recursive and ideal for computation (Levinson-Durbin algorithm), they are not as explicit or revealing. The approach we use here is in the spirit of the Levinson-Durbin algorithm (Pouramadi, 2001, Corollary 7.4) as extended by Dégerine and Lambert-Lacroix (2003) to nonstationary processes.
Theorem 1. Let Y = (Y1, ⋯, Yp) be a mean-zero random vector with a positive-definite covariance matrix Σ which can be decomposed as in (4).
-
Then, for t = 2, ⋯, p; j = 1, ⋯, t − 1, we have
-
For t = 2, ⋯, p; L = {2, ⋯, t − 1}
φtj = φtj|L − φt1φ1,t−j|L, for j = 2, ⋯, t −1,
where φtj|L and φ1,t−j|L are, respectively, the forward and backward predictor coefficients of Yt and Y1 based on {Yk; kεL}, defined by
Proof (a) follows from the repeated use of (6) with u = t and v = j,j = 1, ⋯, t −1. (b) follows from (4) and (a).
Part (c) proved first in Pourahmadi (2001, p.102) shows that only the entries of the first column of T are multiples of the ordered partial correlations appearing in the first column of π. However, for j > 1, since φtj is a multiple of the partial correlation between Yj and Yt adjusted for {Yi; i ε [1, t)\{j}}, (see Lemma 1(a)), it is not of the form of the entries of π. Note that these observations are true even when Y is stationary or Σ is Toeplitz (Pourahmadi, 2001, Lemma 7.8 and Theorem 7.3). In the search for connection with the entries of π, it is instructive to note that the nonredundant entries of T−1 = (θtj) can be interpreted as the generalized moving average parameters (GMAP) or the regression coefficient of εj when Yt is regressed on the innovations εt, ⋯, εj, ⋯, ε1, see Pourahmadi (2001, p.103). An alternative interpretation of θtj as the coefficient of Yj when Yt is regressed on Yj, Yj−1, ⋯, Y1 is presented in Wermuth et al. (2006 Sec. 2.2). Consequently, θtj is a multiple of the partial correlation between Yt and Yj adjusted for {Y1, ⋯, Yj−1}. We hope these connections and working with partial correlations will offer similar advantage to working with the GARP in terms of the autoregression interpretation (Pourahmadi, 2001, Sections 3.5.3 and 3.5.4).
2.4 An Attractive Property of the PACF parameterization
Parsimonious modeling of the GARP of the modified Cholesky decomposition often relies on exploring for structure as a function of lag; for example, fitting a polynomial to the GARP as a function of lag (Pourahmadi, 1999). For such models, the GARP, in a sense, have different interpretations within lag; i.e., the lag 1 coefficient from the regression of Y3 on (Y2, Y1) is the Y2 coefficient, when another variable, Y is also in the model; however, for the regression of Y2 on Y1, the lag 1 coefficient is the Y1 coefficient with no other variable in the model. So, for a given lag k, the lag k coefficients all come from conditional regressions where the number of variables conditioned on are different. However, by construction, the lag k partial autocorrelations are all based on conditional regressions where the number of conditioning variables are the same, always conditioning on k − 1 intervening variables. This will facilitate building models for the partial autocorrelations as a function of lag. We discuss such model building in the next section.
2.5 Parsimonious Modeling of the PACF
In this section, we use the generalized partial correlogram, i.e. the plot of {πj,j+k; j = 1, ⋯, p−k} versus k = 1, ⋯, p−1, as a graphical tool to formulate parsimonious models for the PACF in terms of the lags and other covariates. If necessary, we transform its range to the entire real line using z transform. Such modeling environment is much simpler and avoids working with the complex constraints on the correlation matrix R (Barnard et al., 2000; Daniels and Normand, 2006) or the matrix of full partial correlations constructed from Σ−1 (Wong et al. 2003); note that the full partial correlations are defined as the correlation between two components conditional on all the other components.
Note that the partial autocorrelations πj,j+k between successive variables Yj and Yj+k are grouped by their lags k = 1, ⋯, p−1, and heuristically, πj,j+k gauges the conditional (in)dependence between variables k units apart conditional on the intervening variables, so one expects it to be smaller for larger k. In the Bayesian framework, this intuition suggests putting shrinkage priors on the partial autocorrelations that shrink the matrix Π toward certain simpler structures (Daniels and Kass, 2001).
2.6 Data illustration
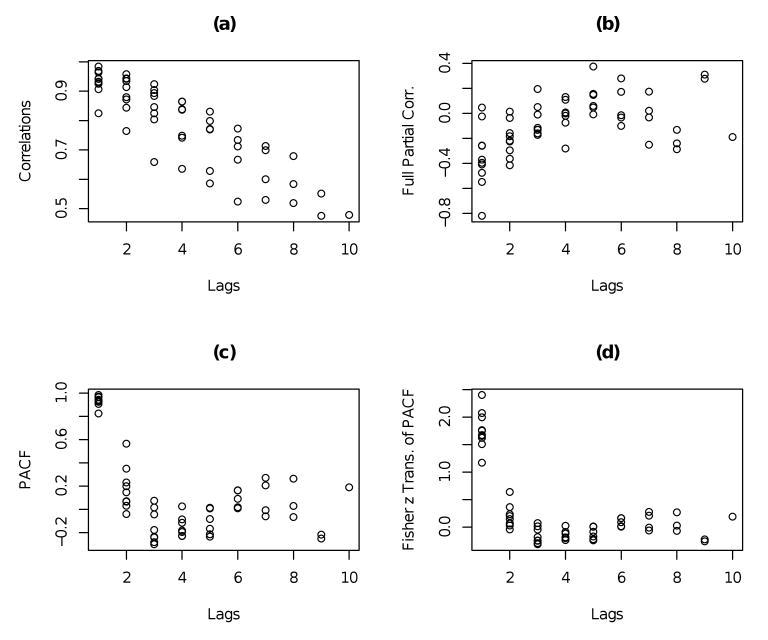
To illustrate the capabilities of the generalized correlograms in revealing patterns, we use the cattle data (Kenward, 1987) which consists of p = 11 bi-weekly measurements of the weights of n = 30 cows. Table 1, displays the sample (partial) correlations for the cattle data in the lower (upper) triangular segment and the sample variances are along the main diagonal. It reveals several interesting features of the dependence in the data that the commonly used profile plot of the data cannot discern. For example, note that all the correlations are positive, they decrease monotonically within the columns (time-separation), they are not constant (nonstationary) within each subdiagonal. In fact, they tend to increase over time (learning effect). Furthermore, the partial autocorrelations of lags 2 or more are insignificant except for the entries 0.56 and 0.35.
Table 1.
Cattle Data. Sample correlations (below the main diagonal), sample PACF (above the main diagonal) and sample variances (along the main diagonal).
| 106 | 0.82 | 0.07 | -0.24 | 0.03 | 0.01 | 0.16 | -0.06 | 0.26 | -0.22 | 0.19 |
| 0.82 | 155 | 0.91 | 0.03 | 0.02 | -0.23 | -0.17 | 0.01 | -0.01 | -0.07 | -0.25 |
| 0.76 | 0.91 | 165 | 0.93 | 0.07 | -0.04 | -0.12 | 0.01 | 0.09 | 0.21 | 0.03 |
| 0.66 | 0.84 | 0.93 | 185 | 0.94 | 0.23 | -0.18 | -0.2 | -0.22 | 0.02 | 0.27 |
| 0.64 | 0.80 | 0.88 | 0.94 | 243 | 0.94 | -0.04 | 0.07 | -0.23 | -0.08 | 0.16 |
| 0.59 | 0.74 | 0.85 | 0.91 | 0.94 | 284 | 0.93 | 0.56 | -0.3 | -0.09 | -0.24 |
| 0.52 | 0.63 | 0.75 | 0.82 | 0.87 | 0.93 | 306 | 0.93 | 0.35 | -0.24 | -0.18 |
| 0.53 | 0.67 | 0.77 | 0.84 | 0.89 | 0.94 | 0.93 | 341 | 0.97 | 0.15 | -0.28 |
| 0.52 | 0.60 | 0.71 | 0.77 | 0.84 | 0.90 | 0.93 | 0.97 | 389 | 0.96 | 0.2 |
| 0.48 | 0.58 | 0.70 | 0.73 | 0.80 | 0.86 | 0.88 | 0.94 | 0.96 | 470 | 0.98 |
| 0.48 | 0.55 | 0.68 | 0.71 | 0.77 | 0.83 | 0.86 | 0.92 | 0.96 | 0.98 | 445 |
Figure 1 presents the generalized correlograms corresponding to the sample correlation matrix of the data, the full partial correlations, the generalized partial correlogram and the Fisher's z transform of the PACF. Note that the first two correlograms suggest linear and quadratic patterns in the lag k, but in fitting such models one has to be mindful of the constraints on the coefficients so that the corresponding fitted correlation matrices are positive definite. Details of fitting such models and the ensuing numerical results can be found in Pourahmadi (2001). The generalized partial correlogram in (c) reveals a cubic polynomial in the lags, i.e. πj,j+k = γ0 + γ1k + γ2k2 + γ3k3; in fitting such models the only constraint to observe is that the entries of the matrix Π are required to be in (−1,1). However, the Fisher z transform of the entries of Π are unconstrained and Figure 1(d) suggests a pattern that can be approximated by an (exponential) function α + β exp(−k), k = 1, ⋯, p−1, with no constraints on (α, β) or another cubic polynomials in the lags. The least-squares fits of a cubic polynomial and an exponential function to the correlograms in Figure 1 (c)-(d) are summarized in Table 2. Note that fitting such models to the PACF amounts to replacing the entries of the kth subdiagonal of the matrix Π by a single number and hence R is approximated by a stationary (Toeplitz) matrix, see Lemma 1 and Theorem 2 below. In addition, this parameterization also allows the marginal variances to be similarly modelled parsimoniously (as a function of time) similar to the modelling of the prediction variances in Pourahmadi (1999). The maximum likelihood estimation of the parameters and their asymptotic properties will be pursued in a future work.
Figure 1.
(a) Generalized sample correlogram for the cattle data, (b) Generalized inverse correlogram, (c) Generalized partial correlogram, (d) Plot of Fisher z transform of the PACF.
Table 2.
Fitted PACF from the least-squares fit of a cubic polynomial to the sample PACF (first row) and the fitted Fisher's z transform of PACF from the least-squares fit of an exponential function of the lags (second-row).
| Lags | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Fitted PACF | 0.89 | 0.24 | -0.09 | -0.19 | -0.15 | -0.02 | 0.11 | 0.16 | 0.07 | -0.26 |
| Fitted z transf. | -1.64 | -0.49 | -0.07 | .09 | 0.15 | 0.17 | 0.18 | 0.18 | 0.18 | 0.18 |
3 Priors for R via the partial autocorrelations
In addition to the advantages for formulating parsimonious models, the unconstrainedness of the PACF suggests some approaches for constructing priors for R using independent linearly transformed Beta priors on (−1,1) for the PACF.
3.1 Independent priors on partial autocorrelations
Given that each partial autocorrelation is free to vary in the interval (−1,1), we may construct priors for R derived from independent priors on the PACF. For example, independent Unif[-1,1] priors (IU priors) on the partial autocorrelations (Jones, 1987; Joe, 2006) can be shown to induce the following prior on the correlation matrix R:
| (8) |
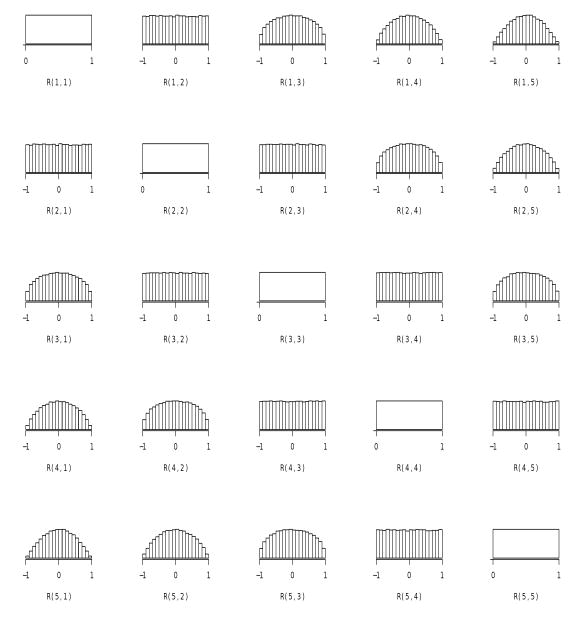
One can express the prior in (8) in terms of the marginal correlations, ρj,j+k by plugging in for πj,j+k from (1). This prior induces a particular behavior on the marginal correlations. Specifically, the priors on the (marginal) correlations ρj,j+k, become gradually more peaked at zero as the lag k grows. As an illustration of this behavior, Figure 2 shows the histograms based on 10,000 simulations from the uniform prior on the partial autocorrelations for p = 5. As the dimension p of the correlation matrix grows, the priors become more peaked at zero for larger lags. This can also be seen by examining the prior probability of being in some interval, say [−.5, .5], as a function of the lag. For p = 15, the (averaged) probabilities, ordered from lag 1 to lag 14, are respectively, (.50, .59, .65, .70, .73, .76, .78, .80, .82, .83, .84, .85, .86, .87). This would appear to be a desirable behavior for longitudinal data which typically exhibits serial correlation decaying with increasing lags.
Figure 2.
Marginal priors on ρjk from independent uniform priors on the partial correlations, πjk. The subplots are arranged as the matrix R.
It is also evident from Figure 2 that the priors for ρj,j+k with k fixed, appear to be the same (see the subdiagonals). We state this observation more formally in the following theorem; see also Lemma 1.
Theorem 2. The partial autocorrelations, πj,k have independent “stationary” priors, i.e
| (9) |
(or the priors are the same along the subdiagonals of Π), if and only if the marginal priors on the correlations ρjk are also “stationary”, i.e.
| (10) |
(or the priors are the same along the corresponding subdiagonal of R).
This implies that “stationary” priors on Π induce “stationary” priors on the marginal correlations and vice versa. Most priors we introduce here satisfy this property.
More generally independent linearly transformed Beta priors on the interval (-1,1) for partial correlations are a convenient and flexible way to specify a prior for a correlation matrix R. These priors, denoted by Beta(α,γ), have the density
| (11) |
Interestingly, the uniform prior on the correlation matrix (Barnard et al, 2000) corresponds to the following stationary Beta priors on the partial correlations:
| (12) |
where ; see Joe (2006). We will refer to this prior as Barnard Beta (BB). As noted in Barnard et al. (2000), such a prior on R results in the marginal priors for each of the marginal correlations being somewhat peaked around zero (same peakedness for all ρjk). Also note that the priors become more peaked as p grows.
In general, priors for the correlation matrix proportional to powers of the determinant of the correlation matrix,
| (13) |
are constructed by setting in (12) Priors so constructed are proper, so improper priors like Jeffreys' for a correlation matrix in a multivariate normal model, π (R) = |R|−(p+1)/2, are not special cases.
3.2 Shrinkage behavior of the BB and IU priors
The IU priors on the PACF induce desirable behavior for longitudinal (ordered data) by ‘shrinking’ higher lag correlations toward zero. The Beta priors in (12), which induce a uniform prior for R (BB priors) place a uniform (-1,1) prior on the lag p − 1 partial autocorrelations and shrink the other partial autocorrelations toward zero with the amount of shrinkage being inversely proportional to lag. This induces the desired behavior on the marginal correlations, making their marginal priors equivalent, but it is counter-intuitive for ordered/longitudinal data with serial correlation; in addition, the shrinkage of the lag one partial autocorrelations for the BB prior increases with p (recall the form in (12)). In such data, we would expect lower lag correlations to be less likely to be zero and higher lag correlations to be more likely to be zero. Thus, the independent uniform priors are likely a good default choice for the partial autocorrelations in terms of inducing desirable behavior on the marginal correlations and not counter-intuitively shrinking the partial autocorrelations. We explore this shrinkage behavior further via some simulations in Section 3.5.
In addition, we expect many of the higher lag partial correlations to be close to zero for longitudinal data with serial correlation via conditional independence (see Table 1). To account for this, we could (aggressively) shrink the partial autocorrelations toward zero (with the shrinkage increasing with lag) using shrinkage priors similar to those proposed in Daniels and Pourahmadi (2002) and Daniels and Kass (2001) or by creating such priors based on the Beta distributions proposed here. We are currently exploring this.
3.3 Some other priors for a correlation matrix
Other priors for R have been proposed in the literature which cannot be derived based on independent priors on the partial autocorrelations. For example, the prior on R that induces marginal uniform (-1,1) priors on the ρij's (Barnard et al., 2000) has the form:
| (14) |
where R[−i,−i] is the submatrix of R with the ith row and column removed and . Such a prior might not be a preferred one for longitudinal (ordered) data where the same marginal priors on all correlations (irrespective of lag) may not be the best default choice.
Eaves and Chang (1992) derived some related reference priors for the set of partial correlations, π1,j for j = 2,…, p; however, their priors are not natural for longitudinal data. Chib and Greenberg (1998) specified a truncated multivariate normal distribution on the marginal correlations. Liechty et al. (2004) placed normal distributions on the marginal correlations with the goals of grouping the marginal correlations into clusters. The latter two priors along with those in Wong et al. (2003) for the full partial correlations (pij) are highly constrained given that they model the marginal correlations directly.
3.4 Bayesian Computing
An additional issue with modeling the correlation matrix is computational. Our development here will focus on cases without covariates in the correlation matrix (this will be left for future work) under the class of independent priors on the PACF discussed in Section 3.1. The proposal here might be viewed as an alternative to the PX-RPMH algorithm in Liu and Daniels (2006) that explicitly exploits the fact that we are modeling the partial correlations themselves (a computational comparison will be left for future work). However, our approach will naturally allow structures in the partial correlations which cannot be done when using current versions of the PX-RPMH (or similar) algorithms; for example, if the partial autocorrelations are zero or constant within lag since then the correlation matrix is highly constrained.
In the following, we assume the data, {Yi : i = 1,…, n}are independent, normally distributed p-vectors with mean Xiβ and with covariance matrix Σ = R (a correlation matrix). A natural way to sample the partial autocorrelations is via a Gibbs sampling algorithm in which we sample from the full conditional distributions of each of the partial autocorrelations. Given that the full conditional distributions of the partial autocorrelations are not available in closed form there are several options to sample them. We explore a simple one next.
We propose to use an auxiliary variable approach to sample each partial autocorrelation. Define the likelihood for the partial autocorrelation, πjk as L(πjk) and the prior as p(πjk). As in Damien et al. (1999), introduce a positive latent variable Ujk such that
| (15) |
To sample πjk we can proceed in two steps,
Sample Ujk ∼ Unif(0,L(πjk)).
Sample p(πjk) constrained to the set {πjk : L(πjk) > Ujk}.
Truncated versions of the priors proposed here, linearly transformed Beta distributions (of which the uniform is a special case), can easily be sampled using the approach in Damien and Walker (2001). The truncation region for step 2, given that the domain of πjk is bounded, can typically be found quickly numerically.
The likelihood evaluations needed to find the truncation interval can be made simpler by taking advantage of the following facts.
Fact 1. If we factor R−1 = CPC, where P is a correlation matrix and C is a diagonal matrix, the elements of P are the full partial correlations, pij|rest (Anderson, 1984, Chapter 15).
Fact 2. To isolate the likelihood contribution of πj,j+k, we can factor the entire multivariate normal distribution into p(yj,…, yj+k)p(yl : l < j or l > j + k | yj,…, yj+k). The (l,k) entry of inverse of the correlation matrix, R[j : j +k] for the first factor is related to the partial correlation of interest (recall Fact 1).
Fact 3. Using the determinantal identity in Theorem 1(b), the determinant of submatrices of R in terms of partial correlations can be written as a function of the partial correlations,
| (16) |
It can be shown that the likelihood in terms of one of the partial correlations of interest, say πjk, can be written as
| (17) |
where Sy[j : k] is the submatrix of Σi(yi−Xiβ)(yi−Xiβ)′ and R[j : k] is the submatrix of R based on the first component of the factorized distribution in Fact 2. above.
Extensions of these computational procedures to modelling the correlation matrix when the matrix of interest is a covariance matrix is straightforward (see, e.g., Liu and Daniels, 2006).
3.5 Simulations
We now conduct some simulations in a longitudinal setting to
examine the mixing behavior of the auxiliary variable sampler here and
compare the risk of the IU prior to the BB prior, the standard default prior for a correlation matrix.
In terms of the mixing of the Markov chain, the auxiliary variable sampler on the partial autocorrelations works quite well, with the lag correlation in the chain dissipating quickly. For example, for p = 5, n = 20, the lag correlations for each partial autocorrelation was negligible by lag 10. Similar results were seen for other p/n combinations.
For our simulation, we consider three true matrices representing typical serial correlation, an AR(1) with lag 1 correlation of .8 and one with lag correlation .6. Both these matrices have all partial autocorrelation beyond lag 1 equal to 0. We also considered a matrix that had more non-zero partial autocorrelations with lags 1,2,3,4 equal to (.8, .4, .1,0) respectively. We consider two size matrices/sample size combinations, p = 5 with n = 10,25,50,100 and p = 10 with sample sizes, n = 20,50,100. We also consider several loss functions, log likelihood (LL) loss, tr(R̂R−1) − log|R̂R−1| −p, with Bayes estimator the inverse of the posterior expectation of R−1 and squared error loss on Fisher's z-transform of the partial autocorrelations, πjk (SEL-P) and the marginal correlations, ρjk (SEL-M), with Bayes estimator the posterior mean (of the z-transformed correlations).
For p = 5, the risk reductions from the IU prior are clear from Table 3, with percentage reductions as large as 30% for n = 10, 20% for n = 25 and 10% for n = 50. For p = 10, the risk reductions from the uniform prior are clear from Table 4, with percentage reductions as large as 40%. The largest risk reductions were for loss SEL-M (squared error loss on the Fisher's z-transform on the marginal correlations). The lower risk reductions for the first order autoregressive covariance matrices are related to only the lag 1 partial autocorrelations being non-zero; so the shrinkage of the BB prior for all the other partial autocorrelations is not unreasonable. Examination of squared error loss for the partial autocorrelations by lag indicates large reductions for the lag 1 partial autocorrelations and small increases for the other lag partial autocorrelations.
Table 3.
Results for p = 5. Each row corresponds to n = 10, 25, 50, 100. IU: independent uniform priors; BB: Barnard Beta priors. LL: log likelihood loss; SEL-P: squared error loss on Fisher's z-transformation of the partial autocorrelations; SEL-M: squared error loss on Fisher's z-transformation of the marginal correlations. Full: matrix with lag 1-3 partial autocorrelations equal to (.8, .4, .1) with the rest zero.
| LL | SEL-P | SEL-M | ||||
|---|---|---|---|---|---|---|
| R | IU | BB | IU | BB | IU | BB |
| AR(.8) | 1.02 | 1.40 | .71 | .87 | .97 | 1.33 |
| .38 | .46 | .29 | .33 | .30 | .39 | |
| .20 | .22 | .16 | .18 | .15 | .18 | |
| .09 | .10 | .08 | .08 | .06 | .07 | |
| AR(.6) | .74 | .78 | .63 | .65 | .74 | .78 |
| .34 | .36 | .30 | .32 | .31 | .33 | |
| .18 | .19 | .16 | .16 | .15 | .16 | |
| .10 | .10 | .08 | .09 | .08 | .09 | |
| Full | 1.24 | 1.60 | .78 | .95 | 1.29 | 1.80 |
| .40 | .47 | .30 | .33 | .34 | .45 | |
| .21 | .23 | .17 | .18 | .15 | .18 | |
| .10 | .11 | .08 | .09 | .08 | .09 | |
Table 4.
Results for p = 10. Each row corresponds to n = 20, 50, 100. IU: independent uniform priors; BB: Barnard Beta priors. LL: log likelihood loss; SEL-P: squared error loss on Fisher's z-transformation of the partial autocorrelations; SEL-M: squared error loss on Fisher's z-transformation of the marginal correlations. Full: matrix with lag 1-3 partial autocorrelations equal to (.8, .4, .1) with the rest zero.
| LL | SEL-P | SEL-M | ||||
|---|---|---|---|---|---|---|
| R | IU | BB | IU | BB | IU | BB |
| AR(.8) | 1.50 | 1.90 | 1.42 | 1.56 | 1.55 | 2.27 |
| .72 | .81 | .68 | .73 | .64 | .85 | |
| .40 | .44 | .37 | .40 | .32 | .41 | |
| AR(.6) | 1.37 | 1.42 | 1.44 | 1.41 | 1.44 | 1.56 |
| .69 | .71 | .69 | .69 | .68 | .72 | |
| .40 | .41 | .39 | .40 | .36 | .38 | |
| Full | 1.61 | 2.08 | 1.45 | 1.63 | 2.15 | 3.56 |
| .74 | .85 | .69 | .74 | .66 | .99 | |
| .40 | .44 | .37 | .39 | .30 | .40 | |
In addition, the estimates of the first order lag correlation themselves show large differences (not shown). For AR(.8) with p = 10 and n = 20, the means were .76 under the IU prior and about .71 under the BB prior with similar discrepancies for p = 5.
Some of the risk reductions from using the IU priors on the partial autocorrelations are small. However, they come at no computational cost (unlike some priors for covariance matrices proposed in the literature) and are consistent with prior beliefs about partial autocorrelations representing serial correlation. The BB prior is not a good default choice due to its dampening effects on the important lower order partial autocorrelations. Further risk improvement might be expected through the use of more targeted shrinkage (Daniels and Pourahmadi, 2002).
4 Partial correlations in the behavior and social sciences
The models and priors for partial correlations are extremely important for many applications involving longitudinal and functional data in the behavior and social sciences. In particular, modeling longitudinal data using structural equation and factor analytic models (i.e., latent variable models in general) typically require careful modeling of correlation matrices (see e.g., Daniels and Normand, 2006) as do multivariate probit models (Chib and Greenberg, 1998; Czado, 2000; Liu, Daniels, and Marcus, 2009). The tools here provide both a general class of methods for using the ordered partial correlations that allow parsimonious modeling of correlations via regression modeling and sensible priors on correlations within such models which is often essential in small to medium sized datasets. Such modeling takes on even more importance in the presence of incomplete data (Daniels and Hogan, 2008). In addition, the uniform priors on the partial correlations recommended in Section 3 provide no additional computational challenges over standard priors for a correlation matrix. Future work will illustrate these methods more fully in applications.
5 Discussion
Using the variance-correlation separation strategy, modeling a covariance matrix is reduced to that of its correlation matrix R which has the additional constraint that all its diagonal entries must equal to one. Though the Cholesky decomposition can handle the positive-definiteness, it cannot be applied directly when there are additional constraints such as stationarity or constancy along diagonals (Pourahmadi, 1999, Sec. 2.6), zero entries (Chaudhuri, Drton and Richardson, 2007) and separable covariance structures (Lu and Zimmerman, 2005). The reparameterization in terms of partial autocorrelations is shown to work well in the face of an additional constraint. It requires ordering the variables which is not a problem for longitudinal and functional data, but might be difficult to justify for other situations. Related work on trying to ‘order’ data that does not have a natural ordering can be found in Stein et al (2004) and Berger and Bernardo (1992). The long history and successful use of the PACF in the time series literature provide valuable graphical and analytical tools which can be generalized to the nonstationary setup.
Given the conditioning structure of the partial autocorrelations, we expect many of them to be zero (see Table 1). Thus, it would be natural to adapt the approach in Wong, Carter, and Kohn (2003) to zero out the partial correlations. We might expect computational simplifications given that the PACF are free to vary independently in [−1, 1] unlike the full partial correlations. In addition, when constructing priors for the probability of a partial autocorrelation being zero, the lack of exchangeability of the partial autocorrelations (vs. the full partial correlations) given that they condition on different numbers of variables (i.e., only the intervening variables) must be taken into account; such issues have been addressed in Liu et al. (2009) in a related setting.
We will explore the computational efficiency of other proposals for Bayesian computing in future work, including sampling all the partial autocorrelations together. In addition, we will derive strategies for Bayesian inference when modeling Fisher's z transform of the partial autocorrelations as a function of covariates.
Acknowledgments
We thank Yanpin Wang for coding the simulations. This research was partially funded by grants from NIH (Daniels) and NSF (Pourahmadi).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
M.J. Daniels, Email: mdaniels@stat.ufl.edu, Department of Statistics, University of Florida.
M. Pourahmadi, Email: pourahm@math.niu.edu, Division of Statistics, Northern Ill. University.
References
- Anderson TW. An Introduction to Multivariate Statistical Analysis. John Wiley & Sons; 1984. [Google Scholar]
- Barnard J, McCulloch R, Meng X. Modeling covariance matrices in terms of standard deviations and correlations, with applications to shrinkage. Statistica Sinica. 2000;10:1281–1312. [Google Scholar]
- Barndorff-Nielsen O, Schou G. On the parameterization of autoregressive models for partial autocorrelation. J of Multivariate Analysis. 1973;3:408–419. [Google Scholar]
- Berger JO, Bernardo JM. On the development of reference priors. In: Bernardo JM, Berger JO, Dawid AP, Smith AFM, editors. Bayesian Statistics 4: Proceedings of the Fourth Valencia Meeting; Clarendon Press; 1992. pp. 35–49. [Google Scholar]
- Box GEP, Jenkins GM, Reinsel GC. Time Series Analysis-Forecasting and Control. Revised 3rd. Prentice Hall; NJ: 1994. [Google Scholar]
- Chen Z, Dunson D. Random effects selection in linear mixed models. Biometrics. 2003;59:159–182. doi: 10.1111/j.0006-341x.2003.00089.x. [DOI] [PubMed] [Google Scholar]
- Chib S, Greenberg E. Analysis of multivariate probit models. Biometrika. 1998;85:347–361. [Google Scholar]
- Chaudhuri S, Drton M, Richardson TS. Estimation of a covariance matrix with zeros. Biometrika. 2007;94:199–216. [Google Scholar]
- Chiu TYM, Leonard T, Tsui KW. The matrix-logarithm covariance model. Journal of the American Statistical Association. 1996;91:198–210. [Google Scholar]
- Czado C. Multivariate regression analysis of panel data with binary outcomes applied to unemployment data. Statistical Papers. 2000;41:281–304. [Google Scholar]
- Damien P, Wakefield J, Walker SG. Gibbs sampling for Bayesian non-conjugate and hierarchical models by using auxiliary variables. Journal of the Royal Statistical Society, Series B: Statistical Methodology. 1999;61:331–344. [Google Scholar]
- Damien P, Walker SG. Sampling truncated normal, Beta, and Gamma densities. Journal of Computational and Graphical Statistics. 2001;10:206–215. [Google Scholar]
- Daniels HE. The approximate distribution of serial correlation coefficients. Biometrika. 1956;43:169–185. [Google Scholar]
- Daniels MJ, Hogan JW. Missing data in longitudinal studies: Strategies for Bayesian modeling and sensitivity analysis. Chapman & Hall (CRC Press); 2008. [Google Scholar]
- Daniels M, Kass R. Nonconjugate Bayesian estimation of covariance matrices in hierarchical models. Journal of the American Statistical Association. 1999;94:1254–1263. [Google Scholar]
- Daniels MJ, Kass RE. Shrinkage estimators for covariance matrices. Biometrics. 2001;57:1173–1184. doi: 10.1111/j.0006-341x.2001.01173.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daniels M, Normand SL. Longitudinal profiling of health care units based on mixed multivariate patient outcomes. Biostatistics. 2006;7:1–15. doi: 10.1093/biostatistics/kxi036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daniels MJ, Pourahmadi M. Bayesian analysis of covariance matrices and dynamic models for longitudinal data. Biometrika. 2002;89:553–566. [Google Scholar]
- Davies PI, Higham NJ. Numerically stable generation of correlation matrices and their factors. BIT. 2000;40:640–651. [Google Scholar]
- Dégerine S, Lambert-Lacroix S. Partial autocorrelation function of a nonstationary time series. J Multivariate Analysis. 2003;89:135–147. [Google Scholar]
- Dempster AP. Covariance selection. Biometrics. 1972;28:157–175. [Google Scholar]
- Eaves D, Chang T. Priors for ordered conditional variances and vector partial correlation. J of Multivariate Analysis. 1992;41:43–55. [Google Scholar]
- Engle RF. Dynamic conditional correlation: A simple class of multivariate GARCH models. Journal of Business and Economics. 2002;20:339–350. [Google Scholar]
- Holmes RB. On random correlation matrices. SIAM J Matrix Anal Appl. 1991;12:239–272. [Google Scholar]
- Joe H. Generating random correlation matrices based on partial correlations. Journal of Multivariate Analysis. 2006;97:2177–2189. [Google Scholar]
- Jones MC. Randomly choosing parameters from the stationarity and invertibility region of autoregressive-moving average models. Applied Statistics. 1987;36:134–138. [Google Scholar]
- Jones RH. Maximum likelihood fitting of ARMA models to time series with missing observations. Technometrics. 1980;22:389–395. [Google Scholar]
- Kenward MG. A method for comparing profiles of repeated measurements. Biometrics. 1987;44:959–971. [Google Scholar]
- Kurowicka D, Cooke R. A parameterization of positive definite matrices in terms of partial correlation vines. Linear Algebra and its Applications. 2003;372:225–251. [Google Scholar]
- Kurowicka D, Cooke R. Completion problem with partial correlation vines. Linear Algebra and its Applications. 2006;418:188–200. [Google Scholar]
- Landau HJ. Maximum entropy and the moment problem. Bull of the Amer Math Soc. 1987;16:47–77. [Google Scholar]
- Liechty JC, Liechty MW, Muller P. Bayesian correlation estimation. Biometrika. 2004;91:1–14. [Google Scholar]
- Liu C. Comment on “The art of data augmentation” (Pkg: p1-111) Journal of Computational and Graphical Statistics. 2001;10:75–81. [Google Scholar]
- Liu X, Daniels MJ. A new algorithm for simulating a correlation matrix based on parameter expansion and reparameterization. Journal of Computational and Graphical Statistics. 2006;15:897–914. [Google Scholar]
- Liu X, Daniels MJ, Marcus B. Joint models for the association of longitudinal binary and continuous processes with application to a smoking cessation trial. Journal of the American Statistical Association. 2009 doi: 10.1198/016214508000000904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu N, Zimmerman DL. The likelihood ratio test for a separable covariance matrix. Statistics and Probability Letters. 2005;73:449–457. [Google Scholar]
- McCullagh P, Nelder JA. Generalized Linear Models. 2nd. London: Chapman & Hall; 1989. [Google Scholar]
- Pan J, MacKenzie G. On modelling mean-covariance structures in longitudinal studies. Biometrika. 2003;90:239–244. [Google Scholar]
- Pitt M, Chan D, Kohn R. Efficient Bayesian inference for Gaussian copula regression models. Biometrika. 2006;93:537–554. [Google Scholar]
- Pourahmadi M. Joint mean-covariance models with applications to longitudinal data: Unconstrained parameterisation. Biometrika. 1999;86:677–690. [Google Scholar]
- Pourahmadi M. Foundations of Time Series Analysis and Prediction Theory. Wiley; New York: 2001. [Google Scholar]
- Pourahmadi M. Cholesky decompositions and estimation of a covariance matrix: Orthogonality of variance-correlation parameters. Biometrika. 2007;94:1006–1013. [Google Scholar]
- Quenouille MH. Approximate tests of correlation in time series. Journal of Royal Statistical Society, Series B. 1949;11:68–84. [Google Scholar]
- Ramsey FL. Characterization of the partial autocorrelation function. Annals of Statistics. 1974;2:1296–1301. [Google Scholar]
- Stein ML, Chi Z, Welty LJ. Approximating likelihoods for large spatial data sets. Journal of Royal Statistical Society Series B. 2004;50:275–296. [Google Scholar]
- Wermuth N, Cox DR, Marchetti GM. Covariance chains. Bernoulli. 2006;12:841–862. [Google Scholar]
- Wong F, Carter CK, Kohn R. Efficient estimation of covariance selection models. Biometrika. 2003;90:809–830. [Google Scholar]
- Yang R, Berger JO. Estimation of a covariance matrix using the reference prior. Annals of Statistics. 1994;22:1195–1211. [Google Scholar]
- Yule GU. On the theory of correlation for any number of variables treated by a new system of notation. Roy Soc Proc. 1907;79:85–96. [Google Scholar]
- Zimmerman DL. Viewing the correlation structure of longitudinal data through a PRISM. The American Statistician. 2000;54:310–318. [Google Scholar]