Introduction

Since the beginning of satellite observations in 1979, Arctic sea ice coverage and volume in summer has decreased by approximately 50% and 70%, respectively, making it one of the most alarming signs of climate change1,2,3,4,5,6,7. To cope with the impacts of the shrinking area of sea ice, such as more freshwater storage, more frequent extreme weather events in the mid-latitudes, and changes to global shipping and trade passages8,9,10,11, adaptation and mitigation planning are based on credible projections of Arctic sea ice. Climate models collected in model inter-comparisons play a central role in formulating various management strategies. These strategies are based on probabilistic predictions about the outcomes of interest under different forcing scenarios, which are provided by simulations from carefully constructed model ensembles. However, models feature diverging projections of Arctic sea ice4,12,13,14,15,16,17,18, mainly because of model differences, such as different model responses to the same external forcing19. Some models might be biased in the same way when sharing portions of code, input datasets, or even the expertise of those developing the model, which could cause the multi-model mean to be biased low or high. To improve confidence in model projections and better inform decision-making, recalibrating the original results provided by model ensembles is therefore essential.

Phase 6 of the Coupled Model Inter-comparison Project (CMIP6) forms the basis of the Sixth Assessment Report (AR6) of the IPCC. The latest emissions and aerosol forcing, according to the Shared Socioeconomic Pathway (SSP) scenarios, are implemented in the climate models. CMIP6 models simulate a wider spread of mean sea ice extent in September than CMIP5 models20; however, a larger fraction of CMIP6 models reproduce the observed sensitivity of Arctic sea ice to anthropogenic CO2 emissions, leading to a multi-model ensemble mean sea ice sensitivity (defined as sea ice loss to a given amount of global warming) that is closer to observations21, and an earlier ice-free Arctic (defined as when Arctic sea ice extent falls below 1 × 106 km2). Therefore, the key question arises of whether an earlier ice-free Arctic projected by models is realistic. If so, management actions need to be adjusted in response to a more rapidly changing climate in the future. Much effort has been devoted to improving climate projections, such as evaluating, combining, and weighting models.

The emergent constraint method, which uses an ensemble of climate models to derive an inter-model relationship between a simulated but observable predictor in the models and a projected future change, has gained prominence in recent years and is a promising approach to reducing uncertainties in climate change projections18,22,23,24,25,26,27. For example, in a recent study that used two independent constraints to select models, the time for the first ice-free Arctic was projected to occur before 2040 under a medium emission scenario28. Another study established a simple model and constrained future sea ice using the mean state of present-day sea ice and local sea ice sensitivity, projecting that the ‘likely’ date for an ice-free Arctic will occur between 2040 and 2062 in September under a medium emission scenario, and between 2036 and 2056 under a high emission one29.

Detection methods applied to Arctic sea ice have revealed that the dynamics of the Arctic system have experienced substantial shifts since 199530. In this sense, constraining projection uncertainty by selecting models with good performance in sea-ice–related aspects (e.g., sea ice mean state, sea ice trends) during a certain time period (e.g., 1979 to the present, the most recent period), which many scientists have done2,13,21,27,28, might lead to unreasonable projections because the climate systems in the future may not be the same as those in the present. In addition, using an arbitrary calibration period to sub-select models to forecast the future is not a good way forward25, because the constrained results would somewhat depend on the subjective choice of the predictor31 and the length of the historical record32. Changes in the sea ice extent depend on how much more CO2 is being added to the atmosphere, or how much warming the earth will undergo33. In other words, it is the amount of remaining sea ice (depending on the model’s sensitivity to CO2 emissions) rather than the timing of an ice-free Arctic that we need to constrain. Thus, all of the aforementioned concerns suggest that using the same historical constraint for all projected time periods may lead to biases in the constrained results.

The unstable nature of climate systems has been generally neglected in previous studies, as well as IPCC assessment reports. One pioneering study showed how model weights change over time to achieve a satisfactory fit with the observations, which further supports the notion that using an arbitrary past representation does not mean the future is better constrained30. Taken together, subjective criteria may strongly affect the level of confidence in projections. In light of this, here we develop a time-variant emergent relationship between the simulated sea ice extent (SIE) state and projected SIE change that considers potential change in the climate system dynamics, thus providing a more reasonable projection of the future SIE. With this approach, the projected SIE over different periods during the 21st century under different emission scenarios is constrained by corresponding objective and optimal predictors. The results based on this approach provide information for policy makers as to how the Arctic environment will change in the future, as well as probabilistic projections of when an ice-free Arctic will likely occur under various emission scenarios. Further, it also provides us with a perspective for detecting tipping points in predictands based on the time-variant emergent constraints method.

Results

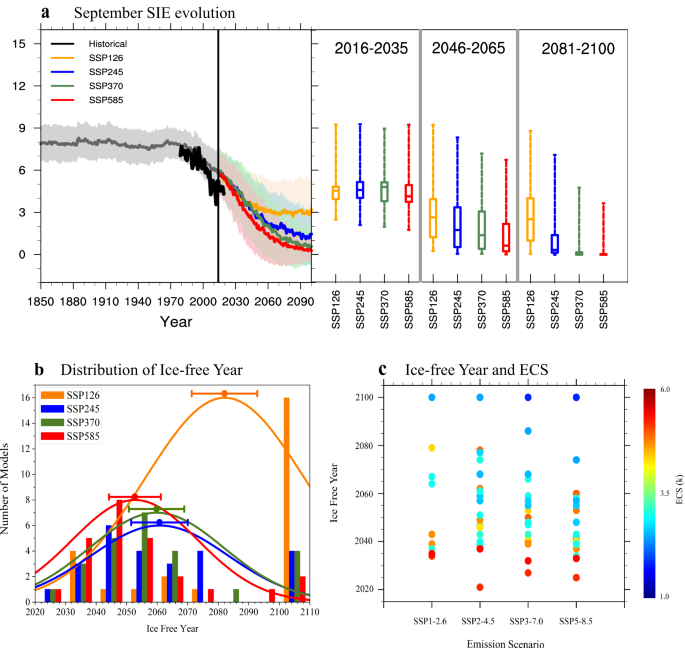
We begin by focusing on September Arctic SIE projections in CMIP6 models under four emission scenarios without applying emergent constraints (Fig. 1a). The September SIE (SSIE) continues to decrease from the 1970s to the end of the 21st century under all emission scenarios; however, 25 CMIP6 models have a wide spread in the simulated SSIE in both their historical simulations and under the four emission scenarios. The multi-model ensemble mean (MMEM; black line), which by definition represents the response to external forcing, matches well with the observations (green line) during 1979–2000. However, the MMEM shows a large divergence from the observed value after the year 2000, with the observations showing accelerating sea ice loss, but the MMEM still exhibiting a steady rate of sea ice melt. The failure of the MMEM to capture the observed change after 2000 might indicate that the dynamics of the climate system are changing, or that the model set should be recalibrated to bound the observed system behavior at present.

Fig. 1: Arctic SSIE change in observations and CMIP6 simulations.
figure 1

a SSIE in CMIP6 historical simulations (gray) and under the SSP1-2.6 (orange), SSP2-4.5 (blue), SSP3-7.0 (green), and SSP5-8.5 (red) scenarios from the MMEM (solid line) with one inter-model standard deviation (shading). The observations are shown as the black solid line. In the box-and-whisker plots, the band in the box represents the MMEM, the box represents the inter-quartile range (25th to 75th percentiles), and the ends of the whiskers represent the minimum and maximum simulation values. b Distribution of the first year in which the SSIE reaches the ice-free condition for all CMIP6 models under the four emission scenarios. c Projected ice-free year under four emission scenarios; the dots represent individual CMIP6 models, and colors represent the ECS values.

Full size image

The projected trajectories of the SSIE under the four different emission scenarios are difficult to distinguish at the beginning of the 21st century but start to diverge from the integration time. Under the SSP5-8.5 and SSP3-7.0 scenarios, the MMEM result projects that the Arctic will reach ice-free conditions by the 2060 s and 2070 s, respectively; however, under the SSP2-4.5 and SSSP1-2.6 scenarios (blue line), the MMEM of the SSIE remains above 1 km2 at the end of the 21st century, which indicates that without accounting for the modulation of internal variability on sea ice variation, the prescribed magnitude of greenhouse gas emissions could greatly influence the rate of sea ice melting. However, the uncertainty is large in the projected SSIE by CMIP6, especially before the 2060 s, with one standard deviation across the models of 2.2 × 106 km2 (1.9 × 106 km2) under the SSP2-4.5 (SSP5-8.5) emission scenario in the middle term (2046–2065), which directly results in the huge spread in the timing of an ice-free Arctic projected by the CMIP6 models (Fig. 1b). Under a high emission scenario (SSP5-8.5), raw CMIP6 ensemble estimates indicate that the Arctic will ‘likely’ (>66% probability) reach an ice-free state by September 2087.

Compared with CMIP5, the CMIP6 models as a whole project greater global surface air temperature warming over the 21st century21, which is caused mainly by higher equilibrium climate sensitivity (ECS) in response to increasing CO2 than in the case of CMIP532. In view of the proportional response of sea ice to cumulative CO2 emissions at long timescales34, we consider the extent to which the increased climate sensitivity in CMIP6 compared with CMIP5 affects the projected ice-free year. The inter-quartile range for an ice-free Arctic is 2051–2071 under SSP2-4.5 and 2044–2061 under SSP5-8.5, compared with 2045 to beyond 2100 and 2039–2055 in CMIP512,13. The breadth of this inter-quartile range is reduced by more than 64% under SSP2-4.5 from CMIP5 to CMIP6, possibly due to the higher ECS in CMIP6 models21.

Models that project an ice-free Arctic before 2040 are all high climate sensitivity models (Fig. 1c). Despite this relationship, the correlations between the ECS and projected SSIE under all emission scenarios are unstable and not robust during some time periods (Supplementary Fig. 1). This could be partially related to the complex relationship between the ECS and SSIE under transient climate change scenarios due to the evolving strength of climate feedbacks at different timescales and inter-model differences in SSIE internal variability.

Here, we propose to constrain the Arctic SSIE using the emergent constraint approach35,36. To confirm the robustness of the emergent constraint, we first provide a physical explanation for correlation between the two quantities37. The historical SSIE mean state is used in our study as the constraint for future SSIE in response to greenhouse gas emission during different periods. First, the sea ice change is proportional to cumulative CO2 emissions, and models with more sea ice loss in the past indicate that the feedback is stronger compared with those with slower sea ice loss. So as long as CO2 increases, this more intensive response to external forcing implies that more sea ice loss will continue in the future. In addition, the large spread in the projected SSIE during the 21st century by model sets from CMIP6 arises mainly from the biases in their simulated historical SSIE mean state29. Constraining future SSIE using past SSIE could reduce the projection uncertainty to the maximum extent. However, if the dynamics of the climate system are not, in fact, stationary, using the same historical constraint for different future periods might be unreasonable.

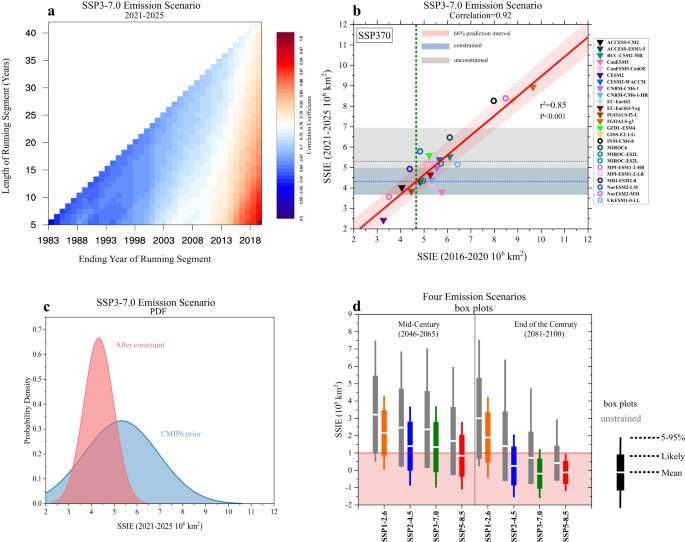
Considering potential changes in system dynamics, we propose a time-variant emergent constraint to better capture the evolving nature of sea ice. As an example, Fig. 2a shows that the highest inter-model correlation (correlation coefficient: 0.92) between the historical SSIE changes and the projected SSIE loss over 2021–2025 under the SSP3-7.0 emission scenario across 25 CMIP6 models occurs for the 2016–2020 period. This suggests that models retaining less sea ice over 2016–2020 are inclined to project less sea ice in the future. Based on this, we conclude that, compared with the observed SSIE over earlier periods on the same timescale or longer timescales, the SSIE mean state over the last five years could be the optimal constraint for future sea ice over the Arctic. The strong linear relationship between the simulated and projected SSIE, in combination with observations, provides an emergent constraint on the actual SSIE value during 2021–2025—that is, by using the regression to map from the observed SSIE during 2016–2020 (Fig. 2b). Our results show that the constrained SSIE of 4.32 × 106 km2 is 20% lower than that of the original CMIP6 ensemble mean (5.37 × 106 km2), with the uncertainty range reduced by 60% (Fig. 2c). A similar conclusion can be reached under the other three emission scenarios (Supplementary Fig. 3), except there are some differences in their optimal historical constraints (Supplementary Fig. 2).

Fig. 2: Emergent constraints on the projected 2021–2025 SSIE.
figure 2

a Inter-model correlations between the simulated SSIE changes over different periods and the projected SSIE changes (2021–2025) across 25 CMIP6 models under the SSP3-7.0 emission scenario. The black stars mark the historical periods that are most related to the projected SSIE changes. b Scatterplots of the mean state of SSIE during 2016–2020 versus the mean state of SSIE during 2021–2025 under the SSP3-7.0 emission scenario. The solid red line is the least-squares linear fit to the models and the pink shading indicates the prediction errors for the linear regression (66% confidence limit). The green vertical bar represents the average of three available observed values during 2016–2020 estimated from NASA Team, Bootstrap, and NSIDC-CDR. The constrained results are shown by the blue dashed line and the shading relates to the 66% confidence prediction interval. The gray dashed line represents the results derived from the original CMIP6 multi-model ensemble mean and the shading denotes the 66% confidence interval. c Probability density functions for the SSIE mean state during 2021–2025 before (blue) and after (red) the emergent constraints are applied. d constrained (colored) and original (gray) SSIE during the mid-century (years 2046–2065) and the end of the century (years 2081–2100) in four emission scenarios (SSP1-2.6, SSP2-4.5, SSP3-7.0, and SSP5-8.5) based on the CMIP6 ensemble.

Full size image

Repeating the same constraint procedure for projected SSIE during other time periods, we calculate the optimal historical constraints for 5-year sliding windows extending to the end of the 21st century for 25 CMIP6 models. It can be seen that under the SSP1-2.6 and SSP2-4.5 emission scenarios, the most useful constraints for future SSIE change little over time and are concentrated during 2016–2020 (Supplementary Fig. 4a, b). For SSP3-7.0 and SSP5-8.5, optimal constraints are relatively stable from 2025 to the mid-2050s but show substantial shifts beginning about 2054 and 2056, respectively. Emergent constraints can, to some extent, be treated as non-traditional model weighting, as the projections by models with smaller biases in the selected constraints will stay closer to the constrained changes. Therefore, the shift in historical constraints can be understood as a change in model weights, which suggests that the Arctic system is changing (Supplementary Fig. 4c, d). The scientific community is currently directing its attention to Earth system components that are believed to contain tipping points. The close proximity between the year of the shifts and the estimated optimal ice-free date, as indicated by the emergent constraint under SSP3-7.0 and SSP5-8.5 (Fig. 3a), suggests that utilizing this time-dependent emergent constraint could be a valuable approach for detecting future tipping points in the predictand. As discussed above, the optimal historical constraints for future SSIE change over time under the SSP3-7.0 and SSP5-8.5 emission scenarios, particularly after the mid-2050s, when the projected SSIE loss begins to slow down (Fig. 1a). It seems that using the same constraint for future SSIE under different emission scenarios and over different time periods, as previous studies have done, may actually be inappropriate. This is because the behavior of the system will change with varying intensities of external forcing, and the occurrence of tipping points will necessitate a change in predictors. Therefore, it should be noted that the optimal constraint for a certain period will not necessarily be a suitable constraint for another period.

Fig. 3: Constrained SSIE evolution and ice-free probability.
figure 3

a 5-year running mean SSIE evolution during 2025–2100 under four emission scenarios (SSP1-2.6, SSP2-4.5, SSP3-7.0, and SSP5-8.5) applied by emergent constraint. The colored solid lines show the best estimate of the linear fit and the corresponding shading denotes the 66% confidence prediction interval. The horizontal solid black line represents the threshold for the ice-free state. b cumulative probability density function for the year when the Arctic will reach the ice-free state in September under different emission scenarios (SSP1-2.6, SSP2-4.5, SSP3-7.0, and SSP5-8.5).

Full size image

We then use these changing historical constraints over time to constrain the SSIE in the future. Strong inter-model correlations exist during all periods under different emission scenarios, confirming the usefulness of these selected constraints (Supplementary Fig. 5). The constrained mean values of SSIE during the middle and end of the century are all much lower than the unconstrained CMIP6 mean results under all emission scenarios (Fig. 2d), indicating that an ice-free Arctic will occur earlier than originally estimated from climate models. The observationally constrained likely ranges for the future SSIE under the SSP3-7.0 and SSP5-8.5 emission scenarios are all below 1 × 106 km2, suggesting that the Arctic will ‘likely’ (>66% probability) be ice-free in these scenarios. The likely ranges for an ice-free Arctic are reduced from the period of 2039 to beyond 2100 to the period of 2041–2071, and from the period of 2044 to beyond 2100 to the period of 2037–2066 under the SSP3-7.0 and SSP5-8.5 scenarios, respectively (Fig. 3a). This constraint advances the ‘likely’ date of an ice-free Arctic by 27 years from 2087 to 2060 under the high emission scenario (SSP5-8.5). For the medium and low emission scenarios, an ice-free Arctic will likely occur by 2080 and beyond 2100, respectively (Fig. 3b).

To compare with the results derived using the traditional emergent constraint (i.e., using the same predictor to continuously constrain the future predictand over different periods), we adopt a certain range of predictor choices. Two constraints are produced based on the SSIE during (a) 2016–2020 and (b) 2007–2011. We choose these two periods because 2016–2020 is the period closest to the future climate, and 2007–2011 has previously been used in CMIP5 models to constrain SSIE projection13. It can be seen that, compared with the results estimated by the constant constraint, our time-variant constrained method brings the ice-free date forward by around 5 ~ 10 years under SSP3-7.0 and SSP5-8.5 (Supplementary Fig. 6), suggesting that the Arctic is changing faster than previously conceived, and more efficient mitigation measures should be adopted as soon as possible to avoid a permanent ice-free Arctic.

Discussion

Here, we propose a time-variant emergent constraint method for future SSIE, which considers potential change in climate system dynamics and provides an approach for detecting tipping points in the future climate system. Observationally constrained future SSIE in the SSP5-8.5 scenario by mid-century (2046–2065) is estimated at −0.37 to 2.03 × 106 km2 (17–83%), and by the end of the century (2081–2100) at −0.53 to 0.78 × 106 km2. The constrained mean SSIE is 47% lower by mid-century than the unconstrained warming simulated by the CMIP6 ensemble. The observational constraint identified in this study adds another line of evidence that an ice-free Arctic before 2030 projected by high ECS from some of the latest CMIP6 climate models is unlikely. We provide an estimate of the observationally constrained likely range for the ice-free date based on CMIP6 models from 2037 to 2066 (17% to 83% range) under the high emission scenario. Our time-variant constrained results bring the ice-free date forward by around 5 ~ 10 years under SSP3-7.0 and SSP5-8.5 compared with traditionally constrained methods.

The emergent constraint method, as mentioned above, assumes that the relationship between the present and future climate metrics in climate models also holds true in reality. However, it is theoretically possible that this relationship is an artifact of the climate models if some crucial processes leading to the nonlinear reduction of sea ice are missing in the models but are present in reality. These missing processes would compromise the emergent relationship and potentially bias the constrained estimate. However, it would be an extreme situation for all models to be wrong; in most instances, each model is wrong in a different way, and the inter-model spread can adequately reflect the influence of different physical parameterizations on sea ice variation. Therefore, the models can collectively generate useful and nearly perfect future predictions when combined with observations.

However, although scientists have made considerable efforts to narrow the spread of sea ice projections among the CMIP models, the predicted time interval for an ice-free Arctic remains large. The presence of internal variability can sometimes overwhelm a forced signal on decadal timescales and regulate the occurrence of an ice-free Arctic by around two decades15,16,21,38,39,40. In addition, the effect of internal variability on the SSIE will increase as the sea ice retreats41, although the relevant physical mechanism is not yet well understood. Further exploration of the physical processes responsible for the decadal variability of the SSIE will effectively improve our ability to provide a more precise estimate for the timing of a future ice-free Arctic.

Methods

Observational data

Observed sea ice data are provided by the National Snow and Ice Data Center (NSIDC). We use several different sea ice concentration (SIC) observational records obtained with different algorithms to take observational uncertainty into account: (i) Bootstrap42; (ii) NASA Team43; and (iii) a synthesis of (i) and (ii) [the NOAA/NSIDC climate data record CDR)44].

The Arctic sea ice extent is defined as the total area of grid cells with SIC > 15%. The timing of an ice-free Arctic is defined as when Arctic sea ice extent falls below 1 × 106 km2 for 5 consecutive years, because sea ice will persist along the northern coastlines of Canada, Alaska, and Greenland for a long time.

Model simulations

We use monthly mean sea ice concentration (SIC) data from 25 CMIP6 models (Table S1). The models were selected according to the availability of variables and scenarios required for our study. We analyzed the simulations from the all-forcing historical experiments (1850–2014) and projections (2015–2100) under four scenarios, SSP1-2.6, SSP2-4.5, SSP3-7.0, and SSP5-8.5, which are a combination of the Shared Socioeconomic Pathways (SSPs)45 and the forcing levels of the RCPs. The different ensemble members for each model are averaged to avoid weighting toward any model that provides more simulations and to eliminate random errors. The SIE is calculated using the native grid of each model. The likely (17–83%) ranges of the CMIP6 projections are derived by ordering projections from the individual models first, and then linearly interpolating the calculated percentiles. To illustrate SSIE change with cumulative carbon dioxide emissions, the future climate is divided into three specific 20-year periods: 2016–2035 (near-term), 2046–2065 (mid-term), and 2081–2100 (long-term). The effective climate sensitivity (ECS) of the climate models is estimated based on the following equation:

$${ECS}=-{F}_{2x}\gamma$$
(1)

where F2x is the radiative forcing due to doubling of CO2 and \(\gamma\) represents the radiative feedback parameter, which is negative in a stable system. Following previous research46, we regress the top-of-atmosphere (TOA) net downwelling radiative flux anomalies against the annual mean global surface temperature change in a CO2-only simulation in which atmospheric CO2 concentration is quadrupled to estimate the ECS. The estimate is divided by 2 to represent the ECS with respect to CO2 doubling.

Observational constraint on future projections

We relate the diagnostics of the climate model projections to the present-day climate. Let Y = \({\left\{{y}_{1},{y}_{2},\ldots ,{y}_{n}\right\}}^{T}\) be the vector of the projected model values to be corrected (here, the projected SSIE), in which n is the number of models. Then we suppose that there is a linear relationship between the historical simulated diagnostic X (here, the simulated SSIE) and the projected model value Y (here, the projected SSIE), which can be written as:

$${\bf{Y}}={\bf{1}}\,{\beta }_{0}+{\bf{X}}\beta +\varepsilon ,$$
(2)

where 1=\({\left\{\mathrm{1,1},\ldots 1\right\}}^{T}\) is a column vector of size n; X=\({\left\{{x}_{1},{x}_{2,\ldots ,}{x}_{n}\right\}}^{T}\). The vector \(\varepsilon\) represents the uncertainty in the projections, which can be understood as all the factors related to the projections of Y not included in X and the nonlinear interactions between the diagnostic X and the projected model value Y; \({\beta }_{0}\) and \(\beta\) are the regression model parameters to be calculated. The model parameters \({\beta }_{0}\) and \(\beta\) can be estimated by a least squares fit:

$$\hat{{\beta }_{0}}={\left({{\boldsymbol{1}}}^{{\rm{T}}}{\boldsymbol{1}}\right)}^{-1}\left({{\boldsymbol{1}}}^{{\rm{T}}}{\bf{Y}}-{1}^{{\rm{T}}}{\bf{X}}{\rm{\beta }}\right)\equiv {{\bf{N}}}^{{\rm{T}}}{\bf{Y}}-{{\bf{N}}}^{{\rm{T}}}{\bf{X}}{\rm{\beta }},$$
(3)

where N \(\equiv {({{\bf{1}}}^{{\rm{T}}}{\bf{1}})}^{-1}{\bf{1}}\). Next, we assume that the linear relationship between the simulated and projected values in Eq. 2 holds true in the real climate. Under this assumption, Eq. 2 can be used to adjust the original projections of Y to \({y}_{0}\) using the vector of the observed diagnostic \({X}_{0}:\)

$$\,\,\hat{{{\bf{y}}}_{{\bf{0}}}}=\hat{{\beta }_{0}}+{{\bf{X}}}_{{\bf{0}}}^{{\bf{T}}}\hat{\beta }=\left[{{\bf{N}}}^{{\bf{T}}}+\left({{\bf{X}}}_{{\bf{0}}}^{{\bf{T}}}-{{\bf{N}}}^{{\bf{T}}}{\bf{X}}\right){\left({{\bf{X}}}^{{\bf{T}}}{\bf{X}}-{{\bf{X}}}^{{\bf{T}}}{\bf{1}}{{\bf{N}}}^{{\bf{T}}}{\bf{X}}\right)}^{-{\bf{1}}}\times ({{\bf{X}}}^{{\bf{T}}}-{{\bf{X}}}^{{\bf{T}}}{\bf{1}}{{\bf{N}}}^{{\bf{T}}})\right]{\bf{Y}},$$
(4)

where \(\hat{{{\bf{y}}}_{{\bf{0}}}}\) is the estimate of \({{\bf{y}}}_{{\bf{0}}}\), and the prediction error of the regression at the value of x = xo can be written as:

$$\sigma =\sqrt{{S}^{2}[1+\frac{1}{n}+\frac{{({{\bf{X}}}_{{\bf{o}}}-\bar{X})}^{2}}{{S}_{{xx}}}]},$$
(5)

where S2 = \(=\frac{({\bf{Y}}-\hat{{\bf{Y}}}){({\bf{Y}}-\hat{{\bf{Y}}})}^{{\bf{T}}}}{n-2}\) and \({S}_{{xx}}=({\bf{X}}-\bar{{\bf{X}}})({\bf{X}}-\bar{{\bf{X}}})\)T.

Following previously established methods47,48, for a linear regression, based on the assumption that the error of regression is normally distributed, the Gaussian probability density function of y given xo is expressed as:

$$P{\{y{\rm{|}}x}_{0})=\frac{1}{\sqrt{2\pi {\sigma }^{2}}}\exp \left\{-\frac{{({\bf{y}}{\boldsymbol{-}}{\hat{{\bf{y}}}}_{{\bf{0}}{\boldsymbol{)}}}}^{2}}{2{\sigma }^{2}}\right\}$$
(6)