Preprint
Article
Landslide Susceptibility Assessment Modeling in Yunnan Plateau Lake watershed: A Case Study for Dianchi Lake Watershed
Altmetrics
Downloads
106
Views
29
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Abstract
The nine plateau lake watersheds in Yunnan are important ecological security barriers for southwest China, and the prevention and control of landslides are important considerations in the management of these watersheds. Taking Dianchi Lake watershed as a typical study area, this paper puts forward an improved comprehensive process of landslide susceptibility evalua-tion, and discusses the model’s sensitivity regarding susceptibility to landslides. The compre-hensive process is based on the weight of evidence method (WoE) and integrates many analyti-cal techniques, such as cross-validation, multi-quantile cumulative Student’s comprehensive weight analysis, independence tests, step-by-step modeling, ROC analysis and ROC-based sus-ceptibility zoning. This paper established fourteen models, with high accuracy and validity AUC, reaching 0.83-0.87 and 0.85-0.88, respectively. Moreover, according to the susceptibility zoning map compiled using the optimal model, 80% of landslides can be predicted in the very high and high susceptibility zones, which only account for 19.58% of the study area. Finally, the strategies for geological disaster prevention and ecological restoration deployment were put forward, providing great guiding significance for deeply understanding the landslide susceptibility of lake watersheds (Dianchi Lake) in Yunnan Plateau and guiding the planning and deployment of landslide prevention and mitigation activities and ecological restoration in the watershed.
Keywords:
Subject: Environmental and Earth Sciences - Geophysics and Geology
1. Introduction
Yunnan province is an important ecological security barrier in southwest China, and lakes are important ecological areas. The government of Yunnan province is promoting the ecological protection and restoration of nine plateau lake watersheds (Figure 1), and landslide disaster prevention is one of the important goals of these activities. In order to support this ongoing project, it is necessary to evaluate landslide susceptibility, taking lake watershed as the unit, establish the geological environment and human activity factors that may affect or control landslide susceptibility in the watershed, understand the distribution of landslide susceptibility in the watershed, and guide the formulation of targeted prevention and control countermeasures. Dianchi Lake is the largest of the nine plateau lakes in Yunnan, and Kunming city is in this watershed, where human engineering activities are relatively strong, and so it is reasonable to choose Dianchi Lake watershed as the research area.
Landslides in plateau mountainous areas are always a problem, because they affect people's lives, destroy the land surface and cause economic losses [1]. Identifying the dangerous areas related to landslides is an important part of disaster management [2], and it is also an important basis for promoting human safety, infrastructure development and ecological environment protection in these mountainous areas [1]. Landslide susceptibility analysis (LSA) describes the spatial probability of landslides [3,4]. On the regional scale, the modeling method of landslide susceptibility based on statistics is considered appropriate [2,5,6,7]. We used the Weight of Evidence (WoE) method [8] to complete this analysis, which is a statistical-based method and also represents an intermediate and complex data-driven method [9]. Although WoE is a bivariate statistical method frequently used in LSA in recent decades [1,2,6,7,9,10,11,12,13,14,15,16], establishing how to optimize the modeling process to improve the accuracy and validation of the model is a problem worth exploring. In addition, because WoE only uses discrete data, continuous raster data need to be classified, but there is no standardized method of factor data classification, which is another problem worth exploring [2,4,8].
This study focuses on LSA and landslide susceptibility mapping (LSM) in the Dianchi Lake watershed of Yunnan Plateau, which has important ecological barrier significance. This method has outstanding application value, aiming at strengthening the ability to assess the susceptibility risk of landslide disasters and improving the corresponding consulting services for stakeholders related to disaster reduction. In terms of research content, on the one hand, the characteristics of sensitive factors of landslide susceptibility were clarified; on the other hand, the spatial distribution of landslide susceptibility was clarified, which provides important technical support for guiding ecological restoration and geological disaster prevention and mitigation deployment in plateau lake watersheds. In terms of technology, this paper puts forward an improved comprehensive process of landslide susceptibility evaluation based on the WoE method, including: (1) data preparation; (2) optimizing the compilation of datasets for factor classification based on cumulative Student’s comprehensive weight (sC) curve and WoE statistics; (3) screening modeling factors based on the cross-validation theory and AUC factor indicators; (4) step-by-step modeling to optimize high-performance models; and (5) dividing landslide susceptibility zones base on ROC. In this paper, the improved analysis process was applied to obtain the results of the WoE landslide susceptibility model with excellent fitting performance and prediction performance (both AUC reached 0.87), and the spatial distribution map of landslide susceptibility classification in the study area was compiled, and the strategies of geological disaster prevention and ecological restoration deployment were put forward, which is of great guiding significance for deeply understanding the landslide susceptibility of lake watersheds (Dianchi Lake) in Yunnan Plateau and guiding the planning and deployment of landslide prevention and mitigation and ecological restoration in the watershed.
2. Study Area and Data
2.1. Study Area
The study area is bounded by the watershed of Dianchi Lake watershed (Figure 1), with an area of 2906.44km2. The water surface of Dianchi Lake and reservoir, the center of Kunming basin, the sub-basins and some flat hilltops are not prone to landslides. Therefore, based on the landform results of DEM classification [17,18], deducting 700.15km2 of the "flat" category, the actual analysis area in this paper was 2206.29km2. This area is a lake basin and mountainous terrain in the middle of Yunnan Plateau, with Dianchi Lake’s waters and basins in the south-central part, rugged mountains in the north, east and south, and Xishan mountain in the west, with steep fault cliffs. The elevation of this area ranges from 1896m at the surface of Dianchi Lake to about 2800m in the mountainous area, with a height difference of more than 900m. The steep mountain terrain around the basin, the continuous and rapid cutting of rivers, the heavy rainfall in the rainy season and the man-made influence caused by the downward cutting of slopes during road construction make the area prone to slope failure.
2.2. Landslides Dates and Data Preparation Based on Random Sampling
The study area has a good working history in landslide survey, and it is the key monitoring and prevention area of landslides in Yunnan Province. Through field investigation, the list of historical landslides was checked and revised, and a total number of 228 landslides were included in the list of landslides analyzed in this paper (Figure 1).
We adopted the cross-validation technique, the basic technique used to evaluate the uncertainty of statistics and models by using test datasets that do not involve model training [4,20,21], to prepare the data. Figure 2 briefly summarizes the compilation process of the landslide dataset: (1) we divide all landslide data (ALL) into a training dataset (TRN) containing 158 landslides and a test dataset (TST) containing 70 landslides by using random sampling tools, and TRN and TST were not duplicated. The former and the latter corresponded to about 70% and 30% of ALL, respectively. TRN was used to calibrate the model and TST was used to evaluate the performance of the model. (2) In order to estimate the model variables that depend on the sample size, we used the random sampling tool to generate 100 random sub-samples with TST size from TRN, and some landslides in different random sub-samples were allowed to be repeated, forming a training data subset trn.
2.3. Factor Data
According to the characteristics of the study area, data availability and previous studies, the landslide control factors can be roughly divided into different groups [6,15]; the compiled landslide control factors are listed in Table 1. At first, we did not rule out the available or main factors that are easy to deduce, because these factors may help to explain the landslide susceptibility in the study area. These factors have been used in other studies, and descriptions of these factors can be found in a large number of studies [2,15,22,23,24,25,26], so this article did not elaborate upon this further. Because landslides usually do not happen by accident, they are unevenly distributed in different factors and factor classifications [2,27]; we thus used the method in Section 3.3 to statistically evaluate the relationship between landslide occurrence and spatial distribution of some factors based on single-factor WoE statistics.
3. Methods
3.1. Weights-of-Evidence Method (WoE)
The WoE method is a well-known and widely used bivariate statistical method which is used to estimate the relationship between observation data (landslide training inventory) and potential control factors (geological and geomorphological factors) [8,39]. A single factor’s weight is superimposed on the linear model to obtain the overall landslide susceptibility model [1,8,11,39]. It was first introduced in the late 1980s for the application of GIS-based geological science, mainly to assist the mapping of mineral potential [8,39,40,41,42]. Later, this method was widely used in LSM [1,2,6,7,10,11,12,13,14,15,16].
is defined as the unit with geological disasters, is defined as the unit without geological disasters, is defined as the unit in the evidence factor area, is defined as the unit outside the evidence factor area, is defined as the conditional probability symbol, and is defined as the number of grid pixels. WofE considers two weights and posterior probability[2,6,8,15,39,41,42]:
The weight symbols and do not represent the mathematical meaning of numerical values, but rather represent the presence (positive) and absence (negative) of feature classes in a given raster cell. According to the above formula, a positive logic value indicates the positive influence of a given variable, a negative logic value indicates the negative influence, and a logic value of zero indicates no influence.
The posterior probability is an indicator of susceptibility, with a higher value indicating higher susceptibility, and a lower value indicating lower susceptibility. The formula for calculating the posterior probability is: , , , where: is “+” when the -th evidence factor layer exists, an is “-“ when it does not exist; is the weight of the existence or non-existence of the -th evidence factor.
In order to evaluate the spatial correlation strength between single factors and landslide and the performance of the model, this paper used the receiver operating characteristic curve (ROC) algorithm, which is a technique to visualize and evaluate the classifier performance by describing the ratio of the true positive rate (sensitivity) to false positive rate (1-specificity) [43]. The area under the ROC curve (AUC) provides a quantitative index to compare the advantages and disadvantages.
3.2. Main Analysis Process
In this paper, an improved evaluation process of landslide susceptibility based on WoE is proposed, which mainly includes: (1) data preparation, (2) optimizing the compilation of datasets for factor classification, (3) screening modeling factors, (4) gradually adding factor modeling to optimize high-performance models, and (5) dividing landslide susceptibility level zones.
(1) Data preparation. Clean up the landslide inventory, and compile the training set (TRN), test set (TST) and training set subset (trn) by using cross-validation technology (see Section 2.2 for details). Prepare the initial dataset of factors (see Section 2.3 for details).
(2) Optimizing the compilation of datasets for factor classification. In this paper, a sub-process of optimizing factor classification is proposed to process the initial dataset of factors to obtain excellent classification dataset. See Section 3.4 for the introduction of this method.
(3) Screening modeling factors. Firstly, according to the single factor WoE statistical results, the factors of low AUCs (this paper chooses AUC < 0.59) are excluded. Secondly, exclude the factors with high correlation. The use of strongly correlated datasets may lead to incorrect estimation of factor contribution and expansion of estimated probability value [44]. Chi-square-based contingency analysis is performed on the classified data based on the raster [4,15], according to Pearson's C and Cramer's V, to measure the correlation between discrete datasets.
(4) Step-by-step modeling, and optimizing the high-performance model. According to AUCs and correlation statistical indicators obtained using single-factor WoE statistics, the factors are sorted and combined. The model is based on the factor composition with high AUCs. Then, try to add follow-up factors into the new model in turn, and recalculate and evaluate the ROC_M curve and AUC_M index of the new model. Evaluate the fitting performance and uncertainty of the model. The range and average ROC curves (ROC_M_trn2trn) and AUC (AUC_M_trn2trn) of 100 sensitivity model results are obtained by fitting trn with the model based on the average weight calculated by trn. After this, evaluate the prediction performance of the model. The ROC curve (ROC_M_trn2TST) and AUC (AUC_M_trn2TST) are obtained by fitting TST with the model based on the average weight calculated by trn. Use the above ROC_M and AUC_M indicators to evaluate whether and how the model benefits from the last added factor, and discard the factors that cannot improve the AUC_M indicators of the model or improve the ROC_M consistency.
Figure 3.
Flow chart of the improved WoE landslide susceptibility assessment.
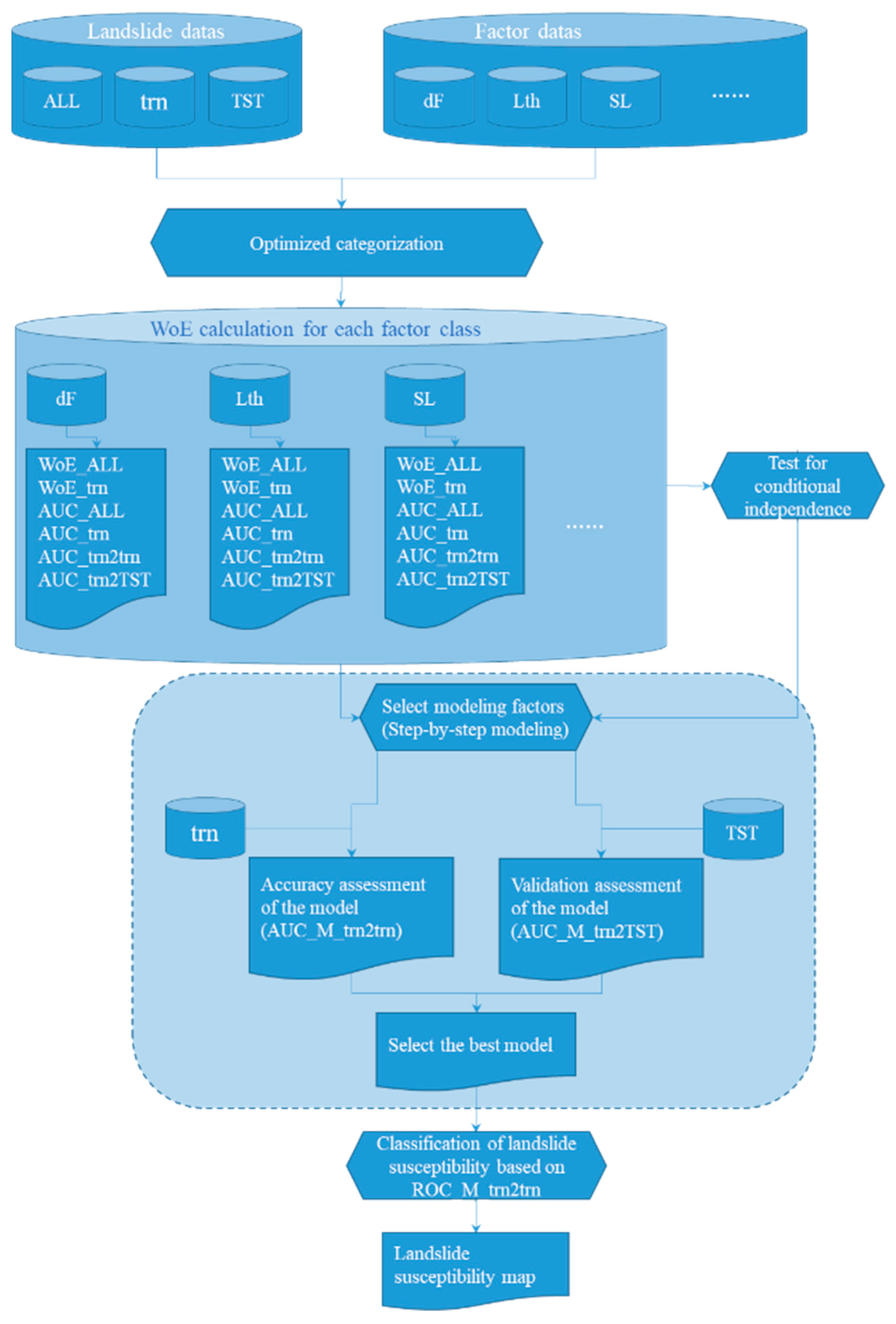
(5) Landslide susceptibility zoning based on ROC_M. Adopt a zoning method to improve the readability of the landslide susceptibility map. This method uses the success rate to describe that the cumulative landslide area exceeds the cumulative area that is considered vulnerable [45]. In the ROC curve, the Y-axis representing the true positive rate corresponds to the cumulative landslide area, and the X-axis representing the false positive rate describes the cumulative research area without landslide area, which is regarded as an area that is susceptible but does not include landslide area, and is an approximation of the total research area. There is no established standard for the definition of the partition threshold. In this paper, we used 50% of all landslide pixels to represent very-high-susceptibility areas (VHS), which means that an aggregated susceptible area contains 50% of the detected landslide areas. Assuming that the location of future events will follow the drawn susceptibility model, we can also assume that about 50% of all future landslide areas will also be located in this area. We used values of 30% for high-susceptibility areas (HS), 15% for medium-susceptibility areas (MS), 4% for low-susceptibility areas (LS), and about 1% for very-low-susceptibility areas (VLS). Therefore, the first two areas (VHS and HS) include about 80% of the known landslide areas.
3.3. WoE Statistic Process
Using cross-validation technology, with single-factor classification data, ALL, trn and TST, according to the WoE method, the regional distribution of discrete class factors, the corresponding landslide pixel frequency, weight, variance, ROC and AUC in these classes are counted. The output data include ten items: WoE_ALL, sC_ALL, WoE_trn, sC_trn, AUC_ALL, AUC_trn, ROC_trn2trn, AUC_trn2trn, ROC_trn2TST, and AUC_trn2TST, where WoE_ALL, sC_ALL and AUC_ALL are the weight, sC and AUC calculated based on ALL, respectively; WoE_trn, sC_trn, and AUC_trn are the mean weight, sC and AUC calculated 100 times based on trn, respectively; ROC_trn2trn and AUC_trn2trn are the single-factor accuracy assessment indexes modeled by single-factor weight WoE_trn and fit to trn; and ROC_trn2TST and AUC_trn2TST are the single-factor validity assessment indexes modeled by single-factor weight WoE_trn and fit to TST.
Figure 4.
Process flow chart of single factor WoE statistic.
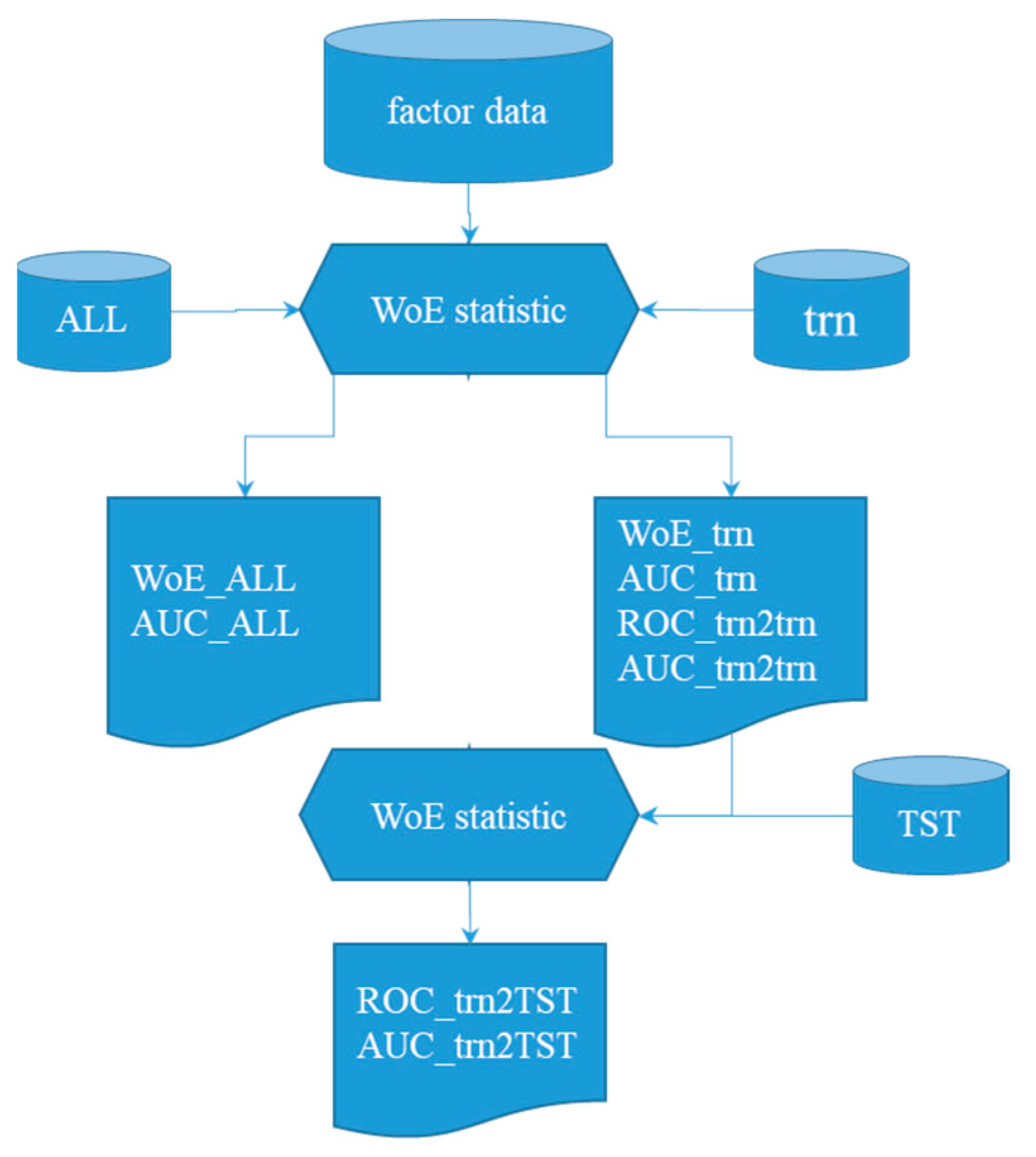
Because landslides usually do not happen by accident [4,6,27], one can statistically evaluate the relationship between landslides and the spatial occurrence of some parameters based on the above single-factor WoE statistics. In this paper, trn (containing 100 subsets) was used for statistics, and the statistical process was repeated 100 times for each control factor. Calculate the mean weight of each factor category (WoE_trn) and its corresponding statistical values, such as variance and standard deviation. ROC is used to graphically evaluate the classification ability of each factor for each statistic. This statistical process has two advantages [6]. Firstly, based on its estimated variance, it can better represent the general uncertainty of the sensitivity model; Secondly, for classified data, it can be determined whether the significant weight has accidental characteristics or whether it can be reproduced from different random samples, which is more likely to be causal.
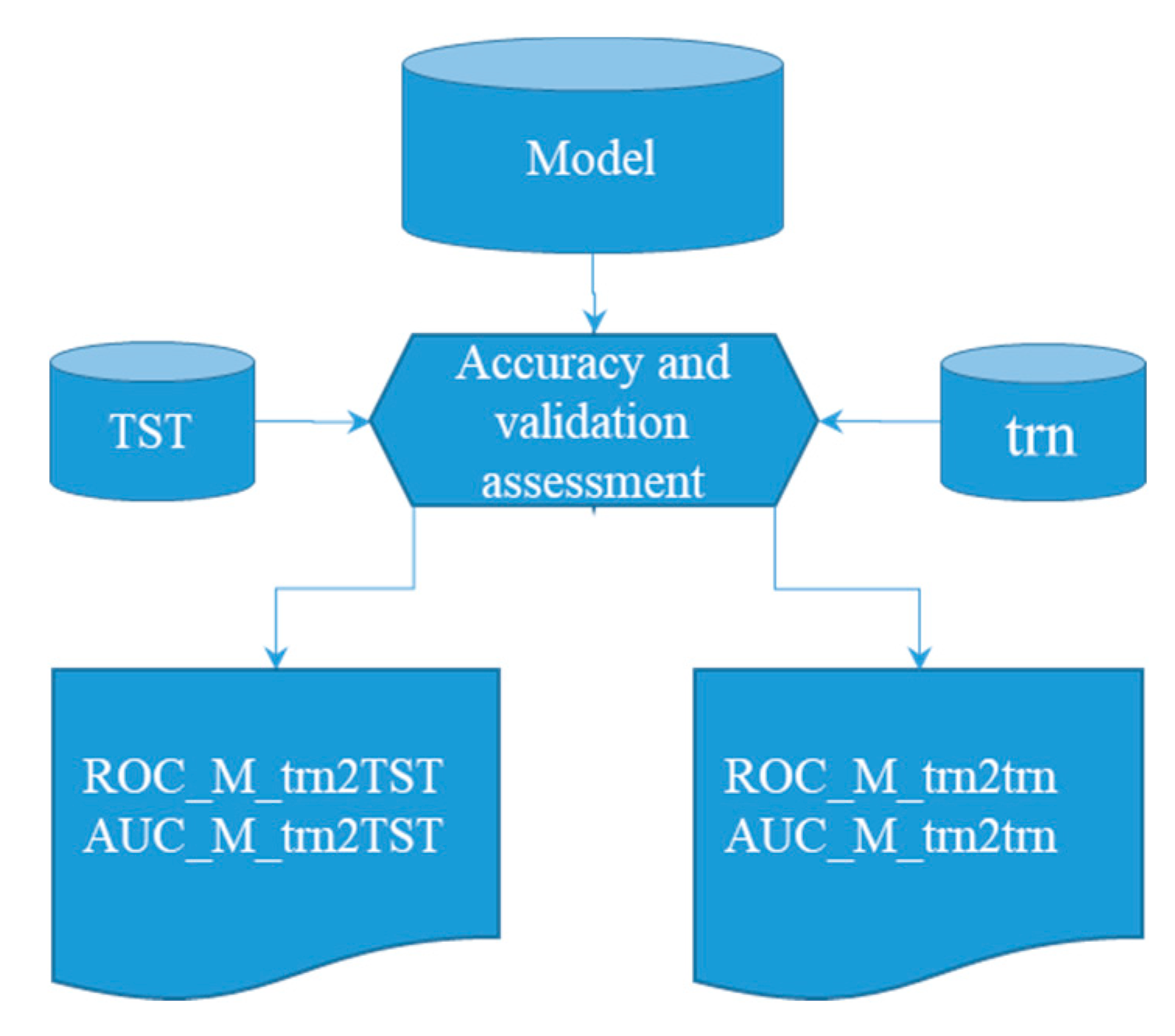
Use trn to evaluate the accuracy performance of the model and use TST to evaluate the validation performance of the model for new data prediction [7,16]. If the ROC curve based on TST falls within the ROC curve range based on trn (representing MSE), it shows that the accuracy and validation of the model can be good; if not, the model may be over-fitted.
Figure 5.
Process flow chart of accuracy and validation assessment of models.
3.4. Optimization Process of Single Factor Classification
Because WoE uses discrete data, it is necessary to classify continuous single factor data discretely, which will lead to the discontinuity of factor weights. The traditional single-factor discrete classification number and classification threshold determination is subjective. In this paper, a single factor classification optimization process (Figure 6) is proposed, and the main steps are as follows:
Firstly, generate the cumulative sC curve. This method involves subdividing the continuous numerical single-factor raster into classes according to the quantile and calculating its weight and corresponding variance for each class. The difference between the two weights—that is, the comprehensive weight—the quantitative evidence factor and the correlation between geological disasters are calculated as follows [39]: . If is positive, the evidence factor is favorable to geological disasters, while if it is negative, it is unfavorable to landslides. If is close to zero, it shows that the evidence factor has little to do with geological disasters. A confidence measure defined by contrast divided by its standard deviation is introduced, which is similar to Student’s comprehensive weight sC. The sC is relatively large when the standard deviation is small, so the results are more reliable. When the test values of sC are 1.96 and 2.326, the confidence is 97.5% and 99% [8,39,41]. , , , where 、 and are standard deviations of , and , respectively. Use the accumulated sC to define a new discrete distance category [6]. As long as the weight value is positive, the sC should be increased; when the weight value is close to zero, it should be flattened; and when the weight value is negative, it should be reduced. Therefore, the shape of the cumulative sC curve is expected to show its maximum value at the position of its maximum expected influence. If there is more than one maximum, it indicates the distortion effect of another variable [6].
In this step, we put forward an improved technical subprocess: using the results of multiple quantile calculations for comprehensive analysis—that is, compiling a series of cumulative sC curves of quantile statistics at the same time. This will help to show the changing trend of cumulative sC more comprehensively and capture the possible segmentation threshold. First, it can guide the selection of segmentation threshold and reduce the subjectivity of segmentation threshold setting. Secondly, it can reveal the sensitivity of factor values to landslides in a single-factor segment, and also maintain the continuity of the weight trend well, and improve the discrimination of landslide sensitivity of each influencing factor.
Set the threshold of classification and segmentation based on the cumulative sC curve, re-classify the factors, and perform single factor WoE statistics on the re-classified factor data (Section 3.3).
Then, set a new trial segmentation threshold and repeat the above steps.
Finally, we propose determining the best classification based on two criteria (Criterion 1 and Criterion 2). Criterion 1: Division or merger, is it beneficial to (1) eliminate classifications of continuous sC<2; (2) reduce classifications of sC<2; (3) increase classifications of sC>2; or (4) increase the value of AUCs? After several rounds of trial calculation, the optimal classification is determined according to Criterion 2: Select the best categorization with (1) the highest AUCs; (2) better fitting between ROC_trn2TST and ROC_trn2trn; and (3) more classes with sC>2.
4. Results
4.1. Cumulative sC Statistical Curve of Continuous Single Factor
In this study, the landslide dataset ALL was used to count the continuous numerical factors by using the statistical method proposed in Section 3.4. In order to obtain the statistical curves after classification with different quantiles, we draw the frequency distribution of the original data of factors and the cumulative sC statistical curves of six quantiles of 100, 80, 60, 40, 20 and 10 (Figure 7), which reveals the correlation between continuous numerical factors and the spatial distribution of landslides in different quantiles in detail, not only reflecting the changing trend of cumulative sC, but also showing the details of the changes in cumulative sC. These cumulative sC curves are a reference to guide the selection of classification thresholds. In this study, after several rounds of trial calculation, we summarized the following experiences in setting classification thresholds: (1) at the maximum peak and minimum valley, (2) more classification thresholds can be set for curves with steep slopes, (3) the secondary peak (valley) values of curves drawn using different quantiles can be tested as classification thresholds, but only the peak (valley) values of curves drawn using individual quantiles should be selected as classification thresholds. (4) The more classification items with sC>2, the better. (5) The fewer the total classification items in the classification results, the better. (6) The larger the three AUCs (AUC_ALL, AUC_trn and AUC_TST), the better. (7) ROC_trn and ROC_TST should be coordinated (ROC_TST is within the range of ROC_trn).
4.2. Results of Single Factor WoE Analysis
After implementing the technical processes in Section 3.4 and 3.3, we obtained the evidence weight and sensitivity strength analysis results of each factor (Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19 and Figure 20). The results are shown in eight pictures. In the first line, the first picture presents the statistics of the number of grids in each category of factors; The second picture shows the distribution of all landslide data in each factor classification; The third picture is a C histogram of factor classification based on all landslide data statistics, and the black vertical line is the error bar of C; and the fourth picture presents the ROC_ALL and AUC_ALL based on all landslide data statistics. In the second line, the first picture is a violin-box diagram based on 100 subsets of trn and counting the distribution of landslide data 100 times in each factor classification; the second picture is a C violin-box diagram of factor classification based on 100 subsets of trn; and the third picture presents the ROC and AUC, which have been counted 100 times based on 100 subsets of trn. The fourth figure is a statistical chart of fitting performance and prediction performance of the single-factor WoE model based on 100 subsets of trn, where the blue line is the mean ROC (ROC_trn2trn) of the model's fitting performance to 100 subsets of trn, the gray band is the ROC range of the model's fitting performance to 100 subsets of trn, and the orange line is the ROC(ROC_trn2TST) of the model's prediction performance statistics to TST.
4.3. Test Results for Conditional Independence
The independence of 14 factors with AUCs>0.59 was analyzed (Figure 21). Figure 21 combines the statistical results of two correlation indexes, Pearson’s C and Cramer's V, which are located in the upper right half and the lower left half of the heat map, respectively. The results show that according to Pearson’s C index, Rou and TRI (0.81) and Rou and SL (0.71) are strongly correlated factor pairs. However, according to Cramer's V, the correlation among the factors involved in statistics is not strong (≤0.60). DF, HANDH and dCN have a low correlation with all other factors. Elevation and its derived TRI, Rou, RSP and SL are slightly related.
4.4. Step-by-step Modeling Results of Landslide Susceptibility
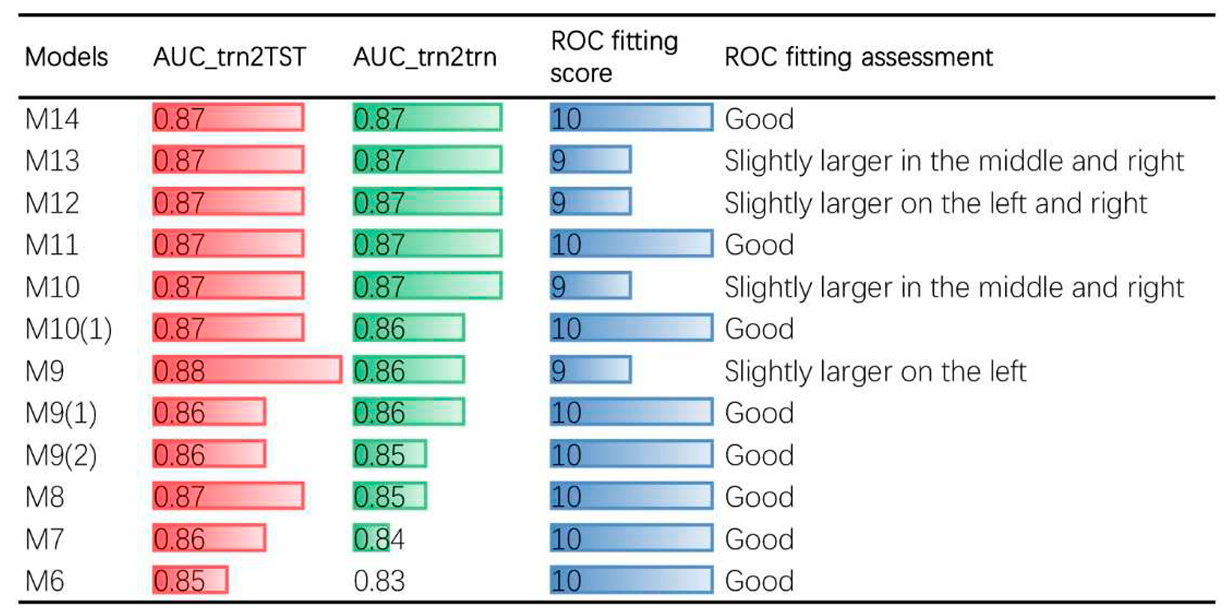
(1) Comprehensively considering the independence indexes of the factors, such as Pearson’s C and Cramer's V, and AUCs (AUC_trn, AUC_trn2trn and AUC_trn2TST), six factors with AUC_trn ≥0.63, AUC_trn2trn ≥0.63 and AUC_trn2tst ≥0.64 were selected for modeling, including dRD, HANDV, NDVIlog, SL, RSP and TRI.
(2) On the basis of M6, Rou and HANDH with AUC_trn≥ 0.64, AUC_trn2trn≥ 0.62 and AUC_trn2TST≥ 0.61 were added in turn. A seven-factor model (M7) and an eight-factor model (M8) was constructed, respectively, which improved AUC_M and were selected as the basic models for the next modeling step.
(3) On the basis of M8, we tried to increase dF, Lth and dCN with indexes ≥ 0.63, ≥ 0.62 and ≥ 0.60 and construct M9, M9 (1) and M9 (2). M9, M9 (1) and M9 (2) have different degrees of improvement compared with M8, especially M9. We took M9 as the basis of the next modeling step.
(4) On the basis of M9, M10 (M9+Lth) and M10(1) (M9+dCN) were compared, and the AUC of M10 model was higher than that of M9, so it was selected as the basis for the next modeling step.
(5) On the basis of M10, M11 (M10+dCN) was tested. Although the AUC of the model did not increase, the coincidence between ROC_M_trn2trn and ROC_M_trn2TST was significantly improved.
(6) On the basis of M11, M12 (M11 + CProf), M13 (M11 + CProf + CLCD) and M14 (M11 + CProf + CLCD + DEM) were tested. Compared with M11, M12 not only did not improve AUC_M, but also the coincidence between ROC_M_trn2trn and ROC_M_trn2TST became worse. Compared with M11, although ROC_M_trn2trn and ROC_M_trn2TST were in good agreement, AUC_M was not improved. Therefore, the effect of adding CProf, CLCD and DEM to M11 was not obvious.
(7) To sum up, the model M11 is the best model.
As shown in Figure 22, the success rate of the model M11 is represented by the ROC calculated by using trn, and its AUC index is ~0.87. The AUC index of the prediction rate calculated using TST was ~0.87 too. Both of them are high, being within the range of excellent classification models. The results show that 11 factors are enough to create the most effective map of landslide susceptibility in the study area.
Table 2.
Comparison of validity and accuracy (AUCs) of models.
4.5. Landslide Susceptibility Mapping Results
Based on the ROC_M_trn2trn of model M11, we compiled the landslide susceptibility zoning map (Figure 23). Very-high-susceptibility areas (VHS), which comprise only 5.05% of the study area, contain 50% of landslides, and high-susceptibility areas (HS), which comprise 14.53% of the study area, contain 30% of landslides (Figure 23, Table 3). Therefore, the high-susceptibility (HS) and the very-high-susceptibility areas (VHS), with an area accounting for 19.58% of the study areas, containing 80% of the landslides. These characteristics of the landslide susceptibility zoning map represent the potential for the first-order prediction of landslides in this landscape.
5. Discussion
5.1. Landslide Susceptibility Zoning and Disaster Prevention Deployment Strategy
Based on the above work, we compiled the landslide susceptibility map of the Dianchi Lake watershed, which has great practical significance. The map provides basic information relating to landslide disasters for spatial planners. It can be used to determine the regional priority for further investigation, support the local planning activities of regional geological disaster prevention and ecological restoration, or create a regional landslide risk exposure assessment. The latter can evaluate the existing elements with landslide risk or those still under planning.
The landslide susceptibility map developed in this paper can effectively predict known and unknown landslides. The fitting accuracy and prediction accuracy of the best model M11 are both ~0.87, and the model coincidence is excellent (Figure 22, Table 2). Moreover, ROC_M_trn2TST is in good coincidence with the range of ROC_M_trn2trn (Figure 22, Table 2), indicating that there is no over-fitting or under-fitting. When 19.58% of the research area is defined as high susceptibility (VHS+HS), the model predicts 80% of the landslides (Figure 23, Table 3). The above results obtained from the analysis are satisfactory for the Dianchi Lake watershed.
The landslide susceptibility map developed in this paper reveals that the area with high susceptibility (VHS+HS) is large, accounting for ~20% of study area (excluding the area with flat and water surface), which shows that the natural landslide susceptibility intensity in the Dianchi Lake Watershed is large, which poses a great challenge for the comprehensive prevention and control of geological disasters, and this work has a long way to go. In particular, there are large areas of high susceptibility (VHS+HS) in the mountainous area of the northern basin edge of Kunming urban area, and it is almost contiguous. These areas are close to Kunming city and Dianchi Lake waters, which have great influence on urban safety and Dianchi Lake water protection, and should be taken as the key areas for landslide prevention and control. Another area with high susceptibility (VHS+HS) is the southeast of the study area, which should also be subjected to mitigation and preventative activities.
5.2. Important Factors of Landslide Susceptibility and High Sensitivity and Disaster Prevention Strategies
AUCs (AUC_ALL, AUC_trn, AUC_trn2trn, AUC_trn2TST) of single factors quantify the sensitivity (spatial correlation) of the landslide impact of each factor, and the weight of evidence of single factors (WoE_ALL, WoE_trn) reveals the impact of each classification on the spatial distribution of landslide,while sC defines the significance of the difference between classifications. AUCs, WoEs and sCs are meaningful indicators to quantify the sensitivity of landslide impact.
We have identified more reliable landslide control factors. The analysis results of this paper (Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19 and Figure 20) show 13 factors with AUC ≥ 0.6 from high to low AUC: dRD, HANDV, NDVIlog, SL, RSP, TRI, Rou, Lth, dF, HANDH, Cprof, dCN, and CLCD (Table 4). The optimal landslide susceptibility model represents a combination of 11 factors: dRD, HANDV, NDVIlog, SL, RSP, TRI, Rou, Lth, dF, HANDH, and dCN. In the process of step-by-step modeling, Cprof, dCN and CLCD were all rejected because they did not contribute to the explanatory power of the model, as evaluated using ROC_M.
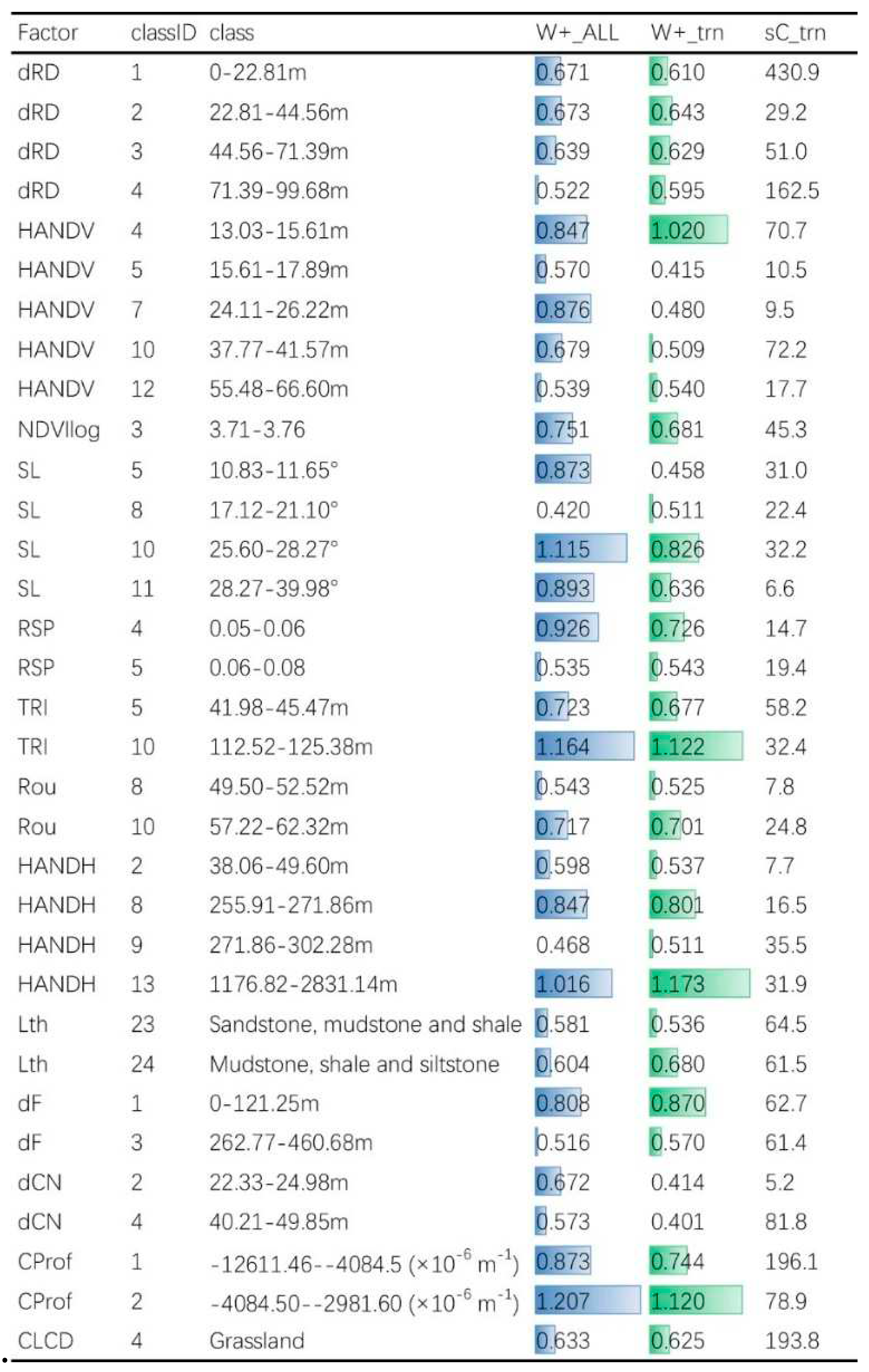
We pay attention to which classification of the above important factors is more conducive to the occurrence of landslides. We analyzed the factor classification of (Table 5).
The above results suggest that we should pay attention to the natural conditions and human factors represented by dRD, HANDV, NDVIlog, SL, RSP, TRI, Rou, Lth, dF, HANDH, dCN, CProf and CLCD, coordinate prevention with planning, construction and protection, and reduce the induction of landslides. Attention should be paid to the slope stability support within 100m on both sides of the road, and development should be reduced in steep slope areas (25-40°), in areas where the height difference between the two sides of the stream is 13-67m and in low vegetation coverage areas. Attention should be paid to the conservation and protection of forest vegetation, and the distribution map should be used to avoid weak rocks such as the affected areas of fault zones and shale siltstone.
5.3. The Landslide Susceptibility Evaluation Based on the WoE Method May be Improved
The optimized classification process sets the classification value based on the nearly continuous cumulative sC curve of evidence weight distribution and then carries out WoE statistics, which captures the trend of evidence weight distribution, overcomes the discontinuity of evidence weight distribution in traditional methods, improves the discrimination of landslide sensitivity of each influencing factor and reduces the subjectivity of factor classification.
The uncertainty analysis obtained by using sub-sampling cross-validation technology allows us to verify the weighted uncertainty sampling process related to the introduced error [6]. The trn and TST are spatial random sub-samples of the same size from the same dataset, ALL, which represent the same spatial distribution but have different mean sampling error (MSE) related to sample size [4]. The model performance evaluation based on TST, which is smaller than TRN, must take this into account in order to correctly interpret the model analysis results [16]. MSE based on trn defines the uncertainty of model performance. If the model is well summarized and there is no obvious over-fitting, the ROC curve and AUC value should fall within the MSE range when evaluating the model with corresponding TST [4]. Therefore, compared with no sampling (analysis with all landslide data), this analysis is advantageous because the potential impact of random sub-sampling is considered.
We compared the accuracy and predictive performance of 14 models with different factor combinations. The optimal model M11 determined in this paper contains Rou, TRI and SL with Pearson’s C index > 0.7, but the ROC_M_trn2TST of the model not only does not show over-fitting, but also shows excellent coincidence. We think that it is not appropriate to exclude the modeling factors only according to Pearson’s C index, and it may be more feasible to comprehensively determine the Cramer's V index and ROC_M.
The improved comprehensive process proposed in this paper combines many techniques, such as optimized classification, cross-validation and step-by-step modeling, and obtains the model with high accuracy and predictive performance, which shows that this process has good practical value and may improve the landslide susceptibility evaluation based on the WoE method, which is worthy of further promotion and application in similar areas.
5.4. Restrictions
According to the research of [46], the abundance of landslide list is a critical resource that affects susceptibility modeling, and is more important than the detailed data of influencing factors. The landslide data used in this paper may be incomplete, which may have some influence on the analysis results of this paper. In the future, it is necessary to strengthen the compilation of a more complete landslide inventory based on remote sensing.
Regarding the improved technical process and factor classification optimization process of the landslide susceptibility evaluation model based on WoE method put forward in this paper, although more effective modeling results have been obtained in the research area, it still requires more demonstration areas for testing. Furthermore, the process proposed in this paper is not highly automated and needs more manual intervention. In the future, research should be deepened to form a more convenient data-driven process.
6. Conclusion
Dianchi Lake is the largest of the nine plateau lakes in Yunnan Plateau. These nine plateau lake watersheds are important ecological protection areas in southwest China. It is of great practical significance to evaluate and analyze the landslide susceptibility in the Dianchi Lake watershed for disaster prevention and mitigation, ecological protection and restoration planning. In this paper, firstly, a factor optimization classification process was developed on the basis of the traditional WoE method, and the landslide susceptibility evaluation process based on the WoE method was perfected. Based on the spatial distribution data of historical landslides, a factor classification scheme was put forward, the landslide susceptibility sensitivity of each factor was evaluated, the important landslide susceptibility control factors were screened out, the landslide susceptibility evaluation model was established, and the landslide susceptibility distribution in the study area was evaluated and analyzed. The main conclusions are as follows:
(1) An improved technical process of landslide susceptibility assessment model based on the WoE method was put forward and successfully applied, a factor classification optimization process was developed, and a highly effective model (AUC=0.87) was established, which made a new contribution to the improvement of landslide susceptibility assessment technology based on the WoE method.
(2) According to the results, eleven factors, such as dRD, HANDV, NDVIlog, SL, RSP, TRI, Rou, Lth, dF, HANDH, and dCN, were identified as the key sensitive factors of landslide in the study area, which should be considered in landslide prevention, monitoring and early warning facility layout and ecological restoration planning.
(3) The landslide susceptibility map developed in this paper reveals that the area of high susceptibility (VHS+HS) in the Dianchi Lake watershed is large, and the comprehensive prevention and control of landslides have a long way to go. The large-scale and contiguous high-susceptibility areas in the mountainous areas on the edge of the basin present the urban safety of Kunming and the water protection of Dianchi Lake with serious landslide hazards, and so the investigation, monitoring and risk assessment of landslide hazards should be strengthened.
Author Contributions
Conceptualization, G.B., X.Y. and Z.K.; methodology, G.B. and X.Y.; software, G.B. and X.Y.; validation, G.B., X.Y. and Z.K.; formal analysis, G.B. and X.Y.; investigation, G.B., X.Y., Z.K., J. Z., S. Z., and B.S.; resources, G.B. X.Y. and Z.K.; data curation, Z.K. and S.Z.; writing—original draft preparation, G.B., X.Y. and Z.K.; writing—review and editing, G.B., X.Y., Z.K., J.Z., B.S. and S.Z.; visualization, G.B. and X.Y.; supervision, Z.K. and S.Z.; project administration, S.Z. and J.Z.; funding acquisition, S.Z. and J.Z.. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the science and technology development project of Power China, Sinohydro Foundation Engineering Co., Ltd. (Tianjin, China), the evaluation of rapid excavation of slope cut-off wall in complex geological background area and treatment technology of mud and water inrush in tunnel engineering (Grant No. 2022530103001936), and the scientific and technological development project of Southwest Pipeline Co., Ltd. (Chengdu, China), National Pipe Network Group Research on Hydraulic Protection and Soil and Water Conservation of Oil and Gas Pipelines through Fully Weathered Granite Area (Grant No. 2018016).
Data Availability Statement
The datasets for this study can be obtained by contacting the first author or corresponding author.
Acknowledgments
We are very grateful to the colleagues in the team who supported the implementation of this project. We are sincerely thankful to Torizin J. for providing data processing software LSAT PM. We are also sincerely thankful to the editors and reviewers.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Regmi, N.R.; Giardino, J.R.; Vitek, J.D. Modeling susceptibility to landslides using the weight of evidence approach: Western Colorado, USA. Geomorphology 2010, 115, 172–187. [Google Scholar] [CrossRef]
- Bai, G.; Yang, X.; Zhu, J.; Zhang, S.; Zhu, C.; Kang, X.; Sun, B.; Zhou, Y. Susceptibility assessment of geological hazards in Wuhua District of Kuming, China using the weight evidence method. The Chinese Journal of Geological Hazard and Control 2022, 33, 128–138. [Google Scholar]
- Guzzetti, F.; Reichenbach, P.; Cardinali, M.; Galli, M.; Ardizzone, F. Probabilistic landslide hazard assessment at the basin scale. Geomorphology 2005, 72, 272–299. [Google Scholar] [CrossRef]
- Torizin, J.; Schüßler, N.; Fuchs, M. Landslide Susceptibility Assessment Tools v1.0.0b – Project Manager Suite: a new modular toolkit for landslide susceptibility assessment. Geosci Model Dev 2022, 15, 2791–2812. [Google Scholar] [CrossRef]
- Guzzetti, F.; Cardinali, M.; Reichenbach, P.; Carrara, A. Comparing Landslide Maps: A Case Study in the Upper Tiber River Basin, Central Italy. Environ Manage 2000, 25, 247–263. [Google Scholar] [CrossRef]
- Torizin, J.; Fuchs, M.; Awan, A.A.; Ahmad, I.; Akhtar, S.S.; Sadiq, S.; Razzak, A.; Weggenmann, D.; Fawad, F.; Khalid, N.; et al. Statistical landslide susceptibility assessment of the Mansehra and Torghar districts, Khyber Pakhtunkhwa Province, Pakistan. Nat Hazards 2017, 89, 757–784. [Google Scholar] [CrossRef]
- Torizin, J.; Wang, L.; Fuchs, M.; Tong, B.; Balzer, D.; Wan, L.; Kuhn, D.; Li, A.; Chen, L. Statistical landslide susceptibility assessment in a dynamic environment: A case study for Lanzhou City, Gansu Province, NW China. J Mt Sci-Engl 2018, 15, 1299–1318. [Google Scholar] [CrossRef]
- Bonham-Carter, G.; Agterberg, F.P.; Wright, D.F. Weight of evidence modeling: A new approach to mapping mineral potential. Geology Survey of Canada 1989, 89, 171–183. [Google Scholar]
- Torizin, J. Elimination of informational redundancy in the weight of evidence method: an application to landslide susceptibility assessment. Stoch Env Res Risk A 2016, 30, 635–651. [Google Scholar] [CrossRef]
- Alsabhan, A.H.; Singh, K.; Sharma, A.; Alam, S.; Pandey, D.D.; Rahman, S.A.S.; Khursheed, A.; Munshi, F.M. Landslide susceptibility assessment in the Himalayan range based along Kasauli – Parwanoo road corridor using weight of evidence, information value, and frequency ratio. Journal of King Saud University - Science 2022, 34, 101759. [Google Scholar] [CrossRef]
- Chen, L.; Guo, H.; Gong, P.; Yang, Y.; Zuo, Z.; Gu, M. Landslide susceptibility assessment using weights-of-evidence model and cluster analysis along the highways in the Hubei section of the Three Gorges Reservoir Area. Comput Geosci-Uk 2021, 156, 104899. [Google Scholar] [CrossRef]
- Mathew, J.; Jha, V.K.; Rawat, G.S. Weights of evidence modelling for landslide hazard zonation mapping in part of Bhagirathi valley, Uttarakhand. Current Science (Bangalore) 2007, 92, 628–638. [Google Scholar]
- Neuhäuser, B.; Terhorst, B. Landslide susceptibility assessment using “weights-of-evidence” applied to a study area at the Jurassic escarpment (SW-Germany). Geomorphology 2007, 86, 12–24. [Google Scholar] [CrossRef]
- Saha, A.; Saha, S. Comparing the efficiency of weight of evidence, support vector machine and their ensemble approaches in landslide susceptibility modelling: A study on Kurseong region of Darjeeling Himalaya, India. Remote Sensing Applications: Society and Environment 2020, 19, 100323. [Google Scholar] [CrossRef]
- Teerarungsigul, S.; Torizin, J.; Fuchs, M.; Kühn, F.; Chonglakmani, C. An integrative approach for regional landslide susceptibility assessment using weight of evidence method: a case study of Yom River Basin, Phrae Province, Northern Thailand. Landslides 2016, 13, 1151–1165. [Google Scholar] [CrossRef]
- Torizin, J.; Fuchs, M.; Kuhn, D.; Balzer, D.; Wang, L. Practical Accounting for Uncertainties in Data-Driven Landslide Susceptibility Models. Examples from the Lanzhou Case Study. In Understanding and Reducing Landslide Disaster Risk: Volume 2 From Mapping to Hazard and Risk Zonation, Guzzetti, F., Mihalić Arbanas, S., Reichenbach, P., Sassa, K., Bobrowsky, P.T., Takara, K., Eds.; Springer International Publishing: Cham, 2021; pp. 249–255. [Google Scholar]
- Jasiewicz, J.; Stepinski, T.F. Geomorphons — a pattern recognition approach to classification and mapping of landforms. Geomorphology 2013, 182, 147–156. [Google Scholar] [CrossRef]
- Stepinski, T.F.; Jasiewicz, J. Geomorphons - a new approach to classification of landforms. Proceedings of Geomorphometry 2011, Hengl, T.; Evans, I.S.; Wilson, J.P.; Gould, M.,Eds. Redlands; 2011; pp. 109–112. [Google Scholar]
- Yang, J.; Huang, X. The 30m annual land cover dataset and its dynamics in China from 1990 to 2019. Earth Syst Sci Data 2021, 13, 3907–3925. [Google Scholar] [CrossRef]
- Chung, C.; Fabbri, A.G. Predicting landslides for risk analysis — Spatial models tested by a cross-validation technique. Geomorphology 2008, 94, 438–452. [Google Scholar] [CrossRef]
- Xu, Y.; Goodacre, R. On Splitting Training and Validation Set: A Comparative Study of Cross-Validation, Bootstrap and Systematic Sampling for Estimating the Generalization Performance of Supervised Learning. J Anal Test 2018, 2, 249–262. [Google Scholar] [CrossRef]
- He, Q.; Wang, M.; Liu, K. Rapidly assessing earthquake-induced landslide susceptibility on a global scale using random forest. Geomorphology 2021, 391, 107889. [Google Scholar] [CrossRef]
- Lan, H.; Tian, N.; Li, L.; Wu, Y.; Macciotta, R.; Clague, J.J. Kinematic-based landslide risk management for the Sichuan-Tibet Grid Interconnection Project (STGIP) in China. Eng Geol 2022, 308, 106823. [Google Scholar] [CrossRef]
- Tanyaş, H.; Görüm, T.; Fadel, I.; Yıldırım, C.; Lombardo, L. An open dataset for landslides triggered by the 2016 Mw 7.8 Kaikōura earthquake, New Zealand. Landslides 2022, 19, 1405–1420. [Google Scholar] [CrossRef]
- Xiong, H.; Ma, C.; Li, M.; Tan, J.; Wang, Y. Landslide susceptibility prediction considering land use change and human activity: A case study under rapid urban expansion and afforestation in China. Sci Total Environ 2023, 866, 161430. [Google Scholar] [CrossRef]
- Zhang, Y.; Ayyub, B.M.; Gong, W.; Tang, H. Risk assessment of roadway networks exposed to landslides in mountainous regions—a case study in Fengjie County, China. Landslides 2023. [Google Scholar] [CrossRef]
- Guzzetti, F.; Mondini, A.C.; Cardinali, M.; Fiorucci, F.; Santangelo, M.; Chang, K. Landslide inventory maps: New tools for an old problem. Earth-Sci Rev 2012, 112, 42–66. [Google Scholar] [CrossRef]
- Zanaga, D.; Van De Kerchove, R.; De Keersmaecker, W.; Souverijns, N.; Brockmann, C.; Quast, R.; Wevers, J.; Grosu, A.; Paccini, A.; Vergnaud, S.; et al. ESA WorldCover 10 m 2020 v100 [Data set]. In 2021.
- Xu, X. China 30m Annual NDVI Maximum Dataset [Data set]. Resource and Environmental Science Data Registration and Publishing System 2022. [Google Scholar]
- JPL, N. NASADEM Merged DEM Global 1 arc second V001. Accessed 2020-12-30 from doi:10.5067/MEaSUREs/NASADEM/NASADEM_HGT.001 [Data set]. Nasa Eosdis Land Processes Daac. 2020. [CrossRef]
- Guisan, A.; Weiss, S.B.; Weiss, A.D. GLM versus CCA spatial modeling of plant species distribution. Plant Ecol 1999, 143, 107–122. [Google Scholar] [CrossRef]
- Riley, S.; Degloria, S.; Elliot, S.D. A Terrain Ruggedness Index that Quantifies Topographic Heterogeneity. Internation Journal of Science 1999, 5, 23–27. [Google Scholar]
- Nobre, A.D.; Cuartas, L.A.; Hodnett, M.; Rennó, C.D.; Rodrigues, G.; Silveira, A.; Waterloo, M.; Saleska, S. Height Above the Nearest Drainage – a hydrologically relevant new terrain model. J Hydrol 2011, 404, 13–29. [Google Scholar] [CrossRef]
- Rennó, C.D.; Nobre, A.D.; Cuartas, L.A.; Soares, J.V.; Hodnett, M.G.; Tomasella, J.; Waterloo, M.J. HAND, a new terrain descriptor using SRTM-DEM: Mapping terra-firme rainforest environments in Amazonia. Remote Sens Environ 2008, 112, 3469–3481. [Google Scholar] [CrossRef]
- Moore, I.D.; Grayson, R.B.; Ladson, A.R. Digital terrain modelling: A review of hydrological, geomorphological, and biological applications. Hydrol Process 1991, 5, 3–30. [Google Scholar] [CrossRef]
- Beven, K.; Kirkby, M. A Physically Based, Variable Contributing Area Model of Basin Hydrology. Hydrol. Sci. Bull. 1979, 24, 43–69. [Google Scholar] [CrossRef]
- Böhner, J.; Selige, T. Spatial prediction of soil attributes using terrain analysis and climate regionalisation. Saga - Analysis and Modelling Applications 2006, 115, 13–27. [Google Scholar]
- Böhner, J.; Koethe, R.; Conrad, O.; Gross, J.; Ringeler, A.; Selige, T. Soil regionalisation by means of terrain analysis and process parameterisation. Soil Classification 2001 2002, 213–222. [Google Scholar]
- Agterberg, F.P.; Bonham-Carter, G.F.; Cheng, Q.; Wright, D.F.; Davis, J.C.; Herzfeld, U.C. Weights of evidence modeling and weighted logistic regression for mineral potential mapping. Computers in Geology--25 Years of Progress 1993, 5, 13–32. [Google Scholar]
- Agterberg, F.P. Combining indicator patterns in weights of evidence modeling for resource evaluation. Nonrenewable Resources 1992, 1, 39–50. [Google Scholar] [CrossRef]
- Agterberg, F.P.; Bonham-Carter, G.F.; Wright, D.F. Statistical Pattern Integration for Mineral Exploration**Geological Survey of Canada Contribution No. 24088. In Computer Applications in Resource Estimation, GAÁL, G.; MERRIAM, D.F., Ed.; Pergamon: Amsterdam, 1990; pp. 1–21. [Google Scholar]
- Bonham-Carter, G.F. Geographic Information Systems for Geoscientists: Modelling with GIS. Pergamon: Canada, 1994; p 1-398.
- Fawcett, T. An introduction to ROC analysis. Pattern Recogn Lett 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Agterberg, F.P.; Cheng, Q. Conditional Independence Test for Weights-of-Evidence Modeling. Nat Resour Res 2002, 11, 249–255. [Google Scholar] [CrossRef]
- Chung, C.F.; Fabbri, A.G. Validation of Spatial Prediction Models for Landslide Hazard Mapping. Nat Hazards 2003, 30, 451–472. [Google Scholar] [CrossRef]
- Depicker, A.; Jacobs, L.; Delvaux, D.; Havenith, H.; Maki Mateso, J.; Govers, G.; Dewitte, O. The added value of a regional landslide susceptibility assessment: The western branch of the East African Rift. Geomorphology 2020, 353, 106886. [Google Scholar] [CrossRef]
Figure 1.
Study area. (a) The location of Yunnan province in China. (b) The distribution of nine plateau lake watersheds in Yunnan, and the location of the Dianchi Lake watershed. The base map is the distribution map of land coverage types in Yunnan Province in 2020 [19]; (c) The distribution map of landslide points in Dianchi Lake watershed, the black points are landslides under investigation, the blue blocks are the water surface, and the gray diagonal lines are the areas with the attribute of "flat" [17,18], and the bottom picture is rendered by elevation and hill shade.
Figure 1.
Study area. (a) The location of Yunnan province in China. (b) The distribution of nine plateau lake watersheds in Yunnan, and the location of the Dianchi Lake watershed. The base map is the distribution map of land coverage types in Yunnan Province in 2020 [19]; (c) The distribution map of landslide points in Dianchi Lake watershed, the black points are landslides under investigation, the blue blocks are the water surface, and the gray diagonal lines are the areas with the attribute of "flat" [17,18], and the bottom picture is rendered by elevation and hill shade.
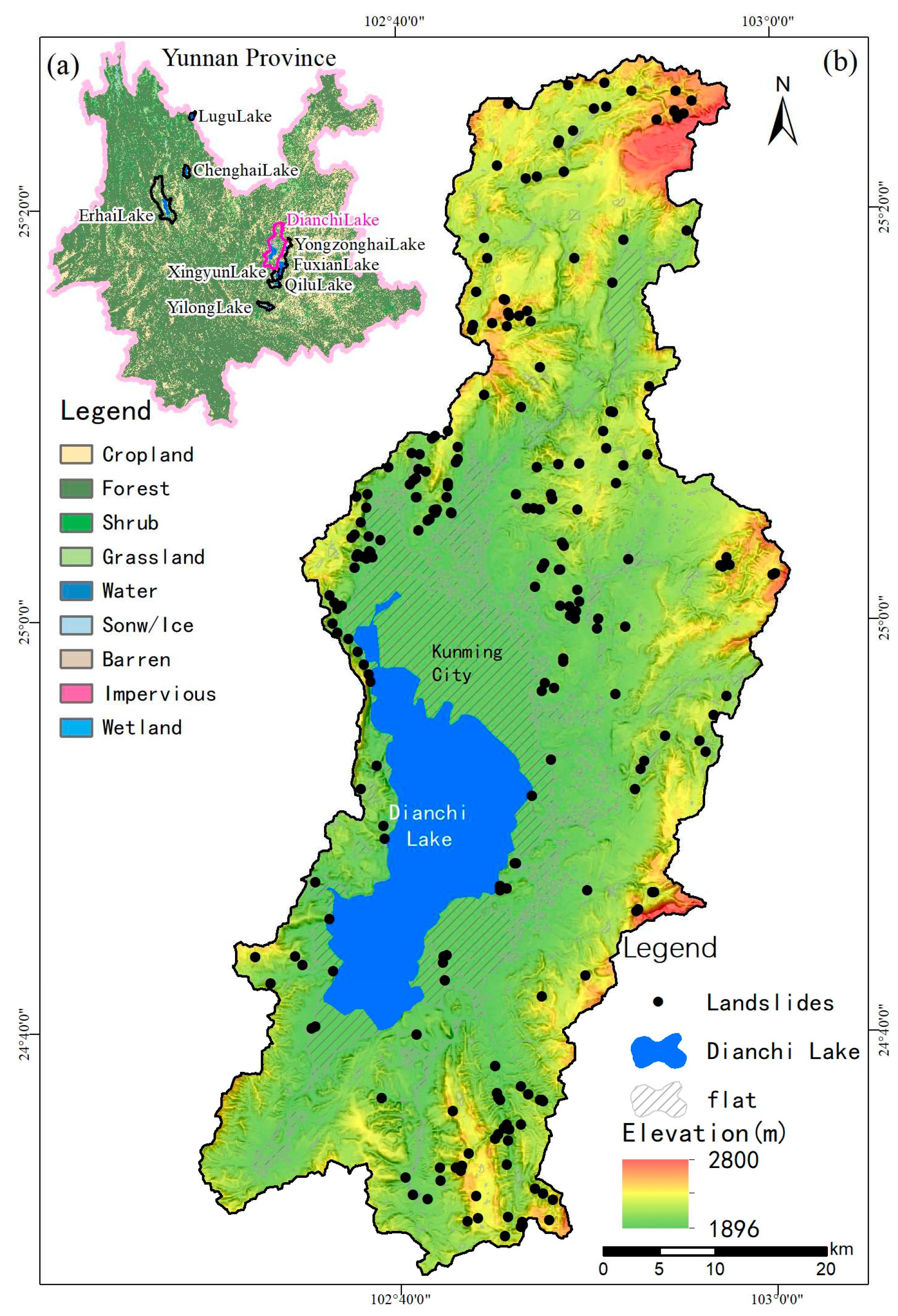
Figure 2.
Process flow chart of cross-validation landslide dataset compilation based on random sampling.
Figure 2.
Process flow chart of cross-validation landslide dataset compilation based on random sampling.
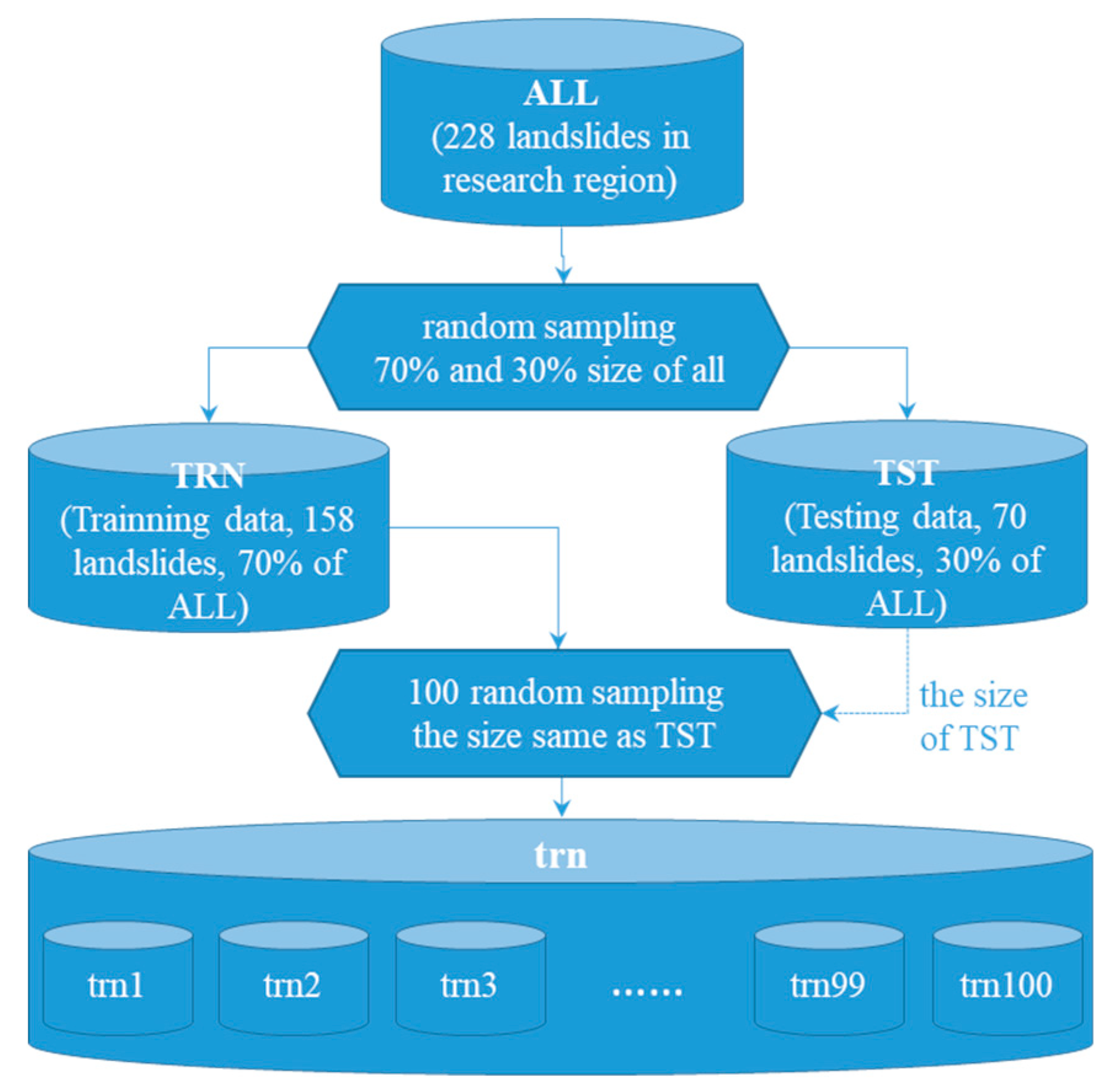
Figure 6.
Process flow chart of factor classification optimization strategy based on the cumulative sC curve and WoE statistics.
Figure 6.
Process flow chart of factor classification optimization strategy based on the cumulative sC curve and WoE statistics.
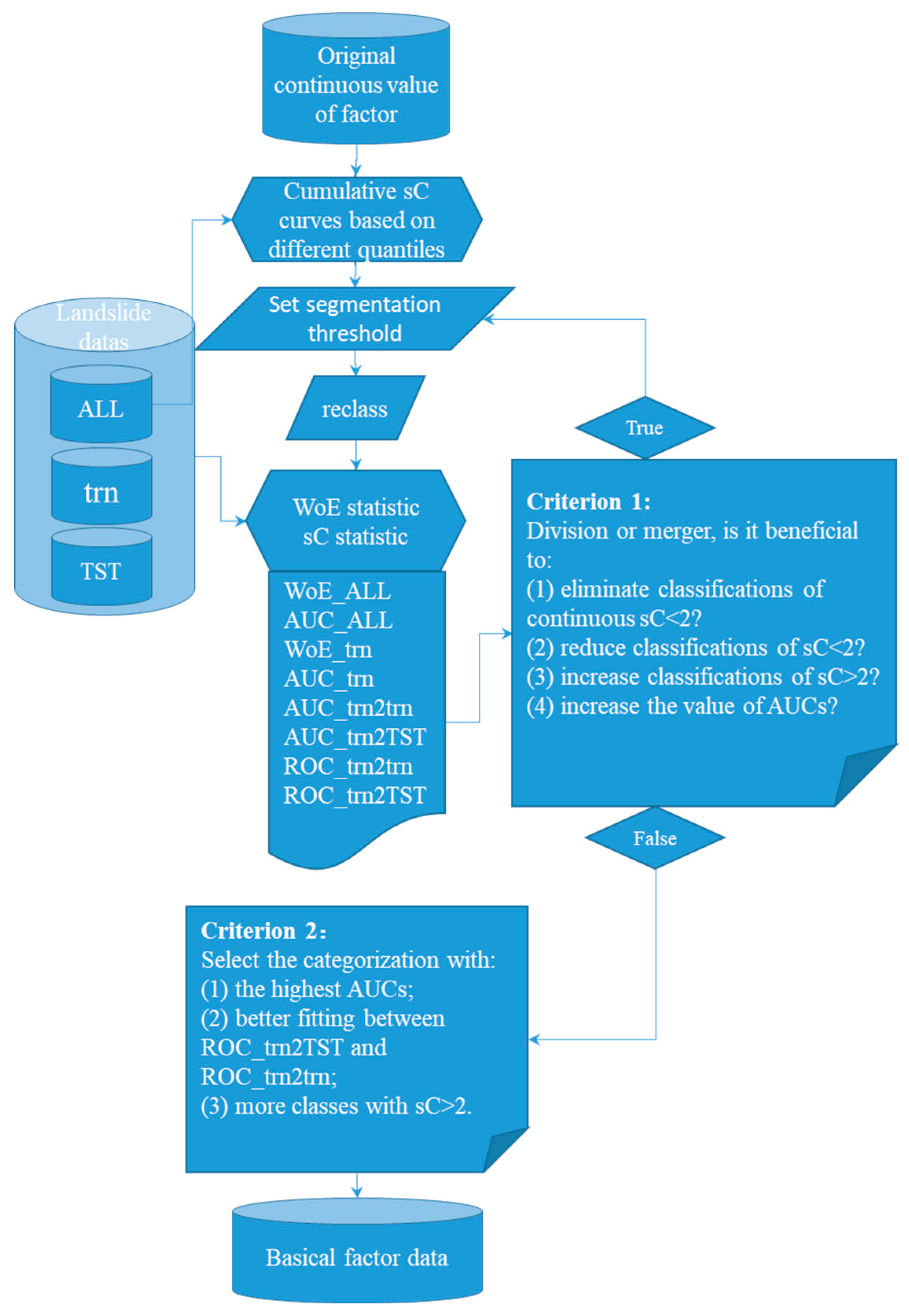
Figure 7.
The frequency distribution of some factors' original data and the cumulative sC statistical curve of multiple quantiles. There are two statistical result graphs for each factor—the upper graph is the frequency distribution graph of the original factor data, and the lower graph is the cumulative sC curve of statistics after the original factor data are dispersed according to six quantiles of 100, 80, 60, 40, 20 and 10.
Figure 7.
The frequency distribution of some factors' original data and the cumulative sC statistical curve of multiple quantiles. There are two statistical result graphs for each factor—the upper graph is the frequency distribution graph of the original factor data, and the lower graph is the cumulative sC curve of statistics after the original factor data are dispersed according to six quantiles of 100, 80, 60, 40, 20 and 10.
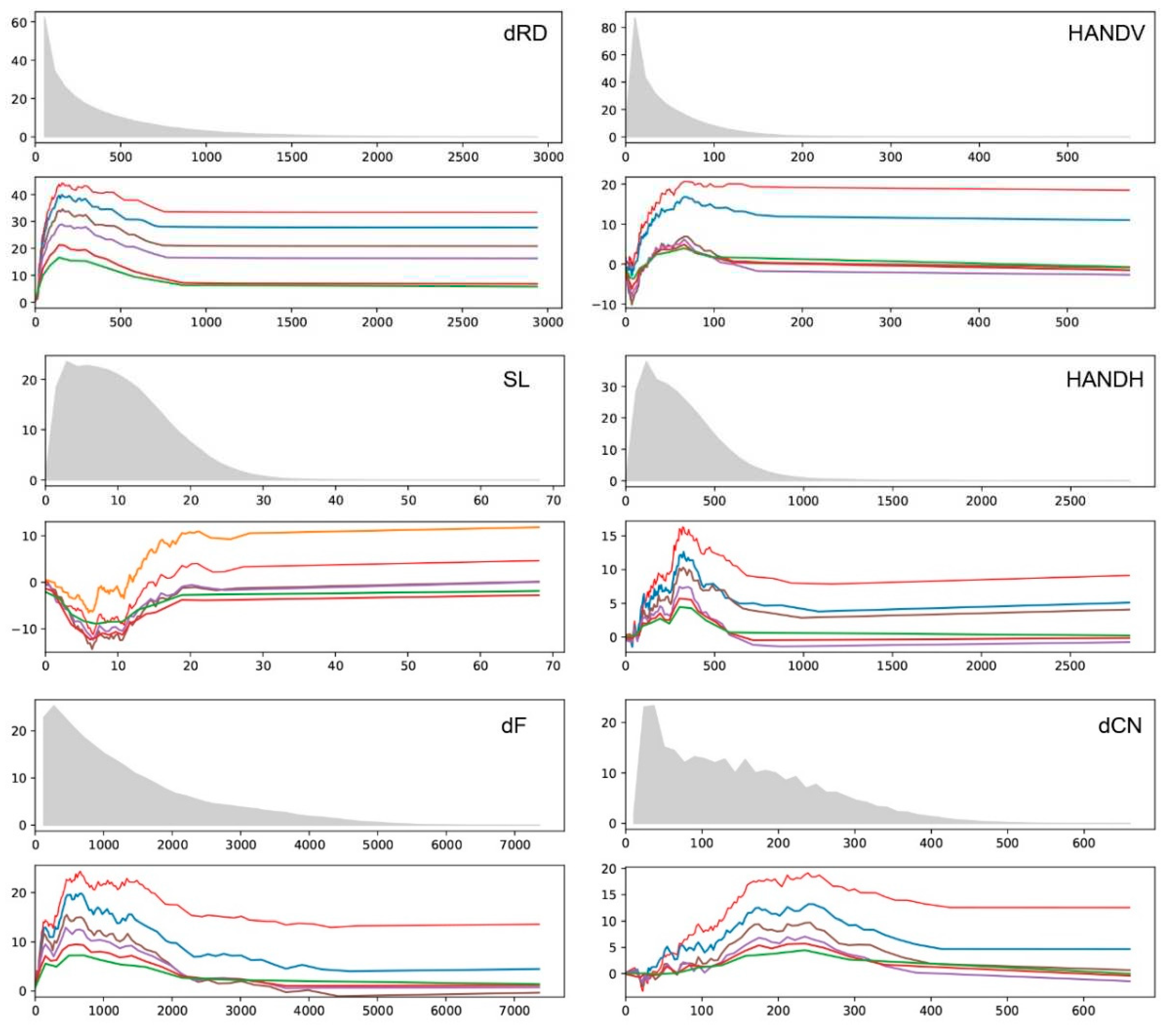
Figure 8.
Graphical result output of WoE analysis for the factor dF. Class 1 is 0-121m; class 3 is 262-460m; class 5 is 657-864m; class 7 is 1355-2317m; and class 99 is other ranges.
Figure 8.
Graphical result output of WoE analysis for the factor dF. Class 1 is 0-121m; class 3 is 262-460m; class 5 is 657-864m; class 7 is 1355-2317m; and class 99 is other ranges.
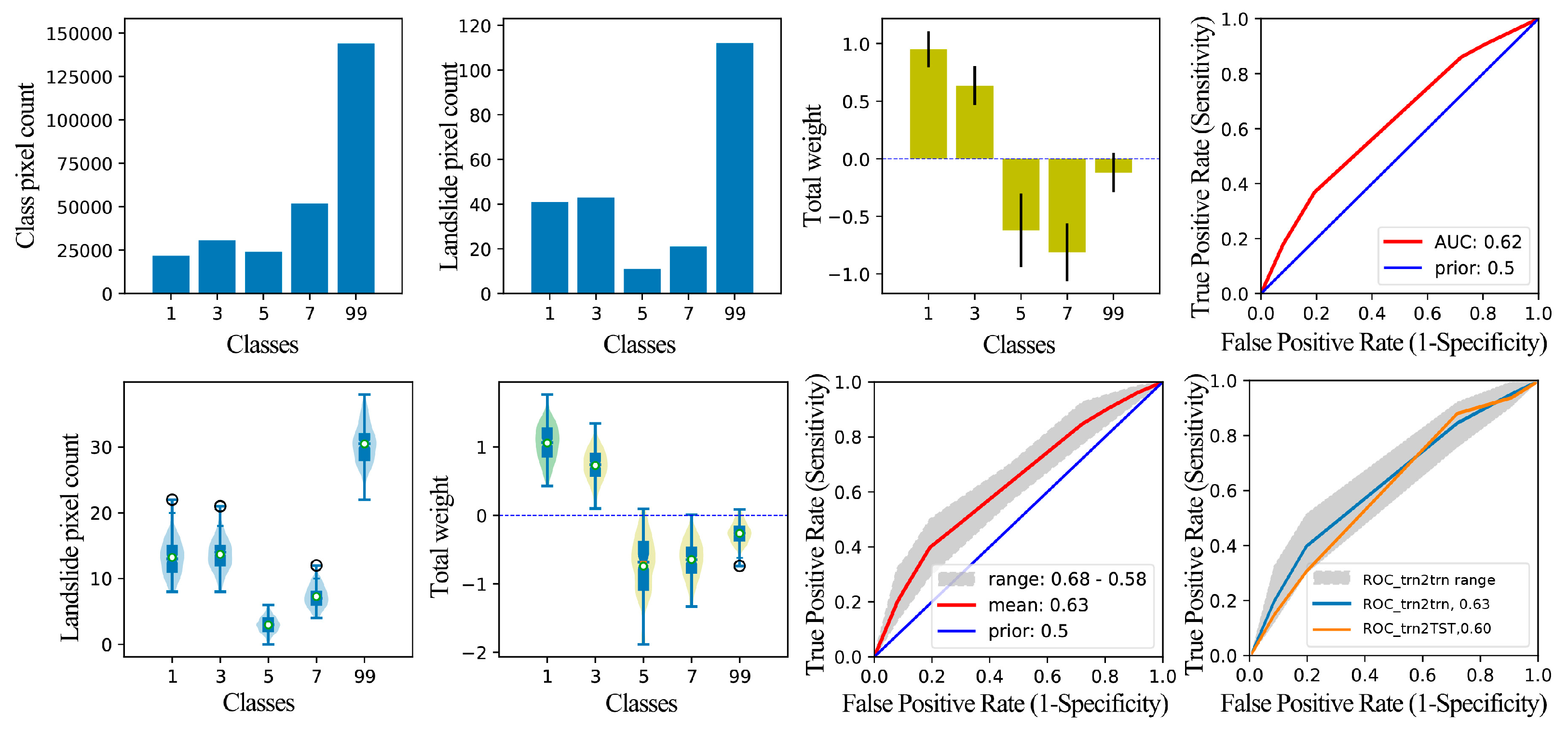
Figure 9.
Graphical result output of WoE analysis for the factor Lth. Class 10 is loose gravel soil, class 23 is sandstone, mudstone and shale, class 24 is mudstone, shale and siltstone, class 51 is basalt and class 199 is other lithologic strata, including limestone and metamorphic rocks.
Figure 9.
Graphical result output of WoE analysis for the factor Lth. Class 10 is loose gravel soil, class 23 is sandstone, mudstone and shale, class 24 is mudstone, shale and siltstone, class 51 is basalt and class 199 is other lithologic strata, including limestone and metamorphic rocks.
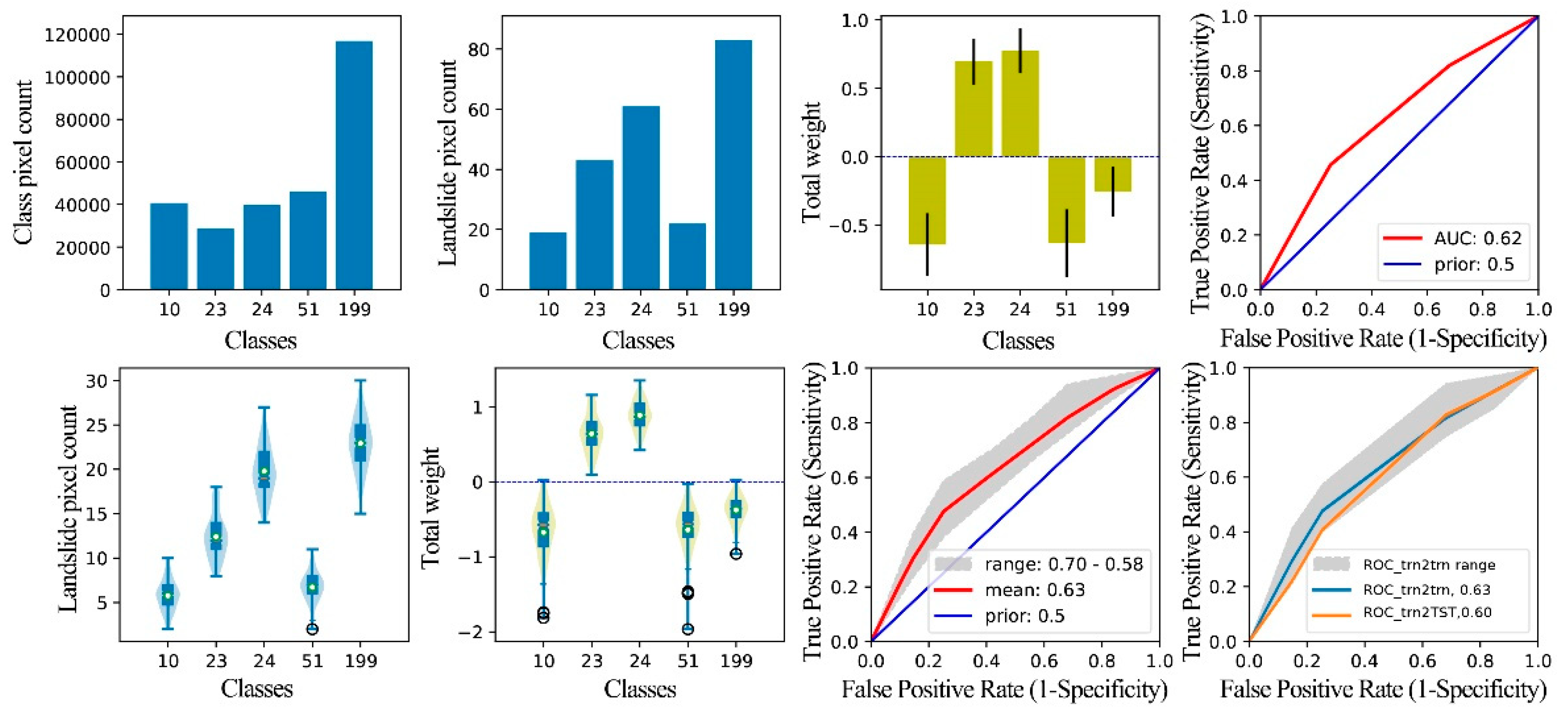
Figure 10.
Graphical result output of WoE analysis for the factor NDVIlog. Class 1 is 2.79-3.64, class 2 is 3.64-3.71, class 3 is 3.71-3.76, class 4 is 3.76-3.81, class 5 is 3.81-3.84, class 6 is 3.84-3.85, class 7 is 3.85-3.88, and class 8 is 3.88-3.99.
Figure 10.
Graphical result output of WoE analysis for the factor NDVIlog. Class 1 is 2.79-3.64, class 2 is 3.64-3.71, class 3 is 3.71-3.76, class 4 is 3.76-3.81, class 5 is 3.81-3.84, class 6 is 3.84-3.85, class 7 is 3.85-3.88, and class 8 is 3.88-3.99.
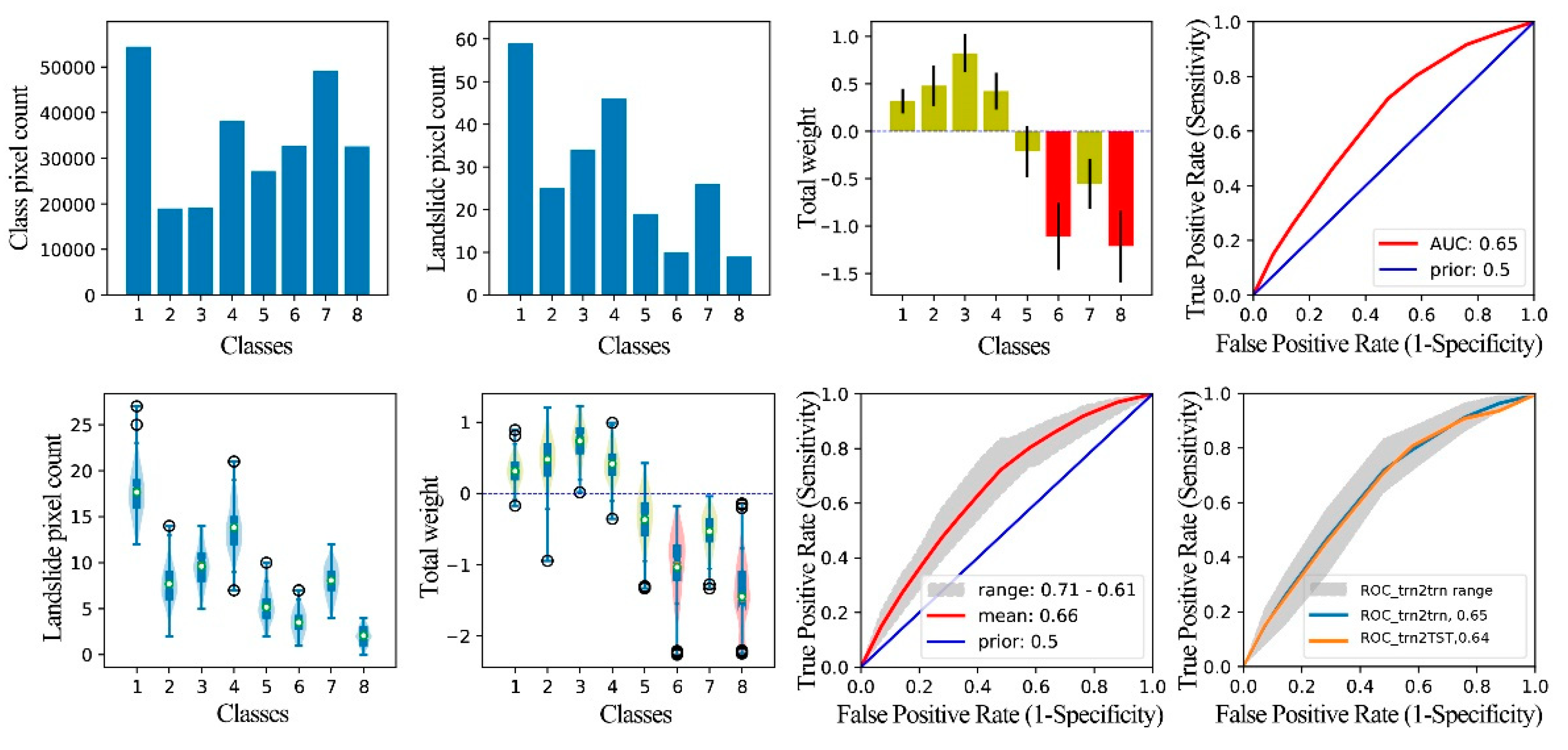
Figure 11.
Graphical result output of WoE analysis for the factor dRD. Class 1 is 0-22.81m, class 2 is 22.81-44.56m, class 3 is 44.56-71.39m, class 4 is 71.39-99.68m, class 5 is 99.68-157.42m, class 6 is 157.42-306.85m, class 7 is 306.85-458.95m, class 8 is 458.95-602.39m, and class 9 is 602.39-2936.07m.
Figure 11.
Graphical result output of WoE analysis for the factor dRD. Class 1 is 0-22.81m, class 2 is 22.81-44.56m, class 3 is 44.56-71.39m, class 4 is 71.39-99.68m, class 5 is 99.68-157.42m, class 6 is 157.42-306.85m, class 7 is 306.85-458.95m, class 8 is 458.95-602.39m, and class 9 is 602.39-2936.07m.
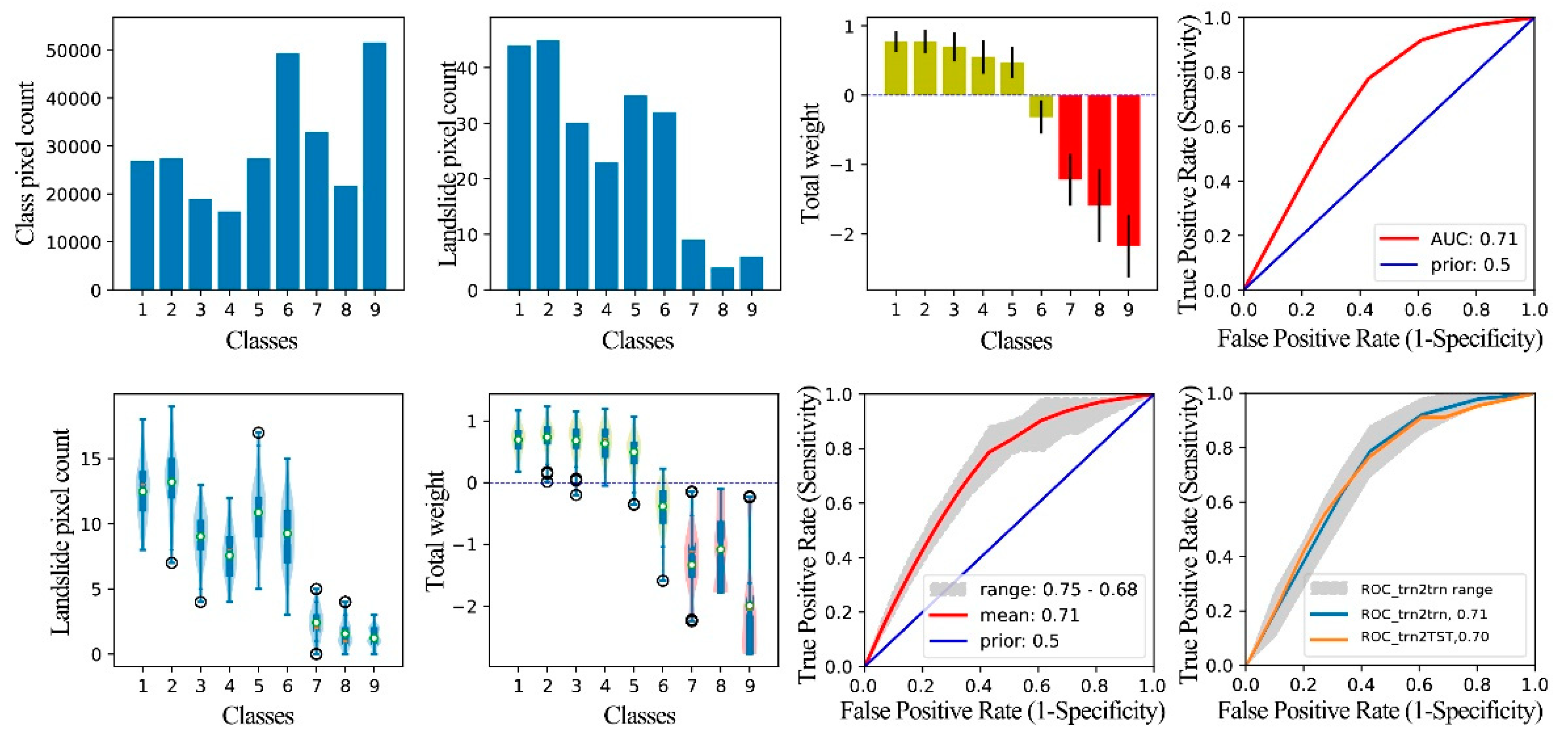
Figure 12.
Graphical result output of WoE analysis for the factor TRI. Class 1 is 0.00-11.58m, class 2 is 11.58-20.62m, class 3 is 20.62-22.98m, class 5 is 41.98-45.47m, class 7 is 48.89-52.50m, class 8 is 52.50-58.39m, class 10 is 112.52-125.38m, and class 99 is others in the range of 0-447.60m.
Figure 12.
Graphical result output of WoE analysis for the factor TRI. Class 1 is 0.00-11.58m, class 2 is 11.58-20.62m, class 3 is 20.62-22.98m, class 5 is 41.98-45.47m, class 7 is 48.89-52.50m, class 8 is 52.50-58.39m, class 10 is 112.52-125.38m, and class 99 is others in the range of 0-447.60m.
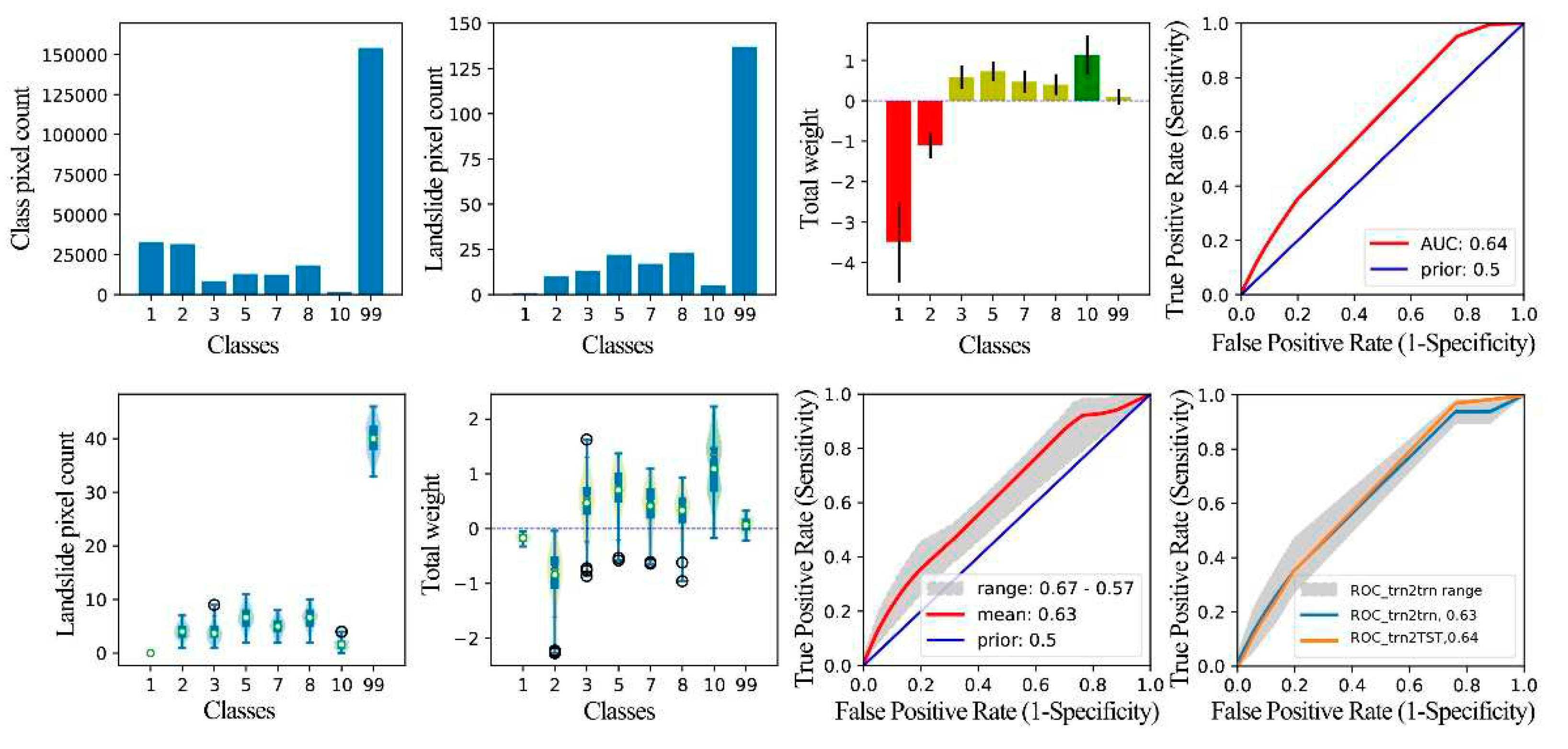
Figure 13.
Graphical result output of WoE analysis for the factor Rou. Class 1 is 0.00-8.93, class 2 is 8.93-16.53, class 3 is 16.53-24.95, class 4 is 24.95-28.88, class 5 is 28.88-40.73, class 6 is 40.73-44.33, class 7 is 44.33-49.50, class 8 is 49.50-52.52, class 9 is 52.52-57.22, class 10 is 57.22-62.32, and class 11 is 62.32-398.73.
Figure 13.
Graphical result output of WoE analysis for the factor Rou. Class 1 is 0.00-8.93, class 2 is 8.93-16.53, class 3 is 16.53-24.95, class 4 is 24.95-28.88, class 5 is 28.88-40.73, class 6 is 40.73-44.33, class 7 is 44.33-49.50, class 8 is 49.50-52.52, class 9 is 52.52-57.22, class 10 is 57.22-62.32, and class 11 is 62.32-398.73.
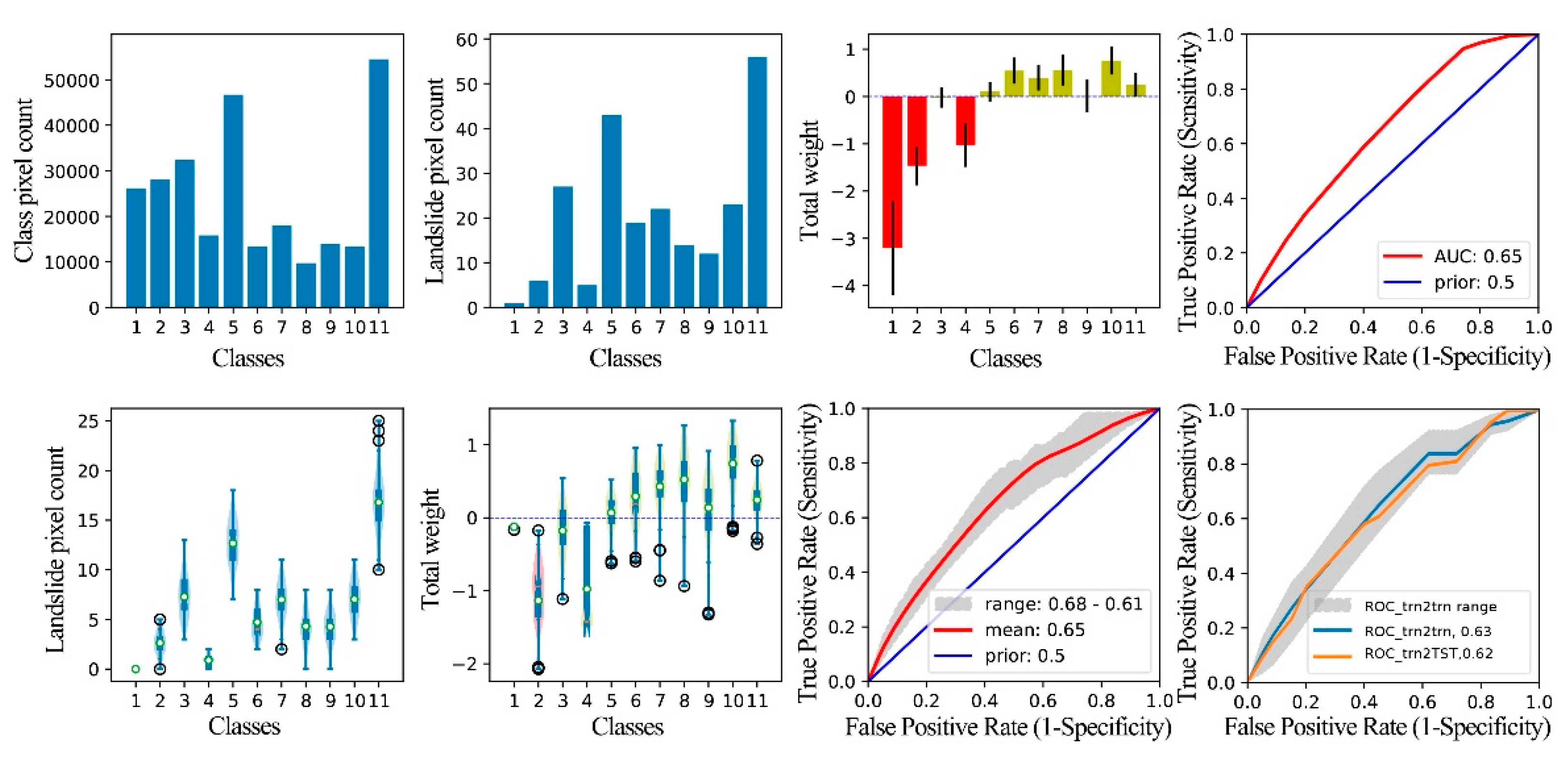
Figure 14.
Graphical result output of WoE analysis for the factor RSP. Class 1 is 0-0.01, class 2 is 0.01-0.02, class 3 is 0.02-0.05, class 4 is 0.05-0.06, class 5 is 0.06-0.08, class 6 is 0.08-0.14, class 7 is 0.14-0.29, class 8 is 0.29-0.45, and class 9 is 0.45-1.02.
Figure 14.
Graphical result output of WoE analysis for the factor RSP. Class 1 is 0-0.01, class 2 is 0.01-0.02, class 3 is 0.02-0.05, class 4 is 0.05-0.06, class 5 is 0.06-0.08, class 6 is 0.08-0.14, class 7 is 0.14-0.29, class 8 is 0.29-0.45, and class 9 is 0.45-1.02.
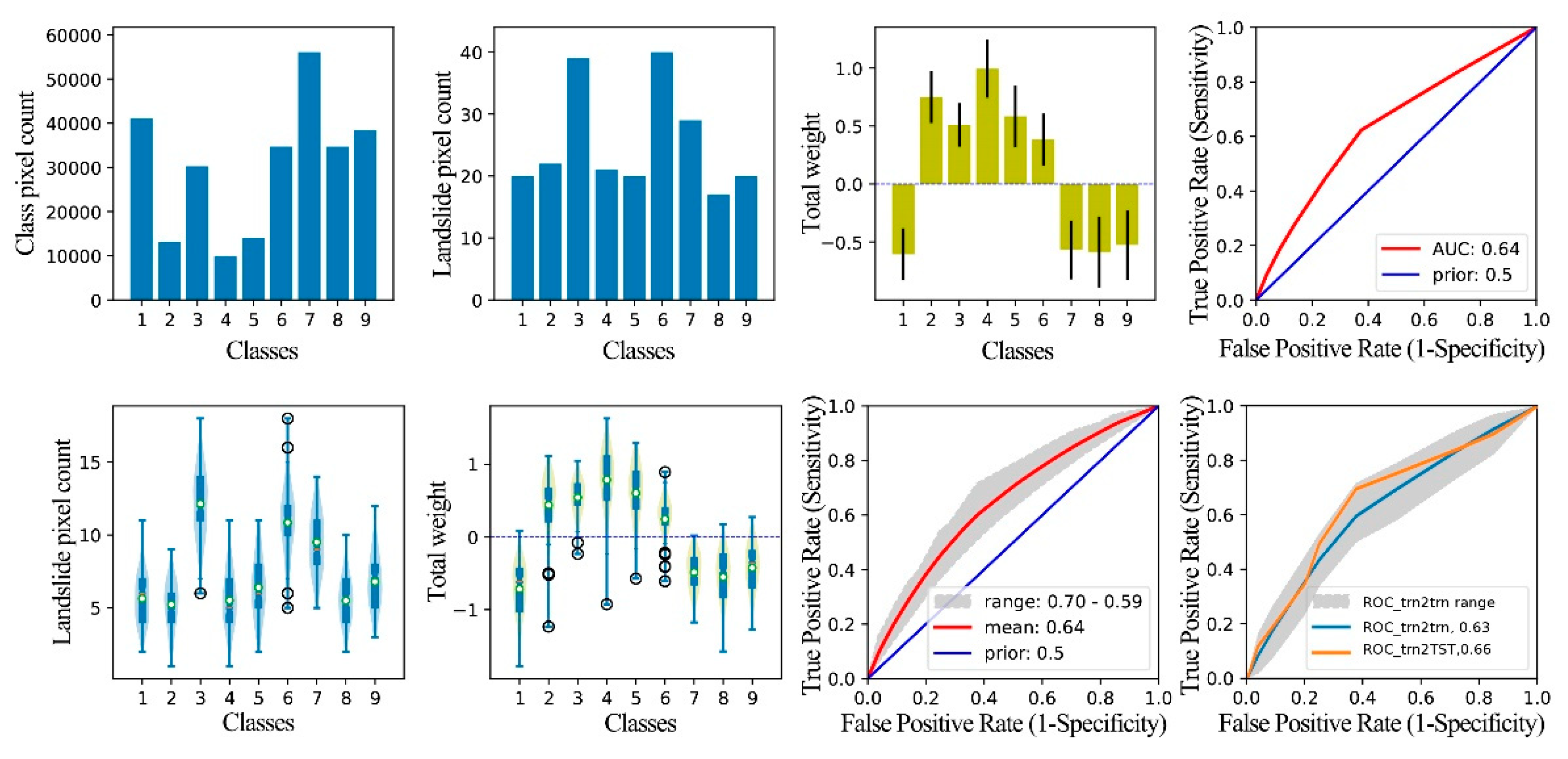
Figure 15.
Graphical result output of WoE analysis for the factor SL. Class1 is 0-4.12°, class3 is 6.44-7.65°, class5 is 10.83-11.65°, class6 is 11.65-16.13°, class8 is 17.12-21.10°, class10 is 25.60-28.27°, class11 is 28.27-39.98°, and class99 is other slopes.
Figure 15.
Graphical result output of WoE analysis for the factor SL. Class1 is 0-4.12°, class3 is 6.44-7.65°, class5 is 10.83-11.65°, class6 is 11.65-16.13°, class8 is 17.12-21.10°, class10 is 25.60-28.27°, class11 is 28.27-39.98°, and class99 is other slopes.
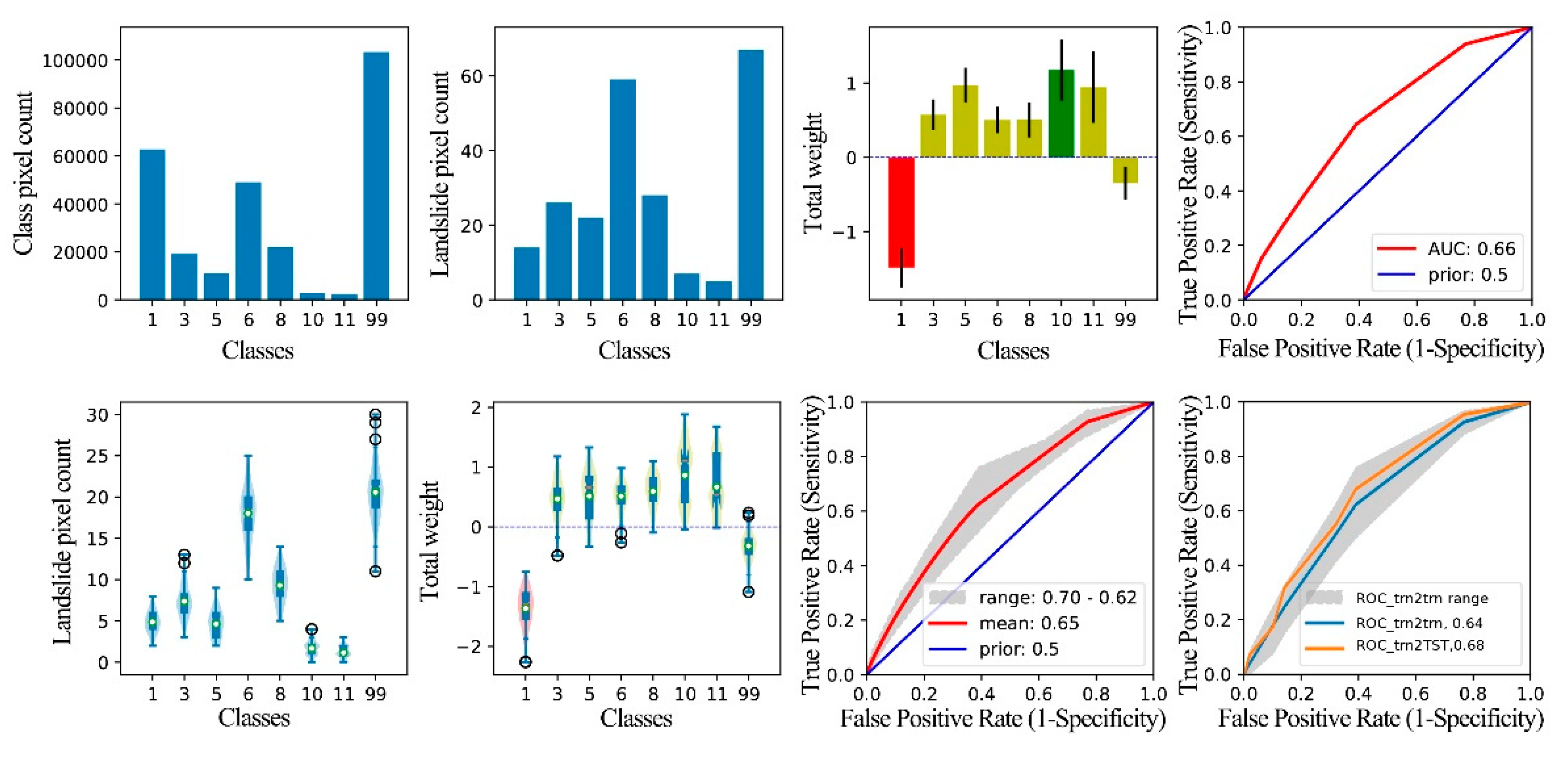
Figure 16.
Graphical result output of WoE analysis for the factor HANDH. Class 1~class 13 are divided by 0m, 38.06m, 49.60m, 65.22m, 100.45m, 115.44m, 184.98m, 1255.91m, 271.86m, 302.28m, 323.25m, 439.08m, 1176.82m, and 2831.14m.
Figure 16.
Graphical result output of WoE analysis for the factor HANDH. Class 1~class 13 are divided by 0m, 38.06m, 49.60m, 65.22m, 100.45m, 115.44m, 184.98m, 1255.91m, 271.86m, 302.28m, 323.25m, 439.08m, 1176.82m, and 2831.14m.
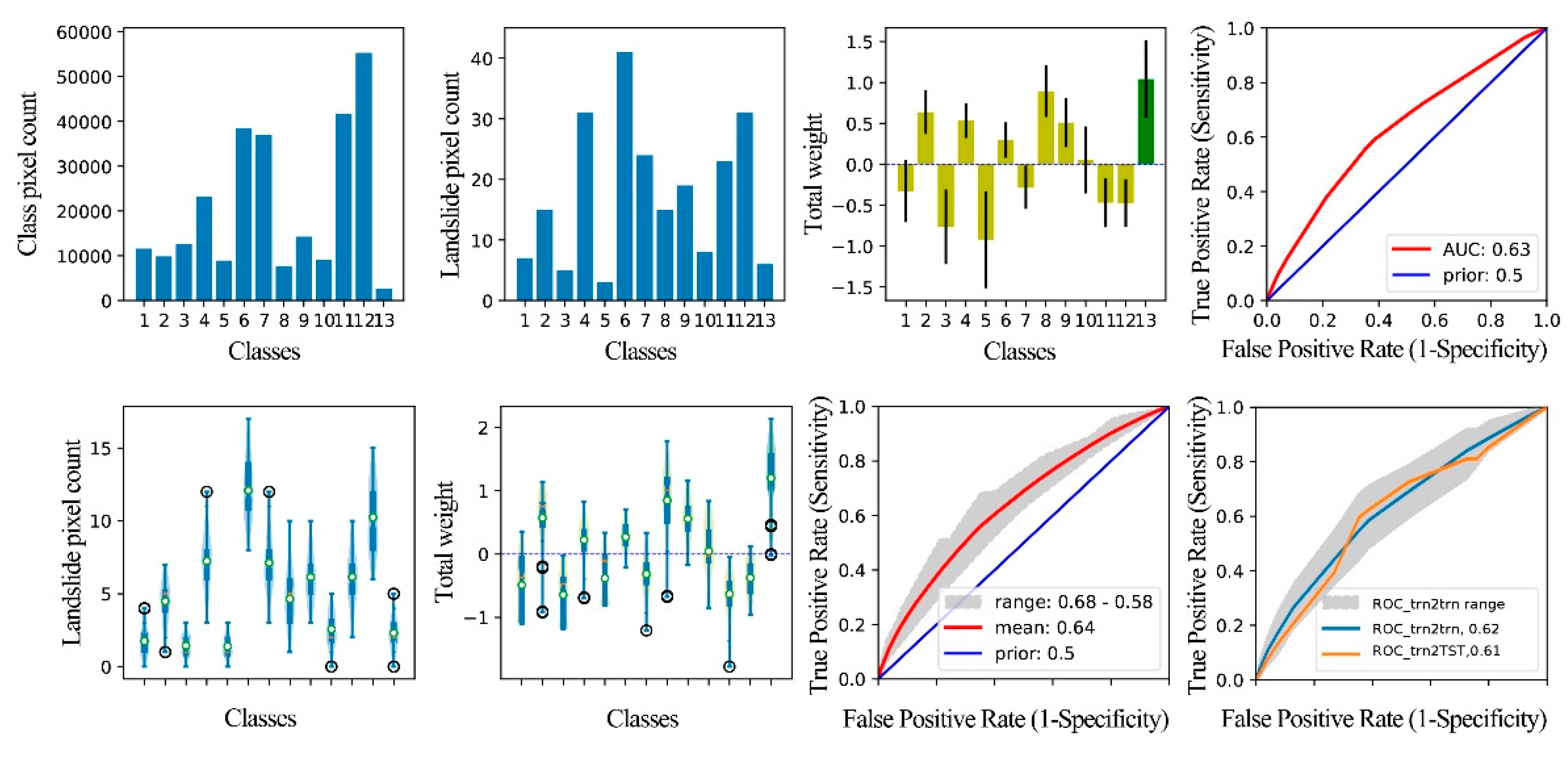
Figure 17.
Graphical result output of WoE analysis for the factor dCN. Class 1~class 14 are divided by 0m, 22.33m, 24.98m, 40.21m, 49.85m, 67.45m, 94.96m, 113.16m, 134.62m, 174.57m, 240.09m, 279.41m, 320.53m, 394.72m, and more than 394.72m.
Figure 17.
Graphical result output of WoE analysis for the factor dCN. Class 1~class 14 are divided by 0m, 22.33m, 24.98m, 40.21m, 49.85m, 67.45m, 94.96m, 113.16m, 134.62m, 174.57m, 240.09m, 279.41m, 320.53m, 394.72m, and more than 394.72m.
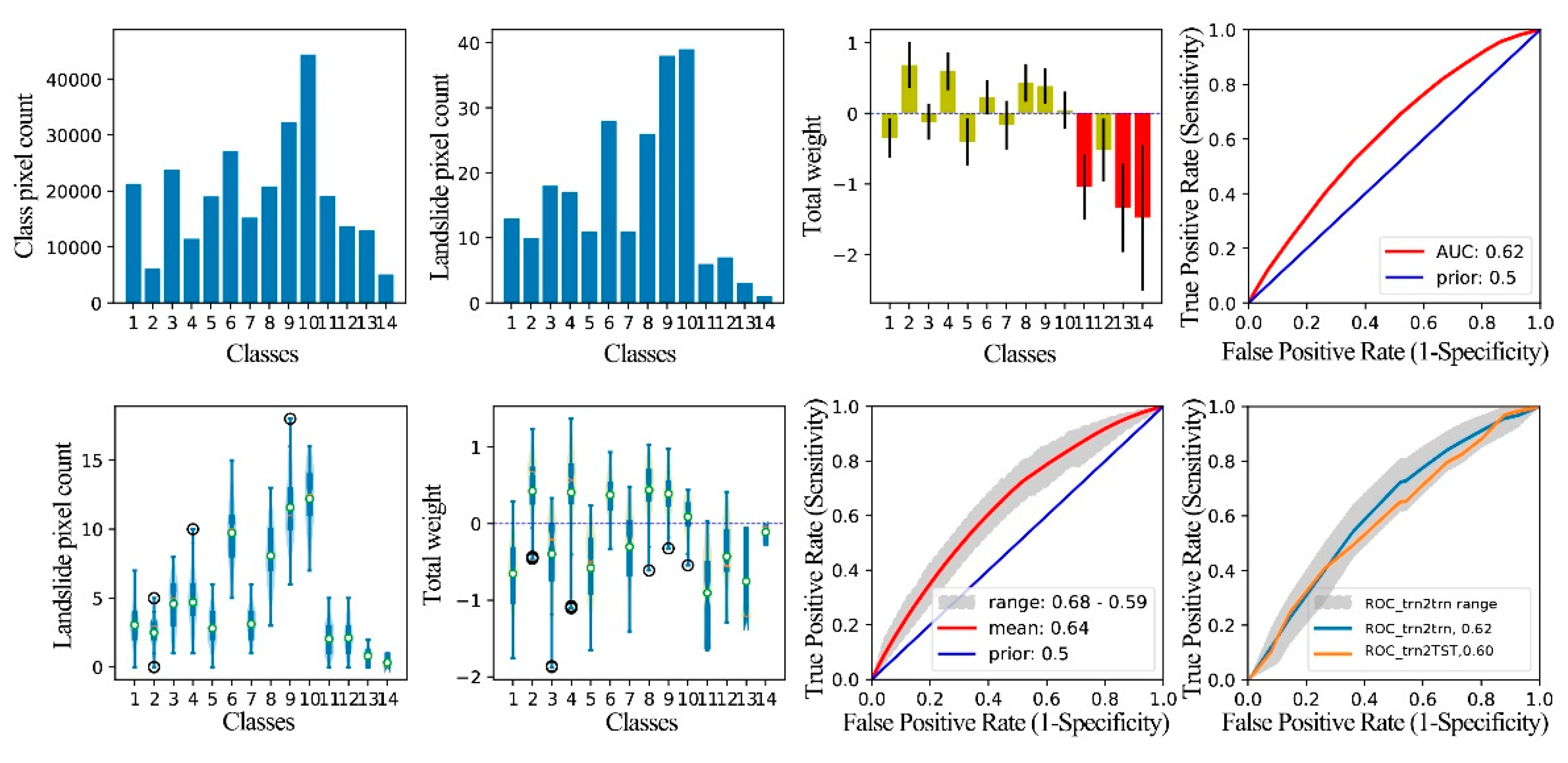
Figure 18.
Graphical result output of WoE analysis for the factor HANDV. Class 1~class 15 are divided by 0m, 4.15m, 6.93m, 13.03m, 15.61m, 17.89m, 24.11m, 26.22m, 34.53m, 37.77m, 41.57m, 55.48m, 66.60m, 77.37m, 101.59m, and 570.01m.
Figure 18.
Graphical result output of WoE analysis for the factor HANDV. Class 1~class 15 are divided by 0m, 4.15m, 6.93m, 13.03m, 15.61m, 17.89m, 24.11m, 26.22m, 34.53m, 37.77m, 41.57m, 55.48m, 66.60m, 77.37m, 101.59m, and 570.01m.
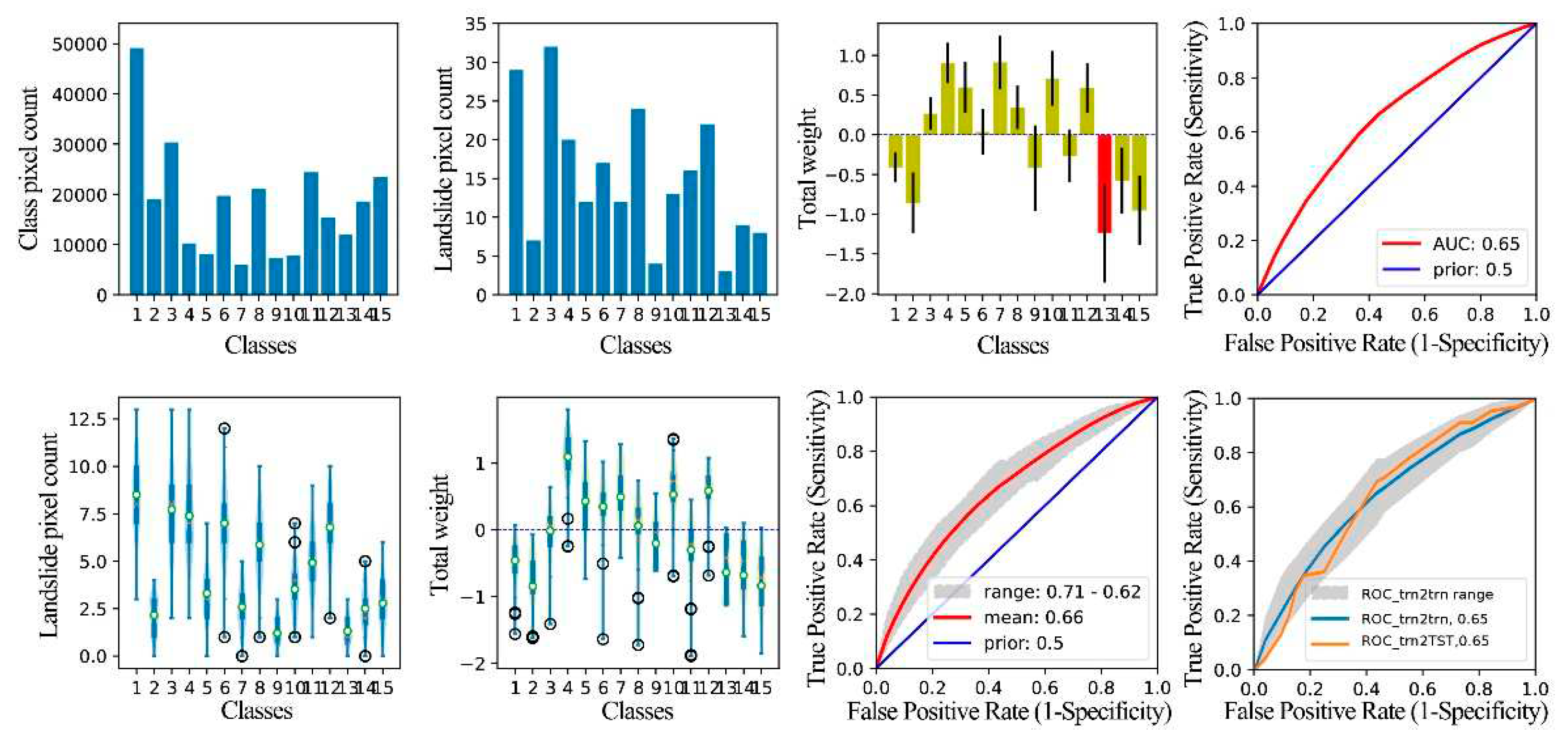
Figure 19.
Graphical result output of WoE analysis for the factor CLCD. Class 2 is forest, class 4 is grassland, and class 99 is others (cropland, shrub, barren, impervious, wetland).
Figure 19.
Graphical result output of WoE analysis for the factor CLCD. Class 2 is forest, class 4 is grassland, and class 99 is others (cropland, shrub, barren, impervious, wetland).
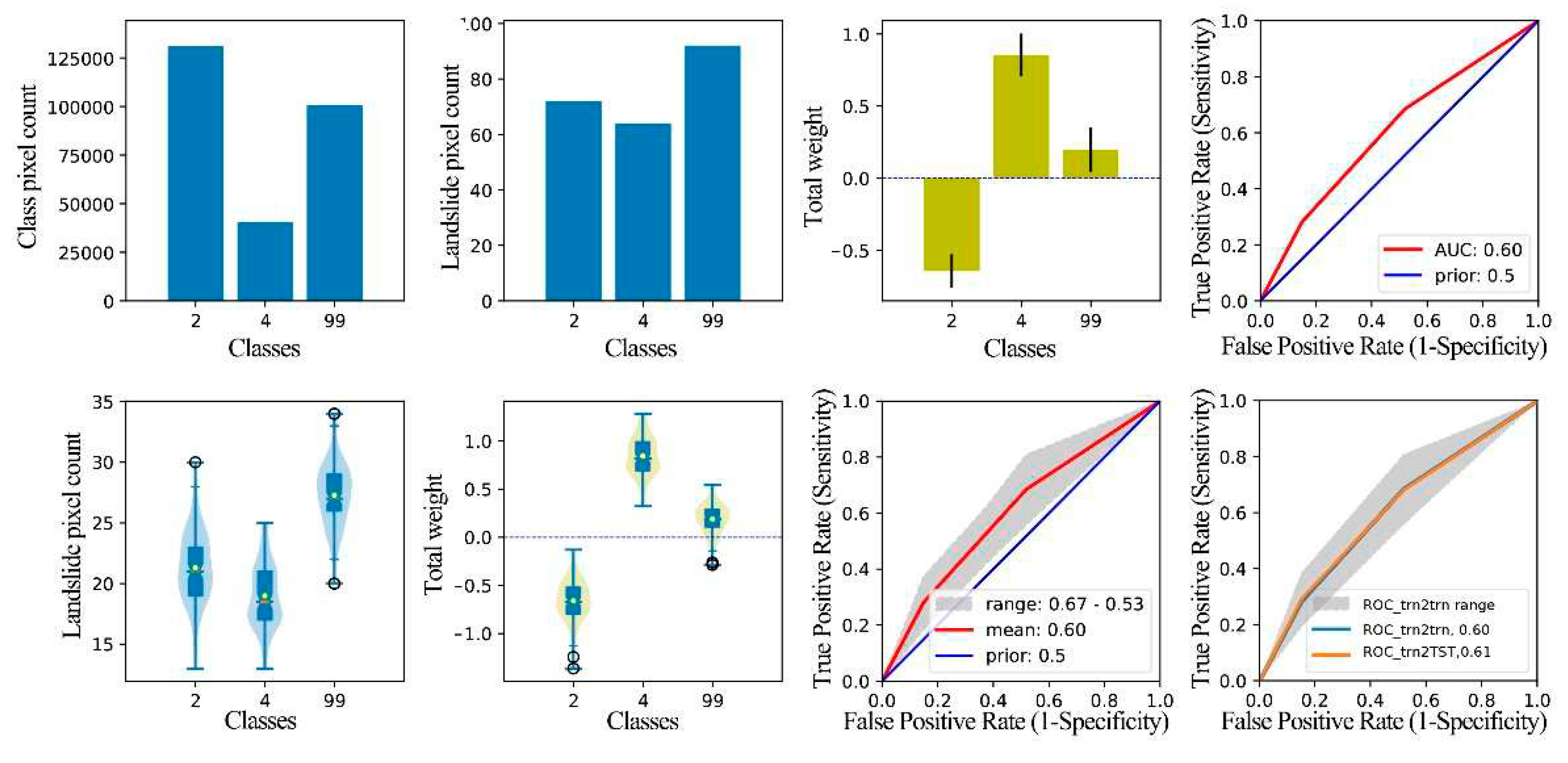
Figure 20.
Graphical result output of WoE analysis for the factor Cprof. Class 1 is -12611.46~-4084.50 (×10-6), class 2 is -4084.50~-2981.60 (×10-6), class 3 is -2981.60~-1533.30 (×10-6), class 4 is -1533.30~-973.62 (×10-6), class 5 is -973.62~-686.55 (×10-6), class 6 is -686.55~37.07 (×10-6), and class 7 is 37.07~10596.92(×10-6).
Figure 20.
Graphical result output of WoE analysis for the factor Cprof. Class 1 is -12611.46~-4084.50 (×10-6), class 2 is -4084.50~-2981.60 (×10-6), class 3 is -2981.60~-1533.30 (×10-6), class 4 is -1533.30~-973.62 (×10-6), class 5 is -973.62~-686.55 (×10-6), class 6 is -686.55~37.07 (×10-6), and class 7 is 37.07~10596.92(×10-6).
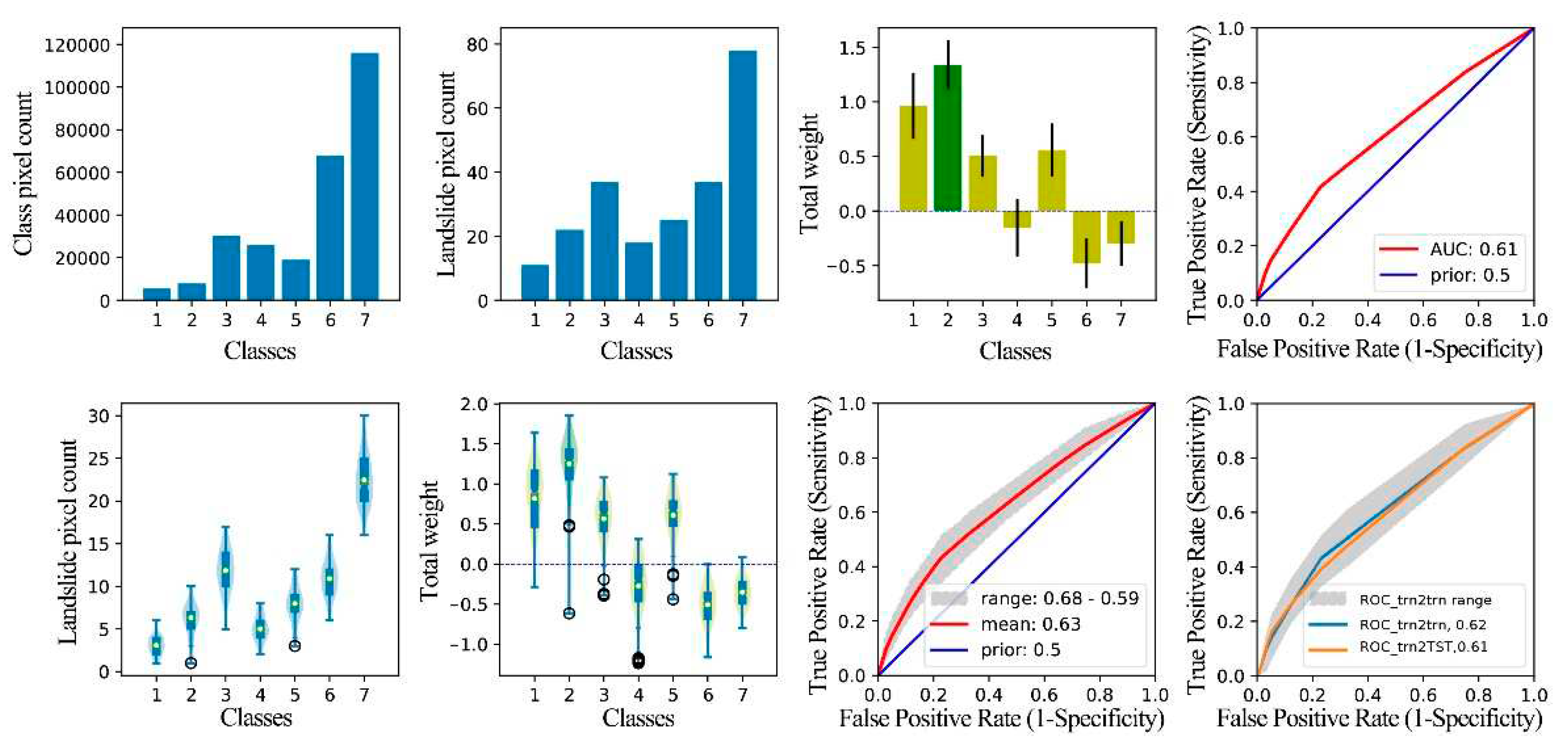
Figure 21.
Test results for conditional dependence. The upper right half represents the Pearson’s C results, and the factors with a strong correlation indicated by > 0.7 are determined by black circles, such as Rou and TRI (0.81), Rou and SL (0.71), and dCN and HANDH (0.82). The lower left presents the Cramer's V results.
Figure 21.
Test results for conditional dependence. The upper right half represents the Pearson’s C results, and the factors with a strong correlation indicated by > 0.7 are determined by black circles, such as Rou and TRI (0.81), Rou and SL (0.71), and dCN and HANDH (0.82). The lower left presents the Cramer's V results.
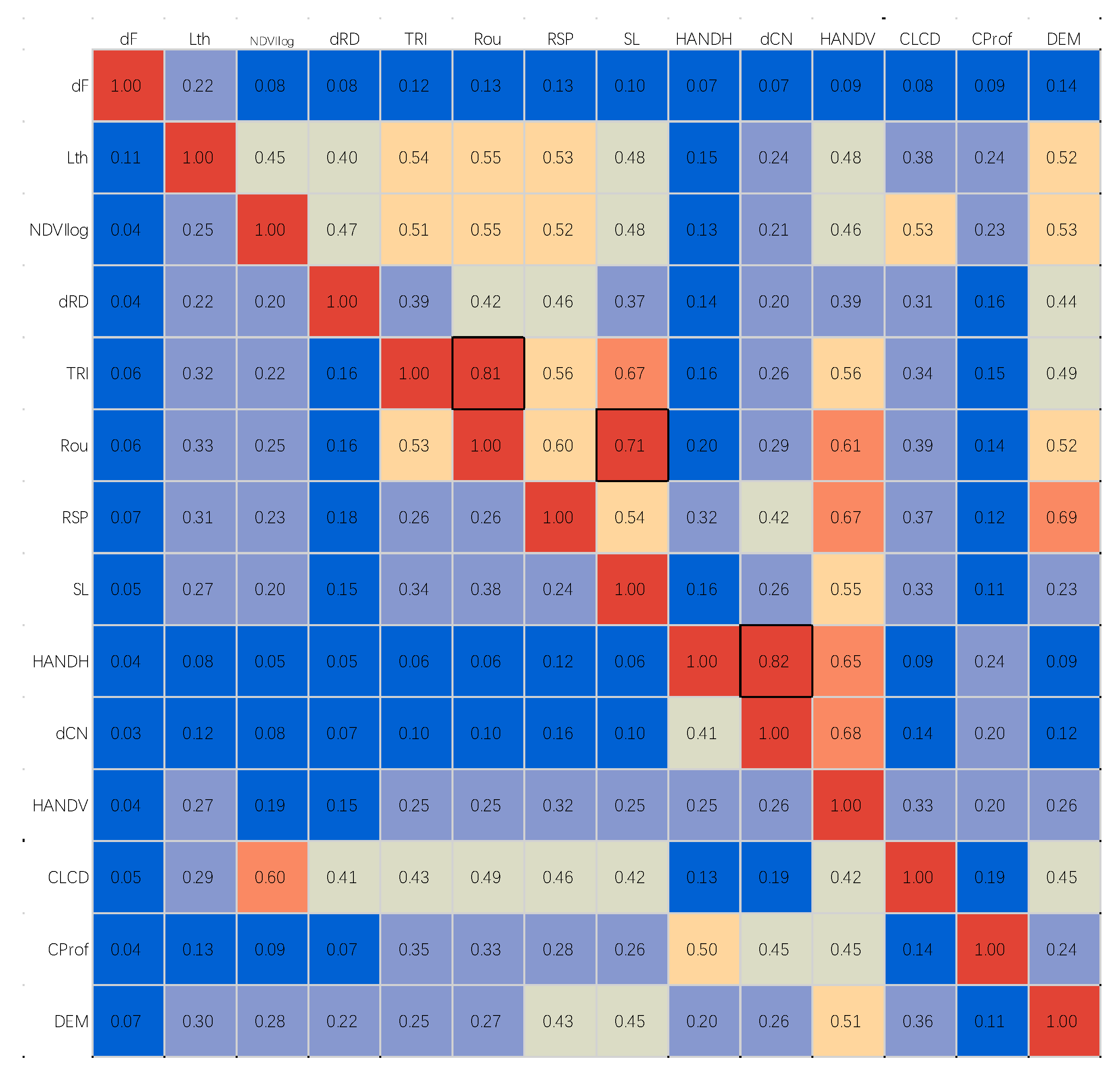
Figure 22.
Accuracy and validity assessment of the models. Accuracy assessment of the models of susceptibility to landslides with the ROC_trn2trn of models (The blue line and the grey range. The total weights for the models were based on trn and the performance of the models was evaluated using trn. One hundred iterations were carried out. The blue line is the mean ROC_M of 100 iterations. The grey range marks the model uncertainty based on the ROCs' MSE of 100 iterations.) Test of validity of the models with the ROC_M_trn2TST (the orange line). The total weight maps were based on the trn and the validation was assessed by using the TST.
Figure 22.
Accuracy and validity assessment of the models. Accuracy assessment of the models of susceptibility to landslides with the ROC_trn2trn of models (The blue line and the grey range. The total weights for the models were based on trn and the performance of the models was evaluated using trn. One hundred iterations were carried out. The blue line is the mean ROC_M of 100 iterations. The grey range marks the model uncertainty based on the ROCs' MSE of 100 iterations.) Test of validity of the models with the ROC_M_trn2TST (the orange line). The total weight maps were based on the trn and the validation was assessed by using the TST.
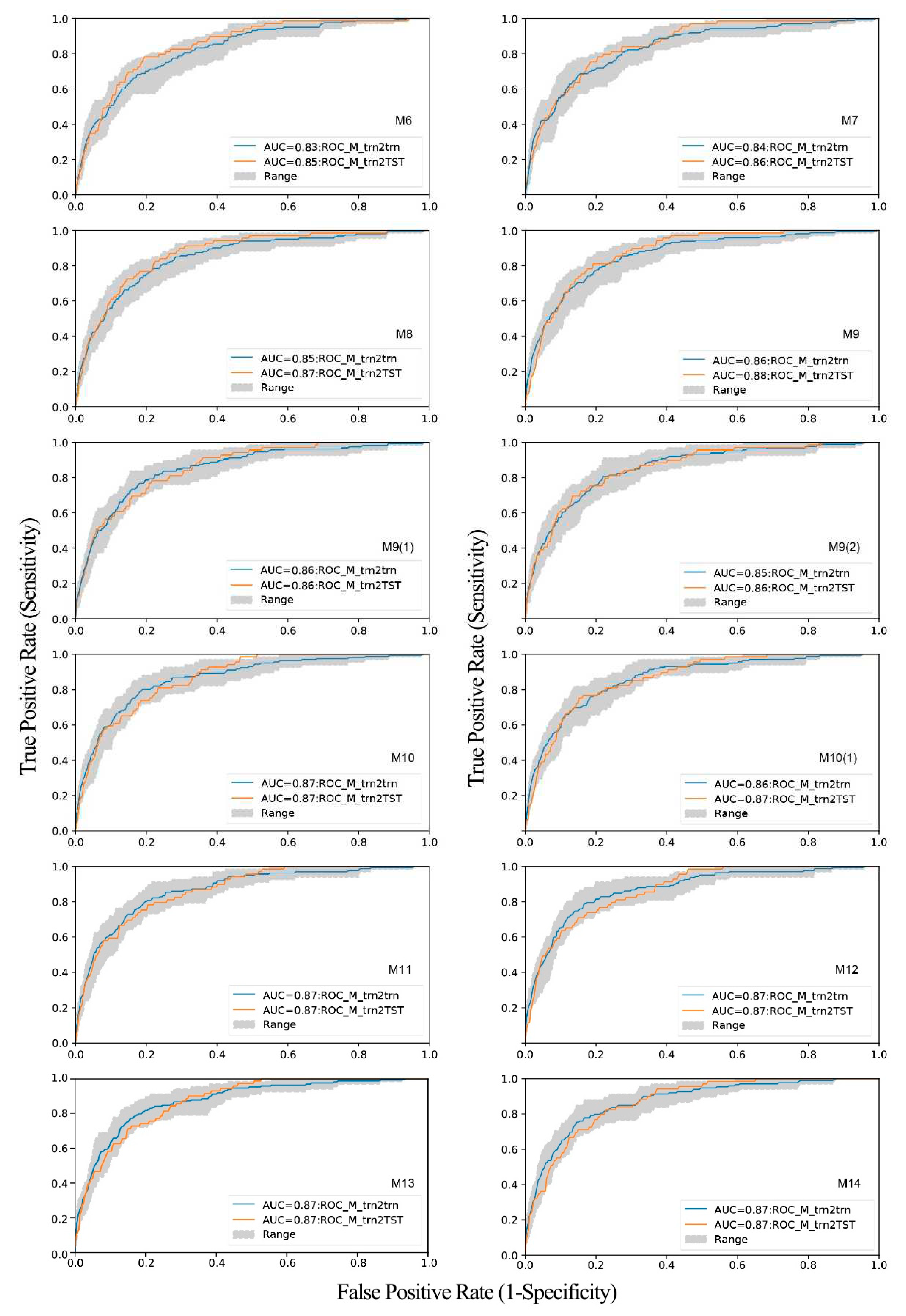
Figure 23.
Susceptibility map to landslides based on model M11 and trn. The model M11 has the highest rate of accuracy and validity. (a) and (b) are compiled using the same susceptibility partition data. The differences are as follows: (b) MS, LS and VLS use the same general gray color to highlight VHS and HS. VHS areas account for 5.05% of the study area and contain 50% of the total number of landslides. HS areas account for 14.53% of the study area and contain 30% of the total number of landslides. MS areas account for 28.23% of the study area and contain 15% of the total number of landslides. LS areas account for 32.55% of the study area and contain 4% of the total number of landslides. VLS areas account for 19.64% of the study area and contains 1% of the total number of landslides. The bottom picture is rendered using elevation and hill shade. The red ellipse roughly delineates the areas with high susceptibility and contiguous distribution.
Figure 23.
Susceptibility map to landslides based on model M11 and trn. The model M11 has the highest rate of accuracy and validity. (a) and (b) are compiled using the same susceptibility partition data. The differences are as follows: (b) MS, LS and VLS use the same general gray color to highlight VHS and HS. VHS areas account for 5.05% of the study area and contain 50% of the total number of landslides. HS areas account for 14.53% of the study area and contain 30% of the total number of landslides. MS areas account for 28.23% of the study area and contain 15% of the total number of landslides. LS areas account for 32.55% of the study area and contain 4% of the total number of landslides. VLS areas account for 19.64% of the study area and contains 1% of the total number of landslides. The bottom picture is rendered using elevation and hill shade. The red ellipse roughly delineates the areas with high susceptibility and contiguous distribution.
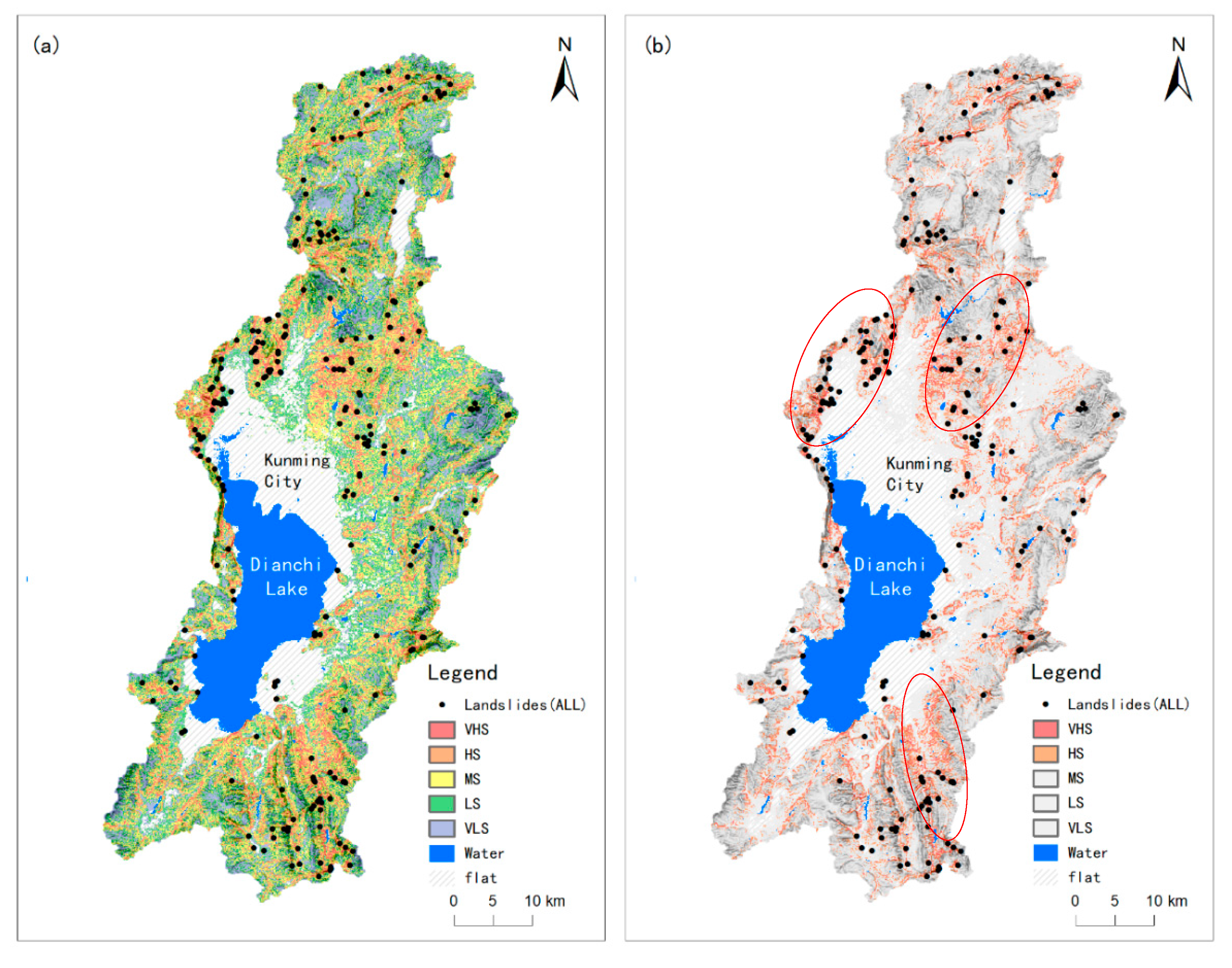
Table 1.
Sources and significances of the factors used in the analysis.
| No. | General category | Factors | Significance | Source and compilation method |
|---|---|---|---|---|
| 1 | Geologic | Distance to faults (dF) | Destruction of the stability of the rock mass structure | The fault structural lines came from the 1:200,000 geological map of Kunming. Using QGIS to compile Euclidean distance grid. |
| 2 | Lithology (Lth) | Lithological types of slope rock and soil | 1:200,000 geological map of Kunming | |
| 3 | Land cover | CLCD | The 30m annual land cover dataset in China | The 30m annual land cover dataset and its dynamics in China 2019 (CLCD) [19] |
| 4 | Land cover (LC) | The 10m land cover | ESA WorldCover 10 m 2020 v100 [28] | |
| 5 | Normalized difference vegetation index (NDVIlog) | China 30m Annual NDVI Maximum Dataset (2021) [29], as the log value. | ||
| 6 | Anthropogenic | Distance to roads (dRD) | Road cutting or vehicle vibration | Data come from OSM (OpenStreetMap, 2021). Using QGIS to compile the Euclidean distance grid. |
| 7 | Morphometric terrain parameters | Elevation (Elv) | Climate, vegetation and potential energy | NASADEM [30], the resolution of which is ~30m. |
| 8 | Aspect (Asp) | Solar insolation, flora and fauna distribution and abundance [1] | Compilation using SAGA GIS by NASADEM [30] | |
| 9 | Plan curvature (CPlan) | Converging, diverging flow, soil water content, and soil characteristics [1] | Compilation using SAGA GIS by NASADEM [30], with value ×106. | |
| 10 | Profile curvature (CProf) | Flow acceleration, erosion/deposition, and geomorphology [1] | Compilation using SAGA GIS by NASADEM [30], with value ×106. | |
| 11 | Tangential curvature (CTang) | Erosion/deposition [1] | Compilation using SAGA GIS by NASADEM [30], with value ×106. | |
| 12 | Topographic Position Index (TPI) | Quantifies topographic heterogeneity and erosion [31]. | Compilation using SAGA GIS by NASADEM [30] | |
| 13 | Terrain Ruggedness Index (TRI) | Quantifies topographic heterogeneity and erosion [32]. | Compilation using LSAT PM [4] by NASADEM [30] | |
| 14 | Roughness (Rou) | Quantifies topographic heterogeneity and erosion. | Compilation using LSAT PM [4] by NASADEM [30] | |
| 15 | Relative slope position (RSP) | Compilation using LSAT PM [4] by NASADEM [30] | ||
| 16 | Slope (SL) | Overland and sub-surface flow velocity [1] | Compilation using SAGA GIS by NASADEM [30] | |
| 17 | Water-related | Flow path length (FPL) | River erosion. | Compilation using SAGA GIS by NASADEM [30] |
| 18 | Flow Accumulation (FAlog) | Runoff velocity, runoff volume, and potential energy. | Compilation using SAGA GIS by NASADEM [30] as the log value. | |
| 19 | Height above nearest drainage (HAND) | River erosion, runoff velocity, runoff volume, and potential energy [33,34]. | Compilation using SAGA GIS by NASADEM [30] | |
| 20 | Horizontal HAND (HANDH) | River erosion, runoff velocity, runoff volume, and potential energy [33,34]. | Compilation using SAGA GIS by NASADEM [30] | |
| 21 | Vertical HAND (HANDV) | River erosion, runoff velocity, runoff volume, and potential energy [33,34]. | Compilation using SAGA GIS by NASADEM [30] | |
| 22 | Distance to channel network (dCN) | River erosion. | Compilation using SAGA GIS by NASADEM [30] | |
| 23 | Stream power index (SPIlog) | River erosion [35]. | Compilation using SAGA GIS by NASADEM [30] as the log value. | |
| 24 | Topographic wetness index (TWI) | Moisture content of soil [35,36,37] | Compilation using SAGA GIS by NASADEM [30] | |
| 25 | SAGA Wetness Index (TWISAGA) | Moisture content of soil [37,38] | Compilation using SAGA GIS by NASADEM [30] |
Table 3.
Statistical table of landslide susceptibility zoning area.
| Sub-regions | Area of sub-regions (%) | Total area of sub-regions (%) | Landslides(%) | Total landslides(%) |
|---|---|---|---|---|
| VHS | 5.05 | 5.05 | 50 | 50 |
| HS | 14.53 | 19.58 | 30 | 80 |
| MS | 28.23 | 47.81 | 15 | 95 |
| LS | 32.55 | 80.36 | 4 | 99 |
| VLS | 19.64 | 100 | 1 | 100 |
Table 4.
Thirteen factors with AUCs≥0.6 and their AUC values.
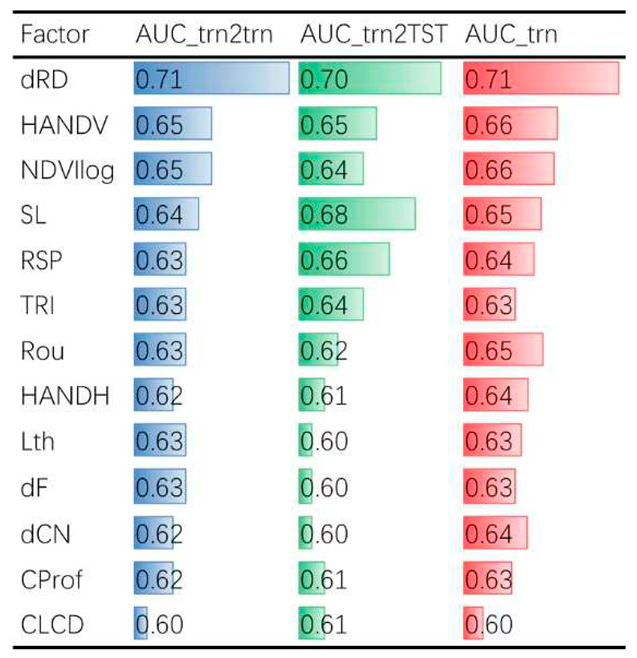
Table 5.
Factor classification with W+ ≥ 0.5
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Submitted:
25 August 2023
Posted:
25 August 2023
You are already at the latest version
Alerts
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
25 August 2023
Posted:
25 August 2023
You are already at the latest version
Alerts
Abstract
The nine plateau lake watersheds in Yunnan are important ecological security barriers for southwest China, and the prevention and control of landslides are important considerations in the management of these watersheds. Taking Dianchi Lake watershed as a typical study area, this paper puts forward an improved comprehensive process of landslide susceptibility evalua-tion, and discusses the model’s sensitivity regarding susceptibility to landslides. The compre-hensive process is based on the weight of evidence method (WoE) and integrates many analyti-cal techniques, such as cross-validation, multi-quantile cumulative Student’s comprehensive weight analysis, independence tests, step-by-step modeling, ROC analysis and ROC-based sus-ceptibility zoning. This paper established fourteen models, with high accuracy and validity AUC, reaching 0.83-0.87 and 0.85-0.88, respectively. Moreover, according to the susceptibility zoning map compiled using the optimal model, 80% of landslides can be predicted in the very high and high susceptibility zones, which only account for 19.58% of the study area. Finally, the strategies for geological disaster prevention and ecological restoration deployment were put forward, providing great guiding significance for deeply understanding the landslide susceptibility of lake watersheds (Dianchi Lake) in Yunnan Plateau and guiding the planning and deployment of landslide prevention and mitigation activities and ecological restoration in the watershed.
Keywords:
Subject: Environmental and Earth Sciences - Geophysics and Geology
1. Introduction
Yunnan province is an important ecological security barrier in southwest China, and lakes are important ecological areas. The government of Yunnan province is promoting the ecological protection and restoration of nine plateau lake watersheds (Figure 1), and landslide disaster prevention is one of the important goals of these activities. In order to support this ongoing project, it is necessary to evaluate landslide susceptibility, taking lake watershed as the unit, establish the geological environment and human activity factors that may affect or control landslide susceptibility in the watershed, understand the distribution of landslide susceptibility in the watershed, and guide the formulation of targeted prevention and control countermeasures. Dianchi Lake is the largest of the nine plateau lakes in Yunnan, and Kunming city is in this watershed, where human engineering activities are relatively strong, and so it is reasonable to choose Dianchi Lake watershed as the research area.
Landslides in plateau mountainous areas are always a problem, because they affect people's lives, destroy the land surface and cause economic losses [1]. Identifying the dangerous areas related to landslides is an important part of disaster management [2], and it is also an important basis for promoting human safety, infrastructure development and ecological environment protection in these mountainous areas [1]. Landslide susceptibility analysis (LSA) describes the spatial probability of landslides [3,4]. On the regional scale, the modeling method of landslide susceptibility based on statistics is considered appropriate [2,5,6,7]. We used the Weight of Evidence (WoE) method [8] to complete this analysis, which is a statistical-based method and also represents an intermediate and complex data-driven method [9]. Although WoE is a bivariate statistical method frequently used in LSA in recent decades [1,2,6,7,9,10,11,12,13,14,15,16], establishing how to optimize the modeling process to improve the accuracy and validation of the model is a problem worth exploring. In addition, because WoE only uses discrete data, continuous raster data need to be classified, but there is no standardized method of factor data classification, which is another problem worth exploring [2,4,8].
This study focuses on LSA and landslide susceptibility mapping (LSM) in the Dianchi Lake watershed of Yunnan Plateau, which has important ecological barrier significance. This method has outstanding application value, aiming at strengthening the ability to assess the susceptibility risk of landslide disasters and improving the corresponding consulting services for stakeholders related to disaster reduction. In terms of research content, on the one hand, the characteristics of sensitive factors of landslide susceptibility were clarified; on the other hand, the spatial distribution of landslide susceptibility was clarified, which provides important technical support for guiding ecological restoration and geological disaster prevention and mitigation deployment in plateau lake watersheds. In terms of technology, this paper puts forward an improved comprehensive process of landslide susceptibility evaluation based on the WoE method, including: (1) data preparation; (2) optimizing the compilation of datasets for factor classification based on cumulative Student’s comprehensive weight (sC) curve and WoE statistics; (3) screening modeling factors based on the cross-validation theory and AUC factor indicators; (4) step-by-step modeling to optimize high-performance models; and (5) dividing landslide susceptibility zones base on ROC. In this paper, the improved analysis process was applied to obtain the results of the WoE landslide susceptibility model with excellent fitting performance and prediction performance (both AUC reached 0.87), and the spatial distribution map of landslide susceptibility classification in the study area was compiled, and the strategies of geological disaster prevention and ecological restoration deployment were put forward, which is of great guiding significance for deeply understanding the landslide susceptibility of lake watersheds (Dianchi Lake) in Yunnan Plateau and guiding the planning and deployment of landslide prevention and mitigation and ecological restoration in the watershed.
2. Study Area and Data
2.1. Study Area
The study area is bounded by the watershed of Dianchi Lake watershed (Figure 1), with an area of 2906.44km2. The water surface of Dianchi Lake and reservoir, the center of Kunming basin, the sub-basins and some flat hilltops are not prone to landslides. Therefore, based on the landform results of DEM classification [17,18], deducting 700.15km2 of the "flat" category, the actual analysis area in this paper was 2206.29km2. This area is a lake basin and mountainous terrain in the middle of Yunnan Plateau, with Dianchi Lake’s waters and basins in the south-central part, rugged mountains in the north, east and south, and Xishan mountain in the west, with steep fault cliffs. The elevation of this area ranges from 1896m at the surface of Dianchi Lake to about 2800m in the mountainous area, with a height difference of more than 900m. The steep mountain terrain around the basin, the continuous and rapid cutting of rivers, the heavy rainfall in the rainy season and the man-made influence caused by the downward cutting of slopes during road construction make the area prone to slope failure.
2.2. Landslides Dates and Data Preparation Based on Random Sampling
The study area has a good working history in landslide survey, and it is the key monitoring and prevention area of landslides in Yunnan Province. Through field investigation, the list of historical landslides was checked and revised, and a total number of 228 landslides were included in the list of landslides analyzed in this paper (Figure 1).
We adopted the cross-validation technique, the basic technique used to evaluate the uncertainty of statistics and models by using test datasets that do not involve model training [4,20,21], to prepare the data. Figure 2 briefly summarizes the compilation process of the landslide dataset: (1) we divide all landslide data (ALL) into a training dataset (TRN) containing 158 landslides and a test dataset (TST) containing 70 landslides by using random sampling tools, and TRN and TST were not duplicated. The former and the latter corresponded to about 70% and 30% of ALL, respectively. TRN was used to calibrate the model and TST was used to evaluate the performance of the model. (2) In order to estimate the model variables that depend on the sample size, we used the random sampling tool to generate 100 random sub-samples with TST size from TRN, and some landslides in different random sub-samples were allowed to be repeated, forming a training data subset trn.
2.3. Factor Data
According to the characteristics of the study area, data availability and previous studies, the landslide control factors can be roughly divided into different groups [6,15]; the compiled landslide control factors are listed in Table 1. At first, we did not rule out the available or main factors that are easy to deduce, because these factors may help to explain the landslide susceptibility in the study area. These factors have been used in other studies, and descriptions of these factors can be found in a large number of studies [2,15,22,23,24,25,26], so this article did not elaborate upon this further. Because landslides usually do not happen by accident, they are unevenly distributed in different factors and factor classifications [2,27]; we thus used the method in Section 3.3 to statistically evaluate the relationship between landslide occurrence and spatial distribution of some factors based on single-factor WoE statistics.
3. Methods
3.1. Weights-of-Evidence Method (WoE)
The WoE method is a well-known and widely used bivariate statistical method which is used to estimate the relationship between observation data (landslide training inventory) and potential control factors (geological and geomorphological factors) [8,39]. A single factor’s weight is superimposed on the linear model to obtain the overall landslide susceptibility model [1,8,11,39]. It was first introduced in the late 1980s for the application of GIS-based geological science, mainly to assist the mapping of mineral potential [8,39,40,41,42]. Later, this method was widely used in LSM [1,2,6,7,10,11,12,13,14,15,16].
is defined as the unit with geological disasters, is defined as the unit without geological disasters, is defined as the unit in the evidence factor area, is defined as the unit outside the evidence factor area, is defined as the conditional probability symbol, and is defined as the number of grid pixels. WofE considers two weights and posterior probability[2,6,8,15,39,41,42]:
The weight symbols and do not represent the mathematical meaning of numerical values, but rather represent the presence (positive) and absence (negative) of feature classes in a given raster cell. According to the above formula, a positive logic value indicates the positive influence of a given variable, a negative logic value indicates the negative influence, and a logic value of zero indicates no influence.
The posterior probability is an indicator of susceptibility, with a higher value indicating higher susceptibility, and a lower value indicating lower susceptibility. The formula for calculating the posterior probability is: , , , where: is “+” when the -th evidence factor layer exists, an is “-“ when it does not exist; is the weight of the existence or non-existence of the -th evidence factor.
In order to evaluate the spatial correlation strength between single factors and landslide and the performance of the model, this paper used the receiver operating characteristic curve (ROC) algorithm, which is a technique to visualize and evaluate the classifier performance by describing the ratio of the true positive rate (sensitivity) to false positive rate (1-specificity) [43]. The area under the ROC curve (AUC) provides a quantitative index to compare the advantages and disadvantages.
3.2. Main Analysis Process
In this paper, an improved evaluation process of landslide susceptibility based on WoE is proposed, which mainly includes: (1) data preparation, (2) optimizing the compilation of datasets for factor classification, (3) screening modeling factors, (4) gradually adding factor modeling to optimize high-performance models, and (5) dividing landslide susceptibility level zones.
(1) Data preparation. Clean up the landslide inventory, and compile the training set (TRN), test set (TST) and training set subset (trn) by using cross-validation technology (see Section 2.2 for details). Prepare the initial dataset of factors (see Section 2.3 for details).
(2) Optimizing the compilation of datasets for factor classification. In this paper, a sub-process of optimizing factor classification is proposed to process the initial dataset of factors to obtain excellent classification dataset. See Section 3.4 for the introduction of this method.
(3) Screening modeling factors. Firstly, according to the single factor WoE statistical results, the factors of low AUCs (this paper chooses AUC < 0.59) are excluded. Secondly, exclude the factors with high correlation. The use of strongly correlated datasets may lead to incorrect estimation of factor contribution and expansion of estimated probability value [44]. Chi-square-based contingency analysis is performed on the classified data based on the raster [4,15], according to Pearson's C and Cramer's V, to measure the correlation between discrete datasets.
(4) Step-by-step modeling, and optimizing the high-performance model. According to AUCs and correlation statistical indicators obtained using single-factor WoE statistics, the factors are sorted and combined. The model is based on the factor composition with high AUCs. Then, try to add follow-up factors into the new model in turn, and recalculate and evaluate the ROC_M curve and AUC_M index of the new model. Evaluate the fitting performance and uncertainty of the model. The range and average ROC curves (ROC_M_trn2trn) and AUC (AUC_M_trn2trn) of 100 sensitivity model results are obtained by fitting trn with the model based on the average weight calculated by trn. After this, evaluate the prediction performance of the model. The ROC curve (ROC_M_trn2TST) and AUC (AUC_M_trn2TST) are obtained by fitting TST with the model based on the average weight calculated by trn. Use the above ROC_M and AUC_M indicators to evaluate whether and how the model benefits from the last added factor, and discard the factors that cannot improve the AUC_M indicators of the model or improve the ROC_M consistency.
Figure 3.
Flow chart of the improved WoE landslide susceptibility assessment.

(5) Landslide susceptibility zoning based on ROC_M. Adopt a zoning method to improve the readability of the landslide susceptibility map. This method uses the success rate to describe that the cumulative landslide area exceeds the cumulative area that is considered vulnerable [45]. In the ROC curve, the Y-axis representing the true positive rate corresponds to the cumulative landslide area, and the X-axis representing the false positive rate describes the cumulative research area without landslide area, which is regarded as an area that is susceptible but does not include landslide area, and is an approximation of the total research area. There is no established standard for the definition of the partition threshold. In this paper, we used 50% of all landslide pixels to represent very-high-susceptibility areas (VHS), which means that an aggregated susceptible area contains 50% of the detected landslide areas. Assuming that the location of future events will follow the drawn susceptibility model, we can also assume that about 50% of all future landslide areas will also be located in this area. We used values of 30% for high-susceptibility areas (HS), 15% for medium-susceptibility areas (MS), 4% for low-susceptibility areas (LS), and about 1% for very-low-susceptibility areas (VLS). Therefore, the first two areas (VHS and HS) include about 80% of the known landslide areas.
3.3. WoE Statistic Process
Using cross-validation technology, with single-factor classification data, ALL, trn and TST, according to the WoE method, the regional distribution of discrete class factors, the corresponding landslide pixel frequency, weight, variance, ROC and AUC in these classes are counted. The output data include ten items: WoE_ALL, sC_ALL, WoE_trn, sC_trn, AUC_ALL, AUC_trn, ROC_trn2trn, AUC_trn2trn, ROC_trn2TST, and AUC_trn2TST, where WoE_ALL, sC_ALL and AUC_ALL are the weight, sC and AUC calculated based on ALL, respectively; WoE_trn, sC_trn, and AUC_trn are the mean weight, sC and AUC calculated 100 times based on trn, respectively; ROC_trn2trn and AUC_trn2trn are the single-factor accuracy assessment indexes modeled by single-factor weight WoE_trn and fit to trn; and ROC_trn2TST and AUC_trn2TST are the single-factor validity assessment indexes modeled by single-factor weight WoE_trn and fit to TST.
Figure 4.
Process flow chart of single factor WoE statistic.

Because landslides usually do not happen by accident [4,6,27], one can statistically evaluate the relationship between landslides and the spatial occurrence of some parameters based on the above single-factor WoE statistics. In this paper, trn (containing 100 subsets) was used for statistics, and the statistical process was repeated 100 times for each control factor. Calculate the mean weight of each factor category (WoE_trn) and its corresponding statistical values, such as variance and standard deviation. ROC is used to graphically evaluate the classification ability of each factor for each statistic. This statistical process has two advantages [6]. Firstly, based on its estimated variance, it can better represent the general uncertainty of the sensitivity model; Secondly, for classified data, it can be determined whether the significant weight has accidental characteristics or whether it can be reproduced from different random samples, which is more likely to be causal.
Use trn to evaluate the accuracy performance of the model and use TST to evaluate the validation performance of the model for new data prediction [7,16]. If the ROC curve based on TST falls within the ROC curve range based on trn (representing MSE), it shows that the accuracy and validation of the model can be good; if not, the model may be over-fitted.
Figure 5.
Process flow chart of accuracy and validation assessment of models.

3.4. Optimization Process of Single Factor Classification
Because WoE uses discrete data, it is necessary to classify continuous single factor data discretely, which will lead to the discontinuity of factor weights. The traditional single-factor discrete classification number and classification threshold determination is subjective. In this paper, a single factor classification optimization process (Figure 6) is proposed, and the main steps are as follows:
Firstly, generate the cumulative sC curve. This method involves subdividing the continuous numerical single-factor raster into classes according to the quantile and calculating its weight and corresponding variance for each class. The difference between the two weights—that is, the comprehensive weight—the quantitative evidence factor and the correlation between geological disasters are calculated as follows [39]: . If is positive, the evidence factor is favorable to geological disasters, while if it is negative, it is unfavorable to landslides. If is close to zero, it shows that the evidence factor has little to do with geological disasters. A confidence measure defined by contrast divided by its standard deviation is introduced, which is similar to Student’s comprehensive weight sC. The sC is relatively large when the standard deviation is small, so the results are more reliable. When the test values of sC are 1.96 and 2.326, the confidence is 97.5% and 99% [8,39,41]. , , , where 、 and are standard deviations of , and , respectively. Use the accumulated sC to define a new discrete distance category [6]. As long as the weight value is positive, the sC should be increased; when the weight value is close to zero, it should be flattened; and when the weight value is negative, it should be reduced. Therefore, the shape of the cumulative sC curve is expected to show its maximum value at the position of its maximum expected influence. If there is more than one maximum, it indicates the distortion effect of another variable [6].
In this step, we put forward an improved technical subprocess: using the results of multiple quantile calculations for comprehensive analysis—that is, compiling a series of cumulative sC curves of quantile statistics at the same time. This will help to show the changing trend of cumulative sC more comprehensively and capture the possible segmentation threshold. First, it can guide the selection of segmentation threshold and reduce the subjectivity of segmentation threshold setting. Secondly, it can reveal the sensitivity of factor values to landslides in a single-factor segment, and also maintain the continuity of the weight trend well, and improve the discrimination of landslide sensitivity of each influencing factor.
Set the threshold of classification and segmentation based on the cumulative sC curve, re-classify the factors, and perform single factor WoE statistics on the re-classified factor data (Section 3.3).
Then, set a new trial segmentation threshold and repeat the above steps.
Finally, we propose determining the best classification based on two criteria (Criterion 1 and Criterion 2). Criterion 1: Division or merger, is it beneficial to (1) eliminate classifications of continuous sC<2; (2) reduce classifications of sC<2; (3) increase classifications of sC>2; or (4) increase the value of AUCs? After several rounds of trial calculation, the optimal classification is determined according to Criterion 2: Select the best categorization with (1) the highest AUCs; (2) better fitting between ROC_trn2TST and ROC_trn2trn; and (3) more classes with sC>2.
4. Results
4.1. Cumulative sC Statistical Curve of Continuous Single Factor
In this study, the landslide dataset ALL was used to count the continuous numerical factors by using the statistical method proposed in Section 3.4. In order to obtain the statistical curves after classification with different quantiles, we draw the frequency distribution of the original data of factors and the cumulative sC statistical curves of six quantiles of 100, 80, 60, 40, 20 and 10 (Figure 7), which reveals the correlation between continuous numerical factors and the spatial distribution of landslides in different quantiles in detail, not only reflecting the changing trend of cumulative sC, but also showing the details of the changes in cumulative sC. These cumulative sC curves are a reference to guide the selection of classification thresholds. In this study, after several rounds of trial calculation, we summarized the following experiences in setting classification thresholds: (1) at the maximum peak and minimum valley, (2) more classification thresholds can be set for curves with steep slopes, (3) the secondary peak (valley) values of curves drawn using different quantiles can be tested as classification thresholds, but only the peak (valley) values of curves drawn using individual quantiles should be selected as classification thresholds. (4) The more classification items with sC>2, the better. (5) The fewer the total classification items in the classification results, the better. (6) The larger the three AUCs (AUC_ALL, AUC_trn and AUC_TST), the better. (7) ROC_trn and ROC_TST should be coordinated (ROC_TST is within the range of ROC_trn).
4.2. Results of Single Factor WoE Analysis
After implementing the technical processes in Section 3.4 and 3.3, we obtained the evidence weight and sensitivity strength analysis results of each factor (Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19 and Figure 20). The results are shown in eight pictures. In the first line, the first picture presents the statistics of the number of grids in each category of factors; The second picture shows the distribution of all landslide data in each factor classification; The third picture is a C histogram of factor classification based on all landslide data statistics, and the black vertical line is the error bar of C; and the fourth picture presents the ROC_ALL and AUC_ALL based on all landslide data statistics. In the second line, the first picture is a violin-box diagram based on 100 subsets of trn and counting the distribution of landslide data 100 times in each factor classification; the second picture is a C violin-box diagram of factor classification based on 100 subsets of trn; and the third picture presents the ROC and AUC, which have been counted 100 times based on 100 subsets of trn. The fourth figure is a statistical chart of fitting performance and prediction performance of the single-factor WoE model based on 100 subsets of trn, where the blue line is the mean ROC (ROC_trn2trn) of the model's fitting performance to 100 subsets of trn, the gray band is the ROC range of the model's fitting performance to 100 subsets of trn, and the orange line is the ROC(ROC_trn2TST) of the model's prediction performance statistics to TST.
4.3. Test Results for Conditional Independence
The independence of 14 factors with AUCs>0.59 was analyzed (Figure 21). Figure 21 combines the statistical results of two correlation indexes, Pearson’s C and Cramer's V, which are located in the upper right half and the lower left half of the heat map, respectively. The results show that according to Pearson’s C index, Rou and TRI (0.81) and Rou and SL (0.71) are strongly correlated factor pairs. However, according to Cramer's V, the correlation among the factors involved in statistics is not strong (≤0.60). DF, HANDH and dCN have a low correlation with all other factors. Elevation and its derived TRI, Rou, RSP and SL are slightly related.
4.4. Step-by-step Modeling Results of Landslide Susceptibility
(1) Comprehensively considering the independence indexes of the factors, such as Pearson’s C and Cramer's V, and AUCs (AUC_trn, AUC_trn2trn and AUC_trn2TST), six factors with AUC_trn ≥0.63, AUC_trn2trn ≥0.63 and AUC_trn2tst ≥0.64 were selected for modeling, including dRD, HANDV, NDVIlog, SL, RSP and TRI.
(2) On the basis of M6, Rou and HANDH with AUC_trn≥ 0.64, AUC_trn2trn≥ 0.62 and AUC_trn2TST≥ 0.61 were added in turn. A seven-factor model (M7) and an eight-factor model (M8) was constructed, respectively, which improved AUC_M and were selected as the basic models for the next modeling step.
(3) On the basis of M8, we tried to increase dF, Lth and dCN with indexes ≥ 0.63, ≥ 0.62 and ≥ 0.60 and construct M9, M9 (1) and M9 (2). M9, M9 (1) and M9 (2) have different degrees of improvement compared with M8, especially M9. We took M9 as the basis of the next modeling step.
(4) On the basis of M9, M10 (M9+Lth) and M10(1) (M9+dCN) were compared, and the AUC of M10 model was higher than that of M9, so it was selected as the basis for the next modeling step.
(5) On the basis of M10, M11 (M10+dCN) was tested. Although the AUC of the model did not increase, the coincidence between ROC_M_trn2trn and ROC_M_trn2TST was significantly improved.
(6) On the basis of M11, M12 (M11 + CProf), M13 (M11 + CProf + CLCD) and M14 (M11 + CProf + CLCD + DEM) were tested. Compared with M11, M12 not only did not improve AUC_M, but also the coincidence between ROC_M_trn2trn and ROC_M_trn2TST became worse. Compared with M11, although ROC_M_trn2trn and ROC_M_trn2TST were in good agreement, AUC_M was not improved. Therefore, the effect of adding CProf, CLCD and DEM to M11 was not obvious.
(7) To sum up, the model M11 is the best model.
As shown in Figure 22, the success rate of the model M11 is represented by the ROC calculated by using trn, and its AUC index is ~0.87. The AUC index of the prediction rate calculated using TST was ~0.87 too. Both of them are high, being within the range of excellent classification models. The results show that 11 factors are enough to create the most effective map of landslide susceptibility in the study area.
Table 2.
Comparison of validity and accuracy (AUCs) of models.

4.5. Landslide Susceptibility Mapping Results
Based on the ROC_M_trn2trn of model M11, we compiled the landslide susceptibility zoning map (Figure 23). Very-high-susceptibility areas (VHS), which comprise only 5.05% of the study area, contain 50% of landslides, and high-susceptibility areas (HS), which comprise 14.53% of the study area, contain 30% of landslides (Figure 23, Table 3). Therefore, the high-susceptibility (HS) and the very-high-susceptibility areas (VHS), with an area accounting for 19.58% of the study areas, containing 80% of the landslides. These characteristics of the landslide susceptibility zoning map represent the potential for the first-order prediction of landslides in this landscape.
5. Discussion
5.1. Landslide Susceptibility Zoning and Disaster Prevention Deployment Strategy
Based on the above work, we compiled the landslide susceptibility map of the Dianchi Lake watershed, which has great practical significance. The map provides basic information relating to landslide disasters for spatial planners. It can be used to determine the regional priority for further investigation, support the local planning activities of regional geological disaster prevention and ecological restoration, or create a regional landslide risk exposure assessment. The latter can evaluate the existing elements with landslide risk or those still under planning.
The landslide susceptibility map developed in this paper can effectively predict known and unknown landslides. The fitting accuracy and prediction accuracy of the best model M11 are both ~0.87, and the model coincidence is excellent (Figure 22, Table 2). Moreover, ROC_M_trn2TST is in good coincidence with the range of ROC_M_trn2trn (Figure 22, Table 2), indicating that there is no over-fitting or under-fitting. When 19.58% of the research area is defined as high susceptibility (VHS+HS), the model predicts 80% of the landslides (Figure 23, Table 3). The above results obtained from the analysis are satisfactory for the Dianchi Lake watershed.
The landslide susceptibility map developed in this paper reveals that the area with high susceptibility (VHS+HS) is large, accounting for ~20% of study area (excluding the area with flat and water surface), which shows that the natural landslide susceptibility intensity in the Dianchi Lake Watershed is large, which poses a great challenge for the comprehensive prevention and control of geological disasters, and this work has a long way to go. In particular, there are large areas of high susceptibility (VHS+HS) in the mountainous area of the northern basin edge of Kunming urban area, and it is almost contiguous. These areas are close to Kunming city and Dianchi Lake waters, which have great influence on urban safety and Dianchi Lake water protection, and should be taken as the key areas for landslide prevention and control. Another area with high susceptibility (VHS+HS) is the southeast of the study area, which should also be subjected to mitigation and preventative activities.
5.2. Important Factors of Landslide Susceptibility and High Sensitivity and Disaster Prevention Strategies
AUCs (AUC_ALL, AUC_trn, AUC_trn2trn, AUC_trn2TST) of single factors quantify the sensitivity (spatial correlation) of the landslide impact of each factor, and the weight of evidence of single factors (WoE_ALL, WoE_trn) reveals the impact of each classification on the spatial distribution of landslide,while sC defines the significance of the difference between classifications. AUCs, WoEs and sCs are meaningful indicators to quantify the sensitivity of landslide impact.
We have identified more reliable landslide control factors. The analysis results of this paper (Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19 and Figure 20) show 13 factors with AUC ≥ 0.6 from high to low AUC: dRD, HANDV, NDVIlog, SL, RSP, TRI, Rou, Lth, dF, HANDH, Cprof, dCN, and CLCD (Table 4). The optimal landslide susceptibility model represents a combination of 11 factors: dRD, HANDV, NDVIlog, SL, RSP, TRI, Rou, Lth, dF, HANDH, and dCN. In the process of step-by-step modeling, Cprof, dCN and CLCD were all rejected because they did not contribute to the explanatory power of the model, as evaluated using ROC_M.
We pay attention to which classification of the above important factors is more conducive to the occurrence of landslides. We analyzed the factor classification of (Table 5).
The above results suggest that we should pay attention to the natural conditions and human factors represented by dRD, HANDV, NDVIlog, SL, RSP, TRI, Rou, Lth, dF, HANDH, dCN, CProf and CLCD, coordinate prevention with planning, construction and protection, and reduce the induction of landslides. Attention should be paid to the slope stability support within 100m on both sides of the road, and development should be reduced in steep slope areas (25-40°), in areas where the height difference between the two sides of the stream is 13-67m and in low vegetation coverage areas. Attention should be paid to the conservation and protection of forest vegetation, and the distribution map should be used to avoid weak rocks such as the affected areas of fault zones and shale siltstone.
5.3. The Landslide Susceptibility Evaluation Based on the WoE Method May be Improved
The optimized classification process sets the classification value based on the nearly continuous cumulative sC curve of evidence weight distribution and then carries out WoE statistics, which captures the trend of evidence weight distribution, overcomes the discontinuity of evidence weight distribution in traditional methods, improves the discrimination of landslide sensitivity of each influencing factor and reduces the subjectivity of factor classification.
The uncertainty analysis obtained by using sub-sampling cross-validation technology allows us to verify the weighted uncertainty sampling process related to the introduced error [6]. The trn and TST are spatial random sub-samples of the same size from the same dataset, ALL, which represent the same spatial distribution but have different mean sampling error (MSE) related to sample size [4]. The model performance evaluation based on TST, which is smaller than TRN, must take this into account in order to correctly interpret the model analysis results [16]. MSE based on trn defines the uncertainty of model performance. If the model is well summarized and there is no obvious over-fitting, the ROC curve and AUC value should fall within the MSE range when evaluating the model with corresponding TST [4]. Therefore, compared with no sampling (analysis with all landslide data), this analysis is advantageous because the potential impact of random sub-sampling is considered.
We compared the accuracy and predictive performance of 14 models with different factor combinations. The optimal model M11 determined in this paper contains Rou, TRI and SL with Pearson’s C index > 0.7, but the ROC_M_trn2TST of the model not only does not show over-fitting, but also shows excellent coincidence. We think that it is not appropriate to exclude the modeling factors only according to Pearson’s C index, and it may be more feasible to comprehensively determine the Cramer's V index and ROC_M.
The improved comprehensive process proposed in this paper combines many techniques, such as optimized classification, cross-validation and step-by-step modeling, and obtains the model with high accuracy and predictive performance, which shows that this process has good practical value and may improve the landslide susceptibility evaluation based on the WoE method, which is worthy of further promotion and application in similar areas.
5.4. Restrictions
According to the research of [46], the abundance of landslide list is a critical resource that affects susceptibility modeling, and is more important than the detailed data of influencing factors. The landslide data used in this paper may be incomplete, which may have some influence on the analysis results of this paper. In the future, it is necessary to strengthen the compilation of a more complete landslide inventory based on remote sensing.
Regarding the improved technical process and factor classification optimization process of the landslide susceptibility evaluation model based on WoE method put forward in this paper, although more effective modeling results have been obtained in the research area, it still requires more demonstration areas for testing. Furthermore, the process proposed in this paper is not highly automated and needs more manual intervention. In the future, research should be deepened to form a more convenient data-driven process.
6. Conclusion
Dianchi Lake is the largest of the nine plateau lakes in Yunnan Plateau. These nine plateau lake watersheds are important ecological protection areas in southwest China. It is of great practical significance to evaluate and analyze the landslide susceptibility in the Dianchi Lake watershed for disaster prevention and mitigation, ecological protection and restoration planning. In this paper, firstly, a factor optimization classification process was developed on the basis of the traditional WoE method, and the landslide susceptibility evaluation process based on the WoE method was perfected. Based on the spatial distribution data of historical landslides, a factor classification scheme was put forward, the landslide susceptibility sensitivity of each factor was evaluated, the important landslide susceptibility control factors were screened out, the landslide susceptibility evaluation model was established, and the landslide susceptibility distribution in the study area was evaluated and analyzed. The main conclusions are as follows:
(1) An improved technical process of landslide susceptibility assessment model based on the WoE method was put forward and successfully applied, a factor classification optimization process was developed, and a highly effective model (AUC=0.87) was established, which made a new contribution to the improvement of landslide susceptibility assessment technology based on the WoE method.
(2) According to the results, eleven factors, such as dRD, HANDV, NDVIlog, SL, RSP, TRI, Rou, Lth, dF, HANDH, and dCN, were identified as the key sensitive factors of landslide in the study area, which should be considered in landslide prevention, monitoring and early warning facility layout and ecological restoration planning.
(3) The landslide susceptibility map developed in this paper reveals that the area of high susceptibility (VHS+HS) in the Dianchi Lake watershed is large, and the comprehensive prevention and control of landslides have a long way to go. The large-scale and contiguous high-susceptibility areas in the mountainous areas on the edge of the basin present the urban safety of Kunming and the water protection of Dianchi Lake with serious landslide hazards, and so the investigation, monitoring and risk assessment of landslide hazards should be strengthened.
Author Contributions
Conceptualization, G.B., X.Y. and Z.K.; methodology, G.B. and X.Y.; software, G.B. and X.Y.; validation, G.B., X.Y. and Z.K.; formal analysis, G.B. and X.Y.; investigation, G.B., X.Y., Z.K., J. Z., S. Z., and B.S.; resources, G.B. X.Y. and Z.K.; data curation, Z.K. and S.Z.; writing—original draft preparation, G.B., X.Y. and Z.K.; writing—review and editing, G.B., X.Y., Z.K., J.Z., B.S. and S.Z.; visualization, G.B. and X.Y.; supervision, Z.K. and S.Z.; project administration, S.Z. and J.Z.; funding acquisition, S.Z. and J.Z.. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the science and technology development project of Power China, Sinohydro Foundation Engineering Co., Ltd. (Tianjin, China), the evaluation of rapid excavation of slope cut-off wall in complex geological background area and treatment technology of mud and water inrush in tunnel engineering (Grant No. 2022530103001936), and the scientific and technological development project of Southwest Pipeline Co., Ltd. (Chengdu, China), National Pipe Network Group Research on Hydraulic Protection and Soil and Water Conservation of Oil and Gas Pipelines through Fully Weathered Granite Area (Grant No. 2018016).
Data Availability Statement
The datasets for this study can be obtained by contacting the first author or corresponding author.
Acknowledgments
We are very grateful to the colleagues in the team who supported the implementation of this project. We are sincerely thankful to Torizin J. for providing data processing software LSAT PM. We are also sincerely thankful to the editors and reviewers.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Regmi, N.R.; Giardino, J.R.; Vitek, J.D. Modeling susceptibility to landslides using the weight of evidence approach: Western Colorado, USA. Geomorphology 2010, 115, 172–187. [Google Scholar] [CrossRef]
- Bai, G.; Yang, X.; Zhu, J.; Zhang, S.; Zhu, C.; Kang, X.; Sun, B.; Zhou, Y. Susceptibility assessment of geological hazards in Wuhua District of Kuming, China using the weight evidence method. The Chinese Journal of Geological Hazard and Control 2022, 33, 128–138. [Google Scholar]
- Guzzetti, F.; Reichenbach, P.; Cardinali, M.; Galli, M.; Ardizzone, F. Probabilistic landslide hazard assessment at the basin scale. Geomorphology 2005, 72, 272–299. [Google Scholar] [CrossRef]
- Torizin, J.; Schüßler, N.; Fuchs, M. Landslide Susceptibility Assessment Tools v1.0.0b – Project Manager Suite: a new modular toolkit for landslide susceptibility assessment. Geosci Model Dev 2022, 15, 2791–2812. [Google Scholar] [CrossRef]
- Guzzetti, F.; Cardinali, M.; Reichenbach, P.; Carrara, A. Comparing Landslide Maps: A Case Study in the Upper Tiber River Basin, Central Italy. Environ Manage 2000, 25, 247–263. [Google Scholar] [CrossRef]
- Torizin, J.; Fuchs, M.; Awan, A.A.; Ahmad, I.; Akhtar, S.S.; Sadiq, S.; Razzak, A.; Weggenmann, D.; Fawad, F.; Khalid, N.; et al. Statistical landslide susceptibility assessment of the Mansehra and Torghar districts, Khyber Pakhtunkhwa Province, Pakistan. Nat Hazards 2017, 89, 757–784. [Google Scholar] [CrossRef]
- Torizin, J.; Wang, L.; Fuchs, M.; Tong, B.; Balzer, D.; Wan, L.; Kuhn, D.; Li, A.; Chen, L. Statistical landslide susceptibility assessment in a dynamic environment: A case study for Lanzhou City, Gansu Province, NW China. J Mt Sci-Engl 2018, 15, 1299–1318. [Google Scholar] [CrossRef]
- Bonham-Carter, G.; Agterberg, F.P.; Wright, D.F. Weight of evidence modeling: A new approach to mapping mineral potential. Geology Survey of Canada 1989, 89, 171–183. [Google Scholar]
- Torizin, J. Elimination of informational redundancy in the weight of evidence method: an application to landslide susceptibility assessment. Stoch Env Res Risk A 2016, 30, 635–651. [Google Scholar] [CrossRef]
- Alsabhan, A.H.; Singh, K.; Sharma, A.; Alam, S.; Pandey, D.D.; Rahman, S.A.S.; Khursheed, A.; Munshi, F.M. Landslide susceptibility assessment in the Himalayan range based along Kasauli – Parwanoo road corridor using weight of evidence, information value, and frequency ratio. Journal of King Saud University - Science 2022, 34, 101759. [Google Scholar] [CrossRef]
- Chen, L.; Guo, H.; Gong, P.; Yang, Y.; Zuo, Z.; Gu, M. Landslide susceptibility assessment using weights-of-evidence model and cluster analysis along the highways in the Hubei section of the Three Gorges Reservoir Area. Comput Geosci-Uk 2021, 156, 104899. [Google Scholar] [CrossRef]
- Mathew, J.; Jha, V.K.; Rawat, G.S. Weights of evidence modelling for landslide hazard zonation mapping in part of Bhagirathi valley, Uttarakhand. Current Science (Bangalore) 2007, 92, 628–638. [Google Scholar]
- Neuhäuser, B.; Terhorst, B. Landslide susceptibility assessment using “weights-of-evidence” applied to a study area at the Jurassic escarpment (SW-Germany). Geomorphology 2007, 86, 12–24. [Google Scholar] [CrossRef]
- Saha, A.; Saha, S. Comparing the efficiency of weight of evidence, support vector machine and their ensemble approaches in landslide susceptibility modelling: A study on Kurseong region of Darjeeling Himalaya, India. Remote Sensing Applications: Society and Environment 2020, 19, 100323. [Google Scholar] [CrossRef]
- Teerarungsigul, S.; Torizin, J.; Fuchs, M.; Kühn, F.; Chonglakmani, C. An integrative approach for regional landslide susceptibility assessment using weight of evidence method: a case study of Yom River Basin, Phrae Province, Northern Thailand. Landslides 2016, 13, 1151–1165. [Google Scholar] [CrossRef]
- Torizin, J.; Fuchs, M.; Kuhn, D.; Balzer, D.; Wang, L. Practical Accounting for Uncertainties in Data-Driven Landslide Susceptibility Models. Examples from the Lanzhou Case Study. In Understanding and Reducing Landslide Disaster Risk: Volume 2 From Mapping to Hazard and Risk Zonation, Guzzetti, F., Mihalić Arbanas, S., Reichenbach, P., Sassa, K., Bobrowsky, P.T., Takara, K., Eds.; Springer International Publishing: Cham, 2021; pp. 249–255. [Google Scholar]
- Jasiewicz, J.; Stepinski, T.F. Geomorphons — a pattern recognition approach to classification and mapping of landforms. Geomorphology 2013, 182, 147–156. [Google Scholar] [CrossRef]
- Stepinski, T.F.; Jasiewicz, J. Geomorphons - a new approach to classification of landforms. Proceedings of Geomorphometry 2011, Hengl, T.; Evans, I.S.; Wilson, J.P.; Gould, M.,Eds. Redlands; 2011; pp. 109–112. [Google Scholar]
- Yang, J.; Huang, X. The 30m annual land cover dataset and its dynamics in China from 1990 to 2019. Earth Syst Sci Data 2021, 13, 3907–3925. [Google Scholar] [CrossRef]
- Chung, C.; Fabbri, A.G. Predicting landslides for risk analysis — Spatial models tested by a cross-validation technique. Geomorphology 2008, 94, 438–452. [Google Scholar] [CrossRef]
- Xu, Y.; Goodacre, R. On Splitting Training and Validation Set: A Comparative Study of Cross-Validation, Bootstrap and Systematic Sampling for Estimating the Generalization Performance of Supervised Learning. J Anal Test 2018, 2, 249–262. [Google Scholar] [CrossRef]
- He, Q.; Wang, M.; Liu, K. Rapidly assessing earthquake-induced landslide susceptibility on a global scale using random forest. Geomorphology 2021, 391, 107889. [Google Scholar] [CrossRef]
- Lan, H.; Tian, N.; Li, L.; Wu, Y.; Macciotta, R.; Clague, J.J. Kinematic-based landslide risk management for the Sichuan-Tibet Grid Interconnection Project (STGIP) in China. Eng Geol 2022, 308, 106823. [Google Scholar] [CrossRef]
- Tanyaş, H.; Görüm, T.; Fadel, I.; Yıldırım, C.; Lombardo, L. An open dataset for landslides triggered by the 2016 Mw 7.8 Kaikōura earthquake, New Zealand. Landslides 2022, 19, 1405–1420. [Google Scholar] [CrossRef]
- Xiong, H.; Ma, C.; Li, M.; Tan, J.; Wang, Y. Landslide susceptibility prediction considering land use change and human activity: A case study under rapid urban expansion and afforestation in China. Sci Total Environ 2023, 866, 161430. [Google Scholar] [CrossRef]
- Zhang, Y.; Ayyub, B.M.; Gong, W.; Tang, H. Risk assessment of roadway networks exposed to landslides in mountainous regions—a case study in Fengjie County, China. Landslides 2023. [Google Scholar] [CrossRef]
- Guzzetti, F.; Mondini, A.C.; Cardinali, M.; Fiorucci, F.; Santangelo, M.; Chang, K. Landslide inventory maps: New tools for an old problem. Earth-Sci Rev 2012, 112, 42–66. [Google Scholar] [CrossRef]
- Zanaga, D.; Van De Kerchove, R.; De Keersmaecker, W.; Souverijns, N.; Brockmann, C.; Quast, R.; Wevers, J.; Grosu, A.; Paccini, A.; Vergnaud, S.; et al. ESA WorldCover 10 m 2020 v100 [Data set]. In 2021.
- Xu, X. China 30m Annual NDVI Maximum Dataset [Data set]. Resource and Environmental Science Data Registration and Publishing System 2022. [Google Scholar]
- JPL, N. NASADEM Merged DEM Global 1 arc second V001. Accessed 2020-12-30 from doi:10.5067/MEaSUREs/NASADEM/NASADEM_HGT.001 [Data set]. Nasa Eosdis Land Processes Daac. 2020. [CrossRef]
- Guisan, A.; Weiss, S.B.; Weiss, A.D. GLM versus CCA spatial modeling of plant species distribution. Plant Ecol 1999, 143, 107–122. [Google Scholar] [CrossRef]
- Riley, S.; Degloria, S.; Elliot, S.D. A Terrain Ruggedness Index that Quantifies Topographic Heterogeneity. Internation Journal of Science 1999, 5, 23–27. [Google Scholar]
- Nobre, A.D.; Cuartas, L.A.; Hodnett, M.; Rennó, C.D.; Rodrigues, G.; Silveira, A.; Waterloo, M.; Saleska, S. Height Above the Nearest Drainage – a hydrologically relevant new terrain model. J Hydrol 2011, 404, 13–29. [Google Scholar] [CrossRef]
- Rennó, C.D.; Nobre, A.D.; Cuartas, L.A.; Soares, J.V.; Hodnett, M.G.; Tomasella, J.; Waterloo, M.J. HAND, a new terrain descriptor using SRTM-DEM: Mapping terra-firme rainforest environments in Amazonia. Remote Sens Environ 2008, 112, 3469–3481. [Google Scholar] [CrossRef]
- Moore, I.D.; Grayson, R.B.; Ladson, A.R. Digital terrain modelling: A review of hydrological, geomorphological, and biological applications. Hydrol Process 1991, 5, 3–30. [Google Scholar] [CrossRef]
- Beven, K.; Kirkby, M. A Physically Based, Variable Contributing Area Model of Basin Hydrology. Hydrol. Sci. Bull. 1979, 24, 43–69. [Google Scholar] [CrossRef]
- Böhner, J.; Selige, T. Spatial prediction of soil attributes using terrain analysis and climate regionalisation. Saga - Analysis and Modelling Applications 2006, 115, 13–27. [Google Scholar]
- Böhner, J.; Koethe, R.; Conrad, O.; Gross, J.; Ringeler, A.; Selige, T. Soil regionalisation by means of terrain analysis and process parameterisation. Soil Classification 2001 2002, 213–222. [Google Scholar]
- Agterberg, F.P.; Bonham-Carter, G.F.; Cheng, Q.; Wright, D.F.; Davis, J.C.; Herzfeld, U.C. Weights of evidence modeling and weighted logistic regression for mineral potential mapping. Computers in Geology--25 Years of Progress 1993, 5, 13–32. [Google Scholar]
- Agterberg, F.P. Combining indicator patterns in weights of evidence modeling for resource evaluation. Nonrenewable Resources 1992, 1, 39–50. [Google Scholar] [CrossRef]
- Agterberg, F.P.; Bonham-Carter, G.F.; Wright, D.F. Statistical Pattern Integration for Mineral Exploration**Geological Survey of Canada Contribution No. 24088. In Computer Applications in Resource Estimation, GAÁL, G.; MERRIAM, D.F., Ed.; Pergamon: Amsterdam, 1990; pp. 1–21. [Google Scholar]
- Bonham-Carter, G.F. Geographic Information Systems for Geoscientists: Modelling with GIS. Pergamon: Canada, 1994; p 1-398.
- Fawcett, T. An introduction to ROC analysis. Pattern Recogn Lett 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Agterberg, F.P.; Cheng, Q. Conditional Independence Test for Weights-of-Evidence Modeling. Nat Resour Res 2002, 11, 249–255. [Google Scholar] [CrossRef]
- Chung, C.F.; Fabbri, A.G. Validation of Spatial Prediction Models for Landslide Hazard Mapping. Nat Hazards 2003, 30, 451–472. [Google Scholar] [CrossRef]
- Depicker, A.; Jacobs, L.; Delvaux, D.; Havenith, H.; Maki Mateso, J.; Govers, G.; Dewitte, O. The added value of a regional landslide susceptibility assessment: The western branch of the East African Rift. Geomorphology 2020, 353, 106886. [Google Scholar] [CrossRef]
Figure 1.
Study area. (a) The location of Yunnan province in China. (b) The distribution of nine plateau lake watersheds in Yunnan, and the location of the Dianchi Lake watershed. The base map is the distribution map of land coverage types in Yunnan Province in 2020 [19]; (c) The distribution map of landslide points in Dianchi Lake watershed, the black points are landslides under investigation, the blue blocks are the water surface, and the gray diagonal lines are the areas with the attribute of "flat" [17,18], and the bottom picture is rendered by elevation and hill shade.
Figure 1.
Study area. (a) The location of Yunnan province in China. (b) The distribution of nine plateau lake watersheds in Yunnan, and the location of the Dianchi Lake watershed. The base map is the distribution map of land coverage types in Yunnan Province in 2020 [19]; (c) The distribution map of landslide points in Dianchi Lake watershed, the black points are landslides under investigation, the blue blocks are the water surface, and the gray diagonal lines are the areas with the attribute of "flat" [17,18], and the bottom picture is rendered by elevation and hill shade.

Figure 2.
Process flow chart of cross-validation landslide dataset compilation based on random sampling.
Figure 2.
Process flow chart of cross-validation landslide dataset compilation based on random sampling.

Figure 6.
Process flow chart of factor classification optimization strategy based on the cumulative sC curve and WoE statistics.
Figure 6.
Process flow chart of factor classification optimization strategy based on the cumulative sC curve and WoE statistics.

Figure 7.
The frequency distribution of some factors' original data and the cumulative sC statistical curve of multiple quantiles. There are two statistical result graphs for each factor—the upper graph is the frequency distribution graph of the original factor data, and the lower graph is the cumulative sC curve of statistics after the original factor data are dispersed according to six quantiles of 100, 80, 60, 40, 20 and 10.
Figure 7.
The frequency distribution of some factors' original data and the cumulative sC statistical curve of multiple quantiles. There are two statistical result graphs for each factor—the upper graph is the frequency distribution graph of the original factor data, and the lower graph is the cumulative sC curve of statistics after the original factor data are dispersed according to six quantiles of 100, 80, 60, 40, 20 and 10.

Figure 8.
Graphical result output of WoE analysis for the factor dF. Class 1 is 0-121m; class 3 is 262-460m; class 5 is 657-864m; class 7 is 1355-2317m; and class 99 is other ranges.
Figure 8.
Graphical result output of WoE analysis for the factor dF. Class 1 is 0-121m; class 3 is 262-460m; class 5 is 657-864m; class 7 is 1355-2317m; and class 99 is other ranges.

Figure 9.
Graphical result output of WoE analysis for the factor Lth. Class 10 is loose gravel soil, class 23 is sandstone, mudstone and shale, class 24 is mudstone, shale and siltstone, class 51 is basalt and class 199 is other lithologic strata, including limestone and metamorphic rocks.
Figure 9.
Graphical result output of WoE analysis for the factor Lth. Class 10 is loose gravel soil, class 23 is sandstone, mudstone and shale, class 24 is mudstone, shale and siltstone, class 51 is basalt and class 199 is other lithologic strata, including limestone and metamorphic rocks.

Figure 10.
Graphical result output of WoE analysis for the factor NDVIlog. Class 1 is 2.79-3.64, class 2 is 3.64-3.71, class 3 is 3.71-3.76, class 4 is 3.76-3.81, class 5 is 3.81-3.84, class 6 is 3.84-3.85, class 7 is 3.85-3.88, and class 8 is 3.88-3.99.
Figure 10.
Graphical result output of WoE analysis for the factor NDVIlog. Class 1 is 2.79-3.64, class 2 is 3.64-3.71, class 3 is 3.71-3.76, class 4 is 3.76-3.81, class 5 is 3.81-3.84, class 6 is 3.84-3.85, class 7 is 3.85-3.88, and class 8 is 3.88-3.99.

Figure 11.
Graphical result output of WoE analysis for the factor dRD. Class 1 is 0-22.81m, class 2 is 22.81-44.56m, class 3 is 44.56-71.39m, class 4 is 71.39-99.68m, class 5 is 99.68-157.42m, class 6 is 157.42-306.85m, class 7 is 306.85-458.95m, class 8 is 458.95-602.39m, and class 9 is 602.39-2936.07m.
Figure 11.
Graphical result output of WoE analysis for the factor dRD. Class 1 is 0-22.81m, class 2 is 22.81-44.56m, class 3 is 44.56-71.39m, class 4 is 71.39-99.68m, class 5 is 99.68-157.42m, class 6 is 157.42-306.85m, class 7 is 306.85-458.95m, class 8 is 458.95-602.39m, and class 9 is 602.39-2936.07m.

Figure 12.
Graphical result output of WoE analysis for the factor TRI. Class 1 is 0.00-11.58m, class 2 is 11.58-20.62m, class 3 is 20.62-22.98m, class 5 is 41.98-45.47m, class 7 is 48.89-52.50m, class 8 is 52.50-58.39m, class 10 is 112.52-125.38m, and class 99 is others in the range of 0-447.60m.
Figure 12.
Graphical result output of WoE analysis for the factor TRI. Class 1 is 0.00-11.58m, class 2 is 11.58-20.62m, class 3 is 20.62-22.98m, class 5 is 41.98-45.47m, class 7 is 48.89-52.50m, class 8 is 52.50-58.39m, class 10 is 112.52-125.38m, and class 99 is others in the range of 0-447.60m.

Figure 13.
Graphical result output of WoE analysis for the factor Rou. Class 1 is 0.00-8.93, class 2 is 8.93-16.53, class 3 is 16.53-24.95, class 4 is 24.95-28.88, class 5 is 28.88-40.73, class 6 is 40.73-44.33, class 7 is 44.33-49.50, class 8 is 49.50-52.52, class 9 is 52.52-57.22, class 10 is 57.22-62.32, and class 11 is 62.32-398.73.
Figure 13.
Graphical result output of WoE analysis for the factor Rou. Class 1 is 0.00-8.93, class 2 is 8.93-16.53, class 3 is 16.53-24.95, class 4 is 24.95-28.88, class 5 is 28.88-40.73, class 6 is 40.73-44.33, class 7 is 44.33-49.50, class 8 is 49.50-52.52, class 9 is 52.52-57.22, class 10 is 57.22-62.32, and class 11 is 62.32-398.73.

Figure 14.
Graphical result output of WoE analysis for the factor RSP. Class 1 is 0-0.01, class 2 is 0.01-0.02, class 3 is 0.02-0.05, class 4 is 0.05-0.06, class 5 is 0.06-0.08, class 6 is 0.08-0.14, class 7 is 0.14-0.29, class 8 is 0.29-0.45, and class 9 is 0.45-1.02.
Figure 14.
Graphical result output of WoE analysis for the factor RSP. Class 1 is 0-0.01, class 2 is 0.01-0.02, class 3 is 0.02-0.05, class 4 is 0.05-0.06, class 5 is 0.06-0.08, class 6 is 0.08-0.14, class 7 is 0.14-0.29, class 8 is 0.29-0.45, and class 9 is 0.45-1.02.

Figure 15.
Graphical result output of WoE analysis for the factor SL. Class1 is 0-4.12°, class3 is 6.44-7.65°, class5 is 10.83-11.65°, class6 is 11.65-16.13°, class8 is 17.12-21.10°, class10 is 25.60-28.27°, class11 is 28.27-39.98°, and class99 is other slopes.
Figure 15.
Graphical result output of WoE analysis for the factor SL. Class1 is 0-4.12°, class3 is 6.44-7.65°, class5 is 10.83-11.65°, class6 is 11.65-16.13°, class8 is 17.12-21.10°, class10 is 25.60-28.27°, class11 is 28.27-39.98°, and class99 is other slopes.

Figure 16.
Graphical result output of WoE analysis for the factor HANDH. Class 1~class 13 are divided by 0m, 38.06m, 49.60m, 65.22m, 100.45m, 115.44m, 184.98m, 1255.91m, 271.86m, 302.28m, 323.25m, 439.08m, 1176.82m, and 2831.14m.
Figure 16.
Graphical result output of WoE analysis for the factor HANDH. Class 1~class 13 are divided by 0m, 38.06m, 49.60m, 65.22m, 100.45m, 115.44m, 184.98m, 1255.91m, 271.86m, 302.28m, 323.25m, 439.08m, 1176.82m, and 2831.14m.

Figure 17.
Graphical result output of WoE analysis for the factor dCN. Class 1~class 14 are divided by 0m, 22.33m, 24.98m, 40.21m, 49.85m, 67.45m, 94.96m, 113.16m, 134.62m, 174.57m, 240.09m, 279.41m, 320.53m, 394.72m, and more than 394.72m.
Figure 17.
Graphical result output of WoE analysis for the factor dCN. Class 1~class 14 are divided by 0m, 22.33m, 24.98m, 40.21m, 49.85m, 67.45m, 94.96m, 113.16m, 134.62m, 174.57m, 240.09m, 279.41m, 320.53m, 394.72m, and more than 394.72m.

Figure 18.
Graphical result output of WoE analysis for the factor HANDV. Class 1~class 15 are divided by 0m, 4.15m, 6.93m, 13.03m, 15.61m, 17.89m, 24.11m, 26.22m, 34.53m, 37.77m, 41.57m, 55.48m, 66.60m, 77.37m, 101.59m, and 570.01m.
Figure 18.
Graphical result output of WoE analysis for the factor HANDV. Class 1~class 15 are divided by 0m, 4.15m, 6.93m, 13.03m, 15.61m, 17.89m, 24.11m, 26.22m, 34.53m, 37.77m, 41.57m, 55.48m, 66.60m, 77.37m, 101.59m, and 570.01m.

Figure 19.
Graphical result output of WoE analysis for the factor CLCD. Class 2 is forest, class 4 is grassland, and class 99 is others (cropland, shrub, barren, impervious, wetland).
Figure 19.
Graphical result output of WoE analysis for the factor CLCD. Class 2 is forest, class 4 is grassland, and class 99 is others (cropland, shrub, barren, impervious, wetland).

Figure 20.
Graphical result output of WoE analysis for the factor Cprof. Class 1 is -12611.46~-4084.50 (×10-6), class 2 is -4084.50~-2981.60 (×10-6), class 3 is -2981.60~-1533.30 (×10-6), class 4 is -1533.30~-973.62 (×10-6), class 5 is -973.62~-686.55 (×10-6), class 6 is -686.55~37.07 (×10-6), and class 7 is 37.07~10596.92(×10-6).
Figure 20.
Graphical result output of WoE analysis for the factor Cprof. Class 1 is -12611.46~-4084.50 (×10-6), class 2 is -4084.50~-2981.60 (×10-6), class 3 is -2981.60~-1533.30 (×10-6), class 4 is -1533.30~-973.62 (×10-6), class 5 is -973.62~-686.55 (×10-6), class 6 is -686.55~37.07 (×10-6), and class 7 is 37.07~10596.92(×10-6).

Figure 21.
Test results for conditional dependence. The upper right half represents the Pearson’s C results, and the factors with a strong correlation indicated by > 0.7 are determined by black circles, such as Rou and TRI (0.81), Rou and SL (0.71), and dCN and HANDH (0.82). The lower left presents the Cramer's V results.
Figure 21.
Test results for conditional dependence. The upper right half represents the Pearson’s C results, and the factors with a strong correlation indicated by > 0.7 are determined by black circles, such as Rou and TRI (0.81), Rou and SL (0.71), and dCN and HANDH (0.82). The lower left presents the Cramer's V results.

Figure 22.
Accuracy and validity assessment of the models. Accuracy assessment of the models of susceptibility to landslides with the ROC_trn2trn of models (The blue line and the grey range. The total weights for the models were based on trn and the performance of the models was evaluated using trn. One hundred iterations were carried out. The blue line is the mean ROC_M of 100 iterations. The grey range marks the model uncertainty based on the ROCs' MSE of 100 iterations.) Test of validity of the models with the ROC_M_trn2TST (the orange line). The total weight maps were based on the trn and the validation was assessed by using the TST.
Figure 22.
Accuracy and validity assessment of the models. Accuracy assessment of the models of susceptibility to landslides with the ROC_trn2trn of models (The blue line and the grey range. The total weights for the models were based on trn and the performance of the models was evaluated using trn. One hundred iterations were carried out. The blue line is the mean ROC_M of 100 iterations. The grey range marks the model uncertainty based on the ROCs' MSE of 100 iterations.) Test of validity of the models with the ROC_M_trn2TST (the orange line). The total weight maps were based on the trn and the validation was assessed by using the TST.

Figure 23.
Susceptibility map to landslides based on model M11 and trn. The model M11 has the highest rate of accuracy and validity. (a) and (b) are compiled using the same susceptibility partition data. The differences are as follows: (b) MS, LS and VLS use the same general gray color to highlight VHS and HS. VHS areas account for 5.05% of the study area and contain 50% of the total number of landslides. HS areas account for 14.53% of the study area and contain 30% of the total number of landslides. MS areas account for 28.23% of the study area and contain 15% of the total number of landslides. LS areas account for 32.55% of the study area and contain 4% of the total number of landslides. VLS areas account for 19.64% of the study area and contains 1% of the total number of landslides. The bottom picture is rendered using elevation and hill shade. The red ellipse roughly delineates the areas with high susceptibility and contiguous distribution.
Figure 23.
Susceptibility map to landslides based on model M11 and trn. The model M11 has the highest rate of accuracy and validity. (a) and (b) are compiled using the same susceptibility partition data. The differences are as follows: (b) MS, LS and VLS use the same general gray color to highlight VHS and HS. VHS areas account for 5.05% of the study area and contain 50% of the total number of landslides. HS areas account for 14.53% of the study area and contain 30% of the total number of landslides. MS areas account for 28.23% of the study area and contain 15% of the total number of landslides. LS areas account for 32.55% of the study area and contain 4% of the total number of landslides. VLS areas account for 19.64% of the study area and contains 1% of the total number of landslides. The bottom picture is rendered using elevation and hill shade. The red ellipse roughly delineates the areas with high susceptibility and contiguous distribution.

Table 1.
Sources and significances of the factors used in the analysis.
| No. | General category | Factors | Significance | Source and compilation method |
|---|---|---|---|---|
| 1 | Geologic | Distance to faults (dF) | Destruction of the stability of the rock mass structure | The fault structural lines came from the 1:200,000 geological map of Kunming. Using QGIS to compile Euclidean distance grid. |
| 2 | Lithology (Lth) | Lithological types of slope rock and soil | 1:200,000 geological map of Kunming | |
| 3 | Land cover | CLCD | The 30m annual land cover dataset in China | The 30m annual land cover dataset and its dynamics in China 2019 (CLCD) [19] |
| 4 | Land cover (LC) | The 10m land cover | ESA WorldCover 10 m 2020 v100 [28] | |
| 5 | Normalized difference vegetation index (NDVIlog) | China 30m Annual NDVI Maximum Dataset (2021) [29], as the log value. | ||
| 6 | Anthropogenic | Distance to roads (dRD) | Road cutting or vehicle vibration | Data come from OSM (OpenStreetMap, 2021). Using QGIS to compile the Euclidean distance grid. |
| 7 | Morphometric terrain parameters | Elevation (Elv) | Climate, vegetation and potential energy | NASADEM [30], the resolution of which is ~30m. |
| 8 | Aspect (Asp) | Solar insolation, flora and fauna distribution and abundance [1] | Compilation using SAGA GIS by NASADEM [30] | |
| 9 | Plan curvature (CPlan) | Converging, diverging flow, soil water content, and soil characteristics [1] | Compilation using SAGA GIS by NASADEM [30], with value ×106. | |
| 10 | Profile curvature (CProf) | Flow acceleration, erosion/deposition, and geomorphology [1] | Compilation using SAGA GIS by NASADEM [30], with value ×106. | |
| 11 | Tangential curvature (CTang) | Erosion/deposition [1] | Compilation using SAGA GIS by NASADEM [30], with value ×106. | |
| 12 | Topographic Position Index (TPI) | Quantifies topographic heterogeneity and erosion [31]. | Compilation using SAGA GIS by NASADEM [30] | |
| 13 | Terrain Ruggedness Index (TRI) | Quantifies topographic heterogeneity and erosion [32]. | Compilation using LSAT PM [4] by NASADEM [30] | |
| 14 | Roughness (Rou) | Quantifies topographic heterogeneity and erosion. | Compilation using LSAT PM [4] by NASADEM [30] | |
| 15 | Relative slope position (RSP) | Compilation using LSAT PM [4] by NASADEM [30] | ||
| 16 | Slope (SL) | Overland and sub-surface flow velocity [1] | Compilation using SAGA GIS by NASADEM [30] | |
| 17 | Water-related | Flow path length (FPL) | River erosion. | Compilation using SAGA GIS by NASADEM [30] |
| 18 | Flow Accumulation (FAlog) | Runoff velocity, runoff volume, and potential energy. | Compilation using SAGA GIS by NASADEM [30] as the log value. | |
| 19 | Height above nearest drainage (HAND) | River erosion, runoff velocity, runoff volume, and potential energy [33,34]. | Compilation using SAGA GIS by NASADEM [30] | |
| 20 | Horizontal HAND (HANDH) | River erosion, runoff velocity, runoff volume, and potential energy [33,34]. | Compilation using SAGA GIS by NASADEM [30] | |
| 21 | Vertical HAND (HANDV) | River erosion, runoff velocity, runoff volume, and potential energy [33,34]. | Compilation using SAGA GIS by NASADEM [30] | |
| 22 | Distance to channel network (dCN) | River erosion. | Compilation using SAGA GIS by NASADEM [30] | |
| 23 | Stream power index (SPIlog) | River erosion [35]. | Compilation using SAGA GIS by NASADEM [30] as the log value. | |
| 24 | Topographic wetness index (TWI) | Moisture content of soil [35,36,37] | Compilation using SAGA GIS by NASADEM [30] | |
| 25 | SAGA Wetness Index (TWISAGA) | Moisture content of soil [37,38] | Compilation using SAGA GIS by NASADEM [30] |
Table 3.
Statistical table of landslide susceptibility zoning area.
| Sub-regions | Area of sub-regions (%) | Total area of sub-regions (%) | Landslides(%) | Total landslides(%) |
|---|---|---|---|---|
| VHS | 5.05 | 5.05 | 50 | 50 |
| HS | 14.53 | 19.58 | 30 | 80 |
| MS | 28.23 | 47.81 | 15 | 95 |
| LS | 32.55 | 80.36 | 4 | 99 |
| VLS | 19.64 | 100 | 1 | 100 |
Table 4.
Thirteen factors with AUCs≥0.6 and their AUC values.

Table 5.
Factor classification with W+ ≥ 0.5

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Landslide Susceptibility Assessment Modeling in Yunnan Plateau Lake watershed: A Case Study for Dianchi Lake Watershed
Guangshun Bai
et al.
,
2023
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated








