Suppose that we have a non-lattice estimate $\widehat{w}$ of an unknown parameter $w\in R^q$ of a statistical model, based on a sample of size n. The distribution of a standard estimate is determined by the coefficients obtained by expanding its cumulants in powers of $n^{-1}$. In §2 we summarise the extended Edgeworth-Cornish-Fisher expansions of Withers (1984) for $\widehat{w}$ when $q=1$. Then we give the multivariate Edgeworth expansions to $O\left(n^{-2}\right)$. We show that the distribution of $X_n=n^{1/2}(\widehat{w}-w)$ has the form $Prob.(X_n\le x)\approx {\sum }_{r=0}^{\infty }{n}^{-r/2}{P}_r\left(x\right)$ where $P_0\left(x\right)={\Phi }_V\left(x\right),$ the normal distribution with $V=\left(k_1^{i_1{i}_2}\right)$, and for $r\ge 1,P_r\left(x\right)={\sum }_{k=1}^{3r}[P_{rk}\left(x\right):k-reven]$ where $P_{rk}\left(x\right)$ has $q^k$ terms, reducible using symmetry. Its density has a similarly form. We argue that these expansions may be valid even if $q=q_n\to \infty$ if $q_n/n^{1/6}$ is bounded.

§3 gives these expansions in complete detail when $q=2$.

In §4 we suppose that $q\ge 2$ and partition $X_n$ as $\left(\genfrac{}{}{0pt}{}{{\mathbf{X}}_{n1}}{{\mathbf{X}}_{n2}}\right)$ of dimensions $q_1\ge 1$ and $q_2\ge 1.$ We derive expansions for the conditional density and distribution of ${\mathbf{X}}_{n1}$ given ${\mathbf{X}}_{n2}$ to $O\left(n^{-2}\right)$ . §5 specialises to bivariate estimates.

§6 gives the extended Cornish-Fisher expansions for the quantiles of the conditional distribution when $q_1=1$. An example is the distribution of a sample mean given the sample variance.

Univariate estimates. Suppose that $\widehat{w}$ is a standard estimate of $w\in R$ with respect to n, typically the sample size. That is, $E\widehat{w}\to w$ as $n\to \infty$, and its rth cumulant can be expanded as where the cumulant coefficients $a_{rj}$ may depend on n but are bounded as $n\to \infty$, and $a_{21}$ is bounded away from 0. Here and below ≈ indicates an asymptotic expansion that need not converge. So (1) holds in the sense that where $y_n=O\left(x_n\right)$ means that $y_n/x_n$ is bounded in n. Withers (1984) extended Cornish and Fisher (1937) and Fisher and Cornish (1960) to give the distribution and quantiles of have asymptotic expansions in powers of $n^{-1/2}$:

where $\Phi \left(x\right)=Prob(N\le x),N\sim \mathcal{N}(0,1)$ is a unit normal random variable with density $\varphi \left(x\right)={(2\pi )}^{-1/2}{e}^{-x^2/2}$, and $h_r\left(x\right),{\overline{h}}_r\left(x\right),f_r\left(x\right),g_r\left(x\right)$ are polynomials in x and the standardized cumulant coefficients

and so on, where $H_k$ is the kth Hermite polynomial,

See Withers (1984) for $g_r,r\le 6,$, Withers (2000) for (6) and §6 for relations between $h_r,f_r,g_r$. Also,

For $r>1$, $b_r\left(x\right)$ is a polynomial of order only $r+2$, while ${\overline{h}}_r\left(x\right)$ is of order $3r$.

The original Edgeworth expansion was for $\widehat{w}$ the mean of n independent identically distributed random variables from a distribution with rth cumulant ${\kappa }_r$. So (1 ) holds with $a_{ri}={\kappa }_{r}I(i=r-1)$, and other $a_{ri}=0$. An explicit formula for its general term was given in Withers and Nadarajah (2009) using Bell polynomials.

Ordinary Bell polynomials. For a sequence $e=(e_1,e_2,\cdots ),$ the partial ordinary Bell polynomial ${\tilde{B}}_{rs}={\tilde{B}}_{rs}\left(e\right)$, is defined by the identity

where ${\delta }_{00}=1,{\delta }_{r0}=0$ for $r\ne 0.$ They are tabled on p309 of Comtet (1974). The complete ordinary Bell polynomial, ${\tilde{B}}_r\left(e\right)$ is defined in terms of S by

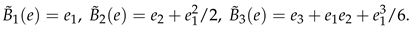
Multivariate estimates. Suppose that $\widehat{w}$ is a standard estimate of

$w\in R^p$ with respect to n. That is, $E\widehat{w}\to w$ as $n\to \infty$, and for $r\ge 1$,

$1\le i_1,\dots ,i_r\le p,$ the rth order cumulants of $\widehat{w}$ can be expanded as where the cumulant coefficients ${\overline{k}}_d^{1-r}=k_d^{i_1-i_r}$ may depend on n but are bounded as $n\to \infty$. So the bar replaces $i_j$ by j: ${\overline{k}}_0^1=w^{i_1},{\overline{k}}_1^{12}=k_1^{i_1{i}_2}.$ with density and distribution

V may depend on n, but we assume that $det\left(V\right)$ is bounded away from 0. Set

where for $r\le 3,{\overline{P}}_r^{1-k}$ is a function of ${\overline{k}}_e^{1-r}$ given for the 1st time in the appendix. In (13), (14) and below, we use the tensor summation convention of implicitly summing $i_1,\cdots ,i_r$ over their range $1,\cdots ,q$. We make ${\overline{P}}_r^{1-k}$ symmetric in $i_1,\cdots ,i_k$ using the operator $\mathcal{S}$ that symmetrizes over $i_1,\cdots ,i_k$:

The terms involving $\mathcal{S}$ are given in the Appendix A. By Withers and Nadarajah (2010b) or Withers (2024), $X_n$ has distribution and density

is the multivariate Hermite polynomial. For their dual form see Withers and Nadarajah (2014). By Withers (2020), for $i=\sqrt{-1}$, where $V^{i_1{i}_2}$ is the $(i_1,i_2)$ element of $V^{-1},$ and ${\overline{V}}^{j_1{j}_2}$ is the $(i_{j_1},i_{j_2})$ element of $V^{-1}.$ This gives ${\overline{H}}^{1-k}$ in terms of the moments of Y. For example

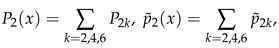
This gives the Edgeworth expansion for the distribution of $Y_n$ to $O\left(n^{-2}\right)$. See Withers (2024) for more terms.

For large q, $P_{rk},{\tilde{p}}_{rk}$ of (21) and (23) have $\sim q^{3r}$ terms. So if $q=q_n\to \infty$ and $M_{rn}=ma{x}_k\left|{\overline{P}}_r^{1-k}\right|$, then $n^{-r/2}(P_r\left(x\right),p_r\left(x\right)\sim M_{rn}{\nu }_n^r$ where ${\nu }_n=n^{-1/2}{q}_n^3$. So if for example $M_{rn}$ is bounded, then the Edgeworth series should converge if $q_n/n^{1/6}\to 0.$

The log density can be expanded as

See Withers and Nadarajah (2016). Also for $H_k\left(x\right)$ of (6),

${\tilde{p}}_{rk}$ and $P_{rk}$ have $q^k$ terms but many are duplicates. We now show how symmetry reduces this to $\sim \left(\genfrac{}{}{0pt}{}{q}{k}\right)$ terms. We use the multinomial coefficient $\left(\genfrac{}{}{0pt}{}{k}{a\cdots b}\right)=k!/a!\cdots b!$. For example $\left(\genfrac{}{}{0pt}{}{3}{111}\right)=6$.

Set $T_r^{i_1\cdots i_k}={\overline{P}}_r^{1-k}{\overline{H}}^{1-k}$ where tensor summation is not used. By (22), where all $i_j$ are distinct. Similarly we can write out ${\tilde{p}}_{rk}$ for $k=5,7,9.$ This reduces the number of terms in ${\tilde{p}}_{rk}$ from $q^k$ to $q+\left(\genfrac{}{}{0pt}{}{q}{2}\right)$ for $k=2$, to $q+q(q-1)+\left(\genfrac{}{}{0pt}{}{q}{3}\right)$ for $k=3$, to $q+q(q-1)+\left(\genfrac{}{}{0pt}{}{q}{2}\right)+q\left(\genfrac{}{}{0pt}{}{q}{2}\right)+\left(\genfrac{}{}{0pt}{}{q}{4}\right)$ for $k=4,$ and to $q+5\left(\genfrac{}{}{0pt}{}{q}{2}\right)+10\left(\genfrac{}{}{0pt}{}{q}{3}\right)+14\left(\genfrac{}{}{0pt}{}{q}{4}\right)+\left(\genfrac{}{}{0pt}{}{q}{6}\right)$ for $k=6.$

If we reinterpret $T_r^{i_1\cdots i_k}$ as ${\overline{P}}_r^{1-k}(-{\overline{\partial }}_1)\cdots (-{\overline{\partial }}_k){\Phi }_V\left(x\right)$, where again tensor summation is not used, then we can reinterpret the above expression for ${\tilde{p}}_{rk}$, as an expression for $P_{rk}\left(x\right)$. For example,

These results can be extended to Type B estimates, that is to $\widehat{w}$ with cumulant expansions not of type (11), but

We first give ${\tilde{p}}_{rk}$ of (22) for $r\le 3$, and then $P_{rk}\left(x\right)$ of (21). for ${\overline{P}}_r^{1-k}$ of (16), (17), where we use the dual notation,

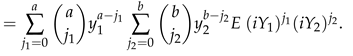
So $H_{k0}$ and $H_{0k}$ are given by (29) with $j=1$ and 2,

For more examples see Withers (2000). $P_r\left(1^b{2}^a\right)$ is just $P_r\left(1^a{2}^b\right)$ with 1 and 2 reversed. The other $P_r\left(1^a{2}^b\right)$ needed in (31) for ${\tilde{p}}_{rk}$ are as follows.

(18) and (22) now give the distribution and density of $X_n=n^{1/2}(\widehat{w}-w)$ to $O\left(n^{-2}\right)$. Set

Then $P_{rk}\left(x\right)$ of (21) is given by replacing $H_{ab}$ by $H_{ab}^{*}$ in the expressions above for ${\tilde{p}}_{rk}$. That is,

(18) and (21) now give $Prob(X_n\le x)$ to $O\left(n^{-2}\right)$ for $X_n=n^{1/2}(\widehat{w}-w)$.

For $q=q_1+q_2,q_1\ge 1,$ and $q_2\ge 1,$ partition $x,y=V^{-1}x,X_n=n^{1/2}(\widehat{w}-w)$ and $X\sim {\mathcal{N}}_q(0,V)$, as $\left(\genfrac{}{}{0pt}{}{{\mathbf{x}}_1}{{\mathbf{x}}_2}\right),\left(\genfrac{}{}{0pt}{}{{\mathbf{y}}_1}{{\mathbf{y}}_2}\right),\left(\genfrac{}{}{0pt}{}{{\mathbf{X}}_{n1}}{{\mathbf{X}}_{n2}}\right),\left(\genfrac{}{}{0pt}{}{{\mathbf{X}}_1}{{\mathbf{X}}_2}\right),$ where ${\mathbf{x}}_i,{\mathbf{y}}_i,{\mathbf{X}}_{ni}$ are vectors of length $q_i$. Partition $V,V^{-1}$ as $\left({\mathbf{V}}_{ij}\right),\left({\mathbf{V}}^{ij}\right)$ where ${\mathbf{V}}_{ij},{\mathbf{V}}^{ij}$ are $q_i\times q_j$.