Location via proxy:   [ UP ]  
[Report a bug]   [Manage cookies]                
Scribd
Upload
29 views

MITRES18 05S10 Linear Approx Newtons Method

This document discusses linear approximation and Newton's method for finding roots of functions. 1. It explains how the tangent line at a point x=a can be used to linearly approximate the value of a function f(x) near x=a. 2. It provides examples of using linear approximation to estimate values of exponential and polynomial functions. 3. It then introduces Newton's method, which uses successive linear approximations to iteratively find better estimates for roots of a function f(x).

Uploaded by

UnoShankar
Copyright
© Attribution Non-Commercial (BY-NC)
Available Formats
Download as PDF, TXT or read online on Scribd
29 views

MITRES18 05S10 Linear Approx Newtons Method

This document discusses linear approximation and Newton's method for finding roots of functions. 1. It explains how the tangent line at a point x=a can be used to linearly approximate the value of a function f(x) near x=a. 2. It provides examples of using linear approximation to estimate values of exponential and polynomial functions. 3. It then introduces Newton's method, which uses successive linear approximations to iteratively find better estimates for roots of a function f(x).

Uploaded by

UnoShankar
Copyright
© Attribution Non-Commercial (BY-NC)
Available Formats
Download as PDF, TXT or read online on Scribd
You are on page 1/ 3

Linear Approximation and Newtons Method

Linear Approximation and Newtons Method

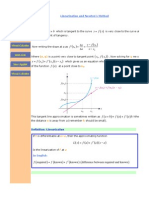
Start at x D a with known f .a/ D height and f .a/ D slope KEY IDEA f .a/ f .x/ f .a/ when x is near a x a

Tangent line has slope f .a/ Solve for f .x/ f .x/ f .a/ C .x a/f .a/

means approximately curve line near x D a

Examples of linear approximation to f .x/ 1. f .x/ D e x f .0/ D e 0 D 1 and f .0/ D e 0 D 1 are known at a D 0 Follow the tangent line e x 1 C .x 0/1 D 1 C x 1 C x is the linear part of the series for e x 2. f .x/ D x 10 and f .x/ D 10x 9 f .1/ D 1 and f .1/ D 10 known at a D 1 Follow the tangent line x 10 1 C .x 1/10 near x D 1 Take x D 1:1 .1:1/10 is approximately 1 C 1 D 2

Newtons Method (looking for x to nearly solve f .x/ D 0) f .x/ f .a/ x a f .a/ and f .a/ are again known Go back to f .a/

f .x/ exact x

Solve for x when f .x/ D 0 f .a/ Newton x x a f .a/ Line crossing near curve crossing

a Newton x

Linear Approximation and Newtons Method

Examples of Newtons Method Solve f .x/ D x 2 1:2 D 0 1. a D 1 gives f .a/ D 1 1:2 D :2 and f .a/ D 2a D 2 .:2/ 2 Tangent line hits 0 at x 1 D

Newtons x will be 1:1

2. For a better x; Newton starts again from that point a D 1:1 Now f .a/ D 1:12 1:2 D :01 and f .a/ D 2a D 2 :2 :01 2:2 The new tangent line has x 1:1 D

For this x; x 2 is very close to 1:2

Practice Questions 1. The graph of y D f .a/ C .x a/f .a/ is a straight At x D a the height is y D At x D a the slope is dy=dx D This graph is t t to the graph of f .x/ at x D a For f .x/ D x 2 at a D 3 this linear approximation is y D

2. y D f .a/ C .x a/f .a/ has y D 0 when x a D Instead of the curve f .x/ crossing 0, Newton has tangent line y crossing 0 f .x/ D x 3 8:12 at a D 2 has f .a/ D Newtons method gives x 2 D and f .a/ D 3a2 D

f .a/ D f .a/ This Newton x D 2:01 nearly has x 3 D 8:12: It actually has .2:01/3 D

MIT OpenCourseWare http://ocw.mit.edu

Resource: Highlights of Calculus


Gilbert Strang

The following may not correspond to a particular course on MIT OpenCourseWare, but has been provided by the author as an individual learning resource.

For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms.

You might also like