Location via proxy:   [ UP ]  
[Report a bug]   [Manage cookies]                
Scribd
Upload
49 views

Narrow-Band Frequency Modulation: Lecture #16, May 3, 2011

1. Narrow-band frequency modulation results in an FM signal with a narrow bandwidth. 2. The spectrum of an FM signal contains a carrier signal and an infinite number of sidebands spaced at multiples of the modulation frequency. 3. For small modulation indices, the FM signal can be approximated as the sum of the carrier and just one pair of sidebands at f_c ± f_m.

Uploaded by

deepam0187
Copyright
© © All Rights Reserved
Available Formats
Download as PDF, TXT or read online on Scribd
49 views

Narrow-Band Frequency Modulation: Lecture #16, May 3, 2011

1. Narrow-band frequency modulation results in an FM signal with a narrow bandwidth. 2. The spectrum of an FM signal contains a carrier signal and an infinite number of sidebands spaced at multiples of the modulation frequency. 3. For small modulation indices, the FM signal can be approximated as the sum of the carrier and just one pair of sidebands at f_c ± f_m.

Uploaded by

deepam0187
Copyright
© © All Rights Reserved
Available Formats
Download as PDF, TXT or read online on Scribd
You are on page 1/ 21

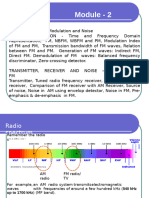
Narrow-band Frequency

Modulation
KEEE343 Communication Theory
Lecture #16, May 3, 2011
Prof. Young-Chai Ko
koyc@korea.ac.kr
Summary

Narrowband Frequency Modulation

Wideband Frequency Modulation


Narrow-Band Frequency Modulation

Narrow-Band FM means that the FM modulated wave has narrow


bandwidth.

Consider the single-tone wave as a message signal:

FM signal

Instantaneous frequency

Phase
m(t) = A
m
cos(2f
m
t)
f
i
(t) = f
c
+ k
f
A
m
cos(2f
m
t)
= f
c
+f cos(2f
m
t)

i
(t) = 2
Z
t
0
f
i
() d = 2

f
c
t +
f
2f
m
sin(2f
m
t)

= 2f
c
t +
f
f
m
sin(2f
m
t)
f = k
f
A
m

Denitions

Phase deviation of the FM wave

Modulation index of the FM wave:

Then, FM wave is

To be narrow-band FM, should be small.

For small compared to 1 radian, we can rewrite


=
f
f
m
s(t) = A
c
cos[2f
c
t + sin(2f
m
t)]
f
m
s(t) A
c
cos(2f
c
t) A
c
sin(2f
c
t) sin(2f
m
t)
s(t) = A
c
cos(2f
c
t) cos( sin(2f
m
t)) A
c
sin(2f
c
t) sin( sin(2f
m
t))

cos[ sin(2f
m
t)] 1, sin[ sin(2f
m
t)] sin(2f
m
t)

[Ref: Haykin & Moher, Textbook]

Consider the modulated signal


which can be rewritten as
where
and
Polar Representation from Cartesian
s(t) = a(t) cos(2f
c
t +(t))
s(t) = s
I
(t) cos(2f
c
t) s
Q
(t) sin(2f
c
t)
s
I
(t) = a(t) cos((t)), and, s
Q
(t) = a(t) sin((t))
a(t) =

s
2
I
(t) + s
2
Q
(t)

1
2
, and (t) = tan
1

s
Q
(t)
s
I
(t)

Approximated narrow-band FM signal can be written as

Envelope

Maximum value of the envelope

Minimum value of the envelope


s(t) A
c
cos(2f
c
t) A
c
sin(2f
c
t) sin(2f
m
t)
for small

a(t) = A
c

1 +
2
sin
2
(2f
m
t)

A
c

1 +
1
2

2
sin
2
(2f
m
t)

A
max
= A
c

1 +
1
2

A
min
= A
c

The ratio of the maximum to minimum value

Rewriting the approximated narrow-band FM wave is

Average power

Average power of the unmodulated wave


A
max
A
min
=

1 +
1
2

s(t) A
c
cos(2f
c
t) +
1
2
cos(2(f
c
+ f
m
)t)
1
2
A
c
cos(2(f
c
f
m
)t)
P
av
=
1
2
A
2
c
+

1
2
A
c

2
+

1
2
A
c

2
=
1
2
A
2
c
(1 +
2
)
P
c
=
1
2
A
2
c

Ration of the average power to the power of the unmodulated wave

Comparison with the AM signal

Approximated Narrow-band FM signal

AM signal
P
av
P
c
= 1 +
2
s(t) A
c
cos(2f
c
t) +
1
2
cos(2(f
c
+ f
m
)t)
1
2
A
c
cos(2(f
c
f
m
)t)
s
AM
(t) = A
c
cos(2f
c
t) +
1
2
A
c
{cos[2(f
c
+ f
m
)t)] + cos[2(f
c
f
m
)t]}
difference between the narrow-band FM and AM waves

Bandwidth of the narrow-band FM:

Phasor interpretation
2f
m
[Ref: Haykin & Moher, Textbook]

Angle

Using the power series of the tangent function such as


(t) = 2f
c
t +(t) = 2f
c
t + tan
1
( sin(2f
m
t))
tan
1
(x) x
1
3
x
3
+

Angle can be approximated as

Ideally, we should have

The harmonic distortion value is

The maximum absolute value of D(t) is


(t) 2f
c
t + sin(2f
m
t)
D(t) =

3
3
sin
3
(2f
m
t)
(t) 2f
c
t + sin(2f
m
t)
1
3

3
sin
3
(2f
m
t)
D
max
=

3
3

For example for


which is small enough for it to be ignored in practice.
= 0.3,
D
max
=
0.3
3
3
= 0.009 1%
Amplitude Distortion of Narrow-band FM

Ideally, FM wave has a constant envelope

But, the modulated wave produced by the narrow-band FM differ from


this ideal condition in two fundamental respects:

The envelope contains a residual amplitude modulation that varies


with time

The angle contains harmonic distortion in the form of third-


and higher order harmonics of the modulation frequency

i
(t)
f
m
Wide-Band Frequency Modulation

Spectral analysis of the wide-band FM wave


or
where is called complex envelope.
Note that the complex envelope is a periodic function of time with a
fundamental frequency which means
where
s(t) = A
c
cos[2f
c
t + sin(2f
m
t)]
s(t) = <[A
c
exp[j2f
c
t + j sin(2f
m
t)]] = <[ s(t) exp(j2f
c
t)]
s(t) = A
c
exp [j sin(2f
m
t)]
f
m
s(t) = s(t + kT
m
) = s(t +
k
f
m
)
T
m
= 1/f
m

Then we can rewrite

Fourier series form


where
s(t) =

X
n=
c
n
exp(j2nf
m
t)
c
n
= f
m
Z
1/(2f
m
)
1/(2f
m
)
s(t) exp(j2nf
m
t) dt
= f
m
A
c
Z
1/(2f
m
)
1/(2f
m
)
exp[j sin(2f
m
t) j2nf
m
t] dt
s(t) = s(t + k/f
m
)
= A
c
exp[j sin(2f
m
(t + k/f
m
))]
= A
c
exp[j sin(2f
m
t + 2k)]
= A
c
exp[j sin(2f
m
t)]

Dene the new variable:


Then we can rewrite

nth order Bessel function of the rst kind and argument

Accordingly
which gives
x = 2f
m
t
c
n
=
A
c
2
Z

exp[j( sin x nx)] dx

J
n
() =
1
2
Z

exp[j( sin x nx)] dx


c
n
= A
c
J
n
()
s(t) = A
c

X
n=
J
n
() exp(j2nf
m
t)

Then the FM wave can be written as

Fourier transform
which shows that the spectrum consists of an innite number of delta
functions spaced at for
s(t) = <[ s(t) exp(j2f
c
t)]
= <
"
A
c

X
n=
J
n
() exp[j2n(f
c
+ f
m
)t]
#
= A
c

X
n=
J
n
() cos[2(f
c
+ nf
m
)t]
S(f) =
A
c
2

X
n=
J
n
() [(f f
c
nf
m
) + (f +f
c
+nf
m
)]
f = f
c
nf
m
n = 0, +1, +2, ...
1. For different values of n
2. For small value of
6. The equality holds exactly for arbitrary
Properties of Single-Tone FM for Arbitrary Modulation
Index

J
n
() = J
n
(), for n even
J
n
() = J
n
(), for n odd
J
0
() 1,
J
1
()

2
J
n
() 0, n > 2

X
n=
J
2
n
() = 1
[Ref: Haykin & Moher, Textbook]
1. The spectrum of an FM wave contains a carrier component and and an innite
set of side frequencies located symmetrically on either side of the carrier at
frequency separations of ...
2. The FM wave is effectively composed of a carrier and a single pair of side-
frequencies at .
3. The amplitude of the carrier component of an FM wave is dependent on the
modulation index . The averate power of such as signal developed across a 1-
ohm resistor is also constant:
The average power of an FM wave may also be determined from
f
m
, 2f
m
, 3f
m
f
c
f
m

P
av
=
1
2
A
2
c
P
av
=
1
2
A
2
c

X
n=
J
2
n
()

You might also like