Location via proxy:   [ UP ]  
[Report a bug]   [Manage cookies]                
Scribd
Upload
1K views

Derivative Formulas

This document defines the derivatives of common functions like sine, cosine, exponential, and logarithmic functions. It also provides the derivative formulas for: - Constant functions, which have a derivative of 0 - The sum and difference of two functions - Power functions using the power rule - Products of functions using the product rule - Quotients of functions using the quotient rule - Composite functions using the chain rule

Uploaded by

Zhi Wei Chow
Copyright
© Attribution Non-Commercial (BY-NC)
Available Formats
Download as PDF, TXT or read online on Scribd
1K views

Derivative Formulas

This document defines the derivatives of common functions like sine, cosine, exponential, and logarithmic functions. It also provides the derivative formulas for: - Constant functions, which have a derivative of 0 - The sum and difference of two functions - Power functions using the power rule - Products of functions using the product rule - Quotients of functions using the quotient rule - Composite functions using the chain rule

Uploaded by

Zhi Wei Chow
Copyright
© Attribution Non-Commercial (BY-NC)
Available Formats
Download as PDF, TXT or read online on Scribd
You are on page 1/ 2

Calculus

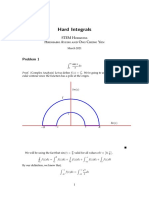
Derivative Formulas
[Definition of the Derivative of a Function f ]

f (x+ h)" f (x)


f '(x)= lim
h!0 h
[Definitions of f '(a) , the Derivative of f at x = a ]

f (a+ h)" f (a) f (x)" f (a)


f '(a)= lim = x!a
lim
h!0 h x"a
[Derivative of common functions]

d d
(D1.) (sin x) = cos x (D2.) (csc x) = !csc x " cot x
dx dx
d d
(D3.)
dx
(cos x) = !sin x (D4.)
dx
(sec x) = sec x ! tan x
d d
(D5.) ( tan x) = sec 2 x (D6.)
dx
(cot x) = !csc 2 x
dx

d d 1
(D7.)
dx
( e )= e
x x
(D8.)
dx
(ln x) =
x
d d 1
(D9.)
dx
( b )= b
x x
! ln b (D10.)
dx
( log b x) =
x !ln b
d 1 d 1
(D11.)
dx
( sin!1 x) = (D12.)
dx
( csc!1 x) = !
1! x 2 | x | x 2 !1

d 1 d 1
(D13.)
dx
( cos!1 x) = ! (D14.)
dx
( sec!1 x) =
1! x 2 | x | x 2 !1

d 1 d 1
(D15.)
dx
( tan!1 x) =
1+ x 2
(D16.)
dx
( cot!1 x) = !
1+ x 2

Produced by Steve Chow, 2009 1


[Differentiation Rules]

 [Constant Function]
If f (x)= c for some constant c, then
f '(x)= 0
 [Sum/Difference Rule]
If F(x)= f (x)± g(x) , then
F '(x)= f '(x)± g '(x)
 [Power Rule]
If f (x) = x n for all real number n, then

f '(x) = n ! x n"1
 [Product Rule]
If F(x) = f (x) ! g(x) , then
F '(x) = f (x) ! g '(x) + g(x) ! f '(x)
 [Quotient Rule]
f (x)
If F(x) = , then
g(x)
g(x) ! f '(x) " f (x) ! g '(x)
F '(x) = 2
#$ g(x) %&

 [Chain Rule]

(
If F(x) = f g(x) , then )
( )
F '(x) = f ' g(x) ! g '(x)
Produced by Steve Chow, 2009 2

You might also like