Location via proxy:   [ UP ]  
[Report a bug]   [Manage cookies]                
Scribd Logo
Upload

Welcome to Scribd!

  • 228 views

    Pier Footing

    Uploaded by

    Mathurathipan Rajendraseelan
    This document provides the results of a design analysis for a rigid round pier foundation subjected to vertical, horizontal, and moment loads. Key results include: 1. The pier has a total length of 2.06m and embedment depth of 2.06m, satisfying the requirement of L/D<=10. 2. The maximum shear in the pier is 12.29kN and maximum moment is 12.09kNm. 3. Stresses in the pier concrete from axial, flexural, shear, and combined forces were calculated and satisfy code requirements.

    Copyright:

    Attribution Non-Commercial (BY-NC)
    Download as PDF, TXT or read online from Scribd

    Pier Footing

    Uploaded by

    Mathurathipan Rajendraseelan
    228 views2 pages
    This document provides the results of a design analysis for a rigid round pier foundation subjected to vertical, horizontal, and moment loads. Key results include: 1. The pier has a total length of 2.06m and embedment depth of 2.06m, satisfying the requirement of L/D<=10. 2. The maximum shear in the pier is 12.29kN and maximum moment is 12.09kNm. 3. Stresses in the pier concrete from axial, flexural, shear, and combined forces were calculated and satisfy code requirements.

    Original Description:

    Footing

    Copyright

    © Attribution Non-Commercial (BY-NC)

    Available Formats

    PDF, TXT or read online from Scribd

    Did you find this document useful?

    Is this content inappropriate?

    This document provides the results of a design analysis for a rigid round pier foundation subjected to vertical, horizontal, and moment loads. Key results include: 1. The pier has a total length of 2.06m and embedment depth of 2.06m, satisfying the requirement of L/D<=10. 2. The maximum shear in the pier is 12.29kN and maximum moment is 12.09kNm. 3. Stresses in the pier concrete from axial, flexural, shear, and combined forces were calculated and satisfy code requirements.

    Copyright:

    Attribution Non-Commercial (BY-NC)
    Download as PDF, TXT or read online from Scribd
    Download as pdf or txt
    228 views2 pages

    Pier Footing

    Uploaded by

    Mathurathipan Rajendraseelan
    This document provides the results of a design analysis for a rigid round pier foundation subjected to vertical, horizontal, and moment loads. Key results include: 1. The pier has a total length of 2.06m and embedment depth of 2.06m, satisfying the requirement of L/D<=10. 2. The maximum shear in the pier is 12.29kN and maximum moment is 12.09kNm. 3. Stresses in the pier concrete from axial, flexural, shear, and combined forces were calculated and satisfy code requirements.

    Copyright:

    Attribution Non-Commercial (BY-NC)
    Download as PDF, TXT or read online from Scribd
    Download as pdf or txt
    You are on page 1of 2

    ABC CONSULTING ENGINEERS

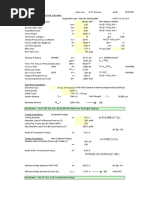
    For Free-Top (Unconstrained) Rigid Round Piers Using PCA / Czerniak Method Subjected Vertical Load, Horizontal Load, and/or Moment Job Name : Subject : Pier Footing Design Job Number: Designer: RM Input Data: Pier Data: Pier Foundation Diameter, D = Pier Height Above Soil, h1 = Concrete Strength, f'c = Soil Data: Unit Weight of Soil, = Angle of Internal Friction, = Depth to Resisting Surface, h2 = Allow. Soil Bearing Pressure, Pa = Pier Loadings: Axial Load, Pv = Horizontal Load, Ph = Distance from Ph to Top/Pier, H = Externally Applied Moment, M = Results: 1.00 3.00 4.00 0.00
    kN kN m kNm Pier Resisting Surface

    Pv=1 kN

    0.60 0.00 20.00

    m m Mpa

    M=0 kNm Ph=3 kN

    20.00 30.00 0.00 100.00

    kN/m3 deg. m kN/m2

    H=4m h1=0m

    Ground Line

    h2=0m

    L=2.06m

    D=0.6m

    Pier Embedment and Total Length: Nomenclature Ho = 5.00 kN/m Ho = Ph/D 20.00 kN-m/m Mo = (M+Ph*(H+h1+h2))/D Mo = E= 4.00 m E = Mo/Ho Kp = 3.00 Kp = TAN^2(45+/2) (passive soil pressure coefficient) R= 60.00 kN/m2/m R = Kp* (passive soil resistance/ft. depth) L= 2.06 m L = solution of cubic equation: L^3-(14*Ho/R)*L-(19*Mo/R)=0 L/D = 3.43 L/D <= 10 for valid short, rigid pier analysis L/D<=10, O.K. Lt = 2.06 m Lt = h1+h2+L (total length) Pier Side Soil Pressures: a= 1.42 m Pc = 42.47 kN/m2 Pc(allow) = 42.50 kN/m2 Pt = 111.75 kN/m2 Pt(allow) = 123.54 kN/m2 Pier End Bearing Pressure: m2 Af = 0.28 Wf = 0.09 kN Pv = 1.09 kN kN/m2 P(bot) = 3.85

    a = L*(4*E/L+3)/(6*E/L+4) ("pivot" point from top of resisting surface) Pc = 1.18*(4*Mo+3*Ho*L)^2/(L^2*(3*Mo+2*Ho*L)) Pc(allow) = Pp*(a/2) Pc(allow)>=Pc, O.K. Pt = 9.42*(2*Mo+Ho*L)/L^2 Pt(allow) = Pp*L Pt(allow)>=Pt, O.K.

    Af = *D^2/4 (pier base area) Wf = (Af*Lt)*0.150 (pier weight) Pv = Pv+Wf (total vertical load) P(bot) = Pv/Af

    Pa>=P(bot), O.K.

    (continued)

    Pier Shear and Moment: Maximum Shear: V(max) = 12.29 kN Maximum Moment: M(max) = 12.09

    (located at distance = a, from top of resisting surface) V(max) = ABS(Ho*D*(1-3*(4*E/L+3)*(a/L)^2+4*(3*E/L+2)*(a/L)^3) (located at distance = a/2, from top of resisting surface) M(max) = Ho*D*L*(E/L+a/2/L-(4*E/L+3)*(a/2/L)^3+(3*E/L+2)*(a/2/L)^4)

    kNm

    Pier Plain Concrete Stresses: Axial Compressive Stress: fa = 0.02 Mpa

    fa = (Pv+*D^2/4*(h1+h2+a/2)*24)/(*(D)^2/4)/1000

    Flexural Tension/Compression Stress: fb = 0.57 Mpa fb = M(max)/(*(D)^3/32)/1000 Combined Compression Stress: fc = 0.59 Mpa Fc(allow) = 12.00 Mpa Combined Tension Stress: ft = 0.55 Mpa Ft(allow) = 1.74 Mpa Shear Stress: fv = 0.04 Fv(allow) = 1.63 (AS 3600-2009 Clause 3.1.1.1 , = 0.6 - Table 2.2.2) fc = fb+fa (compression) Fc(allow) = *fc' Fc(allow)>=fc, O.K. (AS 3600-2009 Clause 3.1.1.3 , = 0.6 - Table 2.2.2) ft = fb-fa (tension) Ft(allow) = *0.36*(fc')0.5*1.8 Ft(allow)>=ft, O.K. (AS 3600-2009 Clause 8.2.7.1 , = 0.6 - Table 2.2.2) fv = V(max)/((*(D)^2/4)*1000) (shear) Fv(allow) = *(f'c)1/3 Fv(allow)>=fv, O.K.

    Mpa Mpa

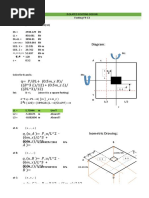
    Applied Lateral Load and Resistance of Pole/Foundation Reference: "Resistance to Overturning of Single, Short Piles" - by Eli Czerniak ASCE Journal of the Struct. Div., Vol. 83, No. ST2, Paper 1188, Mar. 1957
    Ph Embedment depth, L, is solution of: L^3-(14*Ho/R)*L-(19*Mo/R) = 0 E Resisting Surface Mo Ho a 2 a L Ground Line

    R*L

    Pc

    Pt

    V(max)

    M(max)

    Applied Load

    Pole/Fdn. Rotation

    Unit Resist. Available

    Pressure Diagram

    Shear Diagram

    Moment Diagram

    You might also like