Design Rotating Mahcines

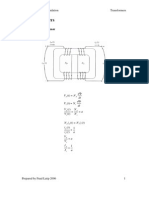
GENERAL CONCEPTS AND CONSTRAINTS IN DESIGN OF ROTATING MACHINES The purpose of this section is to try to relate the rating
of rotating machines to their main dimensions. Main dimensions: The armature diameter D and armature core length L are known as the main dimensions of a rotating machine. Total Loading Total magnetic loading: The total flux around the armature periphery at the air gap is called the total magnetic loading. Total magnetic loading = p. Total electrical Loading: The total number of ampere conductors around the armature periphery is called the total electric loading. Total electric loading = Iz.Z Specific loading: Two types of loading are specified which are the starting point in the design of rotating electrical machines. 1. Specific magnetic loading: The average flux density over the air gap of a machine is known as specific magnetic loading.
2. Specific electric loading: The number of armature ampere conductors per meter of armature periphery at the air gap is known as specific electric loading.
Output Equation: The output of a machine can be expressed in terms of its main dimensions, specific magnetic and electric loadings and speed; the equation describing this relationship is known as Output Equation. The output equations of the more important machines are given below: 1. DC Machines: power developed by armature in kW Pa = generated emf X armature current X 10-3 = EIa X10-3 But E=Znp/a Pa = Zn(p/a). Ia X10-3 = (p)( IaZ/a)n X10-3 = (p)( IzZ)n X10-3 Hence Pa = total magnetic loading X total electric loading X speed in rps X 10-3 Therefore, basically the output of a d.c. machine is determined by the total loadings. Pa = (specific magnetic loading X DL)(specific electric loading X D)X speed in rps X 10-3 Pa = (Bav X DL)(ac X D)X speed in rps X 10-3 = (2 Bav ac X 10-3)D2Ln = C0D2Ln Where C0= 2 Bav ac X 10-3 The above equation is known as output equation and C0 is defined as the output coefficient. 2. AC machine: consider an m phase machine having one circuit per phase, kA rating of machine
Q = number of phase X output voltage per phase X current per phase X 10-3 = m Eph Iph X 10-3 Terminal voltage of each phases may be taken equal to the induced emf per phase. We have, Induced emf per phase Eph =4.44 f Tph Kw Hence Q = mX 4.44 f Tph Kw Iph X 10-3 But f=pns/2 Therefore we can write Q = mX 4.44 (pns/2) Tph Kw Iph X 10-3 Now current in each conductor Iz = I ph Total number of armature conductors Z= number of phases X ( 2 X turns per phase) = 2 m Tph Hence total electric loading = Iz Z = 2 m Iph Tph hence, Q= 1.11 Kw (total magnetic loading) ( total electric loading) (synchronous speed) x 10-3 Q= 1.11 Kw (specific magnetic loading X DL)(specific electric loading X D) (synchronous speed) x 10-3 Q= (1.11 2Kw Bav ac X 10-3)D2Lns = (11 Kw Bav ac X 10-3)D2Lns = C0 D2Lns Where C0 =11 Kw Bav ac X 10-3, is defined as the output coefficient for an a.c. machine. Factors affecting Size of rotating machine: Examining output equation of the d.c. and a.c. machines it is observed that product D2L will decrease with increase of speed and/or increase of output co-efficient. Thus the volume of active parts of a rotating machine is (/4) D2L and evidently therefore the volume of active parts and hence the size ande the cost of the machine decreases with increase in speed and/or increase in the value of output co-efficient. Hence following factors affects the size of the machine: 1. Speed: it is clear from output equation of the machine that the volume of active parts varies inversely as the speed. Thus for the same output a machine designed with greater speed will have smaller size and hence lesser cost s compared to a machine designed with smaller speed. Therefore whenever a choice has to be made the highest practical speed rating should be selected. However, in special circumstances, the maximum speed may be limited by mechanical stresses in the armature materials. 2. Output coefficient: from the output equation of the machine it is clear that the volume of active parts I inversely proportional to the value of output co-efficient C0. Thus an increase in the value of C0 results in reduction in size and cost of machine and so looking from the economics point of view the value of output co-efficient should be as high as possible. Since the output coefficient is proportional to product of specific magnetic and specific electric loadings we conclude that the size and hence also the cost of machine decreases if increased values of specific magnetic and specific electric loading are used. How much high they should be pushed is decided by the designer by analysuing the effect of increased loadings on performance characteristics of machine as the cost of machine is not the only important aspect of a machine design.

Design Rotating Mahcines

Uploaded by

Copyright:

Available Formats

Design Rotating Mahcines

Uploaded by

Document Information

Original Description:

Original Title

Copyright

Available Formats

Share this document

Share or Embed Document

Sharing Options

Did you find this document useful?

Is this content inappropriate?

Copyright:

Available Formats

Design Rotating Mahcines

Uploaded by

Copyright:

Available Formats

GENERAL CONCEPTS AND CONSTRAINTS IN DESIGN OF ROTATING MACHINES The purpose of this section is to try to relate the rating

You might also like