Oliver Knill, Harvard Summer School, 2010

Chapter 4. Extrema and Double integrals

Section 4.1: Extrema, second derivative test
An important problem in multi-variable calculus is to extremize functions f(x, y) of two vari-
ables. As in one dimensions, in order to look for maxima or minima, we consider points, where
the derivative is zero.
A point (a, b) in the plane is called a critical point of a function f(x, y) if f(a, b) = 0, 0.
Critical points are candidates for extrema because at critical points, all directional derivatives
D
v
f = f v are zero.
Note that that we do not include points, where f or its derivative is not dened in the set of
critical points. We usually assume that a function is arbitrarily often dierentiable. Points
where the function is not smooth are part of the boundary of the region and would have to be
studied seperatly.
Examples:
1) f(x, y) = x
4
+ y
4
4xy + 2. The gradient is f(x, y) = 4(x
3
y), 4(y
3
x) with critical
points (0, 0), (1, 1), (1, 1).
2) f(x, y) = sin(x
2
+ y) + y. The gradient is f(x, y) = 2xcos(x
2
+ y), cos(x
2
+ y) + 1. For
a critical points, we must have x = 0 and cos(y) + 1 = 0 which means + k2. The critical
points are at (0, ), (0, 3), ....
3) The graph of f(x, y) = (x
2
+ y
2
)e
x
2
y
2
looks like a volcano. The gradient f = 2x
2x(x
2
+ y
2
), 2y 2y(x
2
+ y
2
)e
x
2
y
2
vanishes at (0, 0) and on the circle x
2
+ y
2
= 1. There is
a continuum of critical points.
4) The function f(x, y) = y
2
/2 g cos(x) is the energy of the pendulum. We have f =
(y, g sin(x)) = (0, 0 for x = 0, , 2, ..., y = 0. These points are equilibrium points, where
the pendulum is at rest.
5) The function f(x, y) = a log(y)by +c log(x)dx is left invariant by the ow of the Volterra
Lodka dierential equation x = axbxy, y = cy+dxy. The point (c/d, a/b) is a critical point.
6) The function f(x, y) = [x[ + [y[ is smooth on the rst quadrant. It does not have critical
points there. The function has a minimum at (0, 0) but it is not in the domain, where f and
f are dened.
For functions in one dimension, we needed f

(x) = 0, f

(x) > 0 to have a local minimum,

f

(x) = 0, f

(x) < 0 for a local maximum. If f

(x) = 0, f

(x) = 0, then the critical point was

undetermined and could be a maximum like for f(x) = x
4
, or a minimum like for f(x) = x
4
1
or a at inection point like for f(x) = x
3
.
Let now f(x, y) be a function of two variables with a critical point (a, b). Dene D = f
xx
f
yy
f
2
xy
.
It is called the discriminant. You might want to remember it with the help of the Hessian
matrix H =

f
xx
f
xy
f
yx
f
yy

because the discriminant is the determinant of H. Here is the

important second derivative test.
Assume (a, b) is a critical point for f(x, y).
If D > 0 and f
xx
(a, b) > 0 then (a, b) is a local minimum.
If D > 0 and f
xx
(a, b) < 0 then (a, b) is a local maximum.
If D < 0 then (a, b) is a saddle point.
In the case D = 0, we would need higher derivatives to determine the nature of the critical point.
Example: The function f(x, y) = x
3
/3x(y
3
/3y) has a graph which looks like a napkin.
It has the gradient f(x, y) = x
2
1, y
2
+1. There are 4 critical points (1, 1),(1, 1),(1, 1)
and (1, 1). The Hessian matrix which includes all partial derivatives is H =

2x 0
0 2y

.
For (1, 1) we have D = 4 and so a saddle point,
For (1, 1) we have D = 4, f
xx
= 2 and so a local maximum,
For (1, 1) we have D = 4, f
xx
= 2 and so a local minimum.
For (1, 1) we have D = 4 and so a saddle point. The function has a local maximum, a
local minimum as well as 2 saddle points.
To determine the maximum or minimum of f(x, y) on a domain, determine all critical points in
the interior the domain, and compare their values with maxima or minima at the bound-
ary. We will see next time how to get extrema on the boundary.
Example: Find the maximum of f(x, y) = 2x
2
x
3
y
2
on y 1. With f(x, y) = 4x
3x
2
, 2y), the critical points are (4/3, 0) and (0, 0). The Hessian is H(x, y) =

4 6x 0
0 2

.
At (0, 0), the discriminant is 8 so that this is a saddle point. At (4/3, 0), the discriminant is 8
and H
11
= 4/3, so that (4/3, 0) is a local maximum. We have now also to look at the boundary
y = 1 where the function is g(x) = f(x, 1) = 2x
2
x
3
1. Since g

(x) = 0 at x = 0, 4/3,
2
where 0 is a local minimum, and 4/3 is a local maximum on the line y = 1. Comparing
f(4/3, 0), f(4/3, 1) shows that (4/3, 0) is the global maximum.
As in one dimensions, knowing the critical points helps to understand the function. Critical
points are also physically relevant. Examples are congurations with lowest energy. Many
physical laws are based on the principle that the equations are critical points. Newton equa-
tions in Classical mechanics are an example: a particle of mass m moving in a eld V along a
path : t r(t) extremizes the integral S() =

b
a
mr

(t)
2
/2 V (r(t)) dt among all possible
paths. Critical points satisfy the Newton equations mr

(t)/2 V (r(t)) = 0.
Why is the second derivative test true? Assume f(x, y) has the critical point (0, 0) and is a
quadratic function satisfying f(0, 0) = 0. Then
ax
2
+ 2bxy + cy
2
= a(x +
b
a
y)
2
+ (c
b
2
a
)y
2
= a(A
2
+ DB
2
)
with A = (x+
b
a
y), B = b
2
/a
2
and discriminant D. You see that if a = f
xx
> 0 and D > 0 then
c b
2
/a > 0 and the function has positive values for all (x, y) ,= (0, 0). The point (0, 0) is a
minimum. If a = f
xx
< 0 and D > 0, then c b
2
/a < 0 and the function has negative values
for all (x, y) ,= (0, 0) and the point (x, y) is a local maximum. If D < 0, then the function can
take both negative and positive values. A general smooth function can be approximated by a
quadratic function near (0, 0).
Sometimes, we want to nd the overall maximum and not only the local ones. A point (a, b) in
the plane is called a global maximum of f(x, y) if f(x, y) f(a, b) for all (x, y). For example,
the point (0, 0) is a global maximum of the function f(x, y) = 1 x
2
y
2
. Similarly, we call
(a, b) a global minimum, if f(x, y) f(a, b) for all (x, y).
Problem: Does the function f(x, y) = x
4
+y
4
2x
2
2y
2
have a global maximum or a global
minimum? If yes, nd them.
Solution: the function has no global maximum. This can be seen by restricting the func-
tion to the x-axis, where f(x, 0) = x
4
2x
2
is a function without maximum. The function
has four global minima however. They are located on the 4 points (1, 1). The best way
to see this is to note that f(x, y) = (x
2
1)
2
+(y1)
2
2 which is minimal when x
2
= 1, y
2
= 1.
Here is a curious remark: let f(x, y) be the height of
an island. Assume there are only nitely many critical
points on the island and all of them have nonzero de-
terminant. Label each critical point with a +1 if it is
a maximum or minimum, and with 1 if it is a sad-
dle point. Sum up all these number and you will get 1,
independent of the function. This property is an exam-
ple of an index theorem, a prototype for important
theorems in physics and mathematics.
Section 4.2: Extrema with constraints
We aim now to nd maxima and minima of a function f(x, y) in the presence of a constraint
g(x, y) = 0. You can see that a necessary condition for a critical point is that the gradients of f
and g are parallel because otherwise, we can go along the level curve of g and get a nonzero di-
rectional derivatives. The condition of having parallel gradients, leads to a system of equations
3
which are called the Lagrange equations f(x, y) = g(x, y), g(x, y) = 0. These are three
equations for the three unknowns x, y, . The variable is called the Lagrange multiplier.
Given a function f(x, y) of two variables and a level curve g(x, y) = c. Find the extrema of f
on the curve. You see that at places, where the gradient of f is not parallel to the gradient
of g, the function f changes when we change position on the curve g = c. Therefore, we must
have a solution of three equations
f(x, y) = g(x, y), g(x, y) = c
to the three unknowns (x, y, ). Additionally we must check points with g(x, y) = (0, 0)
because also then the gradients are parallel.
Example: To nd the shortest distance from the origin to the curve x
6
+3y
2
= 1, we extremize
f(x, y) = x
2
+ y
2
under the constraint g(x, y) = x
6
+ 3y
2
1 = 0.
Solution: f = 2x, 2y, g = 6x
5
, 6y. The Lagrange equations f = g lead to the
system 2x = 6x
5
, 2y = 6y, x
6
+ 3y
2
1 = 0. We get = 1/3, x = x
5
, so that either x = 0 or
1 or 1. From the constraint equation, we obtain y =

(1 x
6
)/3. So, we have the solutions
(0,

1/3) and (1, 0), (1, 0). To see which is the minimum, just evaluate f on each of the
points. We see that (0,

1/3) are the minima.

Constrained optimization problems work also in more than 2 dimensions. For example, if
f(x, y, z) is a function of three variables and g(x, y, z) = c is a surface, we solve the system of
4 equations
f(x, y, z) = g(x, y, z), g(x, y, z) = c
to the 4 unknowns (x, y, z, ). If we want to extremize f(x, y, z) under two constraints g(x, y, z) =
c and h(x, y, z) = d, we have a system of 5 equations for 5 unknowns:
4
f(x, y, z) = g(x, y, z) + h(x, y, z), g(x, y, z) = c, h(x, y, z) = d
Example: Extrema of f(x, y, z) = z on the sphere g(x, y, z) = x
2
+ y
2
+ z
2
= 1 are ob-
tained by calculating the gradients f(x, y, z) = (0, 0, 1), g(x, y, z) = (2x, 2y, 2z) and solving
(0, 0, 1) = f = g = (2x, 2y, 2z), x
2
+ y
2
+ z
2
= 1. = 0 is excluded by the third
equation 1 = 2z so that the rst two equations 2x = 0, 2y = 0 give x = 0, y = 0. The 4th
equation gives z = 1 or z = 1. The extrema are the north pole (0, 0, 1) (maximum) and the
south pole (0, 0, 1) (minimum).
Example: Consider a dice showing i with probability p
i
, where i = 1, ..., 6. The entropy
of the probability distribution is dened as S( p) =

6
i=1
p
i
log(p
i
). Find the distribution p
which maximizes entropy under the constrained g( p) =

6
i=1
p
i
= 1.
Solution: f = (1 log(p
1
), . . . , 1 log(p
n
)), g = (1, . . . , 1). The Lagrange equations
are 1 log(p
i
) = , p
1
+ ... + p
6
= 1, from which we get p
i
= e
(+1)
. The last equation
1 =

i
exp(( + 1)) = 6 exp(( + 1)) xes = log(1/6) 1 so that p
i
= 1/6. The
distribution, where each event has the same probability is the distribution of maximal entropy.
Maximal entropy means least information content. A dice which is xed (asymmetric weight
distribution for example) allows a cheating gambler to gain prot. Cheating through asymmet-
ric weight distributions can be avoided by making the dices transparent.
Example: You manufacture cylindrical soda cans of height h and radius r. You want for
a xed volume V (r, h) = hr
2
= 1 a minimal surface area A(r, h) = 2rh + 2r
2
. With
x = h, y = r, you need to optimize f(x, y) = 2xy + 2y
2
under the constrained g(x, y) =
xy
2
= 1. Calculate f(x, y) = (2y, 2x + 4y), g(x, y) = (y
2
, 2xy). The task is to solve
2y = y
2
, 2x + 4y = 2xy, xy
2
= 1. The rst equation gives y = 2. Putting that in the
second one gives 2x + 4y = 4x or 2y = x. The third equation nally reveals 2y
3
= 1 or
y = 1/(2)
1/3
, x = 2(2)
1/3
. This means h = 0.54.., r = 2h = 1.08.
Remark. Other factors can inuence the shape. For example, the can has to withstand a
pressure up to 100 psi.
The Lagrange equations f(x, y) = g(x, y), g(x, y) = c do not give all the extrema. We
can also have g(x, y) = (0, 0). The parallel condition also could have been written as
f(x, y) = g(x, y), f(x, y) = x
2
+ (y 1)
2
, g(x, y) = x
2
y
3
. The function f has a lo-
cal maximum 1 at (0, 0) under the constraint g(x, y) = 0 but the Lagrange equations do not
nd it. The problem is that the gradient of g vanishes. g is technically parallel to f but
there is no such that f = g at this point. The reason for this mistake (which is present
in virtually all calculus text books), is that parallel of the two gradient is not equivalent to
f = g but can also mean f = g with = 0.
Can we avoid Lagrange? We could extremize f(x, y) under the constraint g(x, y) = 0 by nding
y = y(x) from the later and extremizing the 1D problem f(x, y(x)).
Example: To extremize f(x, y) = x
2
+ y
2
with constraint g(x, y) = x
4
+ 3y
2
1 = 0, solve
y
2
= (1 x
4
)/3 and minimize h(x) = f(x, y(x)) = x
2
+ (1 x
4
)/3. h

(x) = 0 gives x = 0. The

nd the maximum (1, 0), we had to maximize h(x) on [1, 1], which occurs at 1.
Sometimes, Lagrange could be avoided:
Extremize f(x, y) = x
2
+ y
2
under the constraint g(x, y) = p(x) + p(y) = 1, where p is
a complicated function in x which satises p(0) = 0, p

(1) = 2 The Lagrange equations

5
2x = p

(x), 2y = p

(y), p(x) + p(y) = 1 can be solved: with x = 0, y = 1, = 1, how-

ever, we can not solve g(x, y) = 1 for y. Substitution fails:
In general, the Lagrange method is more powerful.
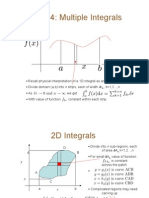
Section 4.3: Double integrals
Lets rst review integration in one dimensions. If f(x) is a continuous function, then

b
a
f(x) dx
is dened as a limit of the Riemann sum f
n
(x) =

x
k
[a,b]
f(x
k
)x for n with x
k
= k/n
and x = 1/n. This Riemann integral divided by [b a[ is the average of f on [a, b]. The
integral

b
a
f(x) dx can be interpreted as an signed area under the graph of f, which can be
negative too. If f(x) = 1, the integral is the length of the interval. The function F(x) =

x
a
f(y) dy is called an anti-derivative of f. The fundamental theorem of calculus states
F

(x) = f(x). This allows to compute integrals by inverting dierentiation. Dierentiation

rules like the Leibniz rule become integration rules like integration by part, the chain rule
becomes partial integration. Note that unlike the derivative, anti-derivatives can not always
be expressed in terms of known functions. An example is: F(x) =

x
0
e
t
2
dt. Often, the anti-
derivative can be found: Example: f(x) = cos
2
(x) = (cos(2x) + 1)/2, F(x) = x/2 sin(2x)/4.
Fx
FxdxFx
dx
If f(x, y) is a continuous function of two variables on a region R, the integral

R
f(x, y) dxdy
can be dened as the limit

i,j,xi,jR
f(x
i
, y
j
)xy with x
i,j
= (i/n, j/n) when n goes to
innity. If f(x, y) = 1, then the integral is the area of the region R. The integral divided by
the area of R is the average value of f on R. For many regions, the integral can be calculated
as a double integral

b
a
[

d(x)
c(x)
f(x, y) dy] dx.
6
One can interpret

R
f(x, y) dydx as the signed volume of solid below the graph of f and
above R in the x y plane. As in 1D integration, the volume of the solid below the xy-plane
is counted negatively.
Example: Calculate

R
f(x, y) dxdy, where f(x, y) = 4x
2
y
3
and where R is the rectangle
[0, 1] [0, 2].

1
0
[

2
0
4x
2
y
3
dy] dx =

1
0
[x
2
y
4
[
2
0
] dx =

1
0
x
2
(16 0) dx = 16x
3
/3[
1
0
=
16
3
.
Fubinis theorem states that we can interchange the order of integration if we integrate over
a rectangle:

b
a

d
c
f(x, y) dxdy =

d
c

b
a
f(x, y) dydx.
This can be seen by approximate both sides with a Riemann sum, where x = y = 1/n. We
have the identity

xi[a,b]

yj[c,d]
f(x
i
, y
j
) yy =

yj[c,d]

xi[a,b]
f(x
i
, y
j
) xx .
Now take the limit n .
Fubinis theorem only holds for rectangles. We extend the class of regions now to so called
Type I and Type II regions:
If the region satises a x b and is bounded by the
graphs of two functions c(x) and d(x), it is called of type
I. One can write the region as
R = (x, y) [ a x b c(x) y d(x) .
An integral over such a region is an iterated integral which
is:

R
f dA =

b
a

d(x)
c(x)
f(x, y) dydx .
b a
cx
dx
7
If the region is bound between the graphs of the functions
a(y) and b(y), the region is called of type II. One can write
the region as
R = (x, y) [ c y d, a(y) x b(y) .
An integral over such a region is an iterated integral:

R
f dA =

d
c

b(y)
a(y)
f(x, y) dxdy .
d
c
ay
by
Example: Integrate f(x, y) = x
2
over the region bounded
above by sin(x
3
) and bounded below by the graph of
sin(x
3
) for 0 x . The value of this integral has
a physical meaning. It is a moment of inertia. We will
come back to that next week.

1/3
0

sin(x
3
)
sin(x
3
)
x
2
dydx = 2

1/3
0
sin(x
3
)x
2
dx
We have now an integral, which we can solve by substitu-
tion
=
2
3
cos(x
3
)[

1/3
0
=
4
3
Example: Integrate f(x, y) = y
2
over the region bound
by the x-axes, the lines y = x + 1 and y = 1 x. The
problem is best solved as a type I integral. As you can see
from the picture, we would have to compute 2 dierent
integrals as a type I integral. To do so, we have to write
the bounds as a function of y: they are x = y 1 and
x = 1 y

1
0

1y
y1
y
3
dx dy = 2

1
0
y
3
(1y) dy = 2(1/41/3) = 1/10 .
8
Example: Let R be the triangle 1 x 0, 0 y x.
What is
R
e
x
2
dxdy ?
The type I integral

1
0
[

1
y
e
x
2
dx]dy can not be solved
because e
x
2
has no anti-derivative in terms of elementary
functions.
The type II integral

1
0
[

x
0
e
x
2
dy] dx however can be
solved:
=

1
0
xe
x
2
dx =
e
x
2
2
[
1
0
=
(1 e
1
)
2
= 0.316... .
Example: The area of a disc of radius R is

R
R

R
2
x
2

R
2
x
2
1 dydx =

R
R

R
2
x
2
dx .
This integral can be solved with the substitution x =
Rsin(u), dx = Rcos(u)

/2
/2

R
2
R
2
sin
2
(u)Rcos(u) du =

/2
/2
R
2
cos
2
(u) du
Now continue with a trigonometc identity to get
R
2

/2
/2
(1+cos(2u)
2
du = R
2
. This is too complicated. We
will see how to do that better in polar coordinates.
Section 4.4: Polar coordinates and surface area
A polar region is bound by a curve given in polar coordinates as the curve (r(t), (t)). In carte-
sian coordinates the parametrization is r(t) = r(t) cos((t), r(t) sin((t). We are especially
interested in regions which are bound by polar graphs, where (t) = t.
Example: The polar graph dened by r() = cos(3) belongs to the class of roses r(t) =
[ cos(nt)[. Regions enclosed by this graph are also called rhododenea.
Example. The polar curve r() = 1 +sin() is called a cardioid. It looks like a heart. It is a
special case of limacon curves r() = 1 + b sin(). We call the inside of the region a limacon
region.
1.0 0.5 0.5 1.0
0.5
1.0
1.5
2.0
Integration in polar coordinates is
9

R
f(x, y) dxdy =

R
f(r cos(), r sin()r drd
Example: If
f(x, y) = x
2
+ x
2
+ xy ,
then
f(r cos(), r sin()) = r
2
+ r
2
cos() sin() .
Example: We have earlier computed area of the disc x
2
+ y
2
1 using substitution. It is
more elegant to do this integral in polar coordinates:

2
0

1
0
r drd = 2r
2
/2[
1
0
= .
Why do we have to include the factor r, when we move to polar coordinates? The reason is
that a small rectangle R with dimensions ddr in the (r, ) plane is mapped by
T : (r, ) (r cos(), r sin())
to a sector segment S in the (x, y) plane. It has approximately the area r ddr.
We can now integrate over type I or type II regions in the (, r) plane. like owers: (, r) [0
r f() where f() is a periodic function of .
A region R r coordinates is a type I
region
The same region in the xy coordinate
system is not type I or II.
10
Example: Integrate the function f(x, y) = 1 (, r()) [ r() [ cos(3)[ .

R
1 dxdy =

2
0

cos(3)
0
r dr d =

2
0
cos(3)
2
2
d = /2
Example: Integrate f(x, y) = y

x
2
+ y
2
over the region R = (x, y) [ 1 < x
2
+y
2
< 4, y > 0 .
Solution.

2
1

0
r sin()r r ddr =

2
1
r
3

0
sin() ddr =
(2
4
1
4
)
4

0
sin() d = 15/2
For integration problems, where the region is part of an annular region, or if you see function
with terms x
2
+ y
2
try to use polar coordinates x = r cos(), y = r sin().
Example: The Belgian Biologist Johan Gielis came up in 1997 with the family of curves
given in polar coordinates as
r() = (
[ cos(
m
4
)[
n1
a
+
[ sin(
m
4
)[
n2
b
)
1/n3
It is called the super-curve, because it can produce a variety of shapes like circles, square,
triangle, stars. It can also be used to produce super-shapes (see later).
The super-curve generalizes the super-ellipse which had been discussed in 1818 by Lame and
helps to tackle one of the more intractable problems in biology: describing form. A twist: Gielis
has patented his discovery!
11
A surface r(u, v) parametrized on a parameter domain R has the surface area

R
[r
u
(u, v) r
v
(u, v)[ dudv .
Note that r
u
is tangent to the grid curve u r(u, v) and r
v
is tangent to v r(u, v), the
two vectors span a parallelogram with area [r
u
r
v
[. A small rectangle [u, u +du] [v, v +dv]
is mapped by r to a parallelogram spanned by [r, r + r
u
] and [r, r + r
v
] which has the area
[r
u
(u, v) r
v
(u, v)[ dudv.
Example: consider the parametrized surface r(u, v) = 2u, 3v, 0. This surface is part of the
xy-plane. The parameter region G just gets stretched by a factor 2 in the x coordinate and by
a factor 3 in the y coordinate. r
u
r
v
= 0, 0, 6 and we see for example that the area of r(G)
is 6 times the area of G.
Example: The map r(u, v) = Lcos(u) sin(v), Lsin(u) sin(v), Lcos(v) maps the rectangle
G = [0, 2] [0, ] onto the sphere of radius L. We compute r
u
r
v
= Lsin(v)r(u, v). So,
[r
u
r
v
[ = L
2
[ sin(v)[ and

R
1 dS =

2
0

0
L
2
sin(v) dvdu = 4L
2
.
Example: For graphs (u, v) u, v, f(u, v), we have r
u
= (1, 0, f
u
(u, v)) and r
v
= (0, 1, f
v
(u, v)).
The cross product r
u
r
v
= (f
u
, f
v
, 1) has the length

1 + f
2
u
+ f
2
v
. The area of the surface
above a region G is

G

1 + f
2
u
+ f
2
v
dudv.
Example: Lets take a surface of revolution r(u, v) = v, f(v) cos(u), f(v) sin(u) on R =
[0, 2] [a, b]. We have r
u
= (0, f(v) sin(u), f(v) cos(u)), r
v
= (1, f

(v) cos(u), f

(v) sin(u))
and r
u
r
v
= (f(v)f

(v), f(v) cos(u), f(v) sin(u)) = f(v)(f

(v), cos(u), sin(u)). The surface

area is

[r
u
r
v
[ dudv = 2

b
a
[f(v)[

1 + f

(v)
2
dv.
12