Lab 9
Lab 9
Uploaded by
Adil Khan LodhiCopyright:
Available Formats
Lab 9
Lab 9
Uploaded by
Adil Khan LodhiCopyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Copyright:
Available Formats
Lab 9
Lab 9
Uploaded by
Adil Khan LodhiCopyright:
Available Formats
Signals & Systems Lab 9
35
-Department of Electronic Engineering-
9. Correlation:
Correlation function of the two sequences is the same as the convolution without the reversal of
one of the sequences. It may therefore be described as the integral of the product of two
sequences with one shifted relative to the other. The correlation function is used as a measure
of how well two sequences are correlated, or agree with one another, or are like one another.
9.1. Mathematical Form:
The Correlation function of the two sequences x
k
and y
k
is obtained by
This function may be extended to wave forms of infinite duration by writing them as
9.2. Cross-correlation:
Cross correlation is a measure of similarity between two waveforms as a function of time gap or
delay applied to one of them. The cross correlation between a pair of discrete time signals f(t)
and g(t) is given by
The index k is the shift parameter for discrete time signal. The order of subscripts 'fg' indicates
that f(n) is the reference sequence in that remains unshifted in time whereas the sequence g(n)
is shifted 'k' units in time with respect to f(n).
9.3. Auto-correlation:
Auto correlation of a discrete time signal is the correlation of the signal with itself. The auto
correlation of a discrete time signal f(n) it is defined as
Signals & Systems Lab 9
36
-Department of Electronic Engineering-
Or, equivalently we can write
9.4. Relation to Signal energy and Signal power:
The auto-correlation function of a periodic signal is itself a periodic signal with a period same as
that of the original signal. If f(n) is an energy signal, its auto-correlation is
After applying a zero shift it becomes the total signal energy of the signal as shown below:
If f[n] is a power signal, the auto-correlation at zero shift is the average signal power of the
signal as shown below:
Signals & Systems Lab 9
37
-Department of Electronic Engineering-
EXERCISES:
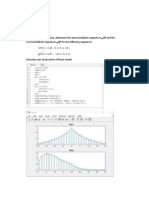
Task #1: Compute by hand, the complete autocorrelation function of following signal:
0 0 0 1 0 2 1 1
k
x
Task #2: Use xcorr command to compute the autocorrelation function of the sequence given in
Task 1.
Task #3: Calculate the energy of the given sequence in Task 1. Compare the result with its
autocorrelation function at n=0.
Task #4: Compute the cross correlation function r
xy
(n) of the given sequences below, for n = 0
through 4
0 1 0 0 2 0 1 0 0
k
x
0 0 0 0 6 . 0 8 . 0 1 0 0
k
y
Task #5: Write a script file which would calculate the autocorrelation of the data sequence of
task 1 without using the xcorr command of MATLAB.
You might also like
- Convolution and Correlation: ObjectivesDocument7 pagesConvolution and Correlation: ObjectivesAldon JimenezNo ratings yet
- NMK31003 DSP Lab 2 Module For Sem 2 2023 - 24Document9 pagesNMK31003 DSP Lab 2 Module For Sem 2 2023 - 24kajojim206No ratings yet
- Practice 7Document8 pagesPractice 7Jose Luis Arellano CamachoNo ratings yet
- Correlation and ConvolutionDocument15 pagesCorrelation and Convolutionতাহমিম হোসেন তূর্যNo ratings yet
- Lab # 2: Basic Operations On Discrete-Time: SequencesDocument9 pagesLab # 2: Basic Operations On Discrete-Time: SequencesIbad Ali KhanNo ratings yet
- ConvolutionDocument66 pagesConvolutionRavi Matthews100% (1)
- Experiments1 5Document15 pagesExperiments1 5Sameer ShaikhNo ratings yet
- Cs2403 - Digital Signal Processing Unit-I Signals & SystemsDocument18 pagesCs2403 - Digital Signal Processing Unit-I Signals & SystemsSuresh DskNo ratings yet
- DSP Lab ReportDocument22 pagesDSP Lab ReportMd AshikNo ratings yet
- EXPERIMENT2Document7 pagesEXPERIMENT2Sanjith PranavNo ratings yet
- National University of Modern Languages, Islamabad Communication System LabDocument7 pagesNational University of Modern Languages, Islamabad Communication System LabImMalikNo ratings yet
- Near Field Coupling With Small RFID ObjectsDocument5 pagesNear Field Coupling With Small RFID ObjectsDuc DucNo ratings yet
- Lab Manual # 04 Linear Convolution Objective: Description:: College of Electrical & Mechanical Engineering, NUSTDocument6 pagesLab Manual # 04 Linear Convolution Objective: Description:: College of Electrical & Mechanical Engineering, NUSTAhsanNo ratings yet
- Hybrid Control of Load Simulator For Unmanned Aerial Vehicle Based On Wavelet NetworksDocument5 pagesHybrid Control of Load Simulator For Unmanned Aerial Vehicle Based On Wavelet NetworksPhuc Pham XuanNo ratings yet
- FinalDocument78 pagesFinalsameera0627No ratings yet
- module IIDocument3 pagesmodule IIDaniel GetachewNo ratings yet
- Logistic Map Circuit PDFDocument8 pagesLogistic Map Circuit PDFmenguemengueNo ratings yet
- Journal 11Document6 pagesJournal 11Eccker RekcceNo ratings yet
- DSP Lab 3Document3 pagesDSP Lab 3Hafiz MuhammadNo ratings yet
- Homework 6Document10 pagesHomework 6manojreddyNo ratings yet
- John Arnold SamsonDocument5 pagesJohn Arnold SamsonJ Arnold SamsonNo ratings yet
- Active Learning Exercise #1 The LS Optimal Filter: The System Identification ProblemDocument3 pagesActive Learning Exercise #1 The LS Optimal Filter: The System Identification ProblemkleephNo ratings yet
- Big O Notation For Time Complexity of AlgorithmsDocument6 pagesBig O Notation For Time Complexity of AlgorithmsfreemhNo ratings yet
- Project 1 Matched Filters: Applications of Cross-CorrelationDocument4 pagesProject 1 Matched Filters: Applications of Cross-CorrelationDavidRubeomNo ratings yet
- Digital Signal Processing: B.E Ece (5Th Semester)Document17 pagesDigital Signal Processing: B.E Ece (5Th Semester)Saatwat CoolNo ratings yet
- 2 Discrete-Time Signals and Discrete-Time SystemsDocument29 pages2 Discrete-Time Signals and Discrete-Time SystemsVeena Divya KrishnappaNo ratings yet
- BEC505 - Digital Signal Processing - NOTESDocument102 pagesBEC505 - Digital Signal Processing - NOTESamritahelpworxNo ratings yet
- Harmonics NewDocument6 pagesHarmonics Newlvndr_snghNo ratings yet
- Application of MATLAB "Network Characteristic and Frequency Response"Document7 pagesApplication of MATLAB "Network Characteristic and Frequency Response"momen ShaheenNo ratings yet
- Automated Classification of Power Quality Disturbances Using SVM and RBF NetworksDocument7 pagesAutomated Classification of Power Quality Disturbances Using SVM and RBF NetworksbajricaNo ratings yet
- UNIT-8 Forms of Parallelism: 8.1 Simple Parallel Computation: Example 1: Numerical Integration Over Two VariablesDocument12 pagesUNIT-8 Forms of Parallelism: 8.1 Simple Parallel Computation: Example 1: Numerical Integration Over Two VariablesArshad ShaikNo ratings yet
- Digital Signal Processing (DSP)Document0 pagesDigital Signal Processing (DSP)www.bhawesh.com.npNo ratings yet
- Converging Algorithm For Calculation of Elements Current That Include Effects of Mutual CouplingDocument11 pagesConverging Algorithm For Calculation of Elements Current That Include Effects of Mutual Couplingwww.irjes.comNo ratings yet
- An Efficient Nonlinear Shift-Invariant Transformation - PsDocument8 pagesAn Efficient Nonlinear Shift-Invariant Transformation - PsΟλυμπίδης ΙωάννηςNo ratings yet
- The Genetic Algorithm For A Signal EnhancementDocument5 pagesThe Genetic Algorithm For A Signal EnhancementCarlyleEnergyNo ratings yet
- II. Combinational Logic Network (CLN) : 2.1 Definition and ClassificationDocument12 pagesII. Combinational Logic Network (CLN) : 2.1 Definition and ClassificationRyso SorinNo ratings yet
- Dsip Lab Manual Latest UpdatedDocument39 pagesDsip Lab Manual Latest Updatedmanas dhumalNo ratings yet
- Управление шунтирующим активным силовым фильтром с использованием адаптивных алгоритмов NLMS и QR-RLSDocument7 pagesУправление шунтирующим активным силовым фильтром с использованием адаптивных алгоритмов NLMS и QR-RLSRoma PervenenokNo ratings yet
- Klqgceb Ewvhja SCDocument8 pagesKlqgceb Ewvhja SCAbhishek PaloNo ratings yet
- Wavelets and Image Compression: Vlad Balan, Cosmin Condea January 30, 2003Document20 pagesWavelets and Image Compression: Vlad Balan, Cosmin Condea January 30, 2003Ashish PandeyNo ratings yet
- SNS Practical FinalDocument27 pagesSNS Practical FinalNishi VishwakarmaNo ratings yet
- Chapter 3Document50 pagesChapter 3Moon LilNo ratings yet
- Simulation of Series Active Filter For Unbalanced Loads: Greatkalai - Sasi@yahoo - Co.inDocument6 pagesSimulation of Series Active Filter For Unbalanced Loads: Greatkalai - Sasi@yahoo - Co.inphuongnhooNo ratings yet
- Digital Signal Processing Department of Electrical Engineering GCU LahoreDocument9 pagesDigital Signal Processing Department of Electrical Engineering GCU LahoreAhad AliNo ratings yet
- Experimnt 4Document2 pagesExperimnt 4amant6796No ratings yet
- Seismic MultiatributDocument18 pagesSeismic MultiatributLINDA ARDITA PUTRINo ratings yet
- A Matlab-Based Tool For Power System Dynamics Analysis: A Comparison With PSS/EDocument5 pagesA Matlab-Based Tool For Power System Dynamics Analysis: A Comparison With PSS/ELuis Alonso Aguirre LopezNo ratings yet
- cs2403 16marksDocument120 pagescs2403 16marksAnna PhilipsNo ratings yet
- A Machine Checked Proof That Ackermann's Function Is Not Primitive RecursiveDocument23 pagesA Machine Checked Proof That Ackermann's Function Is Not Primitive RecursiveTony ZhangNo ratings yet
- NewDocument7 pagesNewArjun VenkateshNo ratings yet
- Neural NetworksDocument37 pagesNeural NetworksOmiarNo ratings yet
- Code ReviewDocument5 pagesCode ReviewbaremuarNo ratings yet
- Department of Electrical Engineering Communication Systems: LAB-2 Convolution, Correlation, Energy and Power of SignalsDocument8 pagesDepartment of Electrical Engineering Communication Systems: LAB-2 Convolution, Correlation, Energy and Power of SignalsHamid AliNo ratings yet
- QM Hand in ProblemDocument3 pagesQM Hand in ProblemTobias DahlbergNo ratings yet
- Lab 05Document3 pagesLab 05Misbah Sajid ChaudhryNo ratings yet
- Diagrammatic Derivation of Gradient Algorithms For Neural NetworksDocument23 pagesDiagrammatic Derivation of Gradient Algorithms For Neural NetworksjoseNo ratings yet
- Mathematical Expectation: Lecture # 2Document17 pagesMathematical Expectation: Lecture # 2Adil Khan LodhiNo ratings yet
- The Following Transactions Are For The Accounts of HDocument9 pagesThe Following Transactions Are For The Accounts of HAdil Khan LodhiNo ratings yet
- Sampling DistributionDocument20 pagesSampling DistributionAdil Khan LodhiNo ratings yet
- Distributor Presentation: International Aeradio Pakistan (PVT) LTDDocument18 pagesDistributor Presentation: International Aeradio Pakistan (PVT) LTDAdil Khan LodhiNo ratings yet
- Summary of Chapter "Random Variable"Document10 pagesSummary of Chapter "Random Variable"Adil Khan LodhiNo ratings yet
- Ecu Worldwide (PVT) LTD.: Sindh Sales Tax InvoiceDocument1 pageEcu Worldwide (PVT) LTD.: Sindh Sales Tax InvoiceAdil Khan LodhiNo ratings yet
- Discrete Probability DistributionDocument12 pagesDiscrete Probability DistributionAdil Khan LodhiNo ratings yet
- Principles of Marketing: Consumer Markets and Consumer Buying BehaviorDocument35 pagesPrinciples of Marketing: Consumer Markets and Consumer Buying BehaviorAdil Khan LodhiNo ratings yet
- Assignment Journal and LedgersDocument5 pagesAssignment Journal and LedgersAdil Khan LodhiNo ratings yet
- Business Markets and Business Buyer BehaviorDocument11 pagesBusiness Markets and Business Buyer BehaviorAdil Khan LodhiNo ratings yet
- Trial Balance AssignmentDocument4 pagesTrial Balance AssignmentAdil Khan LodhiNo ratings yet
- MemberDocument77 pagesMemberAdil Khan LodhiNo ratings yet
- Bank Reconciliation Statements: Advanced LevelDocument5 pagesBank Reconciliation Statements: Advanced LevelAdil Khan LodhiNo ratings yet
- Income StatementDocument21 pagesIncome StatementAdil Khan LodhiNo ratings yet
- Depreciation AssignmentDocument2 pagesDepreciation AssignmentAdil Khan LodhiNo ratings yet
- WMT700 Datasheet B210917EN JDocument3 pagesWMT700 Datasheet B210917EN JAdil Khan LodhiNo ratings yet
- 24 Satmagan135-DatasheetDocument2 pages24 Satmagan135-DatasheetAdil Khan Lodhi100% (1)
- DSP Practice Problem 1 - SolutionDocument4 pagesDSP Practice Problem 1 - SolutionAdil Khan LodhiNo ratings yet
- PTU300 User's Guide in English M210796ENDocument221 pagesPTU300 User's Guide in English M210796ENAdil Khan LodhiNo ratings yet
- Articulated Coordinates: Page 1 of 4Document4 pagesArticulated Coordinates: Page 1 of 4Adil Khan LodhiNo ratings yet
- Bank Deposit Slip of Askari BankDocument1 pageBank Deposit Slip of Askari BankAdil Khan LodhiNo ratings yet
- Math QuestionsDocument2 pagesMath QuestionsManikyarajuNo ratings yet
- SEC4 FinalSlidesDocument90 pagesSEC4 FinalSlidesSandra BravoNo ratings yet
- Chapter - 12 ThermodynamicsDocument23 pagesChapter - 12 ThermodynamicsTilahun ArfichoNo ratings yet
- 08 - SQL Olap DB2Document45 pages08 - SQL Olap DB2Zahra NadineNo ratings yet
- Computer Science and Engineering: Syllabus of Undergraduate Degree Course B.Tech. V SemesterDocument32 pagesComputer Science and Engineering: Syllabus of Undergraduate Degree Course B.Tech. V SemesterabsdNo ratings yet
- Figure 1: Block Diagram of Gain Scheduling Adaptive Control Using DC ServomotorDocument5 pagesFigure 1: Block Diagram of Gain Scheduling Adaptive Control Using DC ServomotorafqzfieNo ratings yet
- Math 237 PreFinals Set ADocument1 pageMath 237 PreFinals Set AShunsui SyNo ratings yet
- Strassen AlgorithmDocument2 pagesStrassen AlgorithmNilayan AhmedNo ratings yet
- CS 2032 - Data Warehousing and Data Mining PDFDocument3 pagesCS 2032 - Data Warehousing and Data Mining PDFvelkarthi92No ratings yet
- 5330-Article Text-8555-1-10-20200508Document8 pages5330-Article Text-8555-1-10-20200508fbao9275No ratings yet
- GPU Architecture and Parallel Programming: Tiled Convolution AnalysisDocument18 pagesGPU Architecture and Parallel Programming: Tiled Convolution AnalysisAndy OrtizNo ratings yet
- Underlying AssumptionDocument2 pagesUnderlying AssumptionBharat SharmaNo ratings yet
- Error Detection and Correction in Data Link LayerDocument16 pagesError Detection and Correction in Data Link LayerAlexander PhiriNo ratings yet
- Regression: 9.1.1 DefinitionDocument20 pagesRegression: 9.1.1 DefinitionBhawna JoshiNo ratings yet
- Huffman Coding, RLE, LZWDocument41 pagesHuffman Coding, RLE, LZWamandaNo ratings yet
- Linear Programming Example 1992 UG ExamDocument6 pagesLinear Programming Example 1992 UG ExamDhyz QuinquilleriaNo ratings yet
- Curve Fitting ST Line and ParabolaDocument12 pagesCurve Fitting ST Line and ParabolaRakesh K0% (1)
- Lampiran Uji Regresi Linear BergandaDocument3 pagesLampiran Uji Regresi Linear Bergandakhrisna02No ratings yet
- Transportation AlgorithmDocument41 pagesTransportation AlgorithmBinyam Kebede100% (1)
- Cos2601 2022 0 104Document5 pagesCos2601 2022 0 104SnowNo ratings yet
- Course: Artificial Intelligence Instructor: Naveed Kazim Khan Federal Urdu University of Arts, Science and Technology, IslamabadDocument22 pagesCourse: Artificial Intelligence Instructor: Naveed Kazim Khan Federal Urdu University of Arts, Science and Technology, IslamabadRana HafeezNo ratings yet
- Metode KrigingDocument11 pagesMetode Krigingshabila gadisNo ratings yet
- Gilbert-Johnson-Keerthi Distance Algorithm: Convex Sets Support Function Simplices Minkowski DifferenceDocument2 pagesGilbert-Johnson-Keerthi Distance Algorithm: Convex Sets Support Function Simplices Minkowski DifferenceWilfredo Jara TiconaNo ratings yet
- Impact Factor ListDocument216 pagesImpact Factor ListSurya DilaNo ratings yet
- Wha1.3, Mom Bailey DewsnapDocument21 pagesWha1.3, Mom Bailey DewsnapBailey DewsnapNo ratings yet
- Class Ix - Artificial Intelligence - Unit-2 Ai Project Cycle Assignment-1Document4 pagesClass Ix - Artificial Intelligence - Unit-2 Ai Project Cycle Assignment-1Kiran Raghav0% (2)
- AI 900 DemoDocument9 pagesAI 900 Demohasnaouiriadh047No ratings yet
- Performance Task For WLP OutputDocument1 pagePerformance Task For WLP OutputFernandoGavinCautonNo ratings yet
- Monkey and BananaDocument22 pagesMonkey and Bananatrupti.kodinariya981050% (2)
- A Comparative Study On Market Basket Analysis and Apriori Association TechniqueDocument4 pagesA Comparative Study On Market Basket Analysis and Apriori Association TechniqueRofi Abul HasaniNo ratings yet