0 ratings0% found this document useful (0 votes)
73 viewsProblem Set - Finals
Problem Set - Finals
Uploaded by
Jason TylerThis document contains 12 multi-part physics problems involving concepts like kinematics, energy, momentum, rotational motion, and statics. The problems cover scenarios like particles sliding on inclined planes and tracks, blocks connected by springs and strings over pulleys, rolling spheres, collisions between bullets and blocks, and a beam with a bear walking out to retrieve food. Learners are asked to determine values like speeds, distances, energies, forces, and coefficients of friction by applying equations related to these fundamental physics concepts.
Copyright:
© All Rights Reserved
Available Formats
Download as DOCX, PDF, TXT or read online from Scribd
Problem Set - Finals
Problem Set - Finals
Uploaded by
Jason Tyler0 ratings0% found this document useful (0 votes)
73 views3 pagesThis document contains 12 multi-part physics problems involving concepts like kinematics, energy, momentum, rotational motion, and statics. The problems cover scenarios like particles sliding on inclined planes and tracks, blocks connected by springs and strings over pulleys, rolling spheres, collisions between bullets and blocks, and a beam with a bear walking out to retrieve food. Learners are asked to determine values like speeds, distances, energies, forces, and coefficients of friction by applying equations related to these fundamental physics concepts.
Original Description:
Physics
Copyright
© © All Rights Reserved
Available Formats
DOCX, PDF, TXT or read online from Scribd
Share this document
Did you find this document useful?
Is this content inappropriate?
This document contains 12 multi-part physics problems involving concepts like kinematics, energy, momentum, rotational motion, and statics. The problems cover scenarios like particles sliding on inclined planes and tracks, blocks connected by springs and strings over pulleys, rolling spheres, collisions between bullets and blocks, and a beam with a bear walking out to retrieve food. Learners are asked to determine values like speeds, distances, energies, forces, and coefficients of friction by applying equations related to these fundamental physics concepts.
Copyright:
© All Rights Reserved
Available Formats
Download as DOCX, PDF, TXT or read online from Scribd
Download as docx, pdf, or txt
0 ratings0% found this document useful (0 votes)
73 views3 pagesProblem Set - Finals
Problem Set - Finals
Uploaded by
Jason TylerThis document contains 12 multi-part physics problems involving concepts like kinematics, energy, momentum, rotational motion, and statics. The problems cover scenarios like particles sliding on inclined planes and tracks, blocks connected by springs and strings over pulleys, rolling spheres, collisions between bullets and blocks, and a beam with a bear walking out to retrieve food. Learners are asked to determine values like speeds, distances, energies, forces, and coefficients of friction by applying equations related to these fundamental physics concepts.
Copyright:
© All Rights Reserved
Available Formats
Download as DOCX, PDF, TXT or read online from Scribd
Download as docx, pdf, or txt
You are on page 1of 3
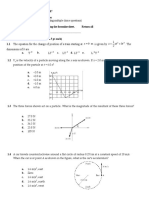
PROBLEM SET - FINALS
1. A particle of mass m = 5 kg is released
from point A and slides on a frictionless track
shown in the figure. Determine the particles
speed at points B and C.
2. Two objects are connected by a light string passing over a
light, frictionless pulley as shown. The object of mass 5 kg is
released from rest. Using energy method, (a) determine the
speed of the 3 kg object just as the 5 kg object hits the
ground. (b) Find the maximum height to which the 3 kg
object rises.
3. A 5 kg block is set into motion up the inclined plane with
an initial speed of 8 m/s. The block comes to rest after
traveling 3 m along the plane which is inclined at 30 o to the
horizontal. For this motion, determine the blocks (a) change
in kinetic energy, (b) change gravitational potential energy.
(c) What is the frictional force exerted on the block and (d)
the coefficient of kinetic friction?
4. A 10 kg block is released from point A. The track is frictionless except for the
portion between points B and C which has a
length of 6 m. The block travels down the
track, hits a spring of force constant k = 2
250 N/m, and compresses the spring 0.30 m
from its equilibrium position before coming to
rest momentarily. Determine the coefficient of
kinetic friction between the block and the rough surface between B and C.
5. A block of mass 5 kg is pushed against a horizontal spring of negligible mass until
the spring is compressed a distance x. the force
constant of the spring is 450 N/m. When it is
released, the block travels along a frictionless,
horizontal surface to point B, the bottom of the
vertical circular track of radius R = 1 m, and
continues to move along the track. The speed of the
block at the bottom is vB = 12 m/s, and the block
experiences an average friction force of 7 N while
sliding up the track. (a) What is x? (b) What speed
do you predict for the block at the top of the track? (c) Does the block actually reach
the top of the track, or does it fall off before reaching the top?
6. A pendulum, comprising a light string of length L and a small
sphere, swings in the vertical plane. The string hits a peg located a
distance d below the point of suspension. (a) Show that the sphere
is released from a height below that of the peg. (b) Show that if the
pendulum is released from the horizontal position ( = 90 o) and is
to swing in a complete circle centered on the peg, the minimum
value of d must be 3L/5.
7. Two blocks are free to slide along at the frictionless wooden track ABC as shown.
The block of mass m1 = 5 kg is released
from A. Protruding from its front end is the
north pole of a strong magnet, which is
repelling the north pole of an identical
magnet embedded in the back end of the
block of mass m2 = 10 kg, initially at rest.
The two blocks never touch. Calculate the
maximum height to which m1 rises after the elastic collision.
8. A particle of mass 1.18 kg is attached
between two identical springs on a
horizontal, frictionless tabletop. Both
springs have spring constant k and are
initially unstressed. (a) The particle is
pulled a distance x along a direction
perpendicular to the initial configuration
of the springs as shown. Show that the
force exerted on the particle is
(b) Show that the potential energy of the system is
(c) Assume L = 1.2 m, k = 40 N/m. If the particle is pulled 0.50 m to the right and
then released, what is its speed when it reaches the equilibrium point x = 0?
9. A bullet of mass m = 50 g is fired into a block of mass M = 0.750 kg which is
initially at rest at the edge of a frictionless table of height h = 80 cm. The bullet
remains in the block, and after impact the block lands
a distance d = 1.80 m from the bottom of the table.
Determine the speed of the bullet.
10. A 5 g bullet moving with
an initial speed of 400 m/s is
fired into and passes through
block, initially at rest on a
is connected to a spring with k
5 cm to the right after impact.
the bullet emerges from the
energy converted into internal
a 1 kg block as shown. The
frictionless, horizontal surface,
= 900 N/m. The block moves
Find (a) the speed at which
block and (b) the mechanical
energy in the collision.
11. A solid sphere of mass m and radius r rolls without
slipping along the track as shown. It starts from rest with
the lowest point of the sphere at height h above the
bottom of the loop of radius R much larger than r. (a) What
is the minimum value of h (in terms of R) such that the
sphere completes the loop? (b) What are the components
of the net force on the sphere at the point if h = 3R?
12. A hungry bear weighing 700 N walks out on a beam in an
attempt to retrieve a basket of food hanging at the end of
the beam. The beam is uniform, weighs 200 N, and is 6 m
long. The basket weighs 80 N. (a) Draw a free body diagram
for the beam. (b) When the bear is at x = 1 m, find the
tension in the wire and the component of the force exerted
by the wall on the left end of the beam. (c) What if the wire
can withstand a maximum tension of 900 N, what is the
maximum distance the bear can walk before the wire
breaks?
You might also like
- Physics Review PDFDocument27 pagesPhysics Review PDFRizahGepes100% (5)
- DJJ30093 Chapter 1 Dem 3Document17 pagesDJJ30093 Chapter 1 Dem 3Sushantan SubramanyamNo ratings yet
- PH600 CH 9 Problems PDFDocument3 pagesPH600 CH 9 Problems PDFMike GaoNo ratings yet
- Double Slit Interference LabDocument3 pagesDouble Slit Interference LabLabib Haque100% (1)
- Practice Sheet WPEDocument9 pagesPractice Sheet WPENaveen JaferNo ratings yet
- Work Power EnergyDocument9 pagesWork Power EnergySanmati Jain100% (1)
- Mechanics Good Questions 1.: Z Q P y P R X R QDocument4 pagesMechanics Good Questions 1.: Z Q P y P R X R QrajdeepNo ratings yet
- WORK POWER ENERGY - ASSIGNMENTyDocument3 pagesWORK POWER ENERGY - ASSIGNMENTysaiprittNo ratings yet
- 4.1.1a TestDocument31 pages4.1.1a TestutheinsweNo ratings yet
- WORK POWER ENERGY-05-Subjective UnSolvedDocument7 pagesWORK POWER ENERGY-05-Subjective UnSolvedRaju SinghNo ratings yet
- Part - I: Subjective Questions: Section (A) : Calculation of Centre of MassDocument14 pagesPart - I: Subjective Questions: Section (A) : Calculation of Centre of MassRaman GoyalNo ratings yet
- Tutorial 3Document4 pagesTutorial 3nas123456789No ratings yet
- Centre of Mass & Consv of Momentum (Nitin M Sir) PDFDocument5 pagesCentre of Mass & Consv of Momentum (Nitin M Sir) PDFkisan singhNo ratings yet
- Unit 4 ExercisesDocument4 pagesUnit 4 Exercises张书No ratings yet
- M1 Dynamics - Connected ParticlesDocument32 pagesM1 Dynamics - Connected ParticlesDarla FennNo ratings yet
- FR MomentumDocument22 pagesFR MomentumJanel Edwards0% (1)
- AssignmentDocument4 pagesAssignmentKhyzer HayyatNo ratings yet
- Sankalp - Phase Ii - Wep - 4 - 052300Document4 pagesSankalp - Phase Ii - Wep - 4 - 052300Dipesh SinglaNo ratings yet
- Physics 11Document12 pagesPhysics 11Jane100% (1)
- (Centre of Mass, Momentum & Collision) Exercise-IDocument4 pages(Centre of Mass, Momentum & Collision) Exercise-IAyush ChouhanNo ratings yet
- Com Sub Q PDFDocument4 pagesCom Sub Q PDFAyush ChouhanNo ratings yet
- Final Exam W07Document5 pagesFinal Exam W07Malik ANo ratings yet
- Work, Energy&Power (Nitin M Sir)Document6 pagesWork, Energy&Power (Nitin M Sir)Kenny RuizNo ratings yet
- Assignment 1 SolutionDocument10 pagesAssignment 1 SolutionTalha JabbarNo ratings yet
- Wa0010.Document3 pagesWa0010.BxkxnzixbNo ratings yet
- Phys1101 Worksheeti 2014 EDocument6 pagesPhys1101 Worksheeti 2014 Ejhxnrx48f8No ratings yet
- NL CQ 6 SSPDocument4 pagesNL CQ 6 SSPGokul NathNo ratings yet
- Centre of Mass & Consv of Momentum (Nitin M Sir)Document5 pagesCentre of Mass & Consv of Momentum (Nitin M Sir)Kenny Ruiz0% (1)
- Part - I: Subjective Questions: Section (A) : Calculation OF Centre of MassDocument26 pagesPart - I: Subjective Questions: Section (A) : Calculation OF Centre of MassBalaji Classes washimNo ratings yet
- PHY11 Problem SetDocument24 pagesPHY11 Problem SetAlyssa AtienzaNo ratings yet
- Physics 71 2nd LE ReviewerDocument3 pagesPhysics 71 2nd LE ReviewerAnne Glydel Cruzado DalaganNo ratings yet
- Ch8 Review Problems NewDocument6 pagesCh8 Review Problems NewVic VanceNo ratings yet
- Circular Motion and WPEDocument5 pagesCircular Motion and WPEMy Moto G2No ratings yet
- Problem Set2 PDFDocument1 pageProblem Set2 PDFMr. DummyNo ratings yet
- Center of Mass - 984a8dcc Ae61 441d Aebc 8cb60d6692c6Document31 pagesCenter of Mass - 984a8dcc Ae61 441d Aebc 8cb60d6692c6veereshgajwelNo ratings yet
- Lista 3Document4 pagesLista 3Thales FreireNo ratings yet
- WPEDocument6 pagesWPESanjeev KumarNo ratings yet
- AL 22 M1 Connected ParticlesDocument5 pagesAL 22 M1 Connected ParticlesSenuja ChammithaNo ratings yet
- Assignment - Momentum & CollisionDocument5 pagesAssignment - Momentum & CollisionKalpan ShahNo ratings yet
- All AnswersDocument22 pagesAll AnswersNadiatul JannahNo ratings yet
- Three Identical BallsDocument5 pagesThree Identical BallsharshanauocNo ratings yet
- Subjective Questions: Work, Power & EnergyDocument5 pagesSubjective Questions: Work, Power & EnergySamridh GuptaNo ratings yet
- WEP Narayana SheetsDocument6 pagesWEP Narayana Sheetsrahuljain1100% (1)
- Physics C FRQ PracticeDocument12 pagesPhysics C FRQ Practiceamelia_823No ratings yet
- Sheet Exercise 2 - WEP - S-2 1683019532469Document6 pagesSheet Exercise 2 - WEP - S-2 1683019532469SAHIL KUMAWATNo ratings yet
- m1 Dynamics Connected ParticlesDocument17 pagesm1 Dynamics Connected ParticlesAjmalMansoorNo ratings yet
- Ch3 - Section BDocument2 pagesCh3 - Section Bhemengebeyehu862No ratings yet
- Topic C: Energy - Examples SPRING 2014: V V V V e 0.0 e 0.5 e 1.0Document9 pagesTopic C: Energy - Examples SPRING 2014: V V V V e 0.0 e 0.5 e 1.0ettypasewangNo ratings yet
- Prob01s - H C VermaDocument6 pagesProb01s - H C VermaManoj KumarNo ratings yet
- Physics Rotational Dynamics PDFDocument11 pagesPhysics Rotational Dynamics PDFAshish RanjanNo ratings yet
- Assignment AwetalDocument19 pagesAssignment AwetalTapendra BistNo ratings yet
- Wiley Part2Document9 pagesWiley Part2Andrian Dean Handika CsTahtaNo ratings yet
- Practice Test2 ps150Document3 pagesPractice Test2 ps150Antoine S. NdiayeNo ratings yet
- PhysicsDocument3 pagesPhysicsmickey_disney93No ratings yet
- Conservation of Linear MomentumDocument15 pagesConservation of Linear MomentumSiddharth Acharya100% (1)
- SwerdwsDocument4 pagesSwerdwsTú ĐoànNo ratings yet
- Physics Midterm 2 QuestionsDocument2 pagesPhysics Midterm 2 QuestionsapaikshoppingNo ratings yet
- Explain Quantum Physics With a Single-Particle in Motion: Anharmonic OscillatorFrom EverandExplain Quantum Physics With a Single-Particle in Motion: Anharmonic OscillatorNo ratings yet
- O level Physics Questions And Answer Practice Papers 2From EverandO level Physics Questions And Answer Practice Papers 2Rating: 5 out of 5 stars5/5 (1)
- Me 22015 CH17Document18 pagesMe 22015 CH17RyanNo ratings yet
- SAT Subject Physics Formula ReferenceDocument14 pagesSAT Subject Physics Formula Referencementalist302No ratings yet
- Bridge Failures & DisastersDocument17 pagesBridge Failures & DisasterseliasjamhourNo ratings yet
- Flight Stability of An Asymmetric Projectile With Activating CanardsDocument8 pagesFlight Stability of An Asymmetric Projectile With Activating Canardsali_raza117No ratings yet
- Lecture-4 - Rotational Motion & Work EnergyDocument17 pagesLecture-4 - Rotational Motion & Work EnergyEmran HosenNo ratings yet
- Engineering Mechanics Course Description and ContentsDocument2 pagesEngineering Mechanics Course Description and ContentsSarah LeonenNo ratings yet
- Bernoulli's PrincipleDocument17 pagesBernoulli's Principletemp111tempNo ratings yet
- Trigonometric Functions of Acute AnglesDocument16 pagesTrigonometric Functions of Acute Anglesbyunbacooon456No ratings yet
- Flow Past A Rotating CylinderDocument33 pagesFlow Past A Rotating CylinderBình Lê ĐứcNo ratings yet
- Experiment 3 Law of Conservation of EnergyDocument9 pagesExperiment 3 Law of Conservation of EnergyHafiz MuhammadNo ratings yet
- 02 Microwave Experiment Manual - PolarizationDocument2 pages02 Microwave Experiment Manual - PolarizationAriel Carlos CaneteNo ratings yet
- Thesis QuadrotorDocument4 pagesThesis Quadrotorsamantharandallomaha100% (2)
- Tutorial 5Document13 pagesTutorial 5clarence limNo ratings yet
- Prelimsk 93%Document13 pagesPrelimsk 93%jrenceNo ratings yet
- Propagation of Radio Waves in The AtmosphereDocument14 pagesPropagation of Radio Waves in The AtmosphereJuampi MochenNo ratings yet
- US20060071122A1 - Full Body Teleportation System - Google PatentsDocument1 pageUS20060071122A1 - Full Body Teleportation System - Google PatentsGinnNo ratings yet
- Stationary Waves Exam Q and ADocument20 pagesStationary Waves Exam Q and AVanessa AdetuNo ratings yet
- HydraulicsDocument5 pagesHydraulicsbakrichodNo ratings yet
- Bartolome Clarisse E BSCE 1B Activity 2 Excel Functions and ChartDocument4 pagesBartolome Clarisse E BSCE 1B Activity 2 Excel Functions and ChartCyrus De LeonNo ratings yet
- Dynamic Lab 2 Physical PendulumDocument24 pagesDynamic Lab 2 Physical Pendulumadib haikalNo ratings yet
- Handbook NewDocument26 pagesHandbook NewthamarairrrNo ratings yet
- The Physics of Ski Jumping, NotesDocument9 pagesThe Physics of Ski Jumping, NotesdavparanNo ratings yet
- Unit - IVDocument56 pagesUnit - IVharikaranNo ratings yet
- Prob 06.71Document2 pagesProb 06.71Venkat DalaiNo ratings yet
- Mahalingam 1957Document5 pagesMahalingam 1957Oussama AkrmiNo ratings yet
- Projectile Motion (Theory)Document5 pagesProjectile Motion (Theory)Mohammed Aftab Ahmed100% (1)
- Experiment # 4: Moment of Inertia of Flywheel When Subjected To Different Loads ObjectiveDocument3 pagesExperiment # 4: Moment of Inertia of Flywheel When Subjected To Different Loads Objectiveharis shahNo ratings yet