ECEG 351 Electronics II Spring 2019

ECEG 351 Electronics II Spring 2019
Homework Assignment #7 – due in BRKI 368 at 5:00 pm on Friday, Apr. 5, 2019

[Prob. 8 postponed to HW #8]
Instructions, notes, and hints:
Provide the details of all solutions, including important intermediate steps. You will not receive
credit if you do not show your work. Some problems might be solvable (or must be solved) using
good engineering approximations or assumptions. In those cases, your answer might differ from
the posted answer by a fairly large margin. Given typical device variations and component
tolerances, that amount of discrepancy is often reasonable. If you justify any approximations you
make, you will be given full credit for such answers.
Assignment:
1. The diagram below is the small-signal model of the output port of a common-emitter
amplifier and its load. Show that the output voltage is given by the symbolic expression
shown next to the diagram. Briefly explain the significance of the frequency-dependent part
of the expression (the fraction to the right of RC||RL).
jω ( RC + RL ) Co
Co vo = − g m vbe ( RC RL )
0.01 µF 1 + jω ( RC + RL ) Co
gmvbe +
RC RL
100 kΩ vo
3.3 kΩ −
2. For the partial amplifier small-signal model considered in the previous problem, find the cut-
off frequency (in Hz) associated with capacitor Co. Then, assuming that vbe = vin, calculate
the magnitude of the midband voltage gain vo/vin and that of the voltage gain at the cut-off
frequency. Assume that the amplifier has a quiescent current of IC = 2.0 mA, the emission
coefficient is n = 1, and VT = 25 mV.
3. [adapted from Prob. 10.15 of Sedra & Smith, 7th ed.] Starting with the expression that gives
fT for a MOSFET and making the approximation that Cgs >> Cgd and that the overlap
component of Cgs is negligibly small, show that
gm 1.5 µn I D
fT = is approximated by fT ≈ .
2π ( Cgs + Cgd ) π L 2CoxWL
(See Sec. 10.2.1 in the textbook for a discussion of overlap capacitance.) This result implies
that operation at a high quiescent drain current value leads to a high fT. It also implies that
faster operation results from smaller devices.
(continued on next page)

4. [adapted from Prob. 10.45 of Sedra & Smith, 7th ed.] It is possible to determine the unity-
gain frequency of a BJT by making careful measurements of the equivalent impedance of the
device in the diode-connected configuration as shown below. (The required bias circuit is not
shown in the diagram.) Assuming that α = β/(β+1) ≈ 1, and using the BJT high-frequency
hybrid-π model with rx = 0 and ro = ∞,
a. Derive an expression for Zi(ω) as a function of ω, re, and Cπ (where re is given in

Table 7.3 of the textbook).
b. Show that the frequency at which the impedance Zi(ω) has a phase angle of ±45° is fT
if the quiescent collector current is high enough so that Cπ >> Cµ.
c. Show that if the quiescent collector current is reduced so that impedance Zi(ω) has a
phase angle of ±45° at the frequency 2fT, then Cπ ≈ Cµ.
5. Estimate the upper and lower limits of the midband range for the common-gate amplifier
circuit shown below. Before finding the numerical values of the pole frequencies, first find
symbolic expressions for the equivalent resistances seen by each capacitance in the circuit.
Note that you will need to find the quiescent drain current. The MOSFET has parameter
values kn = 4 mA/V2, Vt = 1 V, Cgs = 30 pF, Cgd = 2.0 pF; Cds is negligibly small, and ro is
large enough to ignore. Identify which single capacitors have the most dominant effect in
determining the upper and lower limits of the midband region.
Rsig Ci Co
50 Ω 10 µF 1 µF
vo
+ RD RL
−
RS RG1 2 kΩ 10 kΩ
vsig 2 kΩ 1 MΩ
CG
RG2 VDD = +12 V
3300 pF Cby
1 MΩ
10 µF
6. The upper limit fH of the midband range for the amplifier considered in the previous problem
is about 35 MHz. The value of fH can be reduced by adding a capacitance CL across the load
RL. Find the value of CL that would be necessary to reduce fH to approximately 3 MHz. The
parameter values and assumptions are unchanged from the previous problem.
(continued on next page)

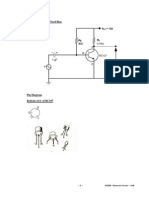
7. Estimate the values of Cπ and Cµ for the BJT in the circuit shown below. You will need to
obtain some information from the 2N3904 data sheet, which is available on the Laboratory
page at the course web site. The data sheet gives the unity-gain frequency fT for a collector
current of 10 mA; however, that value can be used with reasonable accuracy for the different
collector current in the circuit considered here. The variable Cobo is used in many data sheets
to represent Cµ in the hybrid-pi model. The value of Cµ is mostly unaffected by the quiescent
collector current.
VCC = 12 V
CCC
R1
130 kΩ
VCB +
Rsig = 50 Ω 2N3904
−
Ci Co = 0.5 µF
R2
+ 0.5 µF
− 39 kΩ
vsig +
RE vo RL
3.9 kΩ − 51 Ω
8. [Postponed to HW #8] The common emitter amplifier shown below uses the collector-to-
base feedback biasing method. With the component values shown, the quiescent collector
current is close to 500 µA, and the quiescent collector voltage is close to 6 V. Find the small-
signal midband voltage gain Av = vo/vin, and estimate the upper and lower frequency limits of
the midband range. If you need a value for β (you shouldn’t), you may assume that it is
approximately equal to 150. The datasheet for the 2N3904 is available on the Laboratory
page of the course web site.
VCC = 12 V
CCC = 10 µF
RC
11 kΩ Co = 0.5 µF
Ci R1 IC +
RL
Rsig = 100 Ω 2.2 µF 100 kΩ vo
100 kΩ
vin −
2N3904
+ R2
vsig − 15 kΩ

ECEG 351 Electronics II Spring 2019

Uploaded by

Copyright:

Available Formats

ECEG 351 Electronics II Spring 2019

Uploaded by

Document Information

Original Title

Copyright

Available Formats

Share this document

Share or Embed Document

Sharing Options

Did you find this document useful?

Is this content inappropriate?

Copyright:

Available Formats

ECEG 351 Electronics II Spring 2019

Uploaded by

Copyright:

Available Formats

ECEG 351 Electronics II Spring 2019

Homework Assignment #7 – due in BRKI 368 at 5:00 pm on Friday, Apr. 5, 2019

Instructions, notes, and hints:

(continued on next page)

a. Derive an expression for Zi(ω) as a function of ω, re, and Cπ (where re is given in

(continued on next page)

You might also like