Kinetics and Mechanisms of Inorganic Reactions in Solution

Hussain Ullah
Kinetics and mechanisms of inorganic reactions in solution
Hussain Ullah
Ph.D Scholar
DEPARTMENT OF CHEMISTRY
QUAID-I-AZAM UNIVERSITY
ISLAMABAD 45320
PAKISTAN
Never lose hope until it’s over, completely

Chap-1 1 Hussain Ullah
Kinetics and reaction mechanisms in inorganic chemistry

Despite extensive study, inorganic chemistry has yet to achieve the understanding of reaction
mechanisms enjoyed by organic chemistry; this situation can be attributed to the inherent
difficulties involved in trying to systematize the reactions of more than one hundred elements.
Even attempts to predict from one element to another in the same group are not always
successful.
Ideally, chemists hope to understand a number of reaction mechanisms well enough that
predictions about a diverse assortment of complexes involving different metals ligands, and
reaction conditions can be made. To understand the kinetics of reaction mechanism the
knowledge of kinetics terms is necessary.
Basic Terminology
As with most fields, the study of reaction kinetics has some terminology with which one must be
familiar in order to understand advanced books and research papers in the area. The following is
a summary of some of these basics terms and definitions. Many of these may be known from
previous studies in the introductory and physical chemistry and further background can be
obtained from text books devoted to the physical chemistry aspects of reaction kinetics.
Rate of a reaction:
The rate of change of concentration of reactants or products with time is called rate of reaction.
According to the reaction,
(With respect to reactants)
(With respect to products)
Rate Law:
The rate law is the experimentally dependence of the reaction rate on reagent concentrations. It
has the following general form. . Where order of reaction is m + n and k is
proportionality constant called the rate constant. The exponent m and n are determined
experimentally from the kinetic study and have no necessary relationship to the stoichiometric
coefficient in the balanced chemical reaction. The rate law may contain species that do not
appear in the balanced reaction and may be the sum of several terms for different reaction
pathways. The rate law is an essential piece of mechanistic information because it contains the

concentrations of species necessary to get from the reactant to the product by the lowest energy
pathway. A fundamental requirement of an acceptable mechanism is that it must predict a rate
law consistent with the experimental law.
Order of the rate law:
The order of the rate law is the sum of the exponents in the rate law. For example, if m = 1 and n
= -2, then according to the above equations, the rate law has an overall order of -1. However,
except in the simplest cases, it is best to describe the order with respect to individual reagents.
The order of a reaction is from –ive to +3.
Rate constant:
The rate constant, k, is the proportionality constant that relates the rate to the reagent
concentrations (or activities, or pressure, for example), as shown in the above equation. The units
of k depend on the rate law and must give the right-hand side of the above equation, the same
units as the left-hand side.
Half-time:
The half-time, t1/2, is the time required for a reactant concentration to change by half of its total
change. This term is used to convey a qualitative idea of the time scale for the reaction and has a
quantitative relationship to the rate constant in simple cases. In complex system, the half-time
may be different and one should specify the reagent to which the t1/2 refers.
Lifetime:The life, for particular specie is the concentration of that species divided by its rate of
disappearance. This term is commonly used in so-called lifetime method, such as NMR, and in
relaxation method, such as temperature jump.
Analysis of Rate Data
In general, a kinetic study begins with the collection of data of concentration versus time of a
reactant or product. As will be seen later, this can also be accompanied by determining the time
dependence of some variable that is proportional to concentration, such as absorbance or NMR
peak intensity. The next step is to fit the concentration-time data to some model that will allow
one to determine the rate constant if the data fits the model. For this some integrated rates law
must be encounter in inorganic kinetics.
So the main approach to the mechanism is the kinetic one, emphasis is placed on the rate
measurements and their interpretations (Benson).

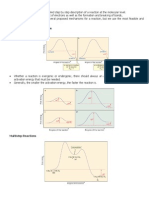
Theories of reaction rates

According to the theory of absolute reaction rates, the reactants in a chemical reaction are in
equilibrium with an energetic species known as the activated complex. The thermal energy
required to make such a complex is called the activation energy. The activated complex
occupies an energy level called the transition state which occurs at the point of higher energy
on the path from one stable configuration to another as in fig-1(Benson). The full rate law will
involve all species necessary to form the transition state. An intermediate is the species present at
any valley on a reaction coordinate diagram. When a valley is shallow, it can be ambiguous
whether or not an intermediate really is formed. In chemistry, an intermediate is expected to have
a lifetime longer than a few vibrational lifetimes (>10-3s) and the valley should be deeper than
the thermal energy (RT = 2.5kJ mol-1 at 25oC).
Figure 1 Reaction profile showing position of transition and intermediate state.

There are two paths of this diagram
1. Thermodynamic path.
Energy gap between reactant and product is concerned with thermodynamics. It deals with
stability of product and and possibility of reaction.
1. Kinetic path
Reaction gap between reactants and activated complex. Kinetics is supported by thermodynamics.
If a reaction is feasible than what is the rate of the reaction? Here in this course we will be
concerned with kinetics and not thermodynamics but thermodynamics act as a pioneer for
kinetics. If the height of the transition state is greater than activation energy will also be high. It

means the kinetics of the reaction is smaller (rate) and if the height of the energy profile diagram
is smaller the rate of reaction is high. So kinetics tell us about rate and factors affecting rate of a
reaction.
Rate of reaction on the basis of thermodynamic approach
Rate of reaction
Rate of reaction is defined as rate of change of reactants or products per unit time.
Mathematically it can be represented as,
Where x is small change in the concentration of reactants or products.

Let suppose a reaction given below as,
⇔ →M+N( is an activated complex)
(Rate of disappearance of reactants)
(Rate of appearance of product)
The above equations can be represented schematically as

M+N
Conc
A+B
Time
Keeping in view the kinetics of a reaction there are two types of reactions
1. Fast reactions: those reactions
AgNO3 + NaCl AgCl(s) + NaNO3
2. Slow reactions: Rusting of iron
3. Extremely slow reactions: decomposition of H2O
Quantitatively the rate of passage from one stable state to the next can be derived from a
thermodynamic approach.
Consider a simple reaction
A+B [X#] M+N
At equilibrium [X#] = K# [A][B] or [K#] =[X#]/[A][B] (1)

and we know that the rate of formation of product is
(2) Putting eq (1) in eq (2) eq (3)
as K2 = so eq (3) can be written as (4)
(K2 = if the reaction is bimolecular from), in eq (4) A and B are concentrations but for very dilute
solution we take activity ( as in a reaction all molecules do not take part, these are only the active
masses which are involved in a reaction).
Activity is directly related with concentration but activity is not equal to concentration
a  C and a = C where  is called activity coefficient and can also be represented as 
By replacing concentration eq (1) can be represented as K#a = / eq (5a) and by putting
activity coefficient in eq (1) can also be written as K#a = X [X ]/ A[A]. B[B]
# #
and also
[X ]/[A][B]= K a/
# #
X /
#
A. B = K a.
#
A. B/ X
#
eq (5b). Now comparing eq (5b) with (1) we get
[K#] = K#a. A. B/ X
#
eq (6) now put the eq (6) in eq (3) to get eq (7) as
= K#a. [A][B] = K2# [A][B] eq (8) ( as K2# = Ka#)
Equation (4) is in term of concentration where as eq (8) is in term of activity.
Now again starting from eq (3) we know that =
[ ]
eq (9) Now putting the value of from eq (5a) into eq (9) we obtained
K2= [ ] eq (10). As a = C so rearrange eq10 as K2= eq (11). Putting
the value of X# from eq (1) we get K2= eq (12)
At infinite dilution the activity coefficient value become equal to 1. Eq (12) becomes as K2= Ko.
T. As Ko is constant so K2 is directly proportional to temperature which indicate that rate
constant or rate of reaction depends on temperature. The factors of activity can be calculated by
Deby-Huckle equation
-log = Zi2 μ1/2/1+αμ1/2. Here α and are constants and its value is 0.51 at 25oC (in aqueous
solution)
As a reaction is incomplete without thermodynamic parameters so applying thermodynamic
parameters as given below.
In term of Gibbs free energy of the activated complex (kinetic approach)

Gibbs free energy is the energy associated with a chemical reaction that can be used to do some
useful work (it tell us about the spontaneity of a reaction). Under conditions of constant
temperature and pressure, chemical change will tend to occur in whatever direction leads to a
decrease in the value of the Gibbs free energy. This means, of course that if the total free energy
G of a mixture of reactants and products goes through a minimum value as the composition
changes, then all net change will cease the reaction system will be in a state of chemical
equilibrium.
The free energy (available energy) G is a quantity that becomes more negative during the course
of any natural process. Thus as a chemical reaction takes place, G only falls and will never
become more positive. Eventually a point is reached where any further transformation of
reactants into products would cause G to increase. At this point G is at a minimum (see the plot
below), and no further net change can take place; the reaction is at equilibrium. Look in a
molecule of glucose inside a human body. The entropy is minimum; the enthalpy is maximum
and what about the free energy (available energy). When respiration takes place then glucose
molecule is break down into CO2 and H2O so enthalpy decreases and entropy increases with the
release of energy (called available energy) so Gibbs free energy also decreases (goes to
negative). The energy released is used for useful work of human body.
ΔG = ΔH-TΔS
If ΔG< 0 reaction is spontaneous (farward direction), if ΔG>0 reaction is non spontaneous
(backward direction) and if ΔG = 0 reaction is at equilibrium.
( )
(In trem of Ginbbs free energy.
In term of enthalpy and entropy of the activated complex (thermodynamic approach).
It is noteworthy that kinetics and thermodynamics depends upon the media of the reaction. As
we can see that for solid the equation E = ΔH+RT assume the form E = ΔH (RT = 0), as there are
minimum motions (rotational etc) of the molecules within a crystal and for solution E = ΔH+RT.
The difference is very minor. E = 10-20kcal/mol and RT = 0.6 Kcal/mol. It mean rate of reaction

is affected by activation energy to a graeter extent and not by ΔH#. In the same way ΔG# may be
negative or positive depending upon the charges of the reactants at transition state and solvation.
Effect of entropy of activated complex (ΔS#)/How to determine the entropy of activated

complex with respect to reactants, solvent and product.
As during a reaction in solution charges play its role. ΔS# is called entropy of activation, which is
defined as the total entropy change of the reactants and solvent. Entropy may be positive or
negative, it depends whether entropy of activation is increased or decreased. The entropy of
activation is positive when entropy of activation of the activated complex is greater than
reactants and entropy of activation is negative when entropy of activation of the activated
complex is smaller than the reactants.
Figure 2: solvation process during a reaction

It can be determined from the charges on the reactants and solvent. If the charges on the reactants
are opposite then the charges 0n the activated complex is less and hence less salvation and
entropy of activated complex will be greater. The entropy of activation of the activated complex
(ΔS#) will be positive as less solvation would occur around the activated complex and the
activated complex will be in order as compared to the reactants. If the reactants are of same

charge then entropy of activated complex will be negative because less salvation would occur
(Fig.2).
Differences between transitions sate and intermediate
Transition state
The highest energy level where activated complex reside in the energy profile diagram.
Activated complex
The chemical species in a chemical reaction that are always in equilibrium with the reactants but
not with the product. Energy of the activated complex is higher than the reactants and dissociate
to the product. It tells us about the rate of a reaction. Activated complex can reside anywhere on
the energy profile diagram Fig (1).
Intermediate
A specie that is present at energy minima at the energy profile diagram (Fig 1). An intermediate
can be isolated (organic chemistry) to elucidate the structure and mechanism of reaction can be
suggested but as the intermediate in inorganic reactions are shortly lived and cannot be isolated
(inorganic chemistry) so mechanism cannot be determined. Determination of intermediate is
necessary to suggest reaction mechanism; therefore, different techniques are used. i.e
spectroscopy, these techniques are useful up to some extent but for complete characterization
some kinetics rules are incorporated.
Figure 3: Intermediate and transition state: Reaction profile diagram for dissociative and
associative reactions mechanism
How structure of intermediate or activated complex can be determined

The structure of an intermediate can be determined by the entropy. If entropy of the reaction is
equal to entropy of the activated complex (ΔSraection = ΔS#activated complex). The structure of the
intermediate will be more similar to the structure of the product. Activated complex can be
determined by using Arhenius equation which tells us about the activation energy. Once
activation energy has been calculated, it means we are very close to the activated complex.
Where A is called Arhenius consttant.
Lnk = lnA +
slop = -Ea
2.303RT
Where K = rate constant lnk
Ea = - slopx 2.303RT
A = Arhenius constant
1/T
Ea = activation energy
T = absolute temperature
But the problem is that only energy of activated complex has been determined and no structural
informations are available from this activation energy. For determination of structure entropy can
be used. If ΔSraection = ΔS#activated complex then structure of the activated complex would be like the
product but if ΔSraection ≠ ΔS#activated complex then structure of the activated complex would be like
that of reactants. eg. If entropy is not same.
[Co (NH3)5Cl]2+ + -OH [Co (NH3)5OH]2+
ΔSreaction = -1.0 cal/deg.mo and ΔS#activated complex = +37 cal/deg.mol
In this case structure is almost unknown and difficult to determine. This reaction is not simple
bimolecular reaction but it is very much complicated due to
i. The role of solvent
As we do not know about the nature of the solvent so very difficult to determined this reaction.
ii. Role of stoichiometry

If stoichiometry and rate law are not reinforcing each other this means reaction is not simple so it
will means that stoichiometry and rate law are not according to our theory.
How equilibrium is set up between reactants and products in gas phase reaction
In gas phase reaction the equilibrium is set up between reactants and products. In gas phase
reaction there is 99.8% empty space but in solution the equilibrium is between reactants and
activated complex. In solution there is 50% empty space, the remaining space is occupied by the
solvent pocket. When reactants A and B come for collision in the reaction medium these are
hindered by the solid particles of the reactants and solvent as well. If accidently A (ox) and B
(red) comes in these solvent particles collision takes place which lead to the reaction. It remains
for 10-12 sec in the solvent pocket. As the energy of A and B are higher and when it come close
in the solvent pocket then the thermal energy is increased to the extent to cross the barrier of
energy; collision occurs and product is formed. Reaction speed depends on the activated
complex.
Rate law and mechanism
Mechanism is defined as an actual pathway through which a reaction proceeds. Or a pathway in

which we study all the stages between reactants and products. Mechanism depends upon
kinetics. On the basis of mechanism inorganic reactions are divided into two types
1. Simple reactions
A reaction in which only one transition state is involved.

1. Complex reaction
A reaction in which more than one transition stages are involved.
Rate law
The rate law is the experimentally determined dependence of the reaction rate on reagent
concentration. It has the following general form
aA + bB cC + dD
dx/dt (rate) = k [A]a [B]b
Where k is proportionality constant called the rate constant. The exponents’ m and n are
determined experimentally from the kinetic study and have no necessary relationship to the
stoichiometric coefficients in the balanced chemical reaction. The rate law may contain species
that do not appear in the balanced reaction and may be the sum of several terms for different
reaction pathways.
Order of rate law
The order of the rate law is the sum of the exponents in the rate law. Here a+b is called order of
reaction it ranges from –ive to 3. For example if a =1 and b = -2 in above equation, the rate law
has an overall order of -1. If a =2 and b=1 then the overall order would be 3. However, except in
the simplest cases, it is best to describe the order with respect to individual reagents. As we know
that rate depends upon the concentration of solvent and stoichiometry, when rate (kinetics) of
reaction changes then structure of intermediate also changes and when stoichiometry changes
then rate law is also affected which effects rate of reaction. Depending upon the speed of various
steps involved in a chemical reactions, reaction may be classified as
1. Simple reaction
If the speed of different steps in a chemical reaction is same than it is called simple complicated
reaction.
2. Complicated reaction

If the speed of different steps in a reaction is different than the reaction is called complicated
reaction. As we know that in a reaction each step is different, so rate law depends on the slowest
step and sometime rate law is determined by more than one step. To evaluate the rate
determining step and eliminate the unnecessary steps steady state approximation is used.
H2O2 + 3I- +2H+ 2H2O + I3-
Experimental rate law.
[ ]
H+ has no role because the reaction is complexed as the mechanism consists of more than one
step.
H2O2 + I- H2O + IO- (i)
IO- + H+ HOI (ii)
HOI + H+ + I- H2O + I2 (iii)
I- + I2 I3- (iv)
It is a complicated reaction and each step is different so rate law depends upon the slowest step
(i) which is determined from the mechanism and it is very difficult in inorganic reaction. It is
almost impossible experimentally but theoretically it can be found by the assumption of
Bodestien for rate law determination in case a reaction consists of more than one step. This
approximation is called steady state approximation. This approximation is then compared with
the experimental calculations if the steady state approximation agree with the experimental rate
law the mechanism is true otherwise false. For a complex reaction more than one reactions takes
place for a single product formation so more than one constant are possible and 1st step rate
constant is very slow than the 2nd and so on (k1<<<k2). This law is applicable to reaction where
intermediate are unstable so in the last equation there must not be an intermediate. The main
theme of steady state approximation is:
1. It is applicable to those reactions where intermediate is unstable

2. Rate of intermediate is kept constant/negligible (means intermediate is considered

stationary/steady that is why it is called steady state approximation)
3. 1st step is the slowest step (k1<<<k2)
4. Product of 1st step (K1 will be reactants for the 2nd reaction (step with k2) and so on.
5. At the end of the steady state approximation there must not be any intermediate in the
equation.
Steady state approximation

Reaction:
Cr (III) + 3Co (III) → Cr (VI) + Co (II)

k1
Ag (I) + 3Co (III) Ag (II) + Co (II)
k2
Ag (II) + 3Cr (III) → Ag (I) +Cr (IV)
Ag (II) + Cr (IV) → Ag (I) +3Cr (V)
Ag (II) + Cr (V) → Ag (I) +3Cr (VI)

According to steady state approximation
Rate of formation of a substance = rate of disappearance of a substance.
As we know that the only stable states of chromium are Cr (III) and Cr (VI), rest of the state of
chromium is intermediates. Likewise the stable state of silver is Ag (I), Ag (II) is an intermediate
so it should not be present in the end result. As far as cobalt is concerned it is stable in Co (II)
and Co (III) states and rests of its states are unstable.
The main approximation is:
Rate of formation of Cr (VI) = Rate of disappearance of Cr (V)
]=
= (1)
As rate of formation of Cr (V) consist of different steps that give us Cr (VI) and Cr (V) is also an
intermediate and must be eliminated also so in this case
Rate of formation of Cr (V) = Rate of disappearance of Cr (V)
]=
OR

Rate of formation of Cr (V) = Rate of formation of Cr (V)-Rate of disappearance of Cr (V) = 0
]- =0
So ] (2)
Simplification of Eq (2) we get the following result

]
= Cr (V) = (2a)
So Cr (V) has been eliminated (evaluated)

Apply the same procedure to eliminate Cr (IV) intermediate
Rate of formation of Cr (IV) = Rate of disappearance of Cr (IV) OR
Rate of formation of Cr (IV) = Rate of formation of Cr (IV) - Rate of disappearance of Cr (IV) =
0
]- =0 (3)
]=
= Cr (IV) = (3a)
To eliminate Cr (IV) put eq (3a) in eq (2a).
= Cr (V) = = (4)
Now we got the value of Cr (V). put the value of Cr (V) into eq (1)
= ]= = ]
k3[Cr (III)][Ag(II)] (5)
Now it is the turn of the Intermediate Ag (II)
Rate of formation of Ag (II) = Rate of formation of Ag (II) - Rate of disappearance of Ag (II) = 0

]-
= 0
(6)
From eq (2) we know that ]
And also from eq (3) ]=
So ]=
By putting the value ] in eq (6) instead of K4 and K5 we get the following

equation:
]-
= 0
= ]- 3
= ]= 3
= ]=
(7)
Now by putting the value of eq (7) into eq (5) we get the final equation without intermediate.
k3[Cr (III)]
Hence the final result do not contains any intermediate.
If we plot a graph between intensity and wavelength we see that by increasing the concentration
of Cr (VI) the intensity also increases at an optimized wavelength of 478nm. At this wavelength
Ag (I) which act as a catalyst also absorb but are negligible.

 = 475
Assignment: steady state approximation on S2O8-(Peroxodisulphate)
When a reaction involves one or more intermediates, the concentration of one of the
intermediates remains constant at some stage of the reaction. Thus, the system has reached
a steady-state, hence the name of the technique is called steady state approximation.
Example-2
Oxidation by peroxodisulphate (S2O8-2) provides an example of Steady State Approximation in
handling complicated chain mechanism. Uncatalyzed reaction by peroxodisulphate commonly
described by rate law showing a first order dependence on (S2O8-2) but zero order dependence on
reducing agent. The aqueous decomposition of peroxodisulphate is first order. A purposed
mechanism must account of this. The following scheme has been purposed in which S represent
an oxidizable substrate, R is a radical derived from S, and p is a product of reaction. In this
reaction S and S2O82- are used.
The main theme of this reaction is the decomposition of S 2O82-. So all the intermediate species
must not be present in the end rate expression.
S 2O82- → 2SO4-
SO4- + H 2 O → OH + HSO4-

OH + S → OH - + R
R + S2O82- → P + SO42- + SO4-
R + SO42- → P + SO42-
The rate of decomposition of (S2O8-2) and substrate are given by
-d[S2O8-2]/dt=k1[S2O8-2] + k4[R][S2O8-2] (1)
-d[S]/dt=k3[OH][S] (2)
Rate of formation of radials SO4-, R and OH are given by
d[SO4-]/dt=2k1[S2O8-2]-k2[SO4-]+k4[R][S2O8-2]-k5[R][SO4-] (3)
d[R]/dt=k3[OH][S]- k4[R][S2O8-2]- k5[R][SO4-] (4)
d[OH]/dt=k2[SO4-]- k3[OH][S] (5)
By the steady state approximation the concentrations of these radicals are constants.
d[SO4-]/dt= d[R]/dt= d[OH]/dt=0 (6)
Elimination of [OH]
equation 5 in the light of eq 6 can be written as

d[OH]/dt = k2[SO4-]- k3[OH][S]
0 = k2[SO4-]- k3[OH][S] (when d[OH]/dt = 0)
k2[SO4-] = k3[OH][S]
[S] = (7)
Elimination of [S]
By putting the value of [S] from equation 7 to equation 2
-d[S]/dt= k2.k3[SO4-][OH]/k3[OH]
-d[S]/dt= k2[SO4-] (8)
Or from eq 7 into eq 4 to give k2[SO4-]. As k2[SO4-] = k3[OH][S], so replacing k3[OH][S] in eq 4

with k2[SO4-].
d[R]/dt = K2[SO42-]- k4[R][S2O82-]-K5[R][ SO42-] = 0 (9)
Addition of equation 3 and 9

2k1[S2O8-2]-k2[SO4-]+k4[R][S2O8-2]-k5[R][SO4-] + K2[SO42-]- k4[R][S2O82-]-K5[R][ SO42-] = 0
2k1[S2O8-2]- 2k5[R][SO4-] = 0
k1[S2O8-2] = k5[R][SO4-] (10)
Similarly by subtracting 9 from 3
2k1[S2O8-2]-k2[SO4-]+k4[R][S2O8-2]-k5[R][SO4-]- K2[SO42-]- k4[R][S2O82-]-K5[R][ SO42-] = 0
2k1[S2O8-2]-2 k2[SO4-] - 2k4[R][S2O8-2] = 0
2 k2[SO4-] = 2[k1[S2O8-2]+ k4[R][S2O8-2]
k2[SO4-] = k1[S2O8-2]+ k4[R][S2O8-2] (11)
By comparing equation 8 and 11
d[S]/dt= k1[S2O8-2]- k4[R][S2O8-2] (12)
By comparing equation 12 and 1
-d[S]/dt = -d[S2O8-2]/dt (12a)
From equation 10
[SO4-]= k1[S2O8-2]/k5[R] (12b)
Elimination of [SO4-] from equation 11
By putting eq (12 b) into 11 we can get an equation as
k2[SO4-] = k1[S2O8-2]- k4[R][S2O8-2] = k2. k1[S2O8-2]/k5[R]= k1[S2O8-2]- k4[R][S2O8-2]
k1.k2/k5[R] = k1+ k4 [R] (13)
rearranging eq 13
k1.k2/k5= [k1[R] + k4 [R]2]

k4 [R]2] + [k1[R]-k1.k2/k5= 0
Elimination of [R]
[R] is obtained by solving quadratic equation.
a = k4, b = k1, c = -k1.k2/k5
√ √
R= =
[R] = (13)
Putting the value of [R] into equation 1
-d[S2O8-2]/dt=k1[S2O8-2] + k4[R][S2O8-2]
-d[S2O8-2]/dt = k1[S2O8-2] + k4[ [ S2O8-2]
-d[S2O8-2]/dt = k1[S2O8-2] + [ [ S2O8-2]
= [S2O8-2] [k1+ [ 1/2
= [S2O8-2][ 1/2
= 1/2[S2O8-2][ 1/2
If k1 = 0 then = 1/2[S2O8-2][ 1/2
[S2O8-2]/dt = [S2O8-2] [k1.k2 k4]
As observed rate is independent of the concentration of substrate but it is first order in S2O82-
concentration.

Factors effecting rate of inorganic reactions
1. Effect of solvent and salvation of ions on the rate of inorganic reactions
Inorganic reactions are mostly carried out in water (polar solvent) because it is universal solvent,
easily available, dielectric constant is compatible with inorganic substances, in case it is not
compatible than reactants will not be soluble in the solvent. As most of the coordinated
complexes proceed through substitution reaction in which water is mostly used as a solvent but
instead of our desired product. There are 100 % chances of aquo complexes which is a major
problem.now question arise how to decide whether the raction in such type of situation is SN 1,
SN2 or SN1CB. To solve this dilemma, let’s consider a general substitution reaction of octahedral
comples.
[CoA5X] 2+ + Y- [CoA5Y] 2+ + X-
When H2O is used along with Y- then there are 100% chances of the formation of aquo
complexs.
[CoA5X] 2+ + H2O ⇔ [CoA5 (H2O] 3+ + X- (i)
[CoA5 (H2O] 3+ + Y- → [CoA5Y] 2+ (ii)
Rate α [[CoA5X] 2+[ H2O]
The end product in both reactions are same then why H2O is problematic, it is because of the fact
that in the rate equation (kinetic study) water is involved which means rate of reaction depends
on water and complex specie but independent as far as the concentration of desired ligand Y- is
concerned which is a major problem related with the synthesis of complex in aquos medium.
Influences of water in a chemical reaction through different ways/or evaluation of the rate
is a problem)/or Evaluation of H2O
Evaluation of the rate of aquo complexes is very difficult. we are not certain whether reaction are
SN1, SN1CB or SN2 (in inorganic chemistry the reaction is not perfectly SN1 like in organic
chemistry but SN1 type).

In case it is SN1 then the product will follow the following rout.
[CoA5X] 2+ ⇔ [CoA5] 3+ + X- (i)
[CoA5] 3+ + H2O - → [CoA5 (H2O] 3+ (ii)
In case the reaction proceed through SN2 mechanism
[CoA5X] 2+ + H2O⇔ [CoA5 (H2O] 3+ + X- (i)
[CoA5 (H2O] 3+ + Y- → [CoA5Y] 2+ (ii)
Rate α [CoA5X] 2+[ H2O]
Now consider a specific example
i. SN1
a. Co (NH3)5Cl]2+ ⇔ Co (NH3)5]3+ + Cl- Co (NH3)5H2O]3+
Rate = Ka[Co (NH3)5Cl]2+]
ii. SN2
b. Co (NH3)5Cl]2+ + H2O ⇔ Co (NH3)5Cl.H2O]3+ Co (NH3)5H2O]3+ + Cl-
Rate = Kb[Co (NH3)5Cl. H2O]2+]
iii. SN1CB (Acid base reaction as a problem)
c. Co (NH3)5Cl]2+ + H2O → Co (NH3)5H2O]3+ H2O → Co (NH3)5OH]2+ + H3O+

Rate = //K[Co (NH3)5Cl]2+ as H2O is conc is constant so Kb.k = //K
So different mechanism is followed by this particular reaction in the presence of H2O. Here H2O
inside the coordination sphere act as an acid and outside the coordination sphere as a reactant act
as a base. We can also say that hydrolysis of H2O takes place (H2O ↔ -OH + H3O+).
During a reaction metals ions and its counter reacting ion must be free so that it may easily react
with each other. There must not be salvation of these ions as salvation hinders the reaction

between ions (Co3+ and Cl-). So 3rd interfering species must be avoided for smooth and easy
reaction to take place ( here H2O is a 3rd interfering species). If a direct reaction between the ions
takes place then it would be as follow
Co3+ + Cl- CoCl32+
But as we know that ions are not bare in aquos medium and the complex is an aquo complex,
during substitution water molecule is replaced from the coordination sphere by the entering
ligand (Cl- in this case). Now the problem for such type of reactions is the uncertainty of the
number of water molecules (extent of hydration), though know in some cases (n=6 for octahedral
type complexes). It is solved by isotopic hydration method in which oxygen of water molecule
labeled as O18. On mixing solution of Cr3+ aquo complex with H2O18, a slow isotopic exchange
takes place.
[Cr (H2O) n] 3+ + H2O18 ⇔ [Cr (H2O18] 3+ + H2O
Which can be followed either the decrease in the amount of isotopically labeled H2O18
concentration or increase in concentration of isotopically labeled in the complex by sampling the
complex at various times by distillation procedure. The isotopic exchange has a half life of about
40hrs at 25oC. For a given solution of Cr3+ the number of unbound water molecules can be
calculated from the isotopic dilution which results within a short time of mixing with O18
containing solvent. The number of bound water molecules is the difference between this value
and the total number present. Let the total number of water molecules are bound to the metal ions
are unknown. At mixing of the isotopic water, say 20 molecules and performing distillation, we
get 6 molecules of unlabeled water which was exchanged by the labeled water. The difference
between 20-6 = 14 (O18). Hence it can be confirmed either by calculating the number of isotopic
water molecules left or by the unlabeled water (O16) removed by exchanging with O18. Ions of
Cr3+ to molecules of bound water were found to be in the proportion of 1 to 6. The number of
water molecules comprising the primary coordination shell of metal ion has rarely beenso
exactly defined for the case of Cr3+. The determination becomes more difficult as the exchange
rate increases. However by employing a flow technique, a value of 6 for the hydration number
can be obtained (as obtained for Al3+).

How to avoid/ evaluate the problem of H2O entering into a chemical reaction/ what is the
possible solution of the interference of H2O in inorganic reactions.
To tickle the problem of H2O that has unwanted interference in substitution reactions in
octahedral complexes discussed above. We should use the following solvents.
1. Polar solvent
2. Non-polar solvent
These solvents could be used but the 1st problem is the dielectric constant which affect the
solubility. If dielectric constant is small as of organic solvent then metal ion will aggregates or
associate more easily, which is not demanded in complex formation reactions as interpretation of
data is difficult. So it is probably true that kinetic study of the reactions of metal ions in such
media (non aqueous) is worthless and can be used for non kinetic study. Keeping in view this
entire factor of using non aqueous medium and also the shortcoming of H2O but still we prefer
water as a solvent because it is cheap, easily available and have high dielectric constant.

Kinetics and Mechanisms of Inorganic Reactions in Solution

Uploaded by

Copyright:

Available Formats

Kinetics and Mechanisms of Inorganic Reactions in Solution

Uploaded by

Document Information

Original Title

Copyright

Available Formats

Share this document

Share or Embed Document

Sharing Options

Did you find this document useful?

Is this content inappropriate?

Copyright:

Available Formats

Kinetics and Mechanisms of Inorganic Reactions in Solution

Uploaded by

Copyright:

Available Formats

Hussain Ullah

Kinetics and mechanisms of inorganic reactions in solution

Never lose hope until it’s over, completely

Kinetics and reaction mechanisms in inorganic chemistry

(With respect to reactants)

(With respect to products)

Never lose hope until it’s over, completely

Never lose hope until it’s over, completely

Theories of reaction rates

Figure 1 Reaction profile showing position of transition and intermediate state.

Never lose hope until it’s over, completely

Where x is small change in the concentration of reactants or products.

⇔ →M+N( is an activated complex)

(Rate of disappearance of reactants)

(Rate of appearance of product)

The above equations can be represented schematically as

Never lose hope until it’s over, completely

and we know that the rate of formation of product is

(2) Putting eq (1) in eq (2) eq (3)

as K2 = so eq (3) can be written as (4)

= K#a. [A][B] = K2# [A][B] eq (8) ( as K2# = Ka#)

Equation (4) is in term of concentration where as eq (8) is in term of activity.

Now again starting from eq (3) we know that =

K2= [ ] eq (10). As a = C so rearrange eq10 as K2= eq (11). Putting

the value of X# from eq (1) we get K2= eq (12)

parameters as given below.

In term of Gibbs free energy of the activated complex (kinetic approach)

Never lose hope until it’s over, completely

In term of enthalpy and entropy of the activated complex (thermodynamic approach).

Never lose hope until it’s over, completely

Effect of entropy of activated complex (ΔS#)/How to determine the entropy of activated

Figure 2: solvation process during a reaction

Never lose hope until it’s over, completely

Differences between transitions sate and intermediate

How structure of intermediate or activated complex can be determined

Never lose hope until it’s over, completely

Where A is called Arhenius consttant.

[Co (NH3)5Cl]2+ + -OH [Co (NH3)5OH]2+

ΔSreaction = -1.0 cal/deg.mo and ΔS#activated complex = +37 cal/deg.mol

i. The role of solvent

ii. Role of stoichiometry

Never lose hope until it’s over, completely

Rate law and mechanism

Mechanism is defined as an actual pathway through which a reaction proceeds. Or a pathway in

A reaction in which only one transition state is involved.

Never lose hope until it’s over, completely

A reaction in which more than one transition stages are involved.

dx/dt (rate) = k [A]a [B]b

Order of rate law

Never lose hope until it’s over, completely

H2O2 + 3I- +2H+ 2H2O + I3-

Experimental rate law.

H2O2 + I- H2O + IO- (i)

IO- + H+ HOI (ii)

HOI + H+ + I- H2O + I2 (iii)

1. It is applicable to those reactions where intermediate is unstable

Never lose hope until it’s over, completely

2. Rate of intermediate is kept constant/negligible (means intermediate is considered

Steady state approximation