DESIGN AND MODELING OF BEVEL GEAR

CONTENT
SL INDEX PAGE NO
NO.
1  ABSTRACT 1
 INTRODUCTION 1.1
2  ABOUT DOUBLE RIVETED LAP JOINTS 2
 DOUBLE RIVETED JOINT 2.1
 ADVANTAGES OF DOUBLE RIVETED JOINTS 2.2
 DISADVANTAGES OF RIVETED JOINTS: 2.3
 APPLICATIONS OF DOUBLE RIVETED JOINTS 2.4
 TYPE OF FAILURES IN RIVETED JOINTS: 2.5
3  TYPE OF FAILURES IN RIVETED 3
JOINTS
3.1
PROBLEM

4  TABLE FORM DESIGN DATE 7

HANDBOOK
7.1
CONCLUSION

BEVEL GEAR Page 1

 DESIGN AND MODELING OF BEVEL GEAR

Abstract
This chapter provides an overview of riveted joints. In the majority of
built-up structures the several members are united by riveted joints,
and the strength of the joints is just as important as the strength of
the members themselves. Unfortunately, the strength of riveted
joints cannot be calculated with any degree of certainty, and
practical design usually depends on empirical formulae based on
experience. It is evident that, if the rivets are carrying any load, they
must be acting as stops to check the relative movements of the
plates. But, as long as the friction forces are great enough, there will
be no relative movement, and the rivets will not bear any load; as
soon as slip occurs, the rivets are acted on by shearing forces in the
planes separating the cover plates from the main plates. It is
obvious that a uniform distribution of load among the rivets cannot
be attained unless the line of action of the resultant force acting on
the joint passes through the centroid of the rivet-holes, and, at the
same time, the rivets are symmetrically disposed with regard to the
resultant force

BEVEL GEAR Page 2

 DESIGN AND MODELING OF BEVEL GEAR

Introduction
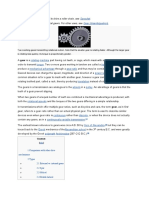
Bevel gears are used to transmit power between two intersecting shafts. There are two common

(a) Straight Bevel Gear (b) Spiral Bevel Gear

The elements of the teeth of the straight bevel gears are straight lines, which converge into a
common apex point. The elements of the teeth of the spiral bevel gears are spiral curves, which
also converge into a common apex point. Involute profile is used for the form of the teeth for
both types of gears. Straight bevel gears are easy to design and manufacture and give reasonably
good service when properly mounted on shafts.

However, they create noise at high-speed conditions. Spiral bevel gears, on the other hand, are
difficult to design and costly to manufacture, for they require specialized and sophisticated
machinery for their manufacture. Spiral bevel gears have smooth teeth engagement, which
results in quiet operation, even at high speeds. They have better strength and are thus used for
high speed-high power transmission.

BEVEL GEAR Page 3

 DESIGN AND MODELING OF BEVEL GEAR

In some cases, bevel gears are classified on the basis of pitch angle. Three types of bevel gears
that are based on pitch angle are as follows:

(i) When the pitch angle is less than 90°, it is called external bevel gear.
(ii) When the pitch angle is equal to 90°, it is called crown bevel gear.
(iii) When the pitch angle is more than 90°, it is called internal bevel gear.

There are certain specific categories of bevel gears. They are as follows:

i. Miter Gears:
When two identical bevel gears are mounted on shafts, which are intersecting at right angles,
they are called "miter gears. They are shown in Figure 2.

Miter gears have the following characteristics:

(i) The pitch angles of pinion and gear of miter gears are same and each is equal to 45°.
(ii) The pinion and gear of miter gears rotate at the same speed.
(iii) The pinion and gear have same dimensions, namely, addendum, dedendum, pitch
circle diameter, number of teeth and module.
(iv) The pinion and gear of miter gears are always mounted on shafts, which are
perpendicular to each other.

BEVEL GEAR Page 4

 DESIGN AND MODELING OF BEVEL GEAR

ii. Crown Gear:

In a pair of bevel gears, when one of the gears has a pitch angle of 90° then that gear is called
'crown' gear. Such bevel gears are mounted on shafts, which are intersecting at an angle that is
more than 90°. The crown gear is equivalent to the rack in spur gearing. The pitch cone of the
crown gear becomes plane. They are shown in Figure 3.

Crown gear arrangement has the following characteristics:

a) The pitch angle of crown gear is 90º.

b) The bevel pinion and crown gear are always mounted on shafts, which are intersecting at
angle more than 90°.

BEVEL GEAR Page 5

 DESIGN AND MODELING OF BEVEL GEAR

iii. Internal Bevel Gears:

When the teeth of bevel gear are cut on the inside of the pitch cone, it is called internal bevel
gear. In this case, the pitch angle of internal gear is more than 90° and the apex point is on the
backside of the teeth on that gear. They are shown in Figure 4. Internal bevel gears are used in
planetary gear trains.

iv. Skew Bevel Gears:

When two straight bevel gears are mounted on shafts, which are non-parallel and non-
intersecting, they are called skew bevel gears. They are shown in Figure 5(b). It is seen that the
apex point of pinion is offset with respect to that of gear.

Skew bevel gears have following characteristics:

1. Skew bevel gears have straight teeth.

2. Skew bevel gears are mounted on nonparallel and non-intersecting shafts.

BEVEL GEAR Page 6

 DESIGN AND MODELING OF BEVEL GEAR

Terminology of Bevel Gears

A bevel gear is in the form of the frustum of a cone. The dimensions of a bevel gear are
illustrated in Figure 6(a) and (b).

The following terms are important in terminology of bevel gears:

i. Pitch Cone Pitch cone is an imaginary cone, the surface of which contains the pitch lines
of all teeth in the bevel gear.
ii. Cone Centre The apex of the pitch cone is called the cone centre. It is denoted by O.
iii. Cone Distance Cone distance is the length of the pitch-cone element. It is also called
pitch-cone radius. It is denoted by AO.
iv. Pitch Angle The angle that the pitch line makes with the axis of the gear, is called the
pitch angle. It is denoted by g. The pitch angle is also called centre angle
v. Addendum Angle It is the angle subtended by the addendum at the cone centre. It is
denoted by a
vi. Dedendum Angle It is the angle subtended by the dedendum at the cone centre. It is
denoted by d.
vii. Face Angle It is the angle subtended by the face of the tooth at the cone centre. Face
angle = pitch angle + addendum angle = g+a.
viii. Root Angle It is the angle subtended by the root of the tooth at the cone centre. Root
angle pitch angle - dedendum angle = g-d
ix. Back Cone The back cone is an imaginary cone and its elements are perpendicular to the
elements of the pitch cone.
x. Back Cone Distance It is the length of the back cone element. It is also called back cone
radius. It is denoted by rb

BEVEL GEAR Page 7

 DESIGN AND MODELING OF BEVEL GEAR

Design Methodology and Procedure for Bevel Gear Problems:

1) Material Selection:
 Select suitable material if not given from Table 12.7. Page No. 234 DDHB
 Identifying weaker part (pinion/gear)
 If the material used for both pinion and gear is same, then the pinion is weaker
 If the material used for both pinion and gear are different, then the strength factor is used
determine the weaker part
 Design is based on weaker part

2) Find Module:
a. If the diameter is known, use Eqns. 12.37 (second part) and 12.7(a)
b. If the diameter is unknown, use formula (1) from previous section
c. Check for induced σ in both the cases
d. If induced > permissible value, design is fail. Hence adopt/change the module and repeat
(2(c))

3)Calculate the dynamic load (F)

4)Calculate the endurance limit (F)

 For safe design Fex> Fa

5)Calculate the wear load (F)

 For safe design. F> Fa
 If Fw< Fd then equate Fw=Fd
 ie, d1bQK= Fd

Find the value of K and choose suitable material for gear and pinion using Table 12.16, Page No.
239 DDHB

Note: If in the problem, diameter is known and z is unknown, calculate m assuming suitable
value of z. After obtaining m, find the value of z again

BEVEL GEAR Page 8

 DESIGN AND MODELING OF BEVEL GEAR

Advantages

 This gear makes it possible to change the operating angle.

 Differing of the number of teeth (effectively diameter) on each wheel
allows mechanical advantage to be changed. By increasing or decreasing the ratio of
teeth between the drive and driven wheels one may change the ratio of rotations
between the two, meaning that the rotational drive and torque of the second wheel
can be changed in relation to the first, with speed increasing and torque decreasing, or
speed decreasing and torque increasing.

Disadvantages

 One wheel of such gear is designed to work with its complementary wheel and no
other.
 Must be precisely mounted.
 The shafts' bearings must be capable of supporting significant forces.

Application
The bevel gear has many diverse applications such as locomotives, marine applications,
automobiles, printing presses, cooling towers, power plants, steel plants, railway track inspection
machines, etc.
For examples, see the following articles on:

 Bevel gears are used in differential drives, which can transmit power to two axles
spinning at different speeds, such as those on a cornering automobile.
 Bevel gears are used as the main mechanism for a hand drill. As the handle of the
drill is turned in a vertical direction, the bevel gears change the rotation of the chuck
to a horizontal rotation. The bevel gears in a hand drill have the added advantage of
increasing the speed of rotation of the chuck and this makes it possible to drill a range
of materials.
 Spiral bevel gears are important components on rotorcraft drive systems. These
components are required to operate at high speeds, high loads, and for a large number
of load cycles. In this application, spiral bevel gears are used to redirect the shaft
from the horizontal gas turbine engine to the vertical rotor. Bevel gears are also used
as speed reducers

BEVEL GEAR Page 9

 DESIGN AND MODELING OF BEVEL GEAR

Conclusion

As can be seen, bevel gears come in various models based on the geometry of the gear plane
and the splines. The straight bevel gear is identical to the zero bevel gear except for the
shape of the spline or teeth. The hypoid bevel gear is identical to the bevel gear except for
the pitch surface of the latter. The adaptation of the geometric form is detected by what the
bevel gear is required for, and what its performance should be within a machine. As of now
we are solved the problem based on the values we design the bevel gear and using the
software anasis analysing the problem based on the result comparing weather the design is
safe or not

A pair of bevel gears transmitting 7.5 kW at 300 rpm is shown in Figure 1. The pressure angle is
20°. Determine the components of the resultant gear tooth force and draw a free-body diagram of
forces acting on the pinion and the gear

Given data
P=7.5KW, N=300rpm, α=20°,D1-=150mm, D2=200mm b=40mm

Using Eqn; find the torque

6 6
9.55∗10 (P) 9.55∗10 (7.5)
T=Mt= n
= 300

Mt=238750N-m =238750N-mm

BEVEL GEAR Page 10

 DESIGN AND MODELING OF BEVEL GEAR

Using Eqn; find the delta 1 and 2

d1 150
tan δ1= d 2 = 200

∴ δ1=36.87°
Using Eqn; find the length
d1 150
L= 2sin δ 1 = 2sin 36.87 ° =125mm

Using relation given in Eqn 12.34(c)

L 125
K2= b = 40 =3.125

Using Eqn 12.349(b)

0.5 0.5
Dm=(1- K 2 )d1=(1- 3.125 )150=126

SOLID EDGE MODEL

BEVEL GEAR Page 11

 DESIGN AND MODELING OF BEVEL GEAR

BEVEL GEAR Page 12

 DESIGN AND MODELING OF BEVEL GEAR

BEVEL GEAR Page 13