Unit-III

Principles of Public –Key Cryptosystems

 Public-key encryption scheme has six ingredients
1. Plaintext: readable message or data
2. Encryption algorithm: performs various transformations on
the plaintext.
3. Public and private keys: pair of keys, one is used for
encryption, the other is used for decryption.
4. Ciphertext: scrambled message
5. Decryption algorithm: accepts the ciphertext and the
matching key and produces the original plaintext.
Public Key Encryption
Authentication
Public-Key Cryptosystem: Secrecy
Public-Key Cryptosystem: Authentication
Classification of uses of public-key
cryptosystems
1. Encryption/Decryption
2. Digital Signature
3. Key exchange
RSA – Rivest-Shamir-Adleman
 Block cipher
 Plaintext and ciphertext are integers between 0 and n - 1
for some n.
 A typical size for n is 1024 bits, that is, n is less than 21024
 Block size is I bits, where 2i < n ≤ 2i+1
 Plaintext block M and ciphertext block C
C = Me mod n
M = Cd mod n
RSA Algorithm
RSA Example
 For this example, the keys were generated as follows
1. Select two prime numbers, p = 17 and q = 11
2. Calculate n = pq = 17 × 11 = 187
3. Calculate Φ (n) = (p - 1)(q - 1) = 16 × 10 = 160
4. Select e such that e is relatively prime to Φ (n) = 160 and less
than f(n); we choose e = 7
5. Determine d such that de = 1(mod 160) and d < 160 The
correct value is d = 23, because 23 × 7 = 161 = (1 × 160) + 1;
d can be calculated using the extended Euclid’s algorithm
6. The resulting keys are public key PU = {7, 187} and private key
PR = {23, 187}
 For encryption, we need to calculate C = 887 mod 187
 For decryption, we calculate M = 1123 mod 187
Key Management
 The distribution of public keys
 The use of public-key encryption to distribute secret keys
Distribution of public keys
1. Public announcement
2. Publicly available directory
3. Public-key authority
4. Public-key certificates
1. Public announcement
 Participant can send his or her public key to any other
participant or broadcast the key to the community at
large

 Convenient but Anyone can forge such a public

announcement and pretend to be user A and send a
public key to another participant or broadcast such a
public key
2. Publicly available directory
 The authority maintains a directory with a {name, public
key} entry for each participant.
 Each participant registers a public key with the directory
authority.
 Registration is in person/secure authenticated communication.
 A participant may replace the existing key with a new one
at any time
 Participants could also access the directory electronically.
3. Public-key authority
1. A sends a timestamped message to the public-key authority
containing a request for the current public key of B.
2. The authority responds with a message that is encrypted using
the authority's private key, PRauth
 B's public key, PUb which A can use to encrypt messages destined for B
 The original request, to enable A to match this response
 The original timestamp, so A can determine that this is not an old message
3. A stores B's public key and also uses it to encrypt a message to B
containing an identifier of A (IDA) and a nonce (N1), which is used
to identify this transaction uniquely.
4. B retrieves A's public key from the authority in the same manner
as A retrieved B's public key.
6. B sends a message to A encrypted with PUa and containing A's
nonce (N1) as well as a new nonce generated by B (N2)
 presence of N1 in message assures A that the correspondent is B.
7. A returns N2, encrypted using B's public key, to assure B that its
correspondent is A.
3. Public-key authority
4. Public-key certificates
 Use certificates that can be used by participants to exchange
keys without contacting a public-key authority
 Certificate consists of a public key plus an identifier of the key
owner, with the whole block signed by a trusted third party.
 The third party is a certificate authority, such as a government agency or
a financial institution, that is trusted by the user community
 A user can present his or her public key to the authority in a secure
manner, and obtain a certificate
 The user can then publish the certificate
 Anyone needed this user's public key can obtain the certificate and
verify that it is valid by way of the attached trusted signature
 A participant can also convey its key information to another by
transmitting its certificate
 Other participants can verify that the certificate was created by the
authority
Public-key certificates
Simple Secret Key Distribution
1. A generates a public/private key pair {PUa, PRa} and
transmits a message to B consisting of Pua and an identifier
of A, IDA.
2. B generates a secret key, Ks, and transmits it to A,
encrypted with A's public key.
3. A computes D(PRa, E(PUa, Ks)) to recover the secret key.
Because only A can decrypt the message, only A and B will
know the identity of Ks.
4. A discards PUa and PRa and B discards PUa.
Diffie-Hellman Key Exchange
Diffie-Hellman Key Exchange
Authentication Requirements
 Attacks identified are
1. Disclosure
2. Traffic analysis
3. Masqurade
4. Content modification
5. Sequence modification
6. Timing modification
7. Source repudiation
8. Destination repudiation
 Measures to deal with items 3 through 6 in the foregoing list are
generally regarded as message authentication.
 Message authentication is a procedure to verify that received
messages come from the alleged source and have not been altered.
 Message authentication may also verify sequencing and timeliness.
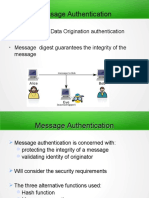
Authentication Functions
 Any message authentication or digital signature
mechanism has two levels of functionality.
 At the lower level, there must be some sort of function
that produces an authenticator: a value to be used to
authenticate a message.
 This lower-level function is then used as a primitive in a
higher-level authentication protocol that enables a
receiver to verify the authenticity of a message.
Authentication Functions
 Functions that may be used to produce an authenticator.
These may be grouped into three classes
1. Message encryption: The ciphertext of the entire message
serves as its authenticator
2. Message authentication code (MAC): A function of the
message and a secret key that produces a fixed-length value
that serves as the authenticator
3. Hash function: A function that maps a message of any length
into a fixed-length hash value, which serves as the
authenticator
1. Authentication Functions: Message
Encryption
2. Authentication Functions: MAC
 Message authentication
2. Authentication Functions: MAC
 Message authentication and confidentiality: authentication
tied to plaintext
2. Authentication Functions: MAC
 Message authentication and confidentiality: authentication
tied to ciphertext
3. Authentication Functions: Hash Functions
 Variety of ways in which a hash code can be used to
provide message authentication
1. The message plus concatenated hash code is encrypted
using symmetric encryption.

2. Only the hash code is encrypted, using symmetric

encryption
3. Authentication Functions: Hash Functions
3. Only the hash code is encrypted, using public-key
encryption and using the sender's private key.

4. If confidentiality as well as a digital signature is desired,

then the message plus the private-key encrypted hash
code can be encrypted using a symmetric secret key.
3. Authentication Functions: Hash Functions
5. It is possible to use a hash function but no encryption
for message authentication.

6. Confidentiality can be added to the approach of (5) by

encrypting the entire message plus the hash code.
Message Authentication Codes
 A MAC, also known as a cryptographic checksum, is
generated by a function C of the form
MAC = C(K, M)
 where
 M is a variable-length message,
 K is a secret key shared only by sender and receiver, and
 C(K,M) is the fixed-length authenticator.
 The MAC is appended to the message at the source at a time
when the message is assumed or known to be correct.
The receiver authenticates that message by recomputing
the MAC.
Requirements of MACs
 MAC function should satisfy the following requirements:
 If an opponent observes M and C(K, M), it should be
computationally infeasible for the opponent to construct a
message M' such that C(K, M') = C(K, M).
 C(K, M) should be uniformly distributed in the sense that for
randomly chosen messages, M and M', the probability that C(K, M)
= C(K, M') is 2n, where n is the number of bits in the MAC.
 Let M' be equal to some known transformation on M. That is, M' =
f(M). For example, f may involve inverting one or more specific
bits. In that case, Pr[C(K, M) = C(K, M')] = 2n.
Hash Functions
 A hash value h is generated by a function H of the form
h = H(M)
 where
 M is a variable-length message and
 H(M) is the fixed-length hash value.
 The hash value is appended to the message at the source
at a time when the message is assumed or known to be
correct.
 The receiver authenticates that message by recomputing
the hash value. Because the hash function itself is not
considered to be secret, some means is required to
protect the hash value
Security of Hash Functions and Macs
 As with symmetric and public-key encryption, we can
group attacks on hash functions and MACs into two
categories:
1. Brute-force attacks and
2. Cryptanalysis
Security of Hash Functions and Macs
 Brute-Force Attacks
 Hash Functions
 The strength of a hash function against brute-force attacks depends
solely on the length of the hash code produced by the algorithm.
Message Authentication Codes
 A brute-force attack on a MAC is a more difficult undertaking
because it requires known message-MAC pairs.
 Cryptanalysis
 The way to measure the resistance of a hash or MAC algorithm
to cryptanalysis is to compare its strength to the effort
required for a brute-force attack.
 That is, an ideal hash or MAC algorithm will require a
cryptanalytic effort greater than or equal to the brute-force
effort.
Digital Signatures
 Message authentication protects two parties who exchange messages
from any third party.
 However, it does not protect the two parties against each other.
Several forms of dispute between the two are possible.
 Suppose that John sends an authenticated message to Mary,
 Consider the following disputes that could arise:
1. Mary may forge a different message and claim that it came from
John. Mary would simply have to create a message and append an
authentication code using the key that John and Mary share.
2. John can deny sending the message. Because it is possible for Mary
to forge a message, there is no way to prove that John did in fact
send the message.
 In situations where there is not complete trust between
sender and receiver, something more than authentication is
needed.
Digital Signatures
 Solution to this problem is the digital signature
 It has the following properties:
 It must verify the author and the date and time of the
signature.
 It must to authenticate the contents at the time of the
signature.
 It must be verifiable by third parties, to resolve disputes.
 Thus, the digital signature function includes the
authentication function
Requirements of digital signature
 The signature must be a bit pattern that depends on the
message being signed.
 The signature must use some information unique to the
sender, to prevent both forgery and denial.
 It must be relatively easy to produce the digital signature.
 It must be relatively easy to recognize and verify the digital
signature.
 It must be computationally infeasible to forge a digital
signature, either by constructing a new message for an existing
digital signature or by constructing a fraudulent digital
signature for a given message.
 It must be practical to retain a copy of the digital signature in
storage.
Digital Signature Process
Two approaches to Digital Signatures