Location via proxy:   [ UP ]  
[Report a bug]   [Manage cookies]                
Scribd Logo
Upload

Welcome to Scribd!

  • 15 views

    LESSON 4.1 Ellipse With Center HK

    Uploaded by

    jarenhndsm.placiego
    This document discusses ellipses including their standard form equation, characteristics, and how to determine properties like foci, vertices, and axes from equations. It provides examples of writing ellipse equations in standard form and determining associated values, as well as writing equations given certain conditions.

    Copyright:

    © All Rights Reserved
    Download as PDF, TXT or read online from Scribd

    LESSON 4.1 Ellipse With Center HK

    Uploaded by

    jarenhndsm.placiego
    15 views11 pages
    This document discusses ellipses including their standard form equation, characteristics, and how to determine properties like foci, vertices, and axes from equations. It provides examples of writing ellipse equations in standard form and determining associated values, as well as writing equations given certain conditions.

    Original Title

    LESSON-4.1-Ellipse-with-center-hk

    Copyright

    © © All Rights Reserved

    Available Formats

    PDF, TXT or read online from Scribd

    Did you find this document useful?

    Is this content inappropriate?

    This document discusses ellipses including their standard form equation, characteristics, and how to determine properties like foci, vertices, and axes from equations. It provides examples of writing ellipse equations in standard form and determining associated values, as well as writing equations given certain conditions.

    Copyright:

    © All Rights Reserved
    Download as PDF, TXT or read online from Scribd
    Download as pdf or txt
    15 views11 pages

    LESSON 4.1 Ellipse With Center HK

    Uploaded by

    jarenhndsm.placiego
    This document discusses ellipses including their standard form equation, characteristics, and how to determine properties like foci, vertices, and axes from equations. It provides examples of writing ellipse equations in standard form and determining associated values, as well as writing equations given certain conditions.

    Copyright:

    © All Rights Reserved
    Download as PDF, TXT or read online from Scribd
    Download as pdf or txt
    of 11

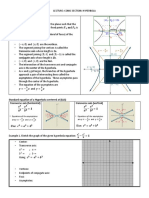
    ELLIPSE

    L E S S O N 4 . 1

    Precalculus Teacher: Ms. Rinalyn D. Saballe


    determine the standard form equation of an
    ellipse with center at (h,k)

    Precalculus Lesson 4: Ellipse


    An ellipse is a set of all
    coplanar points such that the
    sum of its distances from two
    fixed points is constant . The
    fixed points are called the foci of
    the ellipse.

    Precalculus Lesson 4: Ellipse


    Precalculus Lesson 4: Ellipse
    General Equation of ellipse
    𝟐 𝟐
    𝑨𝒙 + 𝑪𝒚 + 𝑫𝒙 + 𝑬𝒚 + 𝑭 = 𝟎
    where, A>0 , C>0 and A≠ 𝐶
    Characteristics of the graph of these ellipses:
    Ellipse with foci on a Ellipse with foci on a
    Center (h,k) line parallel to the x- line parallel to the y-
    axis axis
    (𝑥 − ℎ)2 (𝑦 − 𝑘)2 (𝑥 − ℎ)2 (𝑦 − 𝑘)2
    2
    + 2
    =1 2
    + 2
    =1
    Equation 𝑎 𝑏 𝑏 𝑎
    Where c= 𝑎2 − 𝑏 2 𝑎𝑛𝑑 Where c= 𝑎2 − 𝑏 2 𝑎𝑛𝑑
    a>b 𝑎>𝑏

    Vertices (h±𝑎, 𝑘) (h, k±𝑎)

    Foci (h±𝑐, 𝑘) (h, k±𝑐)


    Characteristics of the graph of these ellipses:
    Ellipse with foci on a Ellipse with foci on a
    Center (h,k) line parallel to the x- line parallel to the y-
    axis axis
    Equation: 𝑦 = 𝑘 Equation: 𝑥 = ℎ
    Direction: horizontal Direction: vertical
    Major axis
    Length: 2a Length: 2a
    Endpoints: (h±𝑎, 𝑘) Endpoints: (h, k ± 𝑎)
    Equation: 𝑥 = ℎ Equation: 𝑦 = 𝑘
    Direction: vertical Direction: horizontal
    Minor axis
    Length: 2b Length: 2b
    Endpoints: (h, k ± 𝑏) Endpoints: (h±𝑏, 𝑘)
    Characteristics of the graph of these ellipses:
    Ellipse with foci on a Ellipse with foci on a
    Center (h,k) line parallel to the x- line parallel to the y-
    axis axis
    Equation: 𝑥 = ℎ ± 𝑐 Equation: y= k±𝑐
    Direction: vertical Direction: horizontal
    2𝑏2 2𝑏2
    Length: Length:
    Latus rectum 𝑎 𝑎
    𝑏2
    Endpoints: (h-c, Endpoints: (h± , 𝑘 −
    𝑎
    𝑏2 𝑏2 𝑏2
    k± ) 𝑎𝑛𝑑 (ℎ + 𝑐, 𝑘 ± ) 𝑐) 𝑎𝑛𝑑 (ℎ ± , 𝑘 + 𝑐)
    𝑎 𝑎 𝑎
    h−𝑎 ≤ 𝑥 ≤ ℎ + 𝑎 h−𝑏 ≤ 𝑥 ≤ ℎ + 𝑏
    Permissible values
    k−𝑏 ≤ 𝑦 ≤ 𝑘 + 𝑏 k−𝑎 ≤ 𝑦 ≤ 𝑘 + 𝑎
    Express each equation of the ellipse in standard form.
    Determine the equation and the length of the major axis, the
    minor axis, and the latus rectum. Draw the ellipse, its foci, and
    vertices.

    a. 𝑥 2
    + 2𝑦 2
    − 2𝑥 + 8𝑦 − 11 = 0
    2 2
    b. 4𝑥 + 𝑦 + 24𝑥 − 10𝑦 + 45 = 0

    Precalculus Lesson 4: Ellipse


    Write the equation of the ellipse in standard form that satisfies
    the given conditions. Draw the ellipse, its foci and vertices.
    a. The center is at (7, -2) , a vertex is at (2, -2) and an endpoint
    of a minor axis is at (7, -6).
    b. The vertices are at (-2,-2) and (-2,8) , and the length of the
    minor axis is 6.
    c. The center is at (4,3), and the length of the horizontal major
    axis is 5, the length of minor axis is 4.

    Precalculus Lesson 4: Ellipse


    END OF DISCUSSION
    H AV E A G R E AT D AY A H E A D : )

    You might also like