EE-311 Ch3 HW Solutions

Solution 3.4

An electric field in free space is E = (5z 3 /  0 ) aˆ z V/m. Find the total charge contained
within a sphere of 3-m radius, centered at the origin. Using Gauss' law, we set up the
integral in free space over the sphere surface, whose outward unit normal is ar :
2 
  0E  n da = 
Q=Ñ  0 5z a z  a r (3)2 sin  d d
3
0

where in this case z = 3cos and (in all cases) a z  ar = cos . These are substituted to
yield
 1
Q = 2  5(3)5 cos 4  sin  d = −2 (5)(3)5   cos5  |02 = 972
0
5

Solution 3.5

Let D = 4 xya x + 2( x2 + z 2 )a y + 4 yza z C/m2 and evaluate surface integrals to find the total
charge enclosed in the rectangular parallelepiped 0  x  2 , 0  y  3 , 0  z  5 m: Of the
6 surfaces to consider, only 2 will contribute to the net outward flux. Why? First consider
the planes at y = 0 and 3. The y component of D will penetrate those surfaces, but will
be inward at y = 0 and outward at y = 3 , while having the same magnitude in both cases.
These fluxes will thus cancel. At the x = 0 plane, Dx = 0 and at the z = 0 plane, Dz = 0 ,
so there will be no flux contributions from these surfaces. This leaves the 2 remaining
surfaces at x = 2 and z = 5 . The net outward flux becomes:

5 3 3 2
=
0 0
D |x = 2 a x dy dz +   D |z =5 a z dx dy
0 0
3 3
= 5 4(2) y dy + 2 4(5) y dy = 360 C
0 0

Solution 3.9

A uniform volume charge density of 80  C/m3 is present throughout the region

8mm  r  10mm . Let v = 0 for 0  r  8mm .

a) Find the total charge inside the spherical surface r = 10 mm: This will be

Hayt/Buck, Engineering Electromagnetics, 8/e. ©2012. The McGraw-Hill Companies

 2  .010 r 3 .010
Q=  0  .008 (80  10−6 )r 2 sin  dr d d = 4  (80  10−6 ) |.008
0 3
= 1.64  10−10 C = 164 pC

b) Find Dr at r = 10 mm: Using a spherical Gaussian surface at r = 10 , Gauss’ law is

written as 4 r 2 Dr = Q = 164 10−12 , or

164  10−12
Dr (10mm) = = 1.30  10−7 C/m 2 = 130nC/m 2
4 (.01)2
c) If there is no charge for r  10 mm, find Dr at r = 20 mm: This will be the same
computation as in part b , except the gaussian surface now lies at 20 mm. Thus
164  10−12
Dr (20mm) = = 3.25  10−8 C/m 2 = 32.5nC/m 2
4 (.02) 2

Solution 3.13

Spherical surfaces at r = 2, 4, and 6 m carry uniform surface charge densities of

20 nC/m2 , −4nC/m2 , and  s 0 , respectively.

a) Find D at r = 1, 3and5 m: Noting that the charges are spherically-symmetric, we

ascertain that D will be radially-directed and will vary only with radius. Thus, we
apply Gauss’ law to spherical shells in the following regions: r  2 : Here, no
charge is enclosed, and so Dr = 0 .

80  10−9
2  r  4 : 4 r 2 Dr = 4 (2) 2 (20  10−9 )  Dr = C/m 2
r2

So Dr (r = 3) = 8.9 10−9 C/m2 .

16  10−9
4  r  6 : 4 r 2 Dr = 4 (2) 2 (20  10−9 ) + 4 (4) 2 ( −4  10 −9 )  Dr =
r2

So Dr (r = 5) = 6.4  10−10 C/m2 .

b) Determine  s 0 such that D = 0 at r = 7 m. Since fields will decrease as 1/ r 2 , the

question could be re-phrased to ask for  s 0 such that D = 0 at all points where
r  6 m. In this region, the total field will be
16  10−9  s 0 (6) 2
Dr (r  6) = +
r2 r2

Requiring this to be zero, we find  s 0 = −(4 / 9)  10−9 C/m2 .

Hayt/Buck, Engineering Electromagnetics, 8/e. ©2012. The McGraw-Hill Companies

Solution 3.16

An electric flux density is given by D = D0 a  , where D0 is a given constant.

a) What charge density generates this field? Charge density is found by taking the
divergence: With radial D only, we have
1 d D
v =   D = (  D0 ) = 0 C/m3
 d 
b) For the specified field, what total charge is contained within a cylinder of radius
a and height b , where the cylinder axis is the z axis? We can either integrate the
charge density over the specified volume, or integrate D over the surface that
contains the specified volume:
b 2 a D0 b 2
Q=
0 0  0
 d  d dz =   D0 a   a  a d dz = 2 abD0 C
 0 0

Solution 3.17

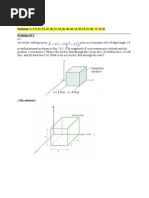
A cube is defined by 1  x, y, z  1.2 . If D = 2 x 2 ya x + 3x 2 y 2a y C/m2 :

a) apply Gauss’ law to find the total flux leaving the closed surface of the cube. We
call the surfaces at x = 1.2 and x = 1 the front and back surfaces respectively,
those at y = 1.2 and y = 1 the right and left surfaces, and those at z = 1.2 and z = 1
the top and bottom surfaces. To evaluate the total charge, we integrate D  n over
all six surfaces and sum the results. We note that there is no z component of D ,
so there will be no outward flux contributions from the top and bottom surfaces.
The fluxes through the remaining four are
1.2 1.2 1.2 1.2
 D  n da = 11 414 42(1.2)
=Q=Ñ
2 4 4 4 3 1 1 4 14 4 2 4 4 4 3
y dy dz + − 2(1)2 y dy dz
2

front back
1.2 1.2 1.2 1.2
+   − 3x (1) dx dz +   3x (1.2) dx dz = 0.1028C
2 2 2 2
11 4 14 4 2 4 4 4 3 11 4 14 4 2 4 4 4 3
left right

b) evaluate   D at the center of the cube: This is

  D =  4 xy + 6 x 2 y  = 4(1.1)2 + 6(1.1)3 = 12.83
(1.1,1.1)

c) Estimate the total charge enclosed within the cube by using Eq. (8): This is
Q B   D |center v = 12.83  (0.2)3 = 0.1026 Close!

Hayt/Buck, Engineering Electromagnetics, 8/e. ©2012. The McGraw-Hill Companies

Solution 3.19

A spherical surface of radius 3 mm is centered at P(4,1,5) in free space. Let

D = xa x C/m2 . Use the results of Sec. 3.4 to estimate the net electric flux leaving the
spherical surface: We use  B   Dv , where in this case   D = ( / x) x = 1C/m3 . Thus
4
 B  (.003)3 (1) = 1.13  10−7 C = 113nC
3

Solution 3.25

Within the spherical shell, 3  r  4 m, the electric flux density is given as

D = 5(r − 3)3 ar C/m2

a) What is the volume charge density at r = 4 ? In this case we have

1 d 2 5
v =   D = 2
(r Dr ) = (r − 3) 2 (5r − 6) C/m3
r dr r

which we evaluate at r = 4 to find v (r = 4) = 17.50 C/m3 .

b) What is the electric flux density at r = 4 ? Substitute r = 4 into the given

expression to find D(4) = 5 ar C/m2

c) How much electric flux leaves the sphere r = 4 ? Using the result of part b , this
will be  = 4 (4)2 (5) = 320 C

d) How much charge is contained within the sphere, r = 4 ? From Gauss’ law, this
will be the same as the outward flux, or again, Q = 320 C .

Solution 3.29

In the region of free space that includes the volume 2  x, y, z  3 ,

2
D= 2
( yz a x + xz a y − 2 xy a z ) C/m 2
z

a) Evaluate the volume integral side of the divergence theorem for the volume
defined above: In cartesian, we find   D = 8xy / z 3 . The volume integral side is
now

Hayt/Buck, Engineering Electromagnetics, 8/e. ©2012. The McGraw-Hill Companies

 3 3 3 8 xy 1 1
 vol  D dv =  2 2 2 z 3
dxdydz = (9 − 4)(9 − 4)  −  = 3.47 C
4 9
b) Evaluate the surface integral side for the corresponding closed surface: We call
the surfaces at x = 3 and x = 2 the front and back surfaces respectively, those at
y = 3 and y = 2 the right and left surfaces, and those at z = 3 and z = 2 the top
and bottom surfaces. To evaluate the surface integral side, we integrate D  n over
all six surfaces and sum the results. Note that since the x component of D does
not vary with x , the outward fluxes from the front and back surfaces will cancel
each other. The same is true for the left and right surfaces, since D y does not vary
with y . This leaves only the top and bottom surfaces, where the fluxes are:
3 3−4 xy 3 3 −4 xy 1 1
 D  dS =  2 2
Ñ 2
dxdy −  
2 2 2
dxdy = (9 − 4)(9 − 4)  −  = 3.47 C
4 9
1 4 4 23 4 4 3 1 4 4 22 4 4 3
top bottom

Hayt/Buck, Engineering Electromagnetics, 8/e. ©2012. The McGraw-Hill Companies