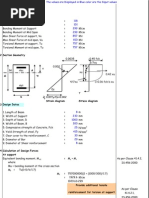
The following steps to be considered while designing 4.

Design of Shear Reinforcement:

the shear reinforcement: i. Shear taken by stirrups =Vus
1. Determine the factored or ultimate design shear force Vus = Vu-𝜏c.bd= 225000-0.596*250*450 Vus=157950
'Vu'. N
2. Determine the nominal shear stress on the section ' 𝜏v' ii. Using 8 mm 2 legged stirrups,
by dividing Vu by bd i.e., v= Vu /bd Asv=2*3.14/4*8^2=100.5mm^2
3. Compute the percentage of tension reinforcement iii. Spacing of stirrups,Sv=0.87.fy.Asv.d/Vus
provided in the section. Based on this percentage of Sv =0.87 x 415 x 100.5 x 450/157950
tension steel, determine the shear strength of concrete Sv=103.38 mm
‘𝜏c’ for the given concrete mix and hence the shear iv. Spacing of nominal shear reinforcement
resisting capacity of the reinforcement concrete section, S= 0.87fy.Asv/0.4b= 0.87x415x100.5/0.4x250
Vc = 𝜏c. bd Sv=362.85 mm
4. Compare v with 𝜏c,max .If 𝜏v> 𝜏c max redesign the 5. Check for Spacing:
cross-section of the beam. The spacing of stirrups should be minimum of the
5. Compare Vu, with Vc (or v with 𝜏c). If Vu <= Vc following:
no shear design is required. Provide nominal i. 0.75 d=0.75 x 450 = 337 mm
reinforcement in the form of vertical stirrups through the ii. 300 mm
beam of the spacing 'Sv’ is given by, iii. 103 mm
Asv/bSv≥ 0.4/0.87fy or Sv ≤ Asv*0.87fy/0.4b iv. 362 mm
Where Asv is the total cross-sectional area of stirrup legs. Provide 2 legged 8 mm & stirrups @ 100 mm c/c
6. If Vu>Vc, provide shear reinforcement for resisting throughout the length the beam
the design shear force ‘Vus’ given by
Vus=Vu-Vc Given: Width of beam, b = 300 mm, Effective depth, d
7. Choose the diameter of the stirrup bar (generally 6, 8, = 600 mm, Reinforcement = 4-25 mm bar, Shear
10 or 12 mm) and the type of stirrup. Determine the force, V = 100kN To Find: Design shear
spacing of the stirrup as follows: reinforcement
1. For vertical stirrups, S=(0.87.fy.Asv.d/Vus) = 1.Area of reinforcement, A = 4 x (π/4) x 25^2= 1963.5
(0.87.Fy.Asv)/( 𝜏v-𝜏c)*b mm²
The maximum spacing of vertical stirrups should not 2. Shear force = 100 kN
exceed 0.75 d or 300 mm. Factored shear force = 1.5 * 100 = 150kN
ii. For inclined stirrups, S=(0.87.fy.Asv.d/Vus)*(sin 3. Nominal shear stress, 𝜏v =150*10^3)/(300* 600) =
alpha+cos alpha) 0.833N /mm ^ 2
ii. For bent up bars, if the tension steel is available for 4. Percentage of area of steel, pt = Ast/(bd)*100 =
shear,bent up the bars from tension steel at 45° at 1963.5/(300 * 600))* 100 =1.09 =1.1%
distance ‘d’ from the support. Compute the shear force 5. Shear strength of concrete, 𝜏c.=0.64 N/mm² (From IS
taken by bent up bars. code 456:2000)
Vs=σsv.Asv.SinAlpha=0.87fy.Asv.Sinalpha Here, A.is 6.Maximum shear strength of concrete, 𝜏c.max =
the total cross-sectional area of bent up bars. Design the 2.8N /m*m^2 (For M20 grade concrete) tau c < tau u <
vertical stirrups for the shear force. Vd=Vus-Vs tau c, max Rightarrow0.64<0.83<2.8 N/mm^ 2 7. Shear
Where, Vus =0.87.f y.Asv.sina Reinforcement:
8.Check whether the spacing of stirrups obtained above i Shear force taken by stirrups, Vux =Vu –
satisfies the code design requirements. tau.bd=150*10^ 3 -0.64*300*600
i.Sv ≯ 0.75d (Spacing governed by the depth of beam). = 34800 N
ii. Sv ≯ (Asv*0.87fy)/0.4b (Based on the minimum shear ii. Use 8 mm diameter 2-legged vertical stirrups
reinforcement) Asv = 2*pi/4*8^2 = 100.6mm ^ 2
iii. Sv </ 60mm (Suggested for better compaction of iii. Spacing of shear stirrups,
concrete) Sv = (0.87.fy.*Asv*d)/Vus = (0.87*415*100.6 *
9. Find the distance from the support up to which the 600)/34800=626.23c/c
design stirrups are required, for the rest of the portion iv. But code requires that,
provides minimum shear reinforcement.
Given: Width, b = 250 mm, Depth, d = 450 m, Area of a. S>/ 300 mm
steel, Ast=4x3.14/4x18^2=1018 mm², Shear force,
V=150 kN b. S >/ 0.75 * d = 0.75*600 = 450mm
To Find: Design shear reinforcement
1. Factored Shear Force (V): Vu=1.5 x 150 v. Minimum shear reinforcement,
Vu=225Kn=225000N [Load factor = 1.5] Asv > 0.4*300*300/0.87*415 =99.71 mm^ 2
2.Nominal Shear Stress 𝜏v=Vu/bd=225000/250x450 8. Hence provide 8 mm 42-legged vertical stirrups @300
𝜏v=2.0 N/mm2 mm c/c
𝜏c,max =2.8 N/mm2 [For M20 concrete] Design Steps for Simply Supported Beam:
𝜏v<𝜏cmax hence OK. 1.Determine design bending moment ( If Mu is not
3 Design Shear Strength of Concrete (t): given) i. Assume suitable value of depth and width (To
i. Percentage of steel, start with, the depth of beam can be assumed as L/12 to
P=100.Ast/bd=100*1018/25*450=0.905% L/15and width may be taken as 1/2 to 1/3 of the depth)
ii.For Pt=0.97% and M20 concrete from IS code 456 ii.Calculate self weight of the beam and determine total
iii. 𝜏c= 0.56+ (0.62-0.56)/1.00-0.75*(0.9-0.75) load (w) by adding imposed loads to self weight.
𝜏c=0.596 N/mm iii. Determine design or factored load (w)
𝜏v>𝜏c hence shear reinforcement is to be provided.
wu = w*gammaf (Yf the partial safety factor for loads reinforcement in the form of longitudinal and transverse
and is taken as 1.5 for DL +LL) reinforcement is provided as explained below:
wu = wx1.5
iv. Calculate the factored moment (Mu) B. Torsional Reinforcement:
For simply supported beam Mu = Wu.L^ 2)/8
For cantilever beam, Mu= (wu.L^ 2)/2 The torsional moment induce diagonal tension in the
2. Determine xu,max/d and Ru beam and it is seen that such beams show spiral cracking
Ru =0.36.f ck.xumax/d (1- (0.42xumax/d ) along the periphery of the section. Therefore, torsional
3. Determine the minimum depth required: um reinforcement is provided in the form of longitudinal bars
dreqd = √ (Mu/( Ru .b) and transverse reinforcement in the form of links or
4. Compare dreod with assumed value of effective depth hoops.
i. If assumed d> deg, then our assumption is correct and
provide the assumed depth and calculate overall 1. Longitudinal Reinforcement: As per IS code 456:2000
ii. If assumed d <dreqd then redesign the section and the longitudinal reinforcement is designed to resist an
repeat.Steps 2 and 3 equivalent bending moment M, which includes the effect
5. Determine the area of steel required: of torsional bending moment
i The effective depth provided is greater than the depth
required for a balanced section, so we are designing an Me=Mu+MT MT=Tu(1+D/b)/1.7
under-reinforced section.The area of steel corresponding
to under reinforced section is calculated from the a If MT<Mu, then longitudinal steel required to resist
following equation: Me, is calculated and distributed as per codal provisions.
Mu = 0.87.fy .Ast.d (1-(Ast.fy/bd.fck)
ii. This area of steel (Ast) should be more than the b.If MT>Mu, then IS code recommends that the
minimum area of steel (As) specified by the code. longitudinal reinforcement should also be provided on
As = (0.85bd)/fyChoose suitable diameter (fie) of steel the compression face of the beam for moment Me’,
bar where
A(phi) = pi/4 *phi^1 M’=MT-Mu
Number of bars required= Ast/Afie In this case, the effect of torsional moment is
v. If instead of an under reinforced section, a balanced predominant and more than the ultimate bending moment
section is designed i.e.,d=dreqd then the area of steel can and is assumed to act opposite to Mu
be estimated directly from the following equation
As = Mu/0.87y(d-0.42xumax) c. Distribution of Longitudinal Reinforcement: The
6. Check for Deflection: longitudinal reinforcement to resist torsion is provided as
i.Calculate service stress (fs) and Pt(% of tension steel) per the codal provisions given in Clause 26.5.1.7 of IS
fs = 0.58 fy(Ast reqd/Ast provide),Pt=100Ast/bd 456:2000.
ii.Find out modification factor (kt) for fs and Pt values i. The longitudinal reinforcement should be placed near
from IS code 456: 2000. to the periphery or corners of the beam section.
iii. (l/d)max =20xkt (for simply supported beams) ii. At least one longitudinal bar should be placed in each
(l/d)max=7xkt (for cantilever beams) corner of the section.
If (l/d)max > (l/d)provide ,hence ok iii. If the depth of the section exceeds 450 mm, additional
If (l/d)max < (l/d)provided,then redesign the section reinforcement in the form of bars should be provided
along the two side faces of the section, the area of side
Write the design procedure of RCC beam subjected face reinforcement should not be less than 0.1 % of the
to web area. This area should be distributed equally on both
equivalent shear force and equivalent bending the side faces at a spacing not less than 300 mm or
moment. breadth of the section.
A. Equivalent Shear Force (Ve): iv. In T and L beams, where the flanges are in tension,
1.Equivalent Shear Force is calculated as the torsional longitudinal reinforcement must be
Ve=Vu+1.6Tu/b distributed over the effective flange width or a width
2.Equivalent Nomial Shear Stress (𝜏ve) equal to one-tenth of the span, whichever is less. If the
The value of 𝜏ve should be less than 𝜏,cmax effective flange width exceeds one tenth of the span,
If 𝜏ve>𝜏cmax then the section is to be redesigned. minimum longitudinal reinforcement must be provided in
the outer portion of the flange
i. The shear strength of concrete (𝜏c) without
reinforcement is calculated and compare with 𝜏ve 2.Transverse Reinforcement:
ii. If 𝜏ve<𝜏c, then nominal shear reinforcement is i The transverse reinforcement is provided in the form of
provided in the form of stirrups such that closed links or hoops which enclose the longitudinal bars
provided along the corners or periphery of the beam
Asv/b.Sv)>/0.4/0.87fy section.
Sv</0.87fy.Asv/0.4b ii. The area of two legged closed hoops is given by:
Where,Asv = The cross sectional area of stirrup legs 0.87fy.(Asv/x)=(tu/bd1)+(Vu/2.5d1)
Fy= The characteristic strength of shear reinforcement But 0.87fy.(Asv/x)>/( 𝜏ve-𝜏c)b
b= The breadth of beam where x is the spacing of shear stirrups
Sv= The spacing of stirrups b1 and d1, is the centre to centre distance between corner
iii. If 𝜏ve>𝜏c i.e,, the equivalent nominal shear stress is bars in the direction of width and depth respectively as
greater than the shear strength of concrete, then torsional shown in Fig. 2.15.1.