QP 1 Jes

QP 1 Jeselyn
1. Fig. 1.1 shows the core of a transformer. It is made from thin sheets of iron.
(a) There are 200 sheets of iron in the core of the transformer. The thickness of the core is 50
mm. Calculate the average thickness of one sheet of iron
average thickness of one sheet = .................................................. mm [3]
(b) The density of the iron in the core is 7.65g/cm3. The mass of the core is 1377g. Calculate the
volume of the core.
volume = .................................................. cm3 [3]
(c) State the name of a device used to measure mass.

............................................................................................................................................. [1]
[Total: 7]
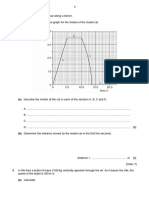
2. Fig. 2.1 shows how the speed of a car varies between 0 and 60.0s
final exam Page 1

(a) Determine the speed of the car using information from Fig. 2.1:
(i) when the time is 5.0s
speed = ................................................. m/s [2]
(ii) when the car is moving with a constant speed.
speed = ................................................. m/s [1]
(b) Describe how the speed of the car changes between 30.0s and 60.0s.
............................................................................................................................................. [2]
(c) Determine the distance travelled by the car between 10.0s and 30.0s.
distance travelled = ..................................................... m [3]
(d) The total distance travelled by the car in the last 30.0s is 226m.
Calculate the average speed of the car in the last 30.0s.
average speed = ................................................. m/s [3]

[Total: 11]
3. Fig. 3.1 shows a barrier used at a car park. The beam can be raised and lowered by a man rotating
it about its pivot.
final exam Page 2

(a) The weight of the beam is 150N. This acts at a distance of 1.8m from the pivot as shown in
Fig. 3.1.
Calculate the moment of the weight of the beam about the pivot.
Include the correct unit in your answer.
moment of weight of beam = ................................ unit ................. [4]
(b) When the weight W of the heavy weight acts at a distance of 0.6m from the pivot, the barrier
is horizontal and balanced as shown in Fig. 3.1.
The man raises the barrier and the heavy weight slips to a distance of 0.8m from the pivot.
This causes a problem for the man trying to lower the barrier.
Describe and explain the problem this causes for the man lowering the barrier.
...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
...................................................................................................................................................
............................................................................................................................................. [3]
[Total: 7]
4. A liquid-in-glass thermometer contains mercury.

(a) The mass of the mercury in the thermometer is 12g.
(i) Calculate the weight of the mercury.
weight of mercury = ..................................................... N [3]
(ii) The 12g of mercury has a volume of 0.88cm3.

Calculate the density of mercury.
density of mercury = .............................................. g/ cm3 [3]
(b) The mercury in the thermometer expands when its temperature rises.
(i) State what happens to the mass of the mercury when its temperature rises.
Tick (3) one box
(ii) State what happens to the density of the mercury when its temperature rises. Tick (3) one box
final exam Page 3

5. Fig. 2.1 shows a hammer being used to drive a nail into a piece of wood.
Fig. 2.1
The mass of the hammer head is 0.15 kg.
The speed of the hammer head when it hits the nail is 8.0 m / s.
The time for which the hammer head is in contact with the nail is 0.0015 s.
The hammer head stops after hitting the nail.
(a) Calculate the change in momentum of the hammer head.
change in momentum = ...........................................................[2]

(b) State the impulse given to the nail.
impulse = ...........................................................[1]
(c) Calculate the average force between the hammer and the nail.
average force = ...........................................................[2]

[Total: 5]
6. The engine of an unpowered toy train is rolling at a constant speed on a level track, as shown in
Fig. 3.1. The engine collides with a stationary toy truck, and joins with it.
Fig. 3.1
Before the collision, the toy engine is travelling at 0.32m/ s. The mass of the engine is 0.50kg.
(a) Calculate the momentum of the toy engine before the collision.
momentum = [2]
(b) The mass of the truck is 0.30kg.

Using the principle of conservation of momentum, calculate the speed of the joined engine
and truck immediately after the collision.
final exam Page 4

speed = [3]
[Total: 5]
7. (a) State Hooke’s law.

.......................................................................................................................................... ..................
................................................................................................................... [1]
(b) Fig. 1.1 shows a graph of the stretching force F acting on a spring against the extension x of
the spring.
(i) State the features of the graph that show that the spring obeys Hooke’s law.
.................................................................................................................................. ..........................
................................................................................................... [1]
(ii) Calculate k, the force per unit extension of the spring.
k = ...................................................[3]
iii) The limit of proportionality of the spring is reached at an extension of 50 mm. Continue the
graph in Fig. 1.1 to suggest how the spring behaves when the stretching force is increased to
values above 125 N. [1]
(iv) Another spring has a smaller value of k. This spring obeys Hooke’s law for extensions up to 80
mm. On the grid of Fig. 1.1, draw a possible line of the variation of F with x for this spring. [1]
[Total: 7]
final exam Page 5

QP 1 Jes

Uploaded by

Copyright:

Available Formats

QP 1 Jes

Uploaded by

Document Information

Original Title

Copyright

Available Formats

Share this document

Share or Embed Document

Sharing Options

Did you find this document useful?

Is this content inappropriate?

Copyright:

Available Formats

QP 1 Jes

Uploaded by

Copyright:

Available Formats

QP 1 Jeselyn

average thickness of one sheet = .................................................. mm [3]

volume = .................................................. cm3 [3]

(c) State the name of a device used to measure mass.

final exam Page 1

speed = ................................................. m/s [2]

(ii) when the car is moving with a constant speed.

speed = ................................................. m/s [1]

distance travelled = ..................................................... m [3]

average speed = ................................................. m/s [3]

final exam Page 2

moment of weight of beam = ................................ unit ................. [4]

4. A liquid-in-glass thermometer contains mercury.

weight of mercury = ..................................................... N [3]

(ii) The 12g of mercury has a volume of 0.88cm3.

density of mercury = .............................................. g/ cm3 [3]

final exam Page 3

change in momentum = ...........................................................[2]

average force = ...........................................................[2]

(b) The mass of the truck is 0.30kg.

final exam Page 4

7. (a) State Hooke’s law.

(ii) Calculate k, the force per unit extension of the spring.

final exam Page 5

You might also like