Air Leakage in Vacuum Vessels

Air Leakage in Vacuum Vessels
The chart, Fig. 1, is calculated from the formula: . 0.071*. p V ML = 0,071 * A t Where: MA = Air leakage in kg/h
p = Change of pressure in mbar p
t V
= Corresponding time in min Air leakage in kg/hr = Plant volume in m
How airtight is a vacuum plant? Is the suction capacity of the vacuum pump large enough? Why does it take so long for the plant to reach the vacuum? Must the vacuum pump extract leak air as well as gases from the product? Evacuate the vessel to a vacuum under 500 mbar, e. g. 60 mbar. Isolate the vacuum pump from the vessel and completely seal off the vessel. Measure the pressure increase in the vessel and determine the corresponding time. The pressure increase in mbar divided by the time in minutes gives the vacuum loss in mbar/minute. With this value and the volume of the vessel under vacuum the air leakage rate in kg/hr can be found in chart fig.1.
Vacuum loss in mbar/min

V= Plant volume
Fig 1
* the exact value is 0.071289977 based on: J universal gas constant = 8.31441 ,
mol K
absolute Temperature 293.15 K and mol mass for air 28.96 kg/kmol
Example: A vessel of 20 m volume is evacuated to 60 mbar and isolated. Within 10 minutes the vacuum drops to 120 mbar = p 60 mbar. The pressure change is 60 : 10 = 6 mbar/minute, therefore the vacuum loss is 6 mbar/minute. From the chart fig. 1 an air leakage rate of 8.5 kg/h is found.
In the high vacuum range the air leakage rate or the quantities of gases and vapours are measured in mbar litre/s. 1 mbar litre/s 0.0043 kg/hr air at 20 C
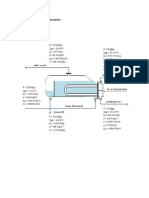
Admissible Velocity of Flow in Vacuum Pipelines

The admissible velocity of flow in a vacuum pipeline depends on how high the pressure loss of this pipeline is allowed to be. Higher pressure loss means increased energy requirements for the vacuum pump. A pressure loss of 10 % of the total pressure can generally be accepted. This is shown in graph fig. 1 and valid for air at 20 C. It is calculated according to the formula: wzul Wadm = wadm R 0.2 R T 0,2 . R . T . l 1 + 40 d = admissible velocity of flow in m/s = gas constant in J/kg K
R= r m
For reasons of simplication, the calculation is based on an average pipe friction coefficient of = 0.04 (this is ~ max.) and on a free-of-loss acceleration from 0 to w m/s, i. e. with a well rounded pipeline inlet. Range: 2 mbar p 1000 mbar. Furthermore the graph contains lines for constant volume flow V in m/hr. The graph is meant for rapid, rough dimensioning of a vacuum line. An exact pressure loss calculation can be made with the help of sheet 2000 abl 9.
r = 8314.3 J/kmol K= universal gas constant m = Mol mass in kg/kmol T I d = Temperature in K = Length of pipeline in m = Diameter of pipeline in mm
A 15
2000 abl 8
Admissible Velocity of Flow in Vacuum Pipelines
Admissible velocity of flow in m/s
p at p = 0.1 or 10%
Nominal diameter of pipeline in mm Fig 2

l= lenght of pipeline, V= volume flow
Example: calculation of mass flow Given: Pipeline ND 100 Length of pipeline I = 10 m Flow medium: Air at 20 C Total pressure p = 10 mbar Wanted: 1) Admissible velocity wadm in m/s 2) Volume flow V in m/hr 3) Mass flow M in kg/hr From the graph fig. 1 can be found: 1) wadm u 58m/s 2) V u 1650 m/hr Calculation: 3)
M= V kg/hr kg / h v
840 3 m / kg p vA = specific volume of air at 20C
vA = vL
If in the above example values for water vapour with a temperature = 7 C, p = 10 mbar and m = 18 kg/kmol are inserted, the following formula results: wadm = f wadm =
273 + 7 . 58 72 m / s . 18 10
p = pressure in mbar: . 1650 10 kg 20kg M= 840 Conversion to other gases and vapours If instead of air at 20 C another gas or vapour at the temperature in C is to be conveyed, the values from the graph have to be multiplied by the factor:
f= 273 + . m 10
from diagram fig. 2: Volume flow V u 2050 m/hr by calculation: Mass flow
M' = V' kg/hr kg / h v'
m = Mol mass of gas or vapours
from Water vapour temperature table zu = 7C; v = 129.1 m/kg therefore: 2050 M' = 16 kg / h kg/hr 129.1 129,1
Equivalent length of pipeline of pipe bends and gate valves are installed in the pipeline
I = I + e d . 40
Example Given are: Pipeline DN 600 Length of pipeline l = 100 m Flowing medium: air at 20C Total pressure p = 10 mbar 4 pipe bends 90; 1 gate valve Wanted: 1) Equivalent length of pipeline Ie in m 2) Admissible velocity of flow wadm in m/s 3) Volume flow V in m/hr 4) Mass flow in M kg/hr
By calculation we find: 1) 600 . . Ie = 100 + (4 0,16 + 1) 40 = 124.6 m From graph fig. 2 we find: 2) wadm u 44 m/s 3) V Hence: 4)
M=
Ie I d
= equivalent length of pipeline in m = length of pipeline in m = diameter of pipeline in mm = resistance coefficients: pipe bend D/d = 3; 90 = 0.16 gate valve with restriction = 1.0
u 45000 m/hr
45000 . 10 u kg / h kg/hr 535 535 840
A 16

Air Leakage in Vacuum Vessels

Uploaded by

Copyright:

Available Formats

Air Leakage in Vacuum Vessels

Uploaded by

Document Information

Copyright

Available Formats

Share this document

Share or Embed Document

Sharing Options

Did you find this document useful?

Is this content inappropriate?

Copyright:

Available Formats

Air Leakage in Vacuum Vessels

Uploaded by

Copyright:

Available Formats

Air Leakage in Vacuum Vessels

= Corresponding time in min Air leakage in kg/hr = Plant volume in m

Vacuum loss in mbar/min

Admissible Velocity of Flow in Vacuum Pipelines

Admissible Velocity of Flow in Vacuum Pipelines

Admissible velocity of flow in m/s

Nominal diameter of pipeline in mm Fig 2

840 3 m / kg p vA = specific volume of air at 20C

m = Mol mass of gas or vapours

45000 . 10 u kg / h kg/hr 535 535 840

You might also like