Location via proxy:   [ UP ]  
[Report a bug]   [Manage cookies]                
Scribd
Upload
2 views

Functions_3_and__-pages-3

The document outlines a mathematics study guide focused on power functions, including their properties such as being even or odd, symmetry, and behavior over domains. It includes tasks for sketching graphs, identifying intervals of increase or decrease, and exploring inverses of power functions. Additionally, it provides exercises related to inscribed rectangles in geometric shapes, emphasizing the calculation of areas and dimensions.

Uploaded by

Anujan
Copyright
© © All Rights Reserved
Available Formats
Download as PDF, TXT or read online on Scribd
2 views

Functions_3_and__-pages-3

The document outlines a mathematics study guide focused on power functions, including their properties such as being even or odd, symmetry, and behavior over domains. It includes tasks for sketching graphs, identifying intervals of increase or decrease, and exploring inverses of power functions. Additionally, it provides exercises related to inscribed rectangles in geometric shapes, emphasizing the calculation of areas and dimensions.

Uploaded by

Anujan
Copyright
© © All Rights Reserved
Available Formats
Download as PDF, TXT or read online on Scribd
You are on page 1/ 6

Mathematics

1G Power functions (Self study/Homework)


Learning intentions:
To investigate the properties of key power functions whether they are:

1. even or odd functions

2. symmetrical about the y-axis or about the origin

3. increasing or decreasing over a domain

4. the key points that they pass through

The concepts of strictly increasing and decreasing functions (Extracted


from VCAA/BULLETIN No. 87 April 2011)

Key points:

1. Strictly increasing : A function f (x) is said to be strictly increasing when a < b


implies f (a) < f (b) for all a and b in its domain.

2. Strictly decreasing
A function f (x) is said to be strictly decreasing when a < b implies f (a) > f (b) for
all a and b in its domain.

3. f (x) does not need to be differentiable, or to have a non-zero derivative


for it to be strictly increasing or decreasing

1. The piecewise function g has rule:


(
(x − 1)2 + 2 0 ≤ x ≤ 2
g(x) =
2x − 1 x>2

a. Sketch its graph on the grid


y

b. State the value/s of x for which the function g is strictly increasing.

Anandakumar Arulanantham Anujan Page 11


Mathematics

c. State the value/s of x for which the function g is not differentiable.

2. The function y = f (x) is shown to the right. For what values of x is f (x):

a. strictly decreasing?

b. strictly increasing?

3. The graph of the function f (x) is shown. For what values of x is the function
y = f (x) strictly decreasing?

A. (−3, 0) ∪ (0, ∞)
B. (−3, 0)
C. (−3, 0]
D. [−3, ∞)
E. (0, ∞)

Anandakumar Arulanantham Anujan Page 12


Mathematics

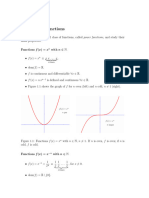
Part 2. Power functions with positive integer indices such as:

f (x) = x, f (x) = x2 , f (x) = x3 , f (x) = x4 , . . .

1. Sketch the graphs of f (x) = x, f (x) = x2 , f (x) = x3 , f (x) = x4 on the same set of
axes. Clearly mark the key points of intersections with coordinates.

2. Fill in the following table by observing the graphs you have drawn above.

When n is an When n
odd positive in- is an even
teger positive
integer
Odd or even function?
Over what interval(s) is the function strictly in-
creasing or decreasing?
One-to-one?
Key point(s) the graphs pass through?

Part 3. Power functions with negative integer indices such as:

f (x) = x−1 , f (x) = x−2 , f (x) = x−3 , f (x) = x−4 , . . .

a. Sketch the graphs on the same set of axes. Clearly mark the key points.

b. Fill in the following table:

Anandakumar Arulanantham Anujan Page 13


Mathematics

When n is an odd neg- When n is an even


ative integer negative integer
Odd or even function?
Domain
Range
Horizontal asymptote
Vertical asymptote

1
Part 4. The function f (x) = x n , where n is a positive integer, such as:
1 1 1
f (x) = x 2 , f (x) = x 3 , f (x) = x 4 , . . .
1 1 1
1. Sketch the graphs of f (x) = x 2 , f (x) = x 3 , f (x) = x 4 on the same set of axes.
Clearly mark the key points of intersections with coordinates.

2. Fill in the following table by observing the graphs you have drawn above.

When n is an odd posi- When n is an even posi-


tive integer tive integer
Domain

Over what interval(s)


is the function strictly
increasing or decreas-
ing?
One-to-one?

Key point(s) the


graphs pass through?

Anandakumar Arulanantham Anujan Page 14


Mathematics

Part 5. Inverses of Power Functions


1. If n is an odd positive integer, then f (x) = xn is strictly increasing for x ∈ R.
2. If f is an odd one-to-one function, then its inverse f −1 (x) is also an odd function.
1. For f : R → R, where f (x) = x5 :
(a) Find the rule of its inverse function f −1 (x).

(b) Define the inverse function f −1 (x).

2. A rectangle is inscribed in a semi-circle with a radius of 10 cm. The length of the


rectangle is 2x cm.

a. Write its width in terms of x.

b. Write an equation for calculating the area, A, of the rectangle.

c. State the set of all suitable values of x given A > 0.

d. Sketch the graph of A, labeling all the key points with coordinates.
y

Anandakumar Arulanantham Anujan Page 15


Mathematics

e. Find the dimensions of the rectangle for which the area of the rectangle is
maximum and state the maximum area.

3. A rectangle is inscribed in an isosceles triangle with dimensions as shown.

a. Express the width of the rectangle, y, in terms of x.

b. Write the area, A, of the rectangle in terms of x.

c. State the domain of A(x) given A > 0.

d. Sketch the graph of the area, labeling the key points as coordinates.
y

Anandakumar Arulanantham Anujan Page 16

You might also like