D PHYSICS

CSIR-NET, GATE, SET, JEST, IIT-JAM, BARC, TIFR

Contact: 8830156303 | 9860608078

DAILY DOSE
Practice Problem Series

Solid State Physics

PHYSICAL SCIENCE

DPHYSICS KRISHNA CHOWK, NEW SANGAVI, PUNE-27 CONTACT: 8830156303

[Date]
1. The first order diffraction peak of a crystalline solid occurs at a scattering angle of 30∘
when the diffraction pattern is recorded using an 𝑥-ray beam of wavelength 0.15 nm.
If the error in measurements of the wavelength and the angle are 0.01 nm and 1∘
respectively, then the error in calculating the inter-planar spacing will approximately
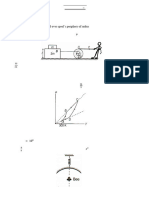
be
(a) 1.1 × 10−2 nm (b) 1.3 × 10−4 nm

(c) 2.5 × 10−2 nm (d) 2.0 × 10−3 nm

2. Potassium chloride forms an FCC lattice, in which 𝐾 and 𝐶𝑙 occupy alternating sites.
The density of 𝐾𝐶𝑙 is 1.98 g/cm3 and the atomic weights of 𝐾 and 𝐶𝑙 are 39.1 and 35.5,
respectively. The angles of incidence (in degrees) for which Bragg peaks will appear
when 𝑋-ray of wavelength 0.4 nm is shone on a KCl crystal are
(a) 18.5,39.4 and 72.2 (b) 19.5 and 41.9

(c) 12.5,25.7,40.5 and 60.0 (d)13.5,27.8,44.5 and 69.0

3. A narrow beam of electrons, accelerated under a potential difference, incident on a

crystal whose grating space is 0.3 nm. If the first diffraction ring is produced at an
angle 5.8∘ from the incident beam, find the momentum of the electrons and the
potential difference applied.

4. The Miller indices of a plane passing through the three points having coordinates
1 1 1
(0,0,1), (1,0,0), ( , , )
2 2 4
are
(a) (212) (b) (111) (c) (121) (d) (211)

5. In an 𝑋-Ray diffraction experiment on a solid with 𝐹𝐶𝐶 structure, five diffraction peaks
corresponding to (111), (200), (220), (311) and (222) planes are observed using
∘
1.54Å𝑋 rays. On using 3Å∘ 𝑋-rays on the same solid, the number of observed peaks will
be

DPHYSICS KRISHNA CHOWK, NEW SANGAVI, PUNE-27 CONTACT: 8830156303

6. The X-ray diffraction pattern of a monatomic cubic crystal with rigid spherical atoms of
radius 1.56£ shows several Bragg reflections of which the reflection appearing at the
lowest 2𝜃 value in from (111) plane. If the wavelength of X -ray used is 0.78Å, Bragg
angle (in 2𝜃, rounded off to one decimal place) corresponding to this reflection and the
crystal structure, respectively, are
(a) 21.6∘ and body centered cubic (b) 17.6∘ and face centered cubic

(c) 10.8∘ and body centered cubic (d) 8.8∘ and face centered cubic

7. The figure below shows the Bragg diffraction pattern for X-rays of wavelength 1.54Å
incident on two crystalline Silicon thin film Samples A and B. The dashed line
corresponds to a normal Sample A and the continuous line corresponds to another
Sample B, which is modified due to differences in the growth conditions.

These plots suggest that the modified sample 𝐵 is

(a) stretched in all directions by 3%

(b) compressed in all directions by 3%

(c) stretched in the 𝑧 direction by 1% and possibly compressed in 𝑥&𝑦 directions

(d) compressed in the 𝑧 direction by 1% and possibly stretched out in 𝑥&𝑦 directions

DPHYSICS KRISHNA CHOWK, NEW SANGAVI, PUNE-27 CONTACT: 8830156303

8. The pictures below are intended to denote a two-dimensional lattice with primitive
vectors indicated by arrows and with the unit cell shaded. Which of the following
pictures is correct?

9. An X-ray of wavelength 𝜆, when incident on the (101) plane of a cubic lattice with
lattice constant 𝑎 produces a first-order Bragg's reflection at 𝜃 = 30∘ (𝜃 is measured
from the lattice plane).
Suppose this cubic lattice is compressed along the 𝑧 axis such that its lattice
parameters along the 𝑥 and 𝑦 axes remain the same while that along the 𝑧 axis becomes
1
𝑎 (see figure).
√3

DPHYSICS KRISHNA CHOWK, NEW SANGAVI, PUNE-27 CONTACT: 8830156303

 The first-order reflection for the (101) plane of the compressed lattice occurs at:
(a) 𝜃 = 60∘ (b) 𝜃 = 15∘ (c) 𝜃 = 30∘ (d) 𝜃 = 45∘

10. A one-dimensional linear chain of atoms contains two types of atoms of masses 𝑚1 and
𝑚2 (where 𝑚2 > 𝑚1 ), arranged alternately. The distance between successive atoms is
the same. Assume that the harmonic approximation is valid. At the first Brillouin zone
boundary, which of the following statement is correct?

(a) The atoms of mass 𝑚2 are at rest in the optical mode, while they vibrate in the
acoustical mod

(b) The atoms of mass 𝑚1 are at rest in the optical mode, while they vibrate in the
acoustical mode

(c) Both types of atoms vibrate with equal amplitudes in the optical as well as in the
acoustical modes

(d) Both types of atoms vibrate, but with unequal non-zero amplitudes in the optical as
well as in the acoustical modes

𝜔𝐷
11. The total number of phonon modes in a solid of volume 𝑉 is ∫0 𝑔(𝜔)𝑑𝜔 = 3𝑁, where
𝑁 is the number of primitive cells, 𝜔3 is the Debye frequency and density of photon
modes is 𝑔(𝜔) = 𝐴𝑉𝜔2 (with 𝐴 > 0 a constant). If the density of the solid doubles in a
phase transition, the Debye temperature 𝜃𝐷 will
(a) increase by a factor of 22/3 (b) increase by a factor of 21/3

(c) decrease by a factor of 22/3 (d) decrease by a factor of 21/3

12. Consider a one-dimensional chain of atoms with lattice constant 𝑎. The energy of an
electron with wave-vector 𝑘 is 𝜀(𝑘) = 𝜇 − 𝛾cos (𝑘𝑎), where 𝜇 and 𝛾 are constants. If an
electric field 𝐸 is applied in the positive 𝑥-direction, the time dependent velocity of an
electron is (in the following 𝐵 is the constant)

DPHYSICS KRISHNA CHOWK, NEW SANGAVI, PUNE-27 CONTACT: 8830156303

 𝑒𝐸
(a) proportional tocos (𝐵 − 𝑎𝑡) (b) proportional to 𝐸
ℏ

𝑒𝐸
(c) independent of𝐸 (d) proportional tosin (𝐵 − 𝑎𝑡)
ℏ

13. The Fermi energies of two metals X and Y are 5eV and 7eV and their Debye
temperatures are 170 K and 340 K. respectively. The molar specific heats of theses
metals at constant volume at low temperature can be written as (𝐶𝑉 )𝑥 = 𝛾𝑥 𝑇 + 𝐴𝑥 𝑇 3
and (𝐶𝑉 )𝑦 = 𝛾𝛾 𝑇 + 𝐴𝑦 𝑇 3 , where 𝛾 and A are constants. Assuming that the thermal
effective mass of the electrons in the two metals are same which of the following is
correct?
𝛾𝑥 7 𝐴𝑥 𝛾𝑥 7 𝐴𝑥 1
(a) = , =8 (b) = , =
𝛾𝑦 5 𝐴𝑦 𝛾𝑦 5 𝐴𝑦 8

𝛾𝑥 5 𝐴𝑥 1 𝛾𝑥 5 𝐴𝑥
(c) = , = (d) = , =8
𝛾𝑦 7 𝐴𝑦 8 𝛾𝑦 7 𝐴𝑦

14. A particle of mass 𝑚 moves in a lattice along the 𝑥-axis in a periodic potential 𝑉(𝑥) =
𝑉(𝑥 + 𝑑) with periodicity 𝑑. The corresponding Brillouin zone extends from −𝑘0 to 𝑘0
with these two 𝑘-points being equivalent. If a weak force 𝐹 in the 𝑥-direction is applied
to the particle, it starts a periodic motion with time period 𝑇. Using the equation of
motion
𝑑𝑝crystal
𝐹=
𝑑𝑡
for a particle moving in a band, where 𝑝crystal is the crystal momentum of the particle,
the period 𝑇 is found to be ( ℎ is Planck constant)

2𝑚𝑑 2𝑚𝑑 2ℎ ℎ
(a)√ (b) 2√ (c) (d)
𝐹 𝐹 𝐹𝑑 𝐹𝑑

15. A particle is confined to a one-dimensional lattice with a lattice spacing 𝛿. In the

position space, the Hamiltonian operator for this particle is given by the matrix

DPHYSICS KRISHNA CHOWK, NEW SANGAVI, PUNE-27 CONTACT: 8830156303

 ⋱
… … 0 0 0 0
… 2 −1 0 0 0
ℋ = 𝐸0 0 −1 2 −1 0 0
0 0 −1 2 −1 0
0 0 0 −1 2 ⋯
0 0 0 0 ⋯ ⋯
( ⋱)
Noting that it commutes with the generator 𝑇 of translations
⋱
… … 0 0 0 0
… 0 1 0 0 0
𝒯= 0 0 0 1 0 0
0 0 0 0 1 0
0 0 0 0 0 …
0 0 0 0 … …
( ⋱)
where 𝑇 = 𝑒 𝑖𝒫𝛿/ℏ in terms of the momentum operator 𝒫, the energy of a state with
momentum 𝑝 will be
(a) 𝐸0 sin (𝑝𝛿/ℏ) (b) 𝐸0 cos (𝑝𝛿/ℏ) (c) 4𝐸0 sin2 (𝑝𝛿/2ℏ) (d) 𝐸0 (𝑝𝛿/2ℏ)2

16. An extrinsic semiconductor sample of cross-section 𝐴 and length 𝐿 is doped in such a

way that the doping concentration varies as
𝑥
𝑁𝐷 (𝑥) = 𝑁0 exp (− )
𝐿
where 𝑁0 is a constant. Assume that the mobility 𝜇 of the majority carriers remains
constant. The resistance 𝑅 of the sample is given by
𝐿 𝐿
(a)𝑅 = [exp (1.0) − 1] (b)𝑅 = [exp (1.0) − 1]
𝐴𝜇𝑒𝑁0 𝜇𝑒𝑁0

𝐿 𝐿
(c)𝑅 = [exp (−1.0) − 1] (d)𝑅 =
𝐴𝜇𝑒𝑁0 𝐴𝜇𝑒𝑁0

17. A thin rectangular conducting plate of length 𝑎 and width 𝑏 is placed in the 𝑥𝑦-plane in
two different orientations, as shown in the figures below. In both cases a magnetic field
𝐵 is applied in the 𝑧 direction and a current flow in the 𝑥-direction due to the applied

DPHYSICS KRISHNA CHOWK, NEW SANGAVI, PUNE-27 CONTACT: 8830156303

 voltage 𝑉.

If the Hall voltage across the 𝑦-direction in the two cases satisfy 𝑉2 = 2𝑉1, the ratio 𝑎: 𝑏
must be
(a) 1: 2 (b) 1: √2 (c) 2: 1 (d) √2: 1

18. The Hall co-efficient for a semiconductor having both types of carriers is given as:
𝑝𝜇𝑝2 − 𝑛𝜇𝑛2
𝑅𝐻 = 2
|𝑒|(𝑝𝜇𝑝 + 𝑛𝜇𝑛 )
where 𝑝 and 𝑛 are the carrier densities of the holes and electrons, 𝜇𝑝 and 𝜇𝑛 are their
respective mobilities. For a p-type semiconductor in which the mobility of holes is less
than that of electrons, which of the following graphs best describes the variation of the
Hall coefficient with temperature?

DPHYSICS KRISHNA CHOWK, NEW SANGAVI, PUNE-27 CONTACT: 8830156303

 19. A 𝑝 - doped semiconductor slab carries a current 𝐼 = 100 mA in a magnetic field 𝐵 =
0.2𝑇 as shown. One measures 𝑉𝑦 = 0.25mV and 𝑉𝑥 = 2mV. The mobility of holes in the
semiconductor is 𝑚2 𝑉 −1 𝑠 −1 (up to two decimal places)

20. An extrinsic semiconductor shown in figure carries a current of 2 mA along its length
parallel to +𝑥 axis. When the majority charge carrier concentration is 12.5 × 1013 cm−3
and the sample is exposed to a constant magnetic field applied along the +𝑧 direction, a
Hall voltage of 20 mV is measured with the negative polarity at 𝑦 = 0

plane. Take the electric charge as 1.6 × 10−19 C. The concentration of minority charge
carrier is negligible. Which of the following statement is/are true?
(a) The majority charge carrier is electron

(b) The magnitude of the applied magnetic field is 1 Tesla

(c) The electric field corresponding to the Hall voltage is in the +𝑦 direction

(d) The magnitude of Hall coefficient is 50,000 m3 C−1

Answer Key
1. a 2. a 3. 3.67Kv 4. a 5. 1 6. b 7. d 8. a 9. d 10. a
11. b 12. d 13. a 14. d 15. c 16. b 17. d 18. d 19. 1.55 20. ab

DPHYSICS KRISHNA CHOWK, NEW SANGAVI, PUNE-27 CONTACT: 8830156303

 📌Get full CSIR NET/JRF 6 March 2025 LIVE BATCH (6/12 Month) Course from

D Physics .👉Course Link:- https://dphysics.akamai.net.in/new-courses/186

📌Get full MH-SET live Crash Course 10 March 2025 Course from D Physics
👉Course Link:- https://dphysics.akamai.net.in/new-courses/190

DPHYSICS KRISHNA CHOWK, NEW SANGAVI, PUNE-27 CONTACT: 8830156303