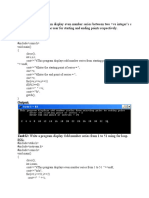
0 ratings0% found this document useful (0 votes)
157 viewsGaddis Python 4e Chapter 12
Uploaded by
JM MejiaCopyright
© © All Rights Reserved
Available Formats
Download as PPT, PDF, TXT or read online on Scribd
0 ratings0% found this document useful (0 votes)
157 viewsGaddis Python 4e Chapter 12
Uploaded by
JM MejiaCopyright
© © All Rights Reserved
Available Formats
Download as PPT, PDF, TXT or read online on Scribd
You are on page 1/ 23
C H A P T E R 12
Recursion
Copyright © 2018 Pearson Education, Inc.
Topics
• Introduction to Recursion
• Problem Solving with Recursion
• Examples of Recursive Algorithms
Copyright © 2018 Pearson Education, Inc.
Introduction to Recursion
• Recursive function: a function that calls
itself
• Recursive function must have a way to
control the number of times it repeats
• Usually involves an if-else statement which
defines when the function should return a value
and when it should call itself
• Depth of recursion: the number of times
a function calls itself
Copyright © 2018 Pearson Education, Inc.
Copyright © 2018 Pearson Education, Inc.
Introduction to Recursion
(cont’d.)
Copyright © 2018 Pearson Education, Inc.
Problem Solving with
Recursion
• Recursion is a powerful tool for solving
repetitive problems
• Recursion is never required to solve a
problem
• Any problem that can be solved recursively
can be solved with a loop
• Recursive algorithms usually less efficient
than iterative ones
• Due to overhead of each function call
Copyright © 2018 Pearson Education, Inc.
Problem Solving with
Recursion (cont’d.)
• Some repetitive problems are more easily
solved with recursion
• General outline of recursive function:
• If the problem can be solved now without
recursion, solve and return
• Known as the base case
• Otherwise, reduce problem to smaller problem of
the same structure and call the function again to
solve the smaller problem
• Known as the recursive case
Copyright © 2018 Pearson Education, Inc.
Using Recursion to Calculate
the Factorial of a Number
• In mathematics, the n! notation
represents the factorial of a number n
• For n = 0, n! = 1
• For n > 0, n! = 1 x 2 x 3 x … x n
• The above definition lends itself to
recursive programming
• n = 0 is the base case
• n > 0 is the recursive case
• factorial(n) = n x factorial(n-1)
Copyright © 2018 Pearson Education, Inc.
Using Recursion (cont’d.)
Copyright © 2018 Pearson Education, Inc.
Copyright © 2018 Pearson Education, Inc.
Using Recursion (cont’d.)
• Since each call to the recursive
function reduces the problem:
• Eventually, it will get to the base case which
does not require recursion, and the recursion
will stop
• Usually the problem is reduced by
making one or more parameters
smaller at each function call
Copyright © 2018 Pearson Education, Inc.
Direct and Indirect Recursion
• Direct recursion: when a function
directly calls itself
• All the examples shown so far were of direct
recursion
• Indirect recursion: when function A
calls function B, which in turn calls
function A
Copyright © 2018 Pearson Education, Inc.
Examples of Recursive
Algorithms
• Summing a range of list elements with
recursion
• Function receives a list containing range of
elements to be summed, index of starting item
in the range, and index of ending item in the
range
• Base case:
• if start index > end index return 0
• Recursive case:
• return current_number + sum(list, start+1, end)
Copyright © 2018 Pearson Education, Inc.
Examples of Recursive
Algorithms (cont’d.)
Copyright © 2018 Pearson Education, Inc.
The Fibonacci Series
• Fibonacci series: has two base cases
• if n = 0 then Fib(n) = 0
• if n = 1 then Fib(n) = 1
• if n > 1 then Fib(n) = Fib(n-1) + Fib(n-2)
• Corresponding function code:
Copyright © 2018 Pearson Education, Inc.
Finding the Greatest Common
Divisor
• Calculation of the greatest common divisor (GCD) of
two positive integers
• If x can be evenly divided by y, then
• gcd(x,y) = y
• Otherwise, gcd(x,y) = gcd(y, remainder of x/y)
• Corresponding function code:
Copyright © 2018 Pearson Education, Inc.
The Towers of Hanoi
• Mathematical game commonly used to
illustrate the power of recursion
• Uses three pegs and a set of discs in
decreasing sizes
• Goal of the game: move the discs from leftmost
peg to rightmost peg
• Only one disc can be moved at a time
• A disc cannot be placed on top of a smaller disc
• All discs must be on a peg except while being
moved
Copyright © 2018 Pearson Education, Inc.
The Towers of Hanoi (cont’d.)
Copyright © 2018 Pearson Education, Inc.
Copyright © 2018 Pearson Education, Inc.
The Towers of Hanoi (cont’d)
• Problem statement: move n discs from
peg 1 to peg 3 using peg 2 as a
temporary peg
• Recursive solution:
• If n == 1: Move disc from peg 1 to peg 3
• Otherwise:
• Move n-1 discs from peg 1 to peg 2, using peg 3
• Move remaining disc from peg 1 to peg 3
• Move n-1 discs from peg 2 to peg 3, using peg 1
Copyright © 2018 Pearson Education, Inc.
The Towers of Hanoi (cont’d.)
Copyright © 2018 Pearson Education, Inc.
Recursion versus Looping
• Reasons not to use recursion:
• Less efficient: entails function calling
overhead that is not necessary with a loop
• Usually a solution using a loop is more
evident than a recursive solution
• Some problems are more easily solved
with recursion than with a loop
• Example: Fibonacci, where the mathematical
definition lends itself to recursion
Copyright © 2018 Pearson Education, Inc.
Summary
• This chapter covered:
• Definition of recursion
• The importance of the base case
• The recursive case as reducing the problem
size
• Direct and indirect recursion
• Examples of recursive algorithms
• Recursion versus looping
Copyright © 2018 Pearson Education, Inc.
You might also like
- Python 4e - Answers To Review QuestionsNo ratings yetPython 4e - Answers To Review Questions31 pages
- Starting Out With Programming Logic & Design - Chapter13 - RecursionNo ratings yetStarting Out With Programming Logic & Design - Chapter13 - Recursion19 pages
- 03 - Gaddis Python - Lecture - PPT - ch03No ratings yet03 - Gaddis Python - Lecture - PPT - ch0339 pages
- Addition Means - These Are The Steps On How To Do Addition Within 100No ratings yetAddition Means - These Are The Steps On How To Do Addition Within 1004 pages
- 01 - Gaddis Python - Lecture - PPT - ch01No ratings yet01 - Gaddis Python - Lecture - PPT - ch0130 pages
- 06 - Gaddis Python - Lecture - PPT - ch06No ratings yet06 - Gaddis Python - Lecture - PPT - ch0630 pages
- Gaddis Python 6e Chapter 03 - AccessibleNo ratings yetGaddis Python 6e Chapter 03 - Accessible49 pages
- Dictionaries Tuples Assignment For PythonNo ratings yetDictionaries Tuples Assignment For Python5 pages
- 08 - Gaddis Python - Lecture - PPT - ch08No ratings yet08 - Gaddis Python - Lecture - PPT - ch0821 pages
- Object Oriented Programming (OOP) - CS304 Power Point Slides Lecture 21No ratings yetObject Oriented Programming (OOP) - CS304 Power Point Slides Lecture 2149 pages
- Algorithms: 2006 S. Dasgupta, C. H. Papadimitriou, and U. V. Vazirani July 18, 2006No ratings yetAlgorithms: 2006 S. Dasgupta, C. H. Papadimitriou, and U. V. Vazirani July 18, 20068 pages
- Object Oriented Programming (OOP) - CS304 Power Point Slides Lecture 40No ratings yetObject Oriented Programming (OOP) - CS304 Power Point Slides Lecture 4031 pages
- 04 - Gaddis Python - Lecture - PPT - ch04No ratings yet04 - Gaddis Python - Lecture - PPT - ch0430 pages
- Object Oriented Programming (OOP) - CS304 Power Point Slides Lecture 02No ratings yetObject Oriented Programming (OOP) - CS304 Power Point Slides Lecture 0221 pages
- National High School Programming Contest 2020 - Practice ContestNo ratings yetNational High School Programming Contest 2020 - Practice Contest25 pages
- (C++ Examples) 51 TO 108 PROGRAME (EE01083101)No ratings yet(C++ Examples) 51 TO 108 PROGRAME (EE01083101)54 pages
- Object Oriented Programming (OOP) - CS304 Power Point Slides Lecture 42No ratings yetObject Oriented Programming (OOP) - CS304 Power Point Slides Lecture 4243 pages
- Our Shrinking World: Computers & The Global EconomyNo ratings yetOur Shrinking World: Computers & The Global Economy25 pages
- Midterm Faqs: - We Are Strict When Grading The SyntaxNo ratings yetMidterm Faqs: - We Are Strict When Grading The Syntax4 pages
- Special Pairs of Rectangles and Sphenic NumberNo ratings yetSpecial Pairs of Rectangles and Sphenic Number3 pages
- 320 - CS8391 Data Structures - Important Questions100% (5)320 - CS8391 Data Structures - Important Questions22 pages
- Arunai Theory Exam Time Table NovDec2024No ratings yetArunai Theory Exam Time Table NovDec202425 pages
- Cracking The Coding Interview 6th Edition PDF0% (1)Cracking The Coding Interview 6th Edition PDF4 pages
- 3D Tic Tac Toe: Board State RepresentationNo ratings yet3D Tic Tac Toe: Board State Representation5 pages
- 8 - Class INTSO Work Sheet - 3 - Square Roorts and Cube RootsNo ratings yet8 - Class INTSO Work Sheet - 3 - Square Roorts and Cube Roots2 pages
- Imp Notes For Final Term by Daniyal Subhani Cs502 Important Question With Answer PreparedNo ratings yetImp Notes For Final Term by Daniyal Subhani Cs502 Important Question With Answer Prepared9 pages
- Starting Out With Programming Logic & Design - Chapter13 - RecursionStarting Out With Programming Logic & Design - Chapter13 - Recursion
- Addition Means - These Are The Steps On How To Do Addition Within 100Addition Means - These Are The Steps On How To Do Addition Within 100
- Object Oriented Programming (OOP) - CS304 Power Point Slides Lecture 21Object Oriented Programming (OOP) - CS304 Power Point Slides Lecture 21
- Algorithms: 2006 S. Dasgupta, C. H. Papadimitriou, and U. V. Vazirani July 18, 2006Algorithms: 2006 S. Dasgupta, C. H. Papadimitriou, and U. V. Vazirani July 18, 2006
- Object Oriented Programming (OOP) - CS304 Power Point Slides Lecture 40Object Oriented Programming (OOP) - CS304 Power Point Slides Lecture 40
- Object Oriented Programming (OOP) - CS304 Power Point Slides Lecture 02Object Oriented Programming (OOP) - CS304 Power Point Slides Lecture 02
- National High School Programming Contest 2020 - Practice ContestNational High School Programming Contest 2020 - Practice Contest
- Object Oriented Programming (OOP) - CS304 Power Point Slides Lecture 42Object Oriented Programming (OOP) - CS304 Power Point Slides Lecture 42
- Our Shrinking World: Computers & The Global EconomyOur Shrinking World: Computers & The Global Economy
- Midterm Faqs: - We Are Strict When Grading The SyntaxMidterm Faqs: - We Are Strict When Grading The Syntax
- 320 - CS8391 Data Structures - Important Questions320 - CS8391 Data Structures - Important Questions
- 8 - Class INTSO Work Sheet - 3 - Square Roorts and Cube Roots8 - Class INTSO Work Sheet - 3 - Square Roorts and Cube Roots
- Imp Notes For Final Term by Daniyal Subhani Cs502 Important Question With Answer PreparedImp Notes For Final Term by Daniyal Subhani Cs502 Important Question With Answer Prepared