Introduction to basic statistics

Introduction to Basic Statistics

Pat Hammett, Ph.D.

2005

Instructor Comments:

This document contains an overview of basic probability and statistics. It
also includes a practice test at the end of the document. Note: answers to
the practice test questions are included in an appendix.

1

Pat Hammett University of Michigan

Table of Contents

1. VARIABLES- QUALITATIVE AND QUANTITATIVE......................3
1.1 Qualitative Data (Categorical Variables or Attributes) ........................... 3
1.2 Quantitative Data............................................................................................... 4
2. DESCRIPTIVE STATISTICS.................................................6
2.1 Sample Data versus Population Data ................................................................... 6
2.2 Parameters and Statistics..................................................................................... 6
2.3 Location Statistics (measures of central tendency) ...................................... 7
2.4 Dispersion Statistics (measures of variability) ............................................... 8
3. FREQUENCY DISTRIBUTIONS ........................................... 10
3.1 Frequency Measures.............................................................................................. 10
3.2 Histogram .................................................................................................................11
3.3 Discrete Histogram............................................................................................... 12
3.4 Continuous Data Histogram ................................................................................. 13
4. NORMAL DISTRIBUTION ................................................. 15
4.1 Properties of the Normal Distribution ............................................................. 15
4.2 Estimating Probabilities Using Normal Distribution ..................................... 16
4.3 Calculating Parts Per Million Defects Given Normal Distribution.............. 17
5. LINEAR REGRESSION ANALYSIS ........................................ 20
5.1 General Regression equation............................................................................... 20
5.2 Simple linear regression...................................................................................... 20
5.3 Correlation.............................................................................................................. 22
5.4 Using Scatter Plots to Show Linear Relationships ....................................... 23
5.5 Multiple linear regression................................................................................... 24

Appendices:
A – Practice Test
B – Normal Distribution Tables
C – Useful Excel Functions

2


1. VARIABLES- QUALITATIVE AND QUANTITATIVE

A variable is any measured characteristic or attribute that differs for
different subjects. For example, if the length of 30 desks were measured, then
length would be a variable.

Key Learning Skills –
• Understand the difference between a qualitative (categorical) variable
and a quantitative variable.
• Understand the types of qualitative (categorical) variables: Nominal,
Ordinal, and Binary.
• Understand the difference between a discrete and a continuous
quantitative variable.

Terms and Definitions:

1.1 Qualitative Data (Categorical Variables or Attributes)

Qualitative data involves assigning non-numerical items into groups or
categories. Qualitative data also are referred to as categorical data. The
qualitative characteristic or classification group of an item is an attribute.
Some examples of qualitative data are:
• The pizza was delivered on time.
• Categorical Variable: Delivery Result
• Attribute: On Time, Not On Time
• The survey responses include disagree, neutral, or agree.
• Categorical Variable: Survey Response
• Attribute: Disagree, Neutral, Agree
• This car comes in black, white, red, blue, or yellow.
• Categorical Variable: Color
• Attribute: Black, White, Red, Blue, or Yellow.

Categorical variables are typically assigned attributes using a nominal,
ordinal, or binary scale.
• Nominal variables are categorical variables that have three or
more possible levels with no natural ordering. Car color would be
considered a nominal variable. Again, in a nominal scale, no

3


quantitative information is conveyed and no ordering of the items
is implied. Other examples of nominal scales include religious
preference, production facility, and organizational function.
• Ordinal variables are categorical variables that have three or more
possible levels with a natural ordering, such as strongly disagree,
disagree, neutral, agree, and strongly agree. With ordinal data,
quality analysts often convert it to a quantitative scale. For
example, a survey may assign a scale from 1-5 to cover the range
from strongly disagree, to neutral, to strongly agree. When
converting an ordinal categorical variable to a quantitative scale, a
quality analyst must exercise caution in the interpretation of the
difference between values. For instance, the difference between
the responses strongly disagree (1) and disagree (2) may not equal
the difference between disagree (2) and neutral (3).
• Binary variables are categorical variables that have two possible
levels (e.g., yes/no). Binary variables are the most common type of
categorical variables because they are the easiest to convert to a
quantitative scale. Binary variables typically are assigned a 0 (e.g.,
defective) or 1 (e.g., not defective). This use of the 0 / 1
designation allows experimenters to use proportions or counts for
data analysis. As a general rule, the desired outcome is assigned
the 1.

1.2 Quantitative Data

Quantitative Data result from measurement or numerical estimation. These
measurements yield discrete or continuous variables. Discrete variables
vary only by whole numbers such as the number of students in a class
(variable: class size). Continuous variables vary to any degree, limited only by
the precision of the measurement system. Some examples include the width
of a desk, the time to complete a task, or the height of students (variables:
length, time, and height). In the case of measuring the width of a desk, the
measurement could read 1.54 m, or 1.541 m, or 1.5409, or 1.54087, ... Here,
the observed measurement is limited only by the precision of the
measurement instrument.

4


Some additional examples of continuous quantitative measurements are:
• The time to deliver the pizza was 26.7 minutes.
• The diameter of the cylinder was 83.1 mm.

In converting a categorical variable to a quantitative scale, the variable is
typically treated as a discrete variable. For example, a rating scale from 1 to
5 or a binary scale of 0 or 1 would be analyzed as a discrete variable. In
computing a statistic for a discrete variable such as the average survey
response, the statistic (e.g., the average) is considered continuous. So, the
average for a 5-points scale might be 3.72 even though this particular value
is not possible to obtain.

For analysis purposes, discrete variables often are approximated using
continuous distributions. For instance, suppose student test scores are
discrete ranging from 0 to 100 points. Here, we might assume the
distribution of test scores follows a normal distribution (continuous) in order
to estimate the likelihood of a student scoring greater than a 70.

In general, analysts try to convert all data to an approximately continuous,
numerical scale for making inferences or conclusions.

5


2. DESCRIPTIVE STATISTICS

Descriptive statistics are used to summarize the characteristics of a data set.

• Understand the difference between a sample and a population.
• Understand the difference between a parameter and a statistic.
• Compute the mean, median, standard deviation, variance and the range
for a sample data set.


2.1 Sample Data versus Population Data

A population data set includes all items of the set, such as the height of
every person in the United States, or the volume of every can of soda pop
that a manufacturer produces. If the desired information is available for all
items in the population, we have what is referred to as a census. In practice,
we rarely have a complete set of data. We usually collect data in samples,
such as the volumes of the last thirty cans of pop.

2.2 Parameters and Statistics

Numbers used to describe a population are parameters and often are
denoted using Greek letters. Numbers used to describe a sample data set
are called statistics. A Statistic may be used to estimate a population
parameter such as the average of a data set ( X or µ ) provides an estimate
ˆ
of the population mean, µ.

The difference between a statistic and a parameter is important to
understand because in statistical data analysis we often make inferences
about a population based on sample statistics. Since we rarely know every
observation in a population, any conclusions or recommendations that are
made based on sample statistics are subject to error. However, we typically
will accept some margin of error rather than incur the cost of measuring
every observation.

6


2.3 Location Statistics (measures of central tendency)

Mean (also known as the average) is a measure of the center of a
distribution.

X 1 + X 2 + ... X N
Mean = Note : Mean is also referred to as X
N

The typical notation used to represent the mean of a sample of data is X ;
the Greek letter µ is used to represent the mean of a population. The terms,
X or µ , represent the estimate of the population mean.
ˆ

Example: suppose five students take a test and their scores are 70, 68, 71,
69 and 98.

Mean = (70+68+71+69+98)/5 = 75.2

Notice: the mean may be strongly influenced by extreme values. If we
excluded the student whose score was a 98, the mean would change to 69.5.

Median (also known as the 50th percentile) is the middle observation in a
data set. To determine the median, we rank the data set and then select the
middle value. If the data set has an odd number of observations, the middle
value is the observation number [N + 1] / 2. If the data set has an even
number of observations, the middle value is extrapolated as midway between
observation numbers N / 2 and [N / 2] + 1.

In the above example, the data ranked is 68, 69, 70, 71, and 98. Here, the
median is 70. If another student with a score of 60 was included, the new
median would 69.5 (69 + 70 / 2).

The median is often used if the data has extreme values (outliers) or is
skewed (e.g., if one of the tails of a bell-shaped curve is significantly longer
than the other). In the above example of student test scores, the median
provides a better representation of the center of the distribution since 98
is an extreme value.

7


2.4 Dispersion Statistics (measures of variability)

Standard deviation (StDev) measures the dispersion of the individual
observations from the mean. In a sample data set, the standard deviation is
also referred to as the sample standard deviation or the root-mean-square
Srms and may be calculated using the following formula.

n

∑(X i − X )2
S= i =1
n −1

Note: to compute the population standard deviation, we use the population
mean and divide by n instead of n-1. In practice, the population standard
deviation is rarely used because the true population mean is usually unknown.
The use of the sample standard deviation is particularly important for
smaller sample sizes. However, as the sample size gets large (say n > 100),
the difference between dividing by n versus n-1 may become negligible.

The typical notation used to represent the sample standard deviation is S;
the Greek letter σ is used to represent the population standard deviation.
The terms, S or σ , represent the estimate of the population standard
ˆ
deviation.

In the example with the five student test scores (70, 68, 71, 69 and 98), the
sample standard deviation is 12.79.

Similar to the mean, the standard deviation may be strongly influenced by
extreme values. If we exclude the student whose score was a 98, the sample
standard deviation would be reduced to 1.3!

Variance is sometimes used to represent dispersion. The variance is simply
the standard deviation squared. The variance represents the average
squared deviation from the mean.

n

∑(X i − X )2
S2 = i =1
n −1

8


Above Example: Variance = (12.79)2 = 163.72

Note: the variance is often used because of its additive property. If several
independent factors contribute to the overall variance, then the total
variance may be determined by adding the individual factor variances
(assuming the factors are independent). Note: we do not add standard
deviations!

Range is another measure of dispersion. The range is simply the maximum
value in a data set minus the minimum value. In the above example, the range
of (70, 68, 71, 69 and 98) is (98 - 68 = 30).

Note: the range is sometime preferred over the standard deviation to
represent dispersion for small data sets (e.g., # of samples < 10).

9


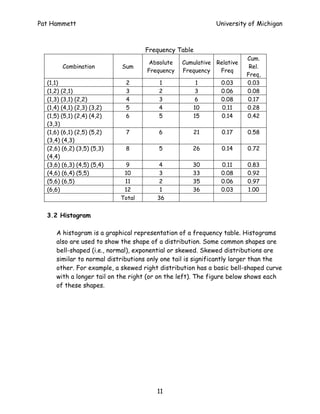
3. FREQUENCY DISTRIBUTIONS

Frequency is used to describe the number of times a value or a range of values
occurs in a data set. Cumulative frequencies are used to describe the number of
observations less than, or greater than a specific value.

• Understand the difference between absolute, relative, and cumulative
frequencies.
• Generate a frequency table.
• Generate a histogram.


3.1 Frequency Measures

Absolute frequency is the number of times a value or range of values occurs
in a data set. The relative frequency is found by dividing the absolute
frequency by the total number of observations (n). The cumulative frequency
is the successive sums of absolute frequencies. The cumulative relative
frequency is the successive sum of cumulative frequencies divided by the
total number of observations.

To demonstrate the differences between these terms, consider the results
of throwing a pair of dice. The possible combinations and their sums are
shown in the following frequency table. Four measures of frequency are
shown: absolute frequency, cumulative frequency, relative frequency, and
cumulative relative frequency.

10


Frequency Table
Cum.
Absolute Cumulative Relative
Combination Sum Rel.
Frequency Frequency Freq
Freq,
(1,1) 2 1 1 0.03 0.03
(1,2) (2,1) 3 2 3 0.06 0.08
(1,3) (3,1) (2,2) 4 3 6 0.08 0.17
(1,4) (4,1) (2,3) (3,2) 5 4 10 0.11 0.28
(1,5) (5,1) (2,4) (4,2) 6 5 15 0.14 0.42
(3,3)
(1,6) (6,1) (2,5) (5,2) 7 6 21 0.17 0.58
(3,4) (4,3)
(2,6) (6,2) (3,5) (5,3) 8 5 26 0.14 0.72
(4,4)
(3,6) (6,3) (4,5) (5,4) 9 4 30 0.11 0.83
(4,6) (6,4) (5,5) 10 3 33 0.08 0.92
(5,6) (6,5) 11 2 35 0.06 0.97
(6,6) 12 1 36 0.03 1.00
Total 36

3.2 Histogram

A histogram is a graphical representation of a frequency table. Histograms
also are used to show the shape of a distribution. Some common shapes are
bell-shaped (i.e., normal), exponential or skewed. Skewed distributions are
similar to normal distributions only one tail is significantly larger than the
other. For example, a skewed right distribution has a basic bell-shaped curve
with a longer tail on the right (or on the left). The figure below shows each
of these shapes.

11


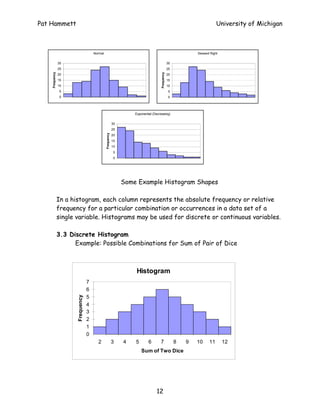
Normal Skewed Right

30 30
25 25
Frequency

Frequency
20 20
15 15
10 10
5 5
0 0

Exponential (Decreasing)

30
25
Frequency

20
15
10
5
0

Some Example Histogram Shapes

In a histogram, each column represents the absolute frequency or relative
frequency for a particular combination or occurrences in a data set of a
single variable. Histograms may be used for discrete or continuous variables.

3.3 Discrete Histogram
Example: Possible Combinations for Sum of Pair of Dice

Histogram
7
6
5
Frequency

4
3
2
1
0
2 3 4 5 6 7 8 9 10 11 12
Sum of Two Dice

12


3.4 Continuous Data Histogram

To demonstrate a continuous data histogram, suppose you obtain the
following data set by measuring the diameter of 100 bicycle seat posts.

25.36 25.34 25.39 25.45 25.37
25.36 25.40 25.35 25.36 25.37
25.40 25.41 25.41 25.35 25.38
25.39 25.39 25.37 25.44 25.42
25.40 25.36 25.37 25.39 25.39
25.40 25.38 25.33 25.36 25.43
25.42 25.41 25.41 25.37 25.40
25.47 25.41 25.32 25.46 25.40
25.39 25.42 25.41 25.42 25.35
25.42 25.41 25.42 25.41 25.46
25.40 25.40 25.43 25.36 25.41
25.44 25.46 25.41 25.37 25.36
25.38 25.50 25.38 25.40 25.40
25.40 25.39 25.36 25.36 25.44
25.38 25.38 25.39 25.40 25.35
25.41 25.34 25.39 25.40 25.34
25.55 25.43 25.42 25.41 25.39
25.40 25.36 25.42 25.41 25.45
25.45 25.39 25.40 25.36 25.41
25.35 25.43 25.40 25.38 25.38

First, arrange the data into frequency or bin ranges of equal width. The
selection of the number and width of the bins (frequency ranges) is
dependent on the analyst. For continuous data, a general rule of thumb is to
set the number of bins equal to the square root of the number of samples
(rounded to nearest whole number). To obtain the bin width, divide the range
of the data set by the number of bins (rounded to desired precision of
measurement data). This example has 100 samples and a range of 0.23. Thus,
an analyst might create 10 bins (=sqrt(100)) of width 0.02 mm (0.23/10 =
0.02). In this example, the value 25.34 was chosen as the starting point
because relatively few values are below it.

13


Absolute Cumulative
Bin Range
Frequency Frequency
< 25.34 3 3
25.34 < X <= 25.36 13 16
25.36 < X <= 25.38 14 30
25.38 < X <= 25.4 24 54
25.40 < X <= 25.42 27 81
25.42 < X <= 25.44 6 87
25.44 < X <= 25.46 9 96
25.46 < X <= 25.48 2 98
25.48 < X <= 25.5 1 99
X > 25.50 1 100

Histogram
30
Frequency

25
20
15
10
5
0
.4

.5

e
4

6

8

2

4

6

8
.3

.3

.3

.4

.4

.4

.4

or
25

25
25

25

25

25

25

25

25

M

Bin

Interpreting a Continuous Data Histogram – the absolute frequencies in a
continuous data histogram represent the number of observations that fall
within a range. In the graph above, the first column (labeled 25.34)
represents the number of observations less than or equal to 25.34. The
second column (labeled 25.36) represents the number of observations
greater than 25.34 and less than or equal to 25.36. The third column is the
number of observations greater than 25.36 and less than or equal to 25.38.

14


4. NORMAL DISTRIBUTION

The Normal distribution, visually resembling a smooth, symmetrical, bell-shaped
curve, represents a commonly found pattern of randomly measured data. It is
used to describe a great variety of situations such as intelligence test results,
part measurements from automatic machines, measurement errors from a gage,
etc. In fact, the failure to find a normal distribution when studying a continuous
process often suggests that some factor is exerting an unusual amount of
influence on the process (special cause of variation exists).

• Understand Some Common Properties of Normal Distribution and the
Standard Normal Distribution.
• Estimate the probability of an event given that the observed data follow
a normal distribution.

4.1 Properties of the Normal Distribution

The figure below shows a normal distribution. In a normal distribution, the
mean, median, and mode all coincide. In addition, the number of standard
deviations about the mean may be represented by probabilities. For example,
if data are normally distributed, then 99.73% of values should fall between
+/- 3σ.

−3σ −2σ −1σ +1σ +2σ +3σ
−1σ −2σ −3σ
+/- 1σ = 68.26%
+/- 2σ = 95.46%
+/- 3σ = 99.73%
Properties of a Normal Distribution

15


4.2 Estimating Probabilities Using Normal Distribution

If data are normally distributed (or reasonably assumed to be normal), event
probabilities may be empirically derived based on parameter estimates. To
use the normal distribution, values are first converted to standardized Z
scores. To standardize data, we use the following transformation:

Z = (X – µ) / σ

Z scores transform data into the standard cumulative normal distribution
whose mean = 0, and variance (σ2) = 1. Z-scores provide a mapping from a
distribution of some variable to a standardized scale. These mappings
reflect the difference in terms of number of standard deviations away from
the mean. If the mean of a process = 4 mm and the standard deviation = 1,
then an observed value of 1 could also be represented as –3*standard
deviation from the mean. For this example, a Z = -3 is equivalent to an actual
observation of 1 (where Z = –3*standard deviation away from the mean).

By standardizing data, the probability of an event may be obtained by using
the Z-scores. For example, suppose you wanted to compute the probability
that a value falls between 4 and 16 given a mean = 10 and a standard
deviation = 2.

Pr (4 < X < 16) = Pr (X < 16) – Pr (X < 4)

Z (X = 4) = (4 – 10) / 2 = -3.0
Z (X = 16) = (16 – 10) / 2 = 3.0

Pr (Z< -3.0) = 0.00135
(See appendix for Standardize Normal Curve Table)

Pr (Z< 3.0) = 0.99865 (or 1 – 0.00135)
(See appendix for Standardize Normal Curve Table)

Pr (Z < 3) – Pr (Z < -3) = 0.99865 – 0.00135 = 0.9973

Thus, 99.73% of values will fall between +/- 3σ.

16


4.3 Calculating Parts Per Million Defects Given Normal Distribution

If data are normally distributed, parts per million defects may be estimated
using the standardized normal curve. The following process provides a step-
by-step process for calculating parts per million defects assuming that the
data follow a normal distribution and the process has a bilateral tolerance.

Step 1: Obtain necessary input data information.
• Specifications: Target, Upper Specification Limit (USL), and the
Lower Specification Limit (LSL).
• Summary Statistics from Data Set: Estimate of the Sample Mean and
Standard Deviation.

Example: Suppose you are trying to bicycle seats whose diameter
specification is 25.4 +/- 0.05. You sample 100 parts and obtain a mean =
25.41 and sample standard deviation = 0.02.

Target = 25.4; USL = 25.45; LSL = 25.35; Mean = 25.41; Std Dev = 0.02

Step 2: Pictorially show the USL, LSL, Target, Mean, and Std Deviation

TIP: identify whether the mean is closer to the USL or the LSL as the
defects per million should be greater on the side that is closest to the mean.

Example: graph of the above problem.

Mean = 25.41

LSL = 24.35 USL = 25.45

Target
25.4

17


Step 3: Calculate the probability of a defect above the USL and below
the LSL.

Pr[Z > Zusl]
Pr[Z < Zlsl]
= 1 - Pr[Z < Zusl)

DEFECT

LSL USL

3a. Calculate Pr(Defect > USL). To obtain the probability that a part will
be greater than the USL, we need to calculate a Z-value for the USL (Zusl)
and look up the probability in a normal probability table. Note: we may also
use an Excel built-in function to obtain this probability.

Compute Zusl = (USL – Mean) / std deviation
From Zusl, we may determine the Pr (Defect > USL).
Pr (Defect > USL) = 1 – Pr(Z<Zusl).

Normal probability tables are presented as the probability from negative
infinity to Z. Thus, for calculating defects greater than the USL, we need to
let Pr (Defect > USL) = 1 – Pr (Z < Zusl). Pr(Z < Zusl) is obtained by looking up
the value for Zusl in a normal probability table.

Example:
Target = 25.4; USL = 25.45; LSL = 25.35;
Mean = 25.41; Std Dev = 0.02

Zusl = (25.45 – 25.41) / 0.02 = 2.00

Pr (Z < Zusl) = 0.97725 (based on Normal Table where Zusl = 2.0)
Alternatively in Excel: =normsdist(2.0) 0.97725

Pr (Defect > USL) = 1 – Pr (Z < Zusl) = 1 – 0.97725 = 0.02275

18


3b. Calculate Pr(Defect < LSL). To obtain the probability that a part will
be less than the LSL, we need to calculate a Z-value for the LSL (Zlsl) and
look up the probability in a normal probability table. Note: we may also use an
Excel built-in function to obtain this probability.

Compute Zlsl = (LSL – Mean) / std deviation
From Zlsl, we may determine the Pr (Defect < LSL).
Pr (Defect < LSL) = Pr(Z< Zlsl).

Normal probability tables are presented as the probability from negative
infinity to Z. Thus, for calculating defects less than the LSL, we need to let
Pr (Defect < LSL) = Pr (Z< Zlsl). Pr(Z < Zlsl) is obtained by looking up the
value for Zlsl in a normal probability table.

Example:
Target = 25.4; USL = 25.45; LSL = 25.35;
Mean = 25.41; Std Dev = 0.02

Zlsl = (25.35 – 25.41) / 0.02 = -3.00

Pr (Z < Zlsl) = 0.00135 (based on Normal Table Lookup where Z = -3.0)
Alternatively in Excel: =normsdist(-3.0) 0.00135

Pr (Defect < LSL) = 0.00135

Step 4: Calculate the probability of a defect.

Pr (Defect) = Pr (Defect > USL) + Pr (Defect < LSL)

Example: Pr (Defect) = 0.02275 + 0.00135 = 0.02410

Step 5: Calculate the Actual DPM

Actual DPM = Pr (Defect) * 1,000,000

Example: Actual DPM = 0.02410 * 1M = 24,100 DPM

19


5. LINEAR REGRESSION ANALYSIS

Regression is used to describe relationships between variables.

• Compute the slope and y-intercept using a simple linear regression.
• Compute and interpret simple correlation coefficient.
• Understand the difference between simple linear regression and multiple
linear regression.


5.1 General Regression equation

The regression equation is used to describe the relationship between the
response variables and predictor(s). The general equation is:

Y = βo + β1X1 + β2 X2 + ... βn Xn

Y – represents the response variable.
βo – represents the Y-intercept (value of response when predictor(s)
variable = 0).
β(1..n) - is the slope or rate of change of each predictor variable.
X(1..n) - is the value of each predictor variable.

5.2 Simple linear regression

Simple linear regression examines the linear relationship between two
variables: one response (y) and one predictor (x). If the two variables are
related, the regression equation may be used to predict a response value
given a predictor value with better than random chance. The simple linear
regression equation is:

Y = βo + β1X1

20


The most common method used to determine the line that “best” fits data is
Least Squares Regression, which minimizes the squared deviations between
individual observations and the regression line.

The equations used to compute the slope (β1) and Y-intercept (βo) are:

n(∑ ( X i Yi )) − (∑ X i )(∑ Yi )
β1 =
( )
n ∑ X i2 − (∑ X i )
2

∑Y − β 1 (∑ X i )
βo =
i

n
Note: n is the number of samples.

Alternatively, you could use the excel functions =slope(Y-array,X-array) and
=intercept(Y-array,X-array). For example, if the Y-variable data are in Excel
work cells B2:B10 and the X-variable data are in cells A2:A10, then the
formula would be =slope(B2:B10,A2:A10).

Simple Linear Regression Example

Suppose you conduct an experiment to examine the relationships between
bicycle tire pressure, tire width, and the coefficient of rolling friction. From
experiments, you obtain the following:

Coefficient of Rolling Friction for Bicycle Tires
Pressure (PSI) Width=1.25" Width= 2"
20 0.0100 0.0107
25 0.0095 0.0100
30 0.0088 0.0093
35 0.0081 0.0086
40 0.0074 0.0079
45 0.0067 0.0073
50 0.0060 0.0071
55 0.0058 0.0068
60 0.0056 0.0066
65 0.0054 0.0063
70 0.0052 0.0061
75 0.0050 0.0058

21


Given these data, estimate the slope and Y-intercept for both variables.

Using excel, the following results may be obtained.

Width=1.25" Width= 2"
slope -0.0001 -0.0001
intercept 0.0115 0.0118

5.3 Correlation

The Pearson correlation coefficient measures the extent to which two
continuous variables are linearly related. For example, you may want to
measure the correlation between tire pressure and the coefficient of rolling
friction in the above example.

Simple correlation may be measured using the following equation:

R=
∑ (x i )(
− x yi − y )
(n − 1)s x s y

Using excel, =correl(Yarray,Xarray)

The correlation coefficient, R, consists of a value between –1 and 1. Perfect
correlation (either –1 or 1) occurs when every observation in a sample falls
exactly on the predicted line (i.e., no error).

Strong positive correlation (value approaching 1) exists when both variables
increase or decrease concurrently. A correlation value, R, which is greater
than 0.7, typically indicates a strong positive relationship.

Strong negative correlation (value approaching –1) exists if one variable
increases while the other variable decreases. A correlation value, R, which is
less than -0.7, typically indicates a strong negative relationship.

22


5.4 Using Scatter Plots to Show Linear Relationships

A scatter plot is an effective tool for viewing the strength (strong – weak
correlation) and direction (positive and negative). The figures below show
several examples with different correlation coefficients.

Response Variable
Response Variable

Predictor Variable Predictor Variable

a) Perfect Positive Correlation (R = 1.0) b) Perfect Negative Correlation (R = -1.0)
Response Variable

Response Variable

Predictor Variable Predictor Variable

c) Strong Positive Correlation (R = 0.7) d) Strong Negative Correlation (R = -0.7)

Note: If two variables are normally distributed with no correlation (i.e.,
R=0), the resulting figure will resemble a circle.

Interpreting Correlation Coefficients

When drawing conclusions based on correlation coefficients, several
important items must be considered:

• Correlation coefficients only measure linear relationships. A
meaningful nonlinear relationship can exist even if the correlation
coefficient is 0.

• Correlation does NOT always indicate cause and effect. One should
not conclude that changes to one variable cause changes in another.
Properly controlled experiments are needed to verify that a
correlation relationship indicates causation.

23


• A correlation coefficient is very sensitive to extreme values. A single
value that is very different from the others in a data set can change
the value of the coefficient a great deal. In the example below, the
correlation is 0.9, but the scatter plot suggests that an outlier more
likely explains the relationship that the predictor variable. If you
removed the outlier value, the correlation between these two variable
would drop to 0.1 over the smaller range of X.

Tonnage Vs. Drawdepth

61.00
60.80
60.60
Drawdepth

60.40
60.20
60.00
59.80
910 920 930 940 950
Tonnage

5.5 Multiple linear regression

Multiple linear regression examines the linear relationships between one
continuous response and two or more predictors. If the response and
predictor variables are related, the regression equation may be used to
predict a response value given predictor values with better than random
chance.

When using multiple linear regression, one should exercise caution if the
number of predictors is large, particularly in relation to the sample size. For
example, trying to fit a multiple regression model with 5 predictor variables
and only 10 data points is likely to yield problems, especially if the predictor
variables are not independent of each other (i.e., no relationship). Here, one
should reference a more advanced regression technique.

24


Appendix A. PRACTICE TEST

In making calculations, feel free to use a calculator or software (Excel or Minitab). The answers
also are available in an appendix. Note: these problems are based on this probability and
statistics review manual.

Descriptive Statistics

Use this information from UM’s 11-game football season to answer the following:

University of Michigan - Football Statistics by Game (Year
2000)

Game UM- Opp- Point UM Opponent
Score Score Difference Offense Offense
1 42 7 35 554 271
2 38 7 31 396 271
3 20 23 -3 374 394
4 35 31 4 513 447
5 13 10 3 375 278
6 31 32 -1 430 530
7 58 0 58 562 190
8 14 0 14 326 355
9 51 54 -3 535 654
10 33 11 22 444 407
11 38 26 12 389 400

N 11 11 11 11 11
Sum 373 201 172 4898 4197
Minimum 13 0 -3 326 190
Maximum 58 54 58 562 654

1. What is the average number offense per game for UM football team?

2. What is the standard deviation of offense per game for UM football team?

3. What is the median point difference (UM Score – Opponent Score)?

25


Normal Distribution

An automotive body manufacturer collects data on the height of their dash panel. They
record all measurements as deviation from nominal (thus, the target value = 0). Based
on a sample of 50 vehicles, they obtain the following information: Mean = 0.30 mm and
Standard Deviation = 0.20 mm. The specification for dash height is 0 +/- 1 mm.

4. What is the probability that a vehicle will have a height above the upper specification limit?

5. Estimate the part per million defects for dash panel height.

6. What percentage of products should fall between +/- 2.0 sigma of the process mean (0.30
mm)?

26


Simple Linear Regression and Correlation Analysis:

Use the following scatter plots to answer the following questions and information from the
Descriptive Statistics Table.

Correlation = 0.42 Correlation = -0.75
70 70
60 60
50 50
Point Difference

Point Difference
40 40
30 30
20 20
10 10
0 0
-10 -10
100 200 300 400 500 600 100 200 300 400 500 600 700
UM Offense Opponent Offense

(UM Offense VS. Point Difference) (Opponent Offense Vs. Point Difference)

7. Which of the following has a strong negative correlation?

a. UM Offense and Point Difference
b. Opponent Offense and Point Difference
c. Both (a) and (b).
d. Neither (a) or (b).

8. Which of the following statements appears true based on the available data?

a. The UM defense (measured by Opponents offense) is a better predictor of point
difference than UM Offense.
b. The UM offense is a better predictor of point difference than UM Defense.
c. Cannot tell based on the information given.

9. What is slope of the best fit line between UM Offense and Point Difference?

10. What is the y-intercept of the best fit line between UM Offense and Point Difference?

27


Answers to Practice Test

1. Mean = 445.3
2. StDev = 82.6
3. Median = 12
4. Pr (X > USL) = Pr [Z > (1-0.3)/0.2] Pr (Z > 3.5) = 0.00023
5. Pr (Z < -6.5) + Pr (Z > 3.5) x 1M = (~0 + 0.00023 ) x 1M = 230 DPM
Note : Zlsl = (-1 – 0.3) / 0.2 = - 6.5.
6. Pr (Z < 2) + Pr (Z < -2) = 0.97725 – 0.02275 = 0.9545 or 95.5%
7. (b) Opponent offense and point difference has strong negative correlation R
8. (a) UM defense has stronger correlation (-0.7) than UM offense (0.4)
9. Slope (X – UM Offense, Y – Point Difference) = 0.098
10. Y-Intercept (X – UM Offense, Y – Point Difference) = -28.102

28


Appendix B: Cumulative Normal Distribution Function (-Z values)
(Some examples: Z = -2.11 = 0.01743; Z = 1.50 = 0.93319)

Z 0.09 0.08 0.07 0.06 0.05 0.04 0.03 0.02 0.01 0.00
-3.5 0.00017 0.00017 0.00018 0.00019 0.00019 0.00020 0.00021 0.00022 0.00022 0.00023
-3.4 0.00024 0.00025 0.00026 0.00027 0.00028 0.00029 0.00030 0.00031 0.00032 0.00034
-3.3 0.00035 0.00036 0.00038 0.00039 0.00040 0.00042 0.00043 0.00045 0.00047 0.00048
-3.2 0.00050 0.00052 0.00054 0.00056 0.00058 0.00060 0.00062 0.00064 0.00066 0.00069
-3.1 0.00071 0.00074 0.00076 0.00079 0.00082 0.00084 0.00087 0.00090 0.00094 0.00097
-3.0 0.00100 0.00104 0.00107 0.00111 0.00114 0.00118 0.00122 0.00126 0.00131 0.00135
-2.9 0.00139 0.00144 0.00149 0.00154 0.00159 0.00164 0.00169 0.00175 0.00181 0.00187
-2.8 0.00193 0.00199 0.00205 0.00212 0.00219 0.00226 0.00233 0.00240 0.00248 0.00256
-2.7 0.00264 0.00272 0.00280 0.00289 0.00298 0.00307 0.00317 0.00326 0.00336 0.00347
-2.6 0.00357 0.00368 0.00379 0.00391 0.00402 0.00415 0.00427 0.00440 0.00453 0.00466
-2.5 0.00480 0.00494 0.00508 0.00523 0.00539 0.00554 0.00570 0.00587 0.00604 0.00621
-2.4 0.00639 0.00657 0.00676 0.00695 0.00714 0.00734 0.00755 0.00776 0.00798 0.00820
-2.3 0.00842 0.00866 0.00889 0.00914 0.00939 0.00964 0.00990 0.01017 0.01044 0.01072
-2.2 0.01101 0.01130 0.01160 0.01191 0.01222 0.01255 0.01287 0.01321 0.01355 0.01390
-2.1 0.01426 0.01463 0.01500 0.01539 0.01578 0.01618 0.01659 0.01700 0.01743 0.01786
-2.0 0.01831 0.01876 0.01923 0.01970 0.02018 0.02068 0.02118 0.02169 0.02222 0.02275
-1.9 0.02330 0.02385 0.02442 0.02500 0.02559 0.02619 0.02680 0.02743 0.02807 0.02872
-1.8 0.02938 0.03005 0.03074 0.03144 0.03216 0.03288 0.03362 0.03438 0.03515 0.03593
-1.7 0.03673 0.03754 0.03836 0.03920 0.04006 0.04093 0.04182 0.04272 0.04363 0.04457
-1.6 0.04551 0.04648 0.04746 0.04846 0.04947 0.05050 0.05155 0.05262 0.05370 0.05480
-1.5 0.05592 0.05705 0.05821 0.05938 0.06057 0.06178 0.06301 0.06426 0.06552 0.06681
-1.4 0.06811 0.06944 0.07078 0.07215 0.07353 0.07493 0.07636 0.07780 0.07927 0.08076
-1.3 0.08226 0.08379 0.08534 0.08692 0.08851 0.09012 0.09176 0.09342 0.09510 0.09680
-1.2 0.09853 0.10027 0.10204 0.10383 0.10565 0.10749 0.10935 0.11123 0.11314 0.11507
-1.1 0.11702 0.11900 0.12100 0.12302 0.12507 0.12714 0.12924 0.13136 0.13350 0.13567
-1.0 0.13786 0.14007 0.14231 0.14457 0.14686 0.14917 0.15151 0.15386 0.15625 0.15866
-0.9 0.16109 0.16354 0.16602 0.16853 0.17106 0.17361 0.17619 0.17879 0.18141 0.18406
-0.8 0.18673 0.18943 0.19215 0.19489 0.19766 0.20045 0.20327 0.20611 0.20897 0.21186
-0.7 0.21476 0.21770 0.22065 0.22363 0.22663 0.22965 0.23270 0.23576 0.23885 0.24196
-0.6 0.24510 0.24825 0.25143 0.25463 0.25785 0.26109 0.26435 0.26763 0.27093 0.27425
-0.5 0.27760 0.28096 0.28434 0.28774 0.29116 0.29460 0.29806 0.30153 0.30503 0.30854
-0.4 0.31207 0.31561 0.31918 0.32276 0.32636 0.32997 0.33360 0.33724 0.34090 0.34458
-0.3 0.34827 0.35197 0.35569 0.35942 0.36317 0.36693 0.37070 0.37448 0.37828 0.38209
-0.2 0.38591 0.38974 0.39358 0.39743 0.40129 0.40517 0.40905 0.41294 0.41683 0.42074
-0.1 0.42465 0.42858 0.43251 0.43644 0.44038 0.44433 0.44828 0.45224 0.45620 0.46017
0.0 0.46414 0.46812 0.47210 0.47608 0.48006 0.48405 0.48803 0.49202 0.49601 0.50000

29


Cumulative Normal Distribution Function (Positive Z-values)

Z 0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09
0.0 0.50000 0.50399 0.50798 0.51197 0.51595 0.51994 0.52392 0.52790 0.53188 0.53586
0.1 0.53983 0.54380 0.54776 0.55172 0.55567 0.55962 0.56356 0.56749 0.57142 0.57535
0.2 0.57926 0.58317 0.58706 0.59095 0.59483 0.59871 0.60257 0.60642 0.61026 0.61409
0.3 0.61791 0.62172 0.62552 0.62930 0.63307 0.63683 0.64058 0.64431 0.64803 0.65173
0.4 0.65542 0.65910 0.66276 0.66640 0.67003 0.67364 0.67724 0.68082 0.68439 0.68793
0.5 0.69146 0.69497 0.69847 0.70194 0.70540 0.70884 0.71226 0.71566 0.71904 0.72240
0.6 0.72575 0.72907 0.73237 0.73565 0.73891 0.74215 0.74537 0.74857 0.75175 0.75490
0.7 0.75804 0.76115 0.76424 0.76730 0.77035 0.77337 0.77637 0.77935 0.78230 0.78524
0.8 0.78814 0.79103 0.79389 0.79673 0.79955 0.80234 0.80511 0.80785 0.81057 0.81327
0.9 0.81594 0.81859 0.82121 0.82381 0.82639 0.82894 0.83147 0.83398 0.83646 0.83891
1.0 0.84134 0.84375 0.84614 0.84849 0.85083 0.85314 0.85543 0.85769 0.85993 0.86214
1.1 0.86433 0.86650 0.86864 0.87076 0.87286 0.87493 0.87698 0.87900 0.88100 0.88298
1.2 0.88493 0.88686 0.88877 0.89065 0.89251 0.89435 0.89617 0.89796 0.89973 0.90147
1.3 0.90320 0.90490 0.90658 0.90824 0.90988 0.91149 0.91308 0.91466 0.91621 0.91774
1.4 0.91924 0.92073 0.92220 0.92364 0.92507 0.92647 0.92785 0.92922 0.93056 0.93189
1.5 0.93319 0.93448 0.93574 0.93699 0.93822 0.93943 0.94062 0.94179 0.94295 0.94408
1.6 0.94520 0.94630 0.94738 0.94845 0.94950 0.95053 0.95154 0.95254 0.95352 0.95449
1.7 0.95543 0.95637 0.95728 0.95818 0.95907 0.95994 0.96080 0.96164 0.96246 0.96327
1.8 0.96407 0.96485 0.96562 0.96638 0.96712 0.96784 0.96856 0.96926 0.96995 0.97062
1.9 0.97128 0.97193 0.97257 0.97320 0.97381 0.97441 0.97500 0.97558 0.97615 0.97670
2.0 0.97725 0.97778 0.97831 0.97882 0.97932 0.97982 0.98030 0.98077 0.98124 0.98169
2.1 0.98214 0.98257 0.98300 0.98341 0.98382 0.98422 0.98461 0.98500 0.98537 0.98574
2.2 0.98610 0.98645 0.98679 0.98713 0.98745 0.98778 0.98809 0.98840 0.98870 0.98899
2.3 0.98928 0.98956 0.98983 0.99010 0.99036 0.99061 0.99086 0.99111 0.99134 0.99158
2.4 0.99180 0.99202 0.99224 0.99245 0.99266 0.99286 0.99305 0.99324 0.99343 0.99361
2.5 0.99379 0.99396 0.99413 0.99430 0.99446 0.99461 0.99477 0.99492 0.99506 0.99520
2.6 0.99534 0.99547 0.99560 0.99573 0.99585 0.99598 0.99609 0.99621 0.99632 0.99643
2.7 0.99653 0.99664 0.99674 0.99683 0.99693 0.99702 0.99711 0.99720 0.99728 0.99736
2.8 0.99744 0.99752 0.99760 0.99767 0.99774 0.99781 0.99788 0.99795 0.99801 0.99807
2.9 0.99813 0.99819 0.99825 0.99831 0.99836 0.99841 0.99846 0.99851 0.99856 0.99861
3.0 0.99865 0.99869 0.99874 0.99878 0.99882 0.99886 0.99889 0.99893 0.99896 0.99900
3.1 0.99903 0.99906 0.99910 0.99913 0.99916 0.99918 0.99921 0.99924 0.99926 0.99929
3.2 0.99931 0.99934 0.99936 0.99938 0.99940 0.99942 0.99944 0.99946 0.99948 0.99950
3.3 0.99952 0.99953 0.99955 0.99957 0.99958 0.99960 0.99961 0.99962 0.99964 0.99965
3.4 0.99966 0.99968 0.99969 0.99970 0.99971 0.99972 0.99973 0.99974 0.99975 0.99976
3.5 0.99977 0.99978 0.99978 0.99979 0.99980 0.99981 0.99981 0.99982 0.99983 0.99983

30


Appendix C: Some Useful excel statistical functions
(Note: an array represents a sample data set in excel)

Count =count(array)
Sum =sum(array)
Mean (average) =average(array)
Median =median(array)
Standard Deviation =stdev(array)
Variance =var(array)
Maximum =max(array)
Minimum =min(array)

Percentile =percentile(array,value)
e.g., to find the 95th percentile =percentile(array,0.95)

Slope =slope(Y array, X array)
Intercept =intercept(Y array, X array)

Correlation =correl(array 1, array 2)

Normal Distribution Function:
=normdist(X,mean,standard deviation, true) returns the Prob(x < X) using the
cumulative normal distribution based on the specified mean and standard
deviation.

=normsdist(Z) returns the Prob(z < Z) using the standard normal cumulative
distribution (mean of zero and standard deviation of one).

=normsinv(probability) returns the inverse of the standard normal cumulative
distribution for a given probability.

Random Number Generator – rand() may be used to generate a random number
between 0 and 1.

31

Introduction to basic statistics

More Related Content

Introduction to basic statistics