Famous problem IMO 1988 Q6.pdf

Boletı́n de la Asociación Matemática Venezolana, Vol. XVIII, No. 2 (2011) 143
Another perspective on a famous problem,
IMO 1988: The equation x2+y2
xy+1 = n2
Luis Gómez Sánchez Alfaro
DIVULGACIÓN MATEMÁTICA
Abstract. In this work we apply a simple property of the function
F below to study an interesting IMO problem proposed in 1988 of
which we give a solution. We analyze with some detail the diophan-
tine equation F(x, y) = n2
in connection with this problem.
Resumen. En este trabajo se aplica una simple propiedad de la
función F, ver abajo, para estudiar un interesante problema pro-
puesto en la OMI de 1988, del cual damos una solución. Se analiza
con cierto detalle la ecuación diofántica F(x, y) = n2
en relación con
este problema.
The symmetrical function F(x, y) = x2
+y2
xy+1 of R+ × R+ in R+ has the re-
markable property, trivial to verify: F(x, x3
) = F(x, 0) = x2
for all x.
Here we use basically this property to determine an infinity of integer so-
lutions of the equation F(x, y) = n2
for all n ≥ 2. We give first a solution,
apparently new, to a famous problem [see (9) below] proposed by Stephan Beck,

144 Luis G. Sánchez Alfaro
Federal Germany, in the 29◦
International Olympic Games of Mathematics held
at Canberra, Australia, in 1988. The statement of this problem implies that if n
is not a perfect square, the equation F(x, y) = n does not have integer solutions.
Let us define the function fn from R+
to R+
by fn(x) = F(n, x), i.e.,
fn(x) = n2
+x2
nx+1 ; x ≥ 0
For n ∈ N we have the following properties which are elementary results:
1. fn(m) = fm(n) and fn(0) = fn(n3
) = n2
.
2. fn is 1 − 1 over x > n3
.
3. fn has a unique minimum at n0 = −1+
√
n4+1
n < n.
4. fn decreases over [0, n0] and increases over x > n0
fn(n0) =
2(
√
1 + n4 − 1)
n2
= m0 < 2 for all n; 1 < m0 < 2; n 6= 1
5. For all x 6= n0 in [0, n3
] there exists a unique
y 6= x such that fn(x) = fn(y); in fact y =
n3
− x
nx + 1
∈ [0, n3
]
Let hn be the function defined by hn(x) = n3
−x
nx+1 ; 0 ≤ x ≤ n3
.
Thus hn(x) = y. Note the function hn is involutive, i.e., hn(hn(x)) = x.
6. If x, fn(x) are nonnegative integers, with 0 ≤ x < n3
then hn(x) is a
nonnegative integer.
Moreover, n0 < x < n3
⇐⇒ 0 < hn(x) < n0
Proof:
n2
+ x2
nx + 1
=
n2
+ [hn(x)]2
nhn(x) + 1
= k ⇒
x + hn(x)
n
= k therefore
hn(x) = kn − x is an integer; it must be positive by definition of hn(x).
7. If 0 ≤ a < b then fa(x) > fb(x) for all x > α where α is the unique
positive root of x3
− abx − (a + b) = 0.
Proof: Consider the difference function
g(x) = fb(x) − fa(x) =
−(b − a)[x3
− abx − (a + b)]
(ax + 1)(bx + 1)
; x ≥ 0.
It is easily seen, using the derivative, that g(x) is decreasing over x ≥ 0
going from g(0) = b2
− a2
to −∞ so the equation g(x) = 0 has a unique
positive root α; consequently fa(x) > fb(x) if x > α.

IMO 1988: The equation x2
+y2
xy+1 = n2
. 145
8. If 0 ≤ a < b then fb(x) = fa(x) = β at a unique point x = α where α is
the positive root of x3
− abx − (a + b) = 0.
Furthermore a + b = αβ.
Proof:
b2
+ x2
bx + 1
=
a2
+ x2
ax + 1
⇒ x3
− abx − (a + b) = 0
On the other side
b2
+ α2
bα + 1
=
a2
+ α2
aα + 1
= β ⇒ a + b = αβ
9. PROBLEM 6 (IMO 1988).- Let a and b positive integers such that
ab + 1 divides a2
+ b2
. Show that a2
+b2
ab+1 is the square of an integer.
SOLUTION: With a < b (a = b would give 1 < k < 2 where a2
+b2
ab+1 = k)
consider the functions fa and fb so, k = fb(a) = fa(b) as in (1).
When k = a2
there is nothing to prove. Suppose fa(b) = k > a2
. There
exists always a real c 6= b > a such that k = a2
+b2
ab+1 = a2
+c2
ac+1 from which,
as in the proof of (6), we have b + c = ak hence c is an integer. On the
other hand, when k > a2
, it is easily seen that −1
a < c < 0. This is a
contradiction and therefore we consider only k < a2
. *
We know, by (3) and (4), that fa(x) is increasing at x = b because b > a >
a0 where a0 is the unique point in which fa takes its minimum. Applying
*This is indeed the proposition (13) given below but stated otherwise.

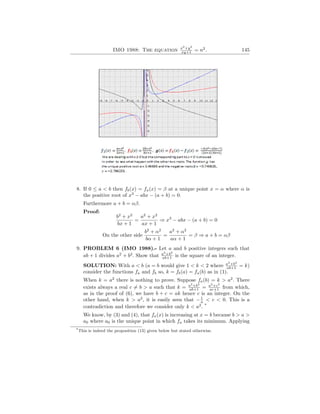
(5) and (6) we obtain the integers k = fa(b) = fa(a1) = fa1 (a) where
0 < a1 = ha(b) < a0 < a < b and obviously a2
> a2
1. Now fa1 (x) is
increasing at x = a which implies 0 < a2 = ha1
(a) < a1 < a0 < a < b and
so on, continuing this way we obtain
k = fan (an+1) = fan+1 (an) = fan+1 (an+2)
where an+2 = han+1
(an)
and b2
> a2
> a2
1 > a2
2 > a2
3 > a2
n > · · · · · · ≥ k
Consequently because of we are dealing with integers, we must have k = a2
n
for a certain index n. The desired result follows.
(*) This indeed the proposition (13) given below but stated otherwise.
NOTE: Paragraph (9) gives a third solution which in addition to the two
previously known to the author, the first given by the Bulgarian partici-
pant in IMO 1988 Emmanuel Atanasiov and the second by the Australian
Professor J. Campbell, University of Canberra (see [1], page 65).
The following figure charts the end of the reasoning used in (9) which
together with (8) and (1) provides a means of finding integer solutions of
the equation x2
+y2
xy+1 = n2
The two curves, fan
and fan−1
are distorted for practical reasons (the real
graphs very quickly stick to the y-axis as can be seen in the figure above
where two real graphs are shown).
As a2
n = fan
(an−1) = fan
(0) = fan
(a3
n) then, by (5), an−1 = a3
n; on the
other hand, (8) gives an + an−2 = a3
nx a2
n = a5
n , i. e., an−2 = a5
n − an
Continuing in the same way we get integers (by ascent, and not, as in (9),
by descent) that are solutions of the proposed equation.

+y2
xy+1 = n2
. 147
SOLUTIONS OF x2
+y2
xy+1 = n2
10. Thus, given fn and the trivial point with integer coordinates (n3
, n2
), we
consider this point as the intersection of fn with another curve fm whose
index m > n, according to (8), is given by n + m = n3
n2
= n5
, i. e.
m = n5
− n (which also goes for the rest solving the equation
f3
n(m) = n2
which gives m =
n5
+
p
(n10 − 4n6 + 4n2
2
= n5
− n).
The iterated application of the procedure gives the recurrence equation
xk+2 = n2
xk+1 − xk, (x0, x1) = (0, n)
whose solutions satisfy the condition fxk
(xk+1) = n2
for all k ≥ 1. The
solutions of this equation are given by
2k
xk =
n[(n2
+ α)k
− (n2
− α)k
])
α
where α =
√
n4 − 4, this is,
2k−1
xk = n
X
i
(k
i )n2(k−i)
αi−1
where the indexes are the positive odds i ≤ k .
We finally have
2k−1
xk = n
[k1]
X
j=0
(k
i )n2(k−2j−1)
(n4
− 4)j

where [k1] denotes the integer part of k1 = k−1
2 and moreover
F(xk, xk+1) =
x2
k + x2
k+1
xkxk+1 + 1
= n2
; k = 1, 2, 3, . . . . . . . . .
11. By construction of the integers xk, the sum in its general definition must be
divisible by 2k−1
which is clear if n is odd and easily verified in each of the
summands if n is even. Therefore each xk is a multiple of n and moreover,
a simple induction using the recurrence equation that defines them proves
that n is the greatest common divisor of each pair of consecutive (xk, xk+1)
in that succession.
12. EXAMPLES:
n = 3 → n3
= 27 → n5
− n = 240 → n7
− 2n3
= 2133 → n9
− 3n5
+ n =
18957 → n11
−4n7
+3n3
= 168480 → n13
−5n9
+6n5
−n = 1497363 →
· · ·
32
= 9 = 32
+272
3∗27+1 = 272
+2402
27∗240+1 = 2402
+21332
240∗2133+1 = 21332
+189572
2133∗18957+1 =
= 189572
+1684802
18957∗168480+1 = 1684002
+14973632
168480∗1497363+1 = · · ·
13. fn(x) is not an integer for all integer x > n3
.
Proof: Suppose x is an integer with x > n3
. If fn(x) is an integer, by
(9) it must be the square of an integer clearly greater than n, then for
some integer h ≥ 1 we have fn(x) = (n + h)2
which gives the equation
n2
+ x2
= (nx + 1)(n + h)2
whose discriminant, n2
(n + h)4
+ 4(2nh + h2
),
should be a perfect square. Then there exists an integer k ≥ 1 such that
2n(n + h)2
k + k2
= 4(2nh + h2
)
i.e. 2kn3
+ k2
+ (kn − 2)(4nh + 2h2
) = 0
This is clearly impossible if (kn − 2) ≥ 0 and then kn = 1, but then we
have 2h2
+ 4h − 3 = 0 which gives h irrational. This completes the proof.
Let [|n|] denotes the infinite set of solutions, generated by n, of the recu-
rrence equation xk+2 = n2
xk+1 − xk, (x0, x1) = (0, n) solved in (10).
14. If fn(x) = b2
; b ∈ N; x ∈ N; 0 < x < n3
, then n ∈ [|b|], i.e. n is one of the
solutions in (10) generated by b.
Proof: Suppose a ∈ N; 0 < a < n3
and fn(a) ∈ N. By (10) we have
fn(a) = m2
< n2
. By the involutive function of (5) we can choose a such
that fn be decreasing in a which means 0 < a < n0 (by (3), (5) and
(6)). Then there exists, by (7) and (8), a function fm increasing in a such
that fm(a) = fn(a) = k2
; k2
< m2
< n2
and moreover m = ak2
− n

+y2
xy+1 = n2
. 149
(Note that n, a and m satisfy the recurrence equation of (10) for the
coefficient k2
). We repeat the procedure, now with fm applied to the
point hm(a) making a descent, as in (9), which should end with fb such
that fb(0) = fb(b3
) = k2
= b2
and then n ∈ [|b|].
15. Theorem.- If p > 0 is a prime number, then the unique integer solutions
(x, z) of the equation fp(x) = z are the trivial ones (0, p2
) and (p3
, p2
).
Proof: It is a consequence of (11), (13) and (14).
CONCLUSION.- Let us denote A = {m ∈ N; m > n3
}. So far we have
obtained the following:
I fn(A) ∩ N = ∅ for all natural n J
I fp(N) ∩ N = {p2
} for all prime p > 0 J
more generally, by (14), we can deduce without difficulty
I fn(N)∩N = {n2
} for all n which does not belong to [|b|] for any non trivial divisor b of n J
We know fn(N) ∩ N trivially contains {n2
}. The discussion above leads to
conjecture it contains at most one non trivial element.
ICONJECTUREJ
For all n > 0, fn(N) ∩ N = {n2
} or {n2
, b2
}; (b < n and, by (14), n ∈ [|b|]
therefore, by (11), b divides n).
Referencias
[1] Francisco Bellot Rosado, Ascensión López Ch. Cien Problemas de Mate-
máticas. ICE, Valladolid, 1994

FOUR VIEWS OF THE SURFACE OF EQUATION z = x2
+y2
xy+1

+y2
xy+1 = n2
. 151
Luis Gómez Sánchez Alfaro
Universidad de Oriente, Venezuela.
e-mail: lagsa7@gmail.com

Famous problem IMO 1988 Q6.pdf

Famous problem IMO 1988 Q6.pdf

More Related Content

Famous problem IMO 1988 Q6.pdf