Design of column base plates anchor bolt

DESIGN OF COLUMN BASE
PLATES AND STEEL
ANCHORAGE TO
CONCRETE
Khaled Eid

Outline
 Introduction
 Base plates
Material
Design using AISC Steel Design Guide
 Concentric axial load
 Axial load plus moment
 Axial load plus shear
 Anchor Rods
Types and Materials
Design using ACI Appendix D
 Tension
 Shear

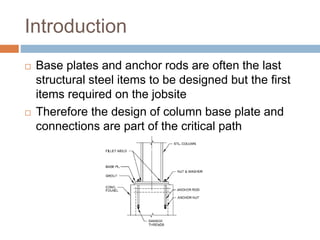
Introduction
 Base plates and anchor rods are often the last
structural steel items to be designed but the first
items required on the jobsite
 Therefore the design of column base plate and
connections are part of the critical path

Introduction
 Anchors to appear in concrete drawings with
location of each anchor in x and y direction
 Pedestal should be designed to suit the
supporting column and anchors
 Usually allow for enough edge distance of 6d
bolt
 Usually use to nuts to avoid slip

Introduction
 Vast majority of column base plate connections
are designed for axial compression with little or no
uplift
 Column base plate connections can also transmit
uplift forces and shear forces through:
 Anchor rods
 Bearing end plate
 Shear lugs under the base plate or embedding the
column base to transfer the shear force.
 Column base plate connections can also be used
to resist wind and seismic loads
 Development of force couple between bearing on
concrete and tension in some or all of the anchor rods

Introduction
 Anchor rods are needed for all base plates to
prevent column from overturning during
construction and in some cases to resist uplift or
large moments
 Anchor rods are designed for pullout and breakout
strength using ACI 318 Appendix D
 Critical to provide well-defined, adequate load
path when tension and shear loading will be
transferred through anchor rods
 In seismic zones the pedestal should carry 2.5 the
factored design load

Introduction
 Grout is needed to adjust the level
 Grout to transfer the load from steel plate to
foundation
 Grout should have design compressive strength at
least twice the strength of foundation concrete
 When base plates become larger than 600mm, it
is recommended that one or two grout holes be
provided to allow the grout to flow easier

Base plate Materials
 Base plates should be ASTM A36 material unless
other grade is available
 Most base plates are designed as to match the
pedestal shape
 A thicker base plate is more economical than a
thinner base plate with additional stiffeners or
other reinforcements

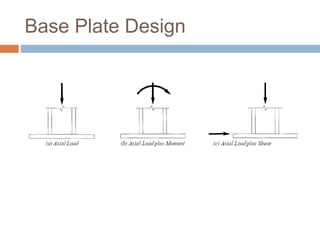
Design of Axially Loaded Base
Plates
 Required plate area is based on uniform allowable
bearing stress. For axially loaded base plates, the
bearing stress under the base plate is uniform
`
A
` 2
f   f 
max 0.85 1.7 p c c c f
A
1
A2 = dimensions of concrete supporting foundation
A1 = dimensions of base plate
 Most economical plate occurs when ratio of concrete
to plate area is equal to or greater than 4 (Case 1)
 When the plate dimensions are known it is not
possible to calculate bearing pressure directly and
therefore different procedure is used (Case 2)

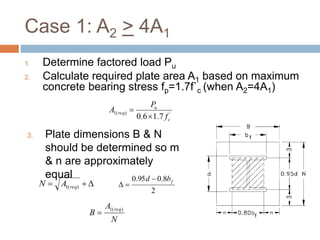
Case 1: A2 > 4A1
1. Determine factored load Pu
2. Calculate required plate area A1 based on maximum
concrete bearing stress fp=1.7f`c (when A2=4A1)
P
u
req f
A
1( ) 0.6 
1.7 ` c

3. Plate dimensions B & N
should be determined so m
& n are approximately
equal
  1(req) N A
0.95 0.8 f d  b
2
 
N
A
B 1(req) 

Case 1: A2 > 4A1
4. Calculate required base plate thickness
N 0.95d
2

0.8 f B b
P
u
2
where l is maximum of m and n
m

5. Determine pedestal area, A2
2
n


F BN
t l
y
0.90
min 
A 4BN 2 

Case 2: Pedestal dimensions
known
1.Determine factored load Pu
2.The area of the plate should be equal to larger
of:
2
A `
1 0.6 1.7 ` c
1

1 0.60 0.85
2





c
u
f
P
A
u
f
P
A


3. Same as Case 1
4. Same as Case 1

Design of Base Plates with
Moments
 Equivalent eccentricity, e, is calculated equal to moment
M divided by axial force P
 Moment and axial force replaced by equivalent axial
force at a distance e from center of column
 Small eccentricities  equivalent axial force resisted by
bearing only
 Large eccentricities necessary to use an anchor bolt
to resist equivalent axial force

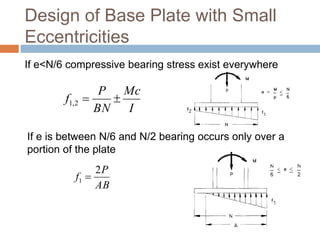
Design of Base Plate with Small
Eccentricities
If e<N/6 compressive bearing stress exist everywhere
Mc
P
f   1,2
If e is between N/6 and N/2 bearing occurs only over a
portion of the plate
P
AB
f
2
1 
I
BN

Design of Base Plate with Small
Eccentricities
1. Calculate factored load (Pu) and moment (Mu)
2. Determine maximum bearing pressure, fp
A
` 2 0.85 1.7 p c c c f
f   f 
A
3. Pick a trial base plate size, B and N
4. Determine equivalent eccentricity, e, and maximum
bearing stress from load, f1. If f1 < fp go to next step,
if not pick different base plate size
5. Determine plate thickness, tp
plu
4
1. Mplu is moment for 1 in wide strip
p F
y
M
t
0.90

`
1

Design of Base Plate with
Shear
 Four principal ways of transferring shear from column
base plate into concrete
1. Friction between base plate and the grout or
concrete surface
n u c c V P f A `  m  0.2
The friction coefficient (m) is 0.55 for steel on grout
and 0.7 for steel on concrete
2. Embedding column in foundation
3. Use of shear lugs
4. Shear in the anchor rods (revisited later in lecture)

Design of Shear Lugs
1. Determine the portion of shear which will be resisted by
shear lug, Vlgu
2. Determine required bearing area of shear lug
u
f
V
A

lg 0.85 c
`
lg

3. Determine shear lug width, W, and height, H
4. Determine factored cantilevered end moment, Mlgu




H G
 
 





M u
 

2
V
lg
lg
W
u
5. Determine shear lug thickness
4 lg
u
F
y
M
t
0.90
lg 

Anchor Rods
 Two categories
 Cast-in place: set before the concrete is placed
 Drilled-in anchors: set after the concrete is hardened

Anchor Rod Materials
 Preferred specification is ASTM F1554
 Grade 36, 55, 105 ksi
 ASTM F1554 allows anchor rods to be supplied
straight (threaded with nut for anchorage) , bent or
headed
 Wherever possible use ¾-in diameter ASTM F1554
Grade 36
 When more strength required, increase rod
diameter to 2 in before switching to higher grade
 Minimum embedment is 12 times diameter of bolt

Cast-in Place Anchor Rods
 When rods with threads and nut are used, a more
positive anchorage is formed
 Failure mechanism is the pull out of a cone of
concrete radiating outward from the head of the bolt
or nut
 Use of plate washer does not add any increased
resistance to pull out
 Hooked bars have a very limited
pullout strength compared with that of
headed rods or threaded rods with
a nut of anchorage

Anchor Rod Placement
 Most common field problem is placement of anchor
rods
 Important to provide as large as hole as possible to
accommodate setting tolerances
 Fewer problems if the structural steel detailer issued
anchor bolt layout for placing the anchors form his 3d
model

Anchor Rod Layout
 Should use a symmetrical pattern in both
directions wherever possible
 Should provide ample clearance distance for
the washer from the column
 Edge distance plays important role for
concrete breakout strength
 Should be coordinated with reinforcing steel to
ensure there are no interferences, more critical
in concrete piers and walls

Design of Anchor Rods for
Tension
 When base plates are subject to uplift force Tu,
embedment of anchor rods must be checked for
tension
 Steel strength of N anchor  A f
in tension
s se ut Ase =effective cross sectional area of anchor, AISC Steel Manual Table 7-18
fut= tensile strength of anchor, not greater than 1.9fy or 125 ksi
 Concrete breakout strength of single anchor in
A
tension
N  N
 
N
cb 2 3 b N  k f ` h
1.5
b c ef No
A
hef=embedment
k=24 for cast-in place anchors, 17 for post-installed anchors
2, 3 = modification factors

Tension
 ANo=Projected area of the
failure surface of a single
anchor remote from edges
 AN=Approximated as the base
of the rectilinear geometrical
figure that results from
projecting the failure surface
outward 1.5hef from the
centerlines of the anchor
Example of calculation of AN with edge
distance (c1) less than 1.5hef
2 No 9 ef A  h
( 1.5 )(2 1.5 ) N 1 ef ef A  c  h  h

Tension
 Pullout strength of anchor
`
pn 4 brg8 c N  A f
 Nominal strength in tension Nn = min(Ns, Ncb,
Npn)
 Compare uplift from column, Tu, to Nn
 If Tu less than Nn ok
 If Tu greater than Nn must provide tension
reinforcing around anchor rods or increase
embedment of anchor rods

Shear
 When base plates are subject to shear force, Vu, and
friction between base plate and concrete is inadequate
to resist shear, anchor rods may take shear
 Steel Strength of single anchor in shear
s se ut V  A f
 Concrete breakout strength of single anchor in shear
A
0.2
l


V  v
  V
1.5
cb 6 7 b
A
vo
b  
 
V o c
7 d f c
1
`
d
o



6, 7 = modification factors
do = rod diameter, in
l = load bearing length of anchor for shear not to exceed 8do, in

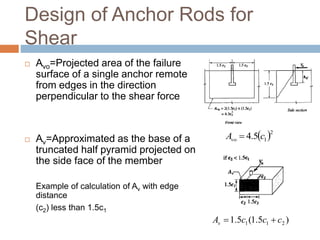
Shear
 Avo=Projected area of the failure
surface of a single anchor remote
from edges in the direction
perpendicular to the shear force
 Av=Approximated as the base of a
truncated half pyramid projected on
the side face of the member
Example of calculation of Av with edge
distance
(c2) less than 1.5c1
 2
A 4.5 c1 vo 
1.5 (1.5 ) 1 1 2 A c c c v  

Shear
 Pryout strength of anchor
cp cp cb V  k N
 Nominal strength in shear Vn = min(Vs, Vcb,
Vcp)
 Compare shear from column, Vu, to Vn
 If Vu less than Vn ok
 If Vu greater than Vn must provide shear
reinforcing around anchor rods or use shear
lugs

Combined Tension and Shear
 According to ACI 318 Appendix D, anchor rods must
be checked for interaction of tensile and shear forces
T
 
V
u
 1.2
n
n
u
V
N

References
 American Concrete Institute (ACI) 318-02
 AISC Steel Design Guide, Column Base Plates, by John T. DeWolf,
1990
 AISC Steel Design Guide (2nd Edition) Base Plate and Anchor Rod
Design
 AISC Engineering Journal Anchorage of Steel Building Components
to Concrete, by M. Lee Marsh and Edwin G. Burdette, First Quarter
1985

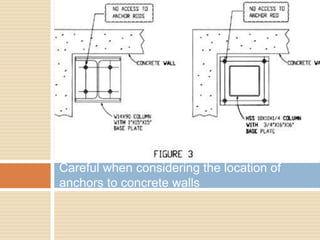
Careful when considering the location of
anchors to concrete walls

Bolts miss alignment or clash with gusset
plate

Design of column base plates anchor bolt

More Related Content

Design of column base plates anchor bolt