Sets in Maths (Complete Topic)

Collection
or Group
What is common in all of
them ?

Collection
or Group
of :
Boys in your Class
Girls in your Class
Vowels in English Alphabet
The rivers of India
Odd numbers
Even numbers

TYPE OF COLLECTION
Not well defined
 Top 3 actors of India
 Top 3 Punjabi Singers
 Top 3 Hindi Songs
Well Defined
 All Vowels in English Alphabet
 Name of all days in a week
 Name of all Months in a year
Note: In Well defined collection, we can definitely decide whether a
given object belongs to the collection or not.

Set: Well
Defined
Collection
of objects
Vowels in English Alphabet
The rivers of India
Odd numbers
Even numbers
Name of days in a week
Names of Months in a year

Things to Remember
Objects, elements and members of a set are
synonymous terms
Sets are usually denoted by Capital Letters like
A,B,C,D,E etc.
The elements of a set are represented by small
letters like a,b,c,d,e etc

Commonly
used Sets in
Maths
• 𝐍 : the set of all natural
numbers
• 𝐙 : the set of all integers
• 𝐐 : Set of all rational
numbers
• 𝐑 : Set of real numbers
• 𝒁+
: Set of positive
integers
• 𝒁−: Set of negative
integers

Notation
• A: set of odd numbers
• 3 is a member of set A.
• 2 is not a member of set A.
• A: set of odd numbers
• 3 ∈ A
• 2 ∉ A
• B: set of vowels in English
Alphabet
• ‘a’ is a member of set B.
• ‘d’ is not a member of set B.
• B: set of vowels in English
Alphabet
• a ∈ A
• b ∉ A
∈ → is a member of (Belongs to)
∉ → is not a member of (does not Belong to)

W A Y S O F R E P R E S E N T I N G A S E T
Roaster/Tabular form
 List all elements of a set.
 A is set of natural numbers less than
10
 is → = set of → {}
 A = {1, 2, 3, 4, 5, 6, 7, 8, 9}
 {} → Braces , → Comma
 List elements using ellipsis.
 A = {1, 2, 3,…,9}
 … → Ellipsis
Set builder form
 Based on common property between
all elements of a set.
 A is set of natural numbers less than
10
 A = {1, 2, 3, 4, 5, 6, 7, 8, 9}
 A = {𝑥 : 𝑥 is natural number and less
than 10}
 A = {𝑥 : 𝑥 <10 and 𝑥 ∈ N}
 where N is a Set of natural numbers
and : → such that

E X A M P L E S
Roaster/Tabular form
 A = {2, 3, 5, 7}
 B = {R, O, Y, A, L}
 C = {-2, -1, 0, 1, 2}
 D {L, O, Y, A}
Order/Arrangement of
elements is not specific here.
Set builder form
 A = {𝑥: 𝑥 is a prime number
less than 10}
 B = {𝑥: 𝑥 is a letter in the
word “ROYAL”}
 C = {𝑥: 𝑥 is an integer and
− 3 < 𝑥 < 3}
 D = {𝑥: 𝑥 is a letter in the
word “LOYAL”}
Note: In Roaster/Tabular Form, repetition is generally not allowed.

Empty
Set
• If a set doesn’t have any
element, it is known as an empty
set or null set or void set. This
set is represented by ϕ or {}.
Example:
• A : Set of prime numbers
between 24 and 28
• B : Set of even prime numbers
greater than 2
• C = { }
• D = {𝑥: 𝑥 is natural number less
than 1}

Singleton Set
• If a set contains only one
element, then it is called a
singleton set.
Example:
between 8 and 12
• B : Set of even prime numbers
• C = {1}
• D = {𝑥: 𝑥 is natural number
less than 2}

Finite Set
If a set contains no element or fixed
number of elements, it is called a finite set.
Example:
A : Set of months in a year
B : Set of prime numbers less than 10
C = {1, 2, 3, 4, 5}
D = {𝑥: 𝑥 is natural number less than 6}

Infinite
Set
• If a set contains endless number
of elements, then it is called an
infinite set.
Example:
• B : Set of even numbers
• C = {1,3,5,7,…}
• D = {𝑥: 𝑥 is a negative integer}

Cardinal
Number
of a Set
• The cardinal number of a finite set
A is the number of distinct
members of the set.
• It is denoted by n(A).
• The cardinal number of the empty
set is 0.
• cardinal number of an infinite set is
not defined.
Example:
• If A= {-3, -2, -1, 0, 1} then n(A) = 5
• If B : Set of months in a year, then
n(B) = 12

Equivalent
Sets
• Two finite sets with an equal
number of members are called
equivalent sets.
• If the sets A and B are equivalent,
we write A ↔ B and read this as
• “A is equivalent to B”.
• A ↔ B if n(A) = n(B) .
Example:
• X= {0, 2, 4}
• Y= {x : x is a letter of the word
DOOR} .
• As n(X) = 3 and n(Y) = 3. So, X ↔ Y .

Equal
Sets
• If two sets contain exactly same
elements, then sets are known as
Equal sets.
Example:
• A : {𝑥: 𝑥 is a vowel in word “loyal”}
• B : {𝑥: 𝑥 is a vowel in word “oral”}
• A = B
• C : Set of positive integers
• D : Set of natural numbers
• C = D

Non-
Equal
Sets
• If two sets do not contain exactly
same elements, then sets are
known as Non-Equal sets.
Example:
• A : {𝑥: 𝑥 is a vowel in word “loyal”}
• B : {𝑥: 𝑥 is a vowel in word “towel”}
• A ≠ B
• C : Set of negative integers
• D : Set of natural numbers
• C ≠ D

Subset and Superset
• If every element of set A is also an element of set B, then A is
called as subset of B or B is superset of A.
• It is denoted as A ⊆ B (subset) or B ⊇ A (superset)
Example:
A : set of vowels in English alphabet
B : set of letters in English alphabet
A ⊆ B or B ⊇ A
C = {1, 2, 3, 4, 5} D = {2, 3}
D ⊆ C or C ⊇ D

Proper Subset and Proper Superset
• If A is a subset of B and A ≠ B, then A is proper
subset of B
• If B is a superset of A and A ≠ B, then B is proper
superset of A
• It is denoted as A ⊂ B (subset) or B ⊃ A (superset)
Example:
C = {1, 2, 3, 4, 5} D = {2, 3}
D ⊂ C or C ⊃ D

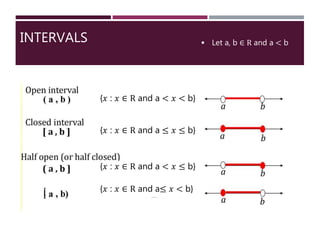
INTERVALS  Let a, b ∈ R and a < b
[
{𝑥 : 𝑥 ∈ R and a < 𝑥 < b}
{𝑥 : 𝑥 ∈ R and a ≤ 𝑥 ≤ b}
{𝑥 : 𝑥 ∈ R and a < 𝑥 ≤ b}
{𝑥 : 𝑥 ∈ R and a≤ 𝑥 < b}

Power Set
The power set is a set which includes all the subsets including the
empty set and the original set itself.
Example:
Let us say Set A = { a, b, c }
Number of elements: 3
Therefore, the subsets of the set are:
Power set of A will be
P(A) = { { } , { a }, { b }, { c }, { a, b }, { b, c }, { c, a }, { a, b, c } }
{ } empty set
{ a }
{ b }
{ c }
{ a, b }
{ b, c }
{ c, a }
{ a, b, c }
The number of elements of a
power set is written as |A|,
If A has ‘n’ elements then it
can be written as
|P(A)| = 2n

Universal Set
• A Universal Set is the set of all elements
under consideration, denoted by U. All
other sets are subsets of the universal set.
• Example:
• A : set of equilateral triangles
• B : set of scalene triangles
• C : set of isosceles triangles
• U : set of triangles (Universal set)
• A ⊂ U, B ⊂ U, C ⊂ U

VENN DIAGRAM
 A Venn diagram used to represent all possible relations of
different sets. It can be represented by any closed figure, whether
it be a Circle or a Polygon (square, hexagon, etc.). But usually, we
use circles to represent each set.
 Example:
 U = {1,2,3,4,5,6,,8,9,10}
 A = {2,4,6,8,10}
Intersecting sets Non Intersecting sets Subsets

Operation on sets
Operations on numbers:
Addition(+) Subtraction(−)
Multiplication(×) Division(÷)
Set operations are the operations that are applied on two more sets to
develop a relationship between them.
There are four main kinds of set operations which are:
 Union of sets
 Intersection of sets
 Complement of a set
 Difference between sets

Union
Notation: A ∪ B
Examples:
{1, 2} ∪ {1, 2} = {1, 2}
{1, 2, 3} ∪ {4, 5, 6} = {1, 2, 3, 4, 5, 6}
{1, 2, 3} ∪ {3, 4} = {1, 2, 3, 4}
The union of sets A and B is
the set of items that are in
either A or B.

Properties of Union of Sets
Commutative Law: The union of two or more sets follows the
commutative law i.e., if we have two sets A and B then,
A ∪ B = B ∪ A
Example: A = {a, b} and B = {b, c, d}
So, A ∪ B = {a,b,c,d}
B ∪ A = {b,c,d,a}
A ∪ B = B ∪ A
Hence, Commutative law proved.

Associative Law: The union operation follows the associative law i.e., if
we have three sets A, B and C then
(A ∪ B) ∪ C = A ∪ (B ∪ C)
Example: A = {a, b} and B = {b, c, d} and C = {a,c,e}
(A ∪ B) ∪ C = {a,b,c,d} ∪ {a,c,e} = {a,b,c,d,e}
A ∪ (B ∪ C) = {a, b} ∪ {b,c,d,e} = {a,b,c,d,e}
Hence, Associative law proved.

Identity Law: The union of an empty set with any set A gives the set itself.
A ∪ ϕ = A
Example: A = {a,b,c} and ϕ = {}
A ∪ ϕ = {a,b,c} ∪ {}
= {a,b,c}
= A
Hence, Identity law proved.

Idempotent Law: The union of any set A with itself gives the set A.
A ∪ A = A
Example: A = {1,2,3,4,5}
A ∪ A = {1,2,3,4,5} ∪ {1,2,3,4,5}
= {1,2,3,4,5} = A
Hence, Idempotent Law proved.

Law of 𝐔 : The union of a universal set U with its subset A gives the
universal set itself.
A ∪ U = U
Example: A = {1,2,4,7} and U = {1,2,3,4,5,6,7}
A ∪ U = {1,2,4,7} ∪ {1,2,3,4,5,6,7}
= {1,2,3,4,5,6,7} = U
Hence, Law of U proved.

Intersection
Notation: A ∩ B
Examples:
{1, 2, 3} ∩ {3, 4} = {3}
{1, 2, 3} ∩ {4, 5, 6} = ϕ or {}
{1, 2} ∩ {1, 2} = {1, 2}
The intersection of sets A
and B is the set of items that
are in both A and B.

Properties of Intersection of Sets
Commutative Law: The union of two or more sets follows the
commutative law i.e., if we have two sets A and B then,
A ∩ B = B ∩ A
Example: A = {a, b} and B = {b, c, d}
So, A ∩ B = {b}
B ∩ A = {b}
So, A ∩ B = B ∩ A
Hence, Commutative law proved.

Associative Law: The union operation follows the associative law i.e., if
we have three sets A, B and C then
(A ∩ B) ∩ C = A ∩ (B ∩ C)
Example: A = {a, b, c} and B = {b, c, d} and C = {a, c, e}
(A ∩ B) ∩ C = {b, c} ∩ {a, c, e} = {c}
A ∩ (B ∩ C) = {a, b, c} ∩ {c} = {c}
Hence, Associative law proved.

Idempotent Law: The union of any set A with itself gives the set A.
A ∩ A = A
Example: A = {1,2,3,4,5}
A ∩ A = {1,2,3,4,5} ∩ {1,2,3,4,5}
= {1,2,3,4,5} = A
Hence, Idempotent law proved.

Law of 𝐔 : The union of a universal set U with its subset A gives the
universal set itself.
A ∩ U = A
A = {1,2,4,7} and U = {1,2,3,4,5,6,7}
Example:
A ∩ U = {1,2,4,7} ∩ {1,2,3,4,5,6,7}
= {1,2,4,7} = A
Hence, Law of U proved.

Difference
Notation: A − B
Examples:
{1, 2, 3} – {2, 3, 4} = {1}
{1, 2} – {1, 2} = 𝜙
{1, 2, 3} – {4, 5} = {1, 2, 3}
The difference of sets A and
B is the set of items that are
in A but not B.

Complement
Notation: A’ or Ac
Examples:
• If U = {1, 2, 3} and A = {1, 2} then Ac = {3}
• If U = {1, 2, 3, 4, 5, 6} and A = {1, 2} then Ac = {3, 4, 5, 6}
The complement of set A is
the set of items that are in
the universal set U but are
not in A.

Properties of
Complement
Sets
Complement Laws:
• A ∪ A’ = U
• A ∩ A’ = 𝜙
For Example:
• If U = {1 , 2 , 3 , 4 , 5 } and A
= {1 , 2 , 3 } then
• A’ = {4 , 5}
• A ∪ A’ = { 1 , 2 , 3 , 4 , 5} = U
• A ∩ A’ = {} = 𝜙

Properties of
Complement
Sets
Law of Double
Complementation:
• (A’)’ = A
For Example:
• If U = {1 , 2 , 3 , 4 , 5 }
and A = {1 , 2 , 3 } then
• A’ = {4 , 5}
• (A’)’ = {1 , 2 , 3} = A
• (A’)’ = A

Properties of
Complement
Sets
Law of empty set and
universal set:
• 𝜙’ = U
• U’ = 𝜙

DE MORGAN’S LAW
The complement of the union of two sets A and B is equal
to the intersection of the complement of the sets A and B.
(A ∪ B)’ = A’ ∩ B’

INCLUSION EXCLUSION PRINCIPLE
n(A U B) = n(A) + n(B) – n(A ∩ B)
 n(A) = 5
 n(B) = 6
 n(A ∩ B) = 2
 n(A U B) = 9

Sets in Maths (Complete Topic)

Sets in Maths (Complete Topic)

More Related Content

Sets in Maths (Complete Topic)